LeetCode 格雷编码问题
格雷编码
- 格雷编码的定义
- 格雷编码的码表
- LeetCode 89. 格雷编码
- 实例
- 思路与代码
- 思路一:找规律
- 代码一
- 代码二
- 思路二:与自然数之间的关系(你必须知道,这个规律要去百度才知道)
- 代码一
- LeetCode 1238. 循环码排列
- 实例
- 思路与代码
- 思路一:找规律
- 代码一
- 思路二:与自然数之间的关系
- 代码一:
格雷编码的定义
格雷编码我们在大学时期已经了解过了,在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。 [2] 在数字系统中,常要求代码按一定顺序变化。例如,按自然数递增计数,若采用8421码,则数0111变到1000时四位均要变化,而在实际电路中,4位的变化不可能绝对同时发生,则计数中可能出现短暂的其它代码(1100、1111等)。在特定情况下可能导致电路状态错误或输入错误。使用格雷码可以避免这种错误。格雷码有多种编码形式。
格雷码(Gray code)曾用过Grey Code、葛莱码、葛兰码、格莱码、戈莱码、循环码、二进制反射码、最小差错码等名字,它们有的是错误的,有的易与其它名称混淆,建议不再使用它们。
格雷编码的码表
| 自然数 | 自然数的二进制 | 一位格雷码 | 二位格雷码 | 三位格雷码 | 四位格雷码 |
|---|---|---|---|---|---|
| 0 | 0000 | 0 | 00 | 000 | 0000 |
| 1 | 0001 | 1 | 01 | 001 | 0001 |
| 2 | 0010 | 11 | 011 | 0011 | |
| 3 | 0011 | 10 | 010 | 0010 | |
| 4 | 0100 | 110 | 0110 | ||
| 5 | 0101 | 111 | 0111 | ||
| 6 | 0110 | 101 | 0101 | ||
| 7 | 0111 | 100 | 0100 | ||
| 8 | 1000 | 1100 | |||
| 9 | 1001 | 1101 | |||
| 10 | 1010 | 1111 | |||
| 11 | 1011 | 1110 | |||
| 12 | 1100 | 1010 | |||
| 13 | 1101 | 1011 | |||
| 14 | 1110 | 1001 | |||
| 15 | 1111 | 1000 |
LeetCode 89. 格雷编码
LeetCode 89. 格雷编码
n 位格雷码序列 是一个由 2n 个整数组成的序列,其中:
每个整数都在范围 [0, 2n - 1] 内(含 0 和 2n - 1)
第一个整数是 0
一个整数在序列中出现 不超过一次
每对 相邻 整数的二进制表示 恰好一位不同 ,且
第一个 和 最后一个 整数的二进制表示 恰好一位不同
给你一个整数 n ,返回任一有效的 n 位格雷码序列 。
实例
输入:n = 2
输出:[0,1,3,2]
解释:
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。
- 00 和 01 有一位不同
- 01 和 11 有一位不同
- 11 和 10 有一位不同
- 10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列,其二进制表示是 [00,10,11,01] 。
- 00 和 10 有一位不同
- 10 和 11 有一位不同
- 11 和 01 有一位不同
- 01 和 00 有一位不同
思路与代码
思路一:找规律
观察格雷码的规律,具有一定的对称性,高位是 1 或者 0,并由此就行对称
代码一
//耗时 6ms
class Solution {public List<Integer> grayCode(int n) {int count = 1;List<Integer> res = new ArrayList<>();res.add(0);res.add(1);while (n-- > 1) {count <<= 1;for (int i = count - 1; i >= 0; i--) {res.add(res.get(i) + count);}}return res;}
}
因为res.get(i)是循环方式去取值,当n的位数确定后格雷数就已经知道多少了,故可以这样写
代码二
class Solution {public List<Integer> grayCode(int n) {Integer[] res = new Integer[1 << n];res[0] = 0;res[1] = 1;int count = 1;while (n-- > 1) {count <<= 1;for (int i = 0; i < count; i++) {res[i + count] = count + res[count - i - 1];}}return Arrays.asList(res);}
}
思路二:与自然数之间的关系(你必须知道,这个规律要去百度才知道)
格雷码→二进制码(解码):
从左边第二位起,将每位与左边一位解码后的值异或,作为该位解码后的值(最左边一位依然不变)。依次异或,直到最低位。依次异或转换后的值(二进制数)就是格雷码转换后二进制码的值。
代码一
class Solution {public List<Integer> grayCode(int n) {List<Integer> res = new ArrayList<>();int sum = 1<<n;for(int i = 0;i < sum;i++){res.add((i >> 1) ^ i);}return res;}
}
LeetCode 1238. 循环码排列
LeetCode 1238. 循环码排列
给你两个整数 n 和 start。你的任务是返回任意 (0,1,2,…,2^n-1) 的排列 p,并且满足:
p[0] = start
p[i] 和 p[i+1] 的二进制表示形式只有一位不同
p[0] 和 p[2^n -1] 的二进制表示形式也只有一位不同
实例:
实例
输入:n = 2, start = 3
输出:[3,2,0,1]
解释:这个排列的二进制表示是 (11,10,00,01)所有的相邻元素都有一位是不同的,另一个有效的排列是 [3,1,0,2]
思路与代码
题目与上面的是一样的,所有解决方法也是两种
思路一:找规律
观察格雷码的规律,具有一定的对称性,高位是 1 或者 0,并由此就行对称
代码一
class Solution {public List<Integer> circularPermutation(int n, int start) {List<Integer> ans = new ArrayList<>();Integer[] res = new Integer[1 << n];res[0] = 0;res[1] = 1;int count = 1;int index = start; // 找到位置, 存在start 为 0,1的问题,故直接赋值过去while (n-- > 1) {count <<= 1;for (int i = 0; i < count; i++) {res[i + count] = count + res[count - i - 1];if (res[i + count] == start) {index = i + count;}}}for (int i = 0; i < res.length; i++) {ans.add(res[(index + i) % res.length]);}return ans;}
}
思路二:与自然数之间的关系
要通过观察,格雷数的 ^ 关系,格雷是从0开始的,0^任意数都是本身,然后格雷数每个与前一个变化相差为一,故一直第一个数 ^ 结果就是你想要的
代码一:
class Solution {public List<Integer> circularPermutation(int n, int start) {List<Integer> res = new ArrayList<>();int sum = 1<<n;for(int i = 0;i < sum;i++){res.add((i >> 1) ^ i ^ start);}return res;}
}
相关文章:

LeetCode 格雷编码问题
格雷编码格雷编码的定义格雷编码的码表LeetCode 89. 格雷编码实例思路与代码思路一:找规律代码一代码二思路二:与自然数之间的关系(你必须知道,这个规律要去百度才知道)代码一LeetCode 1238. 循环码排列实例思路与代码…...

java生成html文件输出到指定位置
String fileName "filename.html";StringBuilder sb new StringBuilder();// 使用StringBuilder 构建HTML文件sb.append("<html>\n");sb.append("<head>\n");sb.append("<title>HTML File</title>\n");sb.a…...

华为OD机试用Python实现 -【微服务的集成测试】(2023-Q1 新题)
华为OD机试300题大纲 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 华为OD详细说明:https://dream.blog.csdn.net/article/details/128980730 微服务的集成测试…...
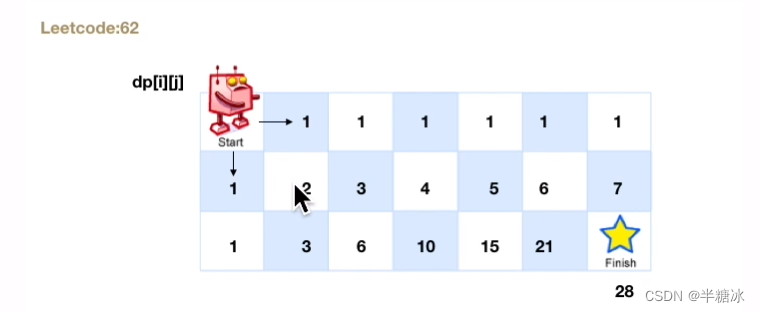
js版 力扣 62. 不同路径
一、题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径࿱…...

Qt音视频开发16-通用悬浮按钮工具栏的设计
一、前言 通用悬浮按钮工具栏这个功能经过了好几个版本的迭代,一开始设计的时候是写在视频控件widget窗体中,当时功能简单就放一排按钮在顶部悬浮widget中就好,随着用户需求的变化,用户需要自定义悬浮条的要求越发强烈࿰…...

商品比价API使用说明
商品数据分析 国内最早的比价搜索平台,专注于电商大数据的分析,有10年技术和数据沉淀。 公司自主研发的爬虫、搜索引擎、分布式计算等技术, 实现了对海量电商数据的及时监测、清洗和统计。 数据丰富 详细使用api 数据采集维度ÿ…...

基于 TensorFlow 的植物识别教程
首先,需要准备一些训练数据集。这些数据集应该包含两个文件夹:一个用于训练数据,另一个用于测试数据。每个文件夹应该包含子文件夹,每个子文件夹对应一个植物的种类,并包含该植物的图像。接下来,我们需要使…...

渗透测试之主机探测存活性实验
渗透测试之主机探测存活性实验实验目的一、实验原理1.1 TCP/IP协议1. TCP2. IP1.2 Ping的原理二、实验环境2.1 操作机器2.2 实验工具三、实验步骤1. 学会使用ping命令2. 使用Nmap进行多种方式的探测总结实验目的 熟悉TCP/IP协议、Ping命令基本概念学习nmap、SuperScan扫描方式…...
好用的idea插件leetcode editor【详细安装指南】
如果你和我一样存在着如下困扰: 上班想摸鱼刷leetcode,但是直接打开leetcode界面太扎眼了或者为leetcode刷题不可以debug而发愁 那今天分享的一款IDEA插件可以统统解决上述问题,插件名字叫leetcode editor,你可以直接在plugins中…...

二氧化碳地质封存技术应用前景及模型构建实践方法与讨论
2022年七月七日,工业和信息化部、发展改革委、生态环境部关于印发工业领域碳达峰实施方案的通知落地。全国各省份积极响应,纷纷出台地方指导文件,标志着我国碳减排事业的全面铺开。二氧化碳地质封存技术作为实现我国“双碳”目标的重要一环&a…...
STM32开发(12)----CubeMX配置WWDG
CubeMX配置窗口看门狗(WWDG)前言一、窗口看门狗的介绍二、实验过程1.STM32CubeMX配置窗口看门狗2.代码实现3.硬件连接4.实验结果总结前言 本章介绍使用STM32CubeMX对窗口看门狗定时器进行配置的方法。门狗本质上是一个定时器,提供了更高的安…...
JVM18运行时参数
4. JVM 运行时参数 4.1. JVM 参数选项 官网地址:https://docs.oracle.com/javase/8/docs/technotes/tools/windows/java.html 4.1.1. 类型一:标准参数选项 > java -help 用法: java [-options] class [args...](执行类)或 java [-options] -jar …...
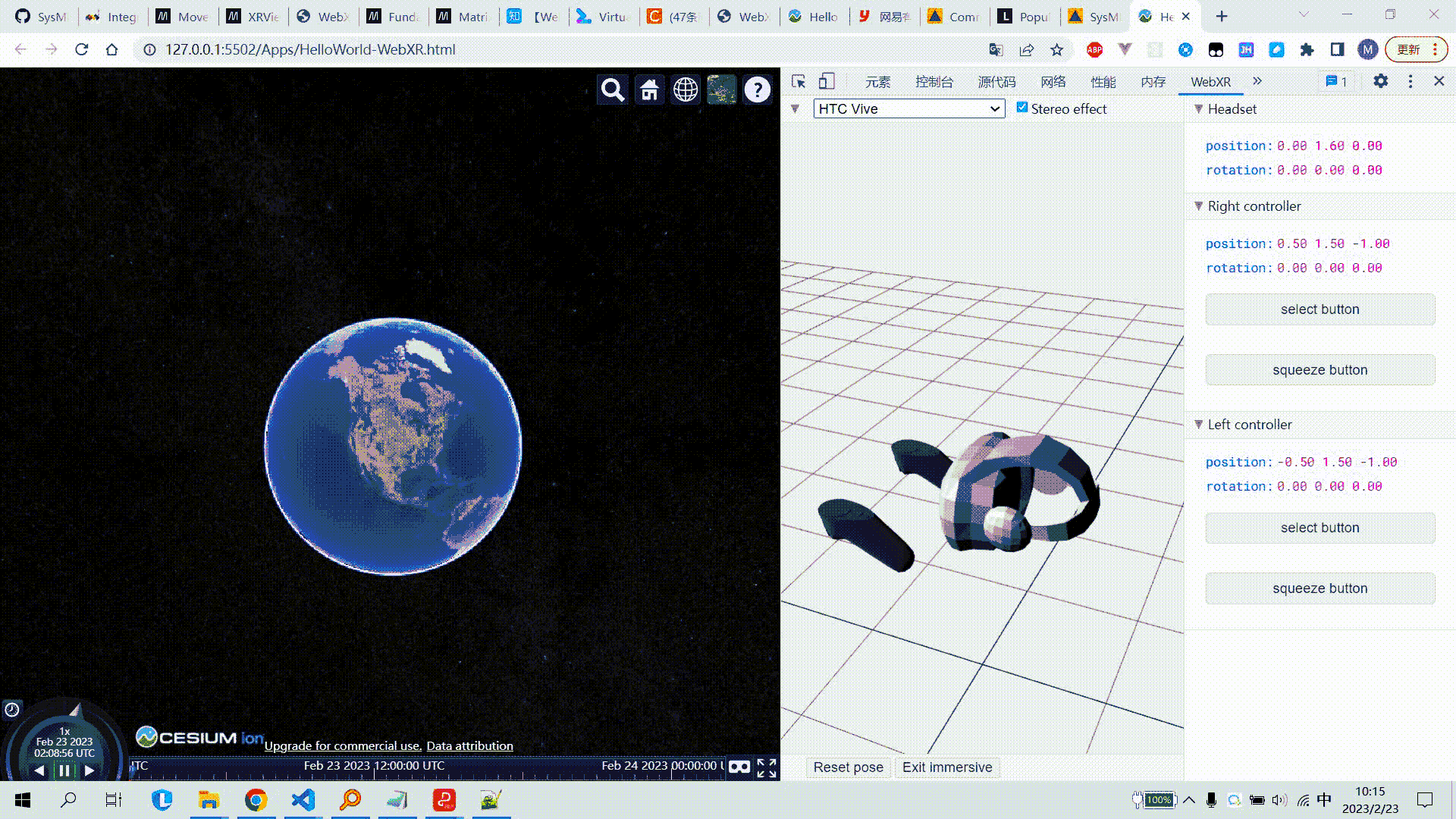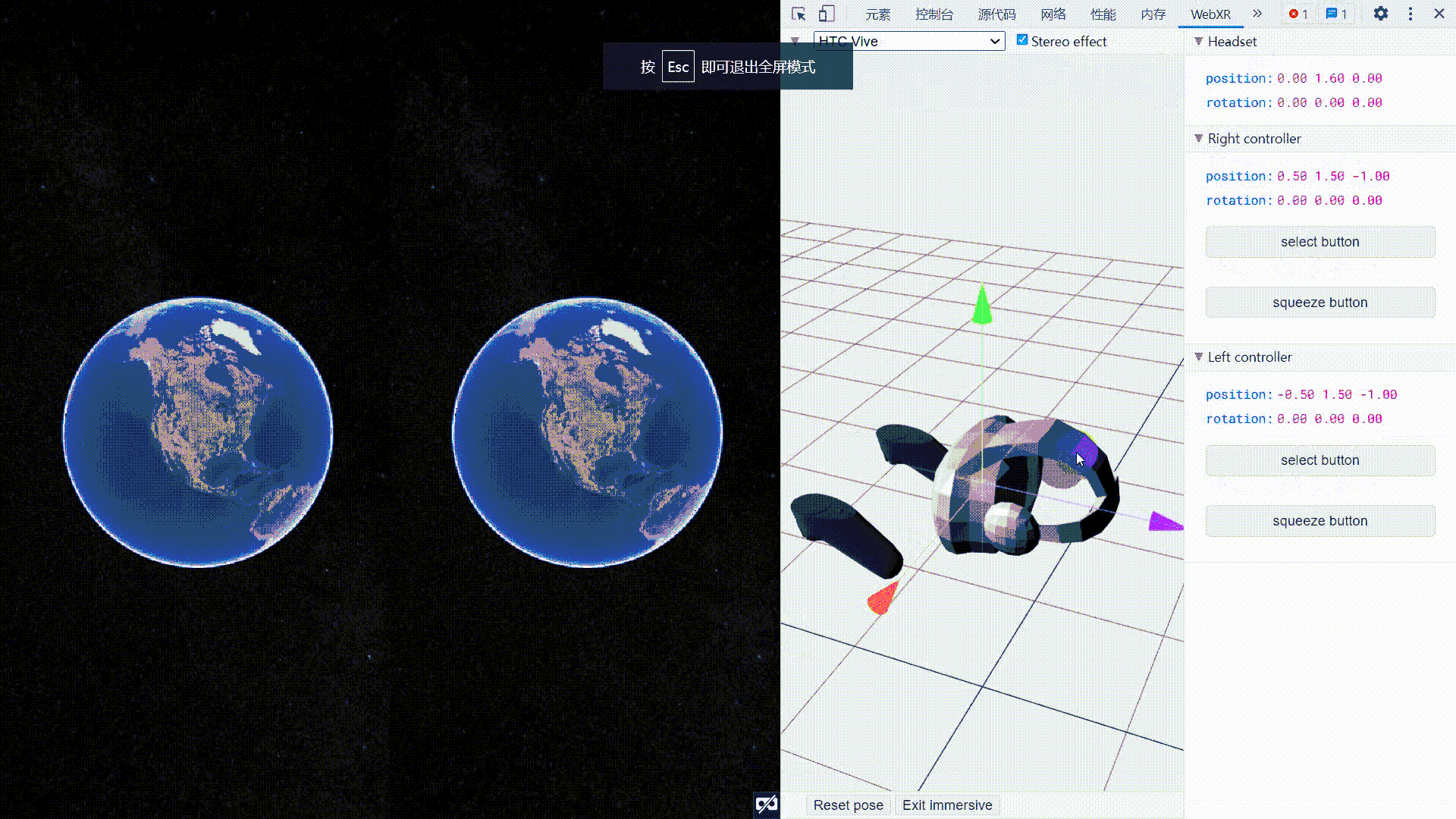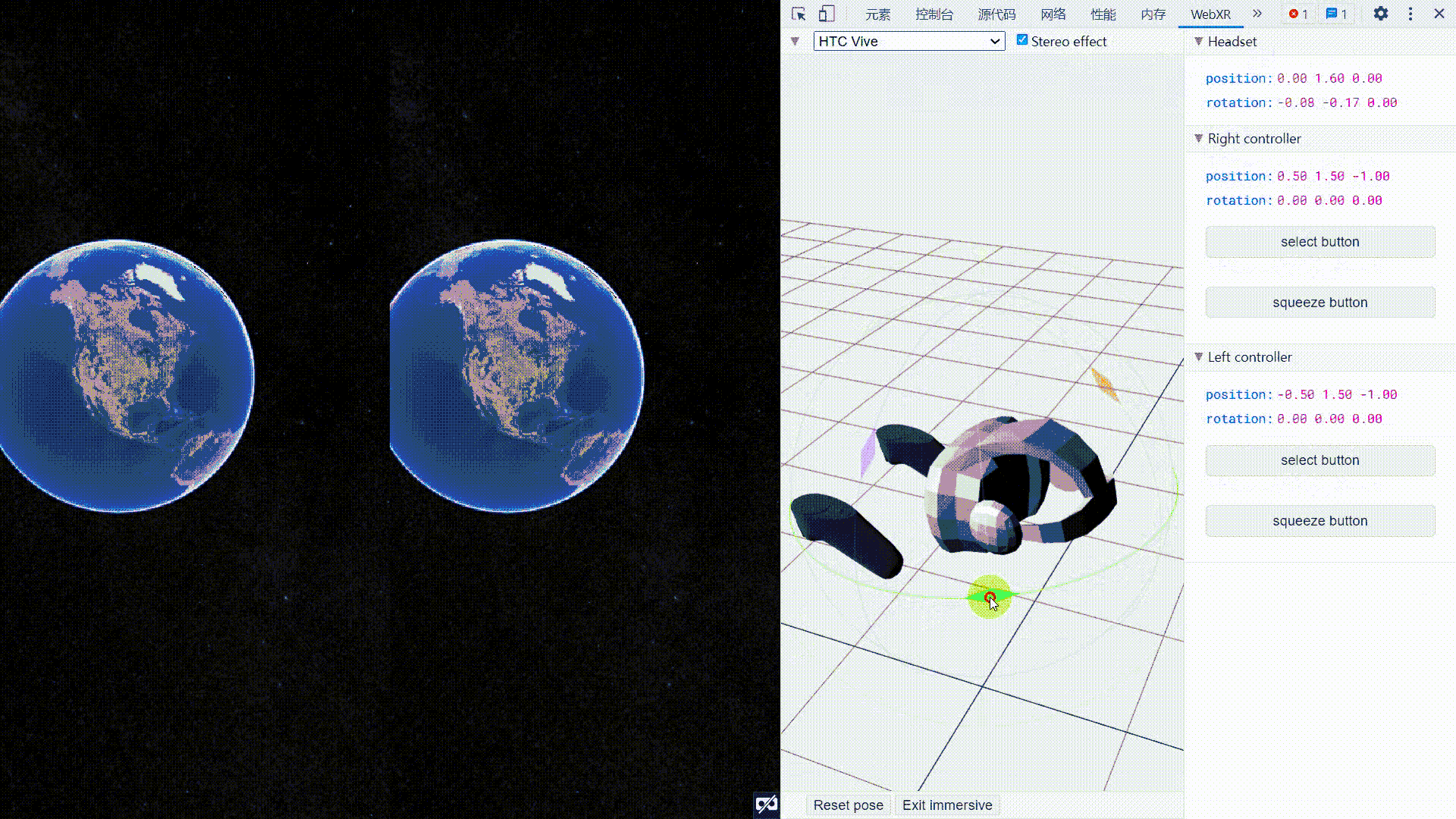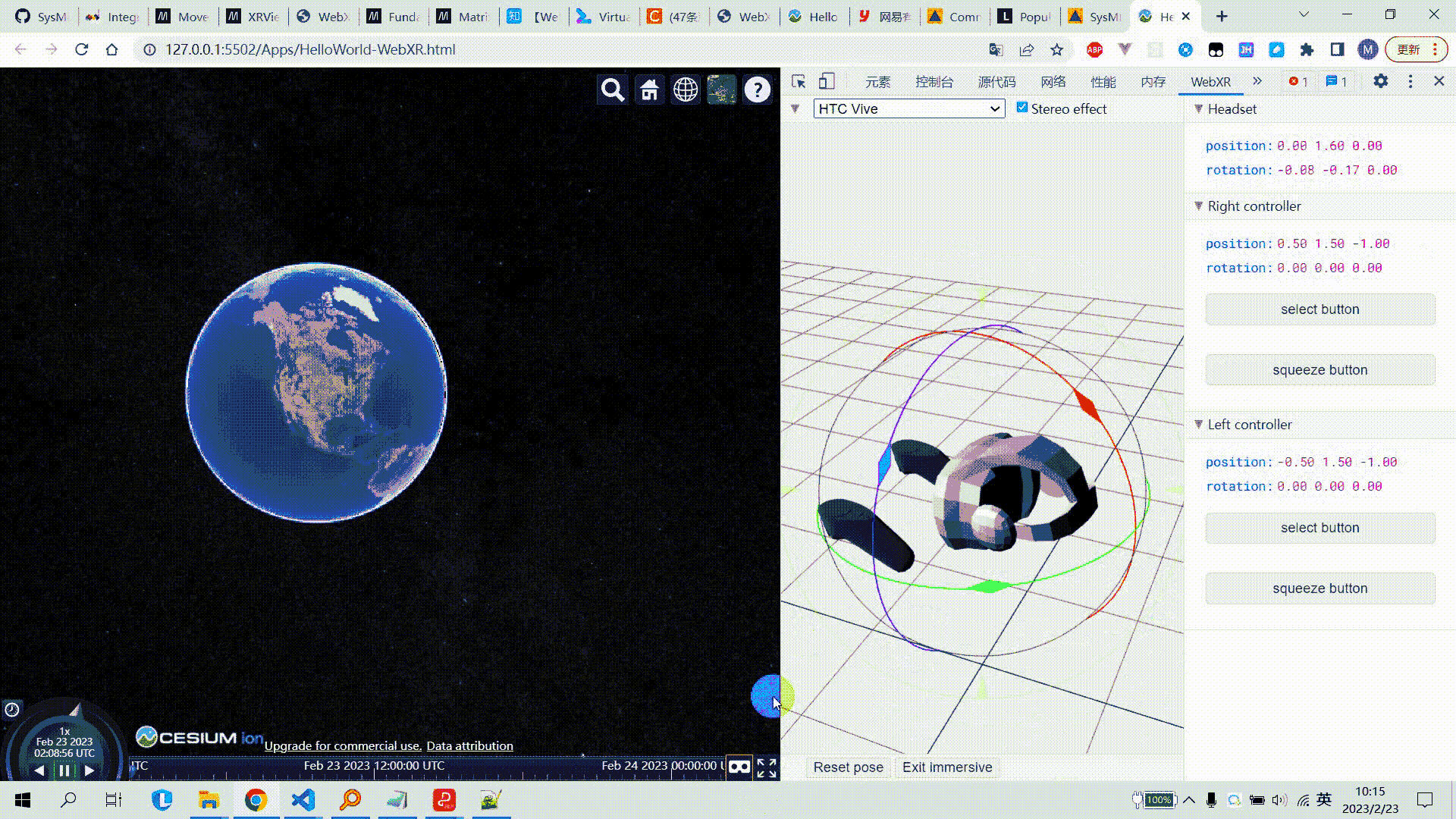
Cesium集成WebXR_连接VR设备
Cesium集成WebXR 文章目录Cesium集成WebXR1. 需求2. 技术基础2.1 WebGL2.2 WebXR2.3 其他3. 示例代码4. 效果图5. 参考链接1. 需求 通过WebXR接口,将浏览器端连接到VR头盔,实现在VR头盔中浏览Cesium场景,并可将头盔旋转的操作同步映射为场景…...

物联网在物流行业中的应用
物流管理需要同时监控供应链、仓储、运输等多项活动,然而许多因素会影响物流流程本身并导致延迟。为了简化流程和提高客户满意度,一些行业领导者和决策者积极创新,不断评估并使用物联网对物流流程的成本效益进行深入优化。在本文中࿰…...

<c++> 类与对象 | 面向对象 | 访问说明符 | 类的声明 | 创建类
文章目录前言面向过程编程面向对象编程什么是类类和结构体有什么区别三个访问说明符如何创建一个类类的声明创建类申明和定义全部放在类中声明和定义分离前言 从这里我们正式开始学习c中的面向对象编程,在学习之前,我们有必要了解一下什么是面向对象编程…...

恭喜!龙蜥社区荣登 2022 科创中国“开源创新榜”
2 月 20 日,中国科协召开以“创新提振发展信心,科技激发产业活力”为主题的2023“科创中国”年度会议。会上,“科创中国”联合体理事长、中国工程院院士周济介绍了 2022 年系列榜单征集遴选情况,并与中国科协副主席、中国工程院院…...

2023双非计算机硕士应战秋招算法岗之机器学习基础知识
目录 特征工程 2 缺失值处理 15 评价指标 33 逻辑回归 37 决策树 40 随机森林 46 SVM 49 Knn 56 Kmeans 59 PCA 66 朴素贝叶斯 68 常见分类算法的优缺点 72 特征工程 1.什么是特征工程 有这么一句话在业界广泛流传,数据和特征决定了机器学习的上限,而模型…...

二、TS的基础类型、类型注解
TS的基础类型、类型注解 TS的基础类型 js的数据类型: 基础数据类型(7个) boolean string number null undefined BigInt Symbol 引用数据类型(1个) Object 变量后面多了一个注解,注解为变量限定数据类型&…...

3年经验,3轮技术面+1轮HR面,拿下字节30k*16薪offer,这些自动化测试面试题值得大家借鉴
面试一般分为技术面和hr面,形式的话很少有群面,少部分企业可能会有一个交叉面,不过总的来说,技术面基本就是考察你的专业技术水平的,hr面的话主要是看这个人的综合素质以及家庭情况符不符合公司要求,一般来…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

