算法通关村 | 透彻理解动态规划
1. 斐波那契数列
1,1,2,3,5,8,13,..... f(n) = f(n-1) + f(n-2)
代码实现
public static int count_2 = 0;public int fibonacci(int n){if (n <= 2){count_2++;return n;}int f1 = 1;int f2 = 2;int sum = 0;for (int i = 3; i < n; i++) {count_2++;sum = f1 + f2;f1 = f2;f2 = sum;}return sum;}当n=20时,count是21891次,当n=30的时候结果是2692537,接近270万,为什么这么高,因为里面存在大量的循环,下面图中,n=8时,f(6)就重复计算两次,很多结点会被重复计算。
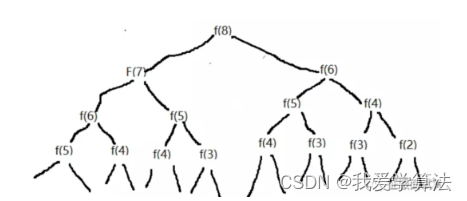
如何将其优化减少重复计算,这也是下面推导动态规划需要考虑的,可以将计算结果保存到数组中,f(n)的值保存在数组中,f(n)=arr[n],某个位置已经被计算出来,下次需要的时候直接取出来,不需要再递归。
public static int[] arr = new int[50];public static int count_3 = 0;public static void main(String[] args) {Arrays.fill(arr,-1);arr[0] = 1;System.out.println(fibonacci(31));}static int fibonacci(int n){if (n == 2 || n == 1){count_3++;arr[n] = n;return n;}if (arr[n] != -1){count_3++;return arr[n];}else {count_3++;arr[n] = fibonacci(n - 1) + fibonacci(n - 2);return arr[n];}}2 路径连环炮
文中的动态规划我们简称DP,路径相关的问题来分析动态规划,路径问题易于画图,方便理解,循序渐进的理解DP
2.1 第一炮:基本问题统计路径总数
LeetCode62 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
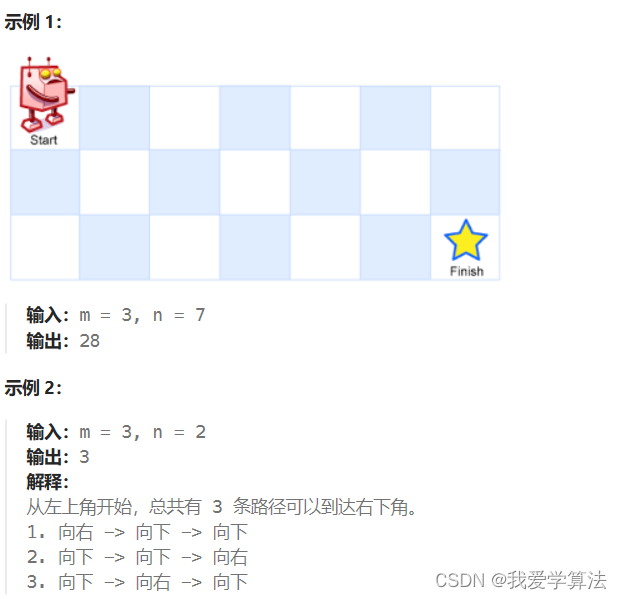
第一炮,我们研究如何通过递归来解决此问题,如下图所示,从起点开始要么向右,要么向下,每一种否会导致剩下的区间减少了一列或一行,形成两个不同区间的过程,每个区间继续以红点为起点继续上述操作,所以这就是一个递归的过程,

从图中寻找规律,目标从起点到终点,只能向右或向下,
1. 向右走一步,起点下面灰色的不会再被访问,后面剩一个3X1的矩阵,只能一直往下走,只有一种路径,
2. 向下走一步,起点右侧不不能再被访问,剩一个2X2的矩阵,还剩两种路径,
这是3X2的矩阵,一共有3中路径,一个2X2的矩阵和3X1的矩阵路径之和。
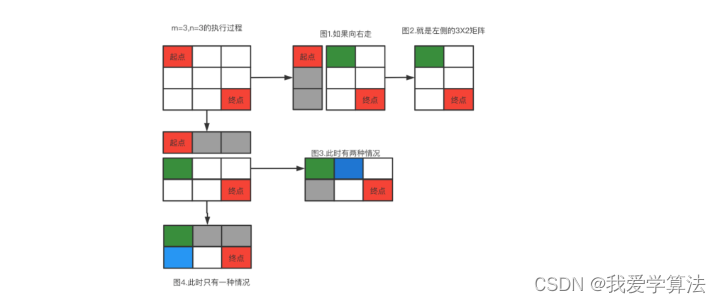
同样我们推导一个3X3的矩阵,就是一个3X2的矩阵和2X3的路径之和,
所以,对于一个mxn的矩阵,求路径的方法是serch(m,n)=search(m-1,n)+search(m,n-1);
public int uniquePath(int m,int n){return search(m,n);}private int search(int m, int n) {if (m == 1 || n == 1){return 1;}return search(m-1,n) + search(m,n-1);}对于3X3的矩阵,我们可以用二叉树表示
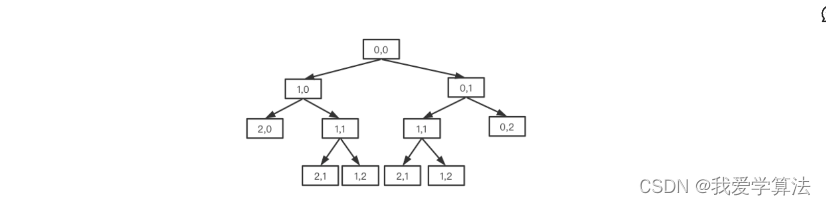
我们可以发现,和文章开头我们提到的一样,中间有重复计算,1,1计算了两次,那么如何优化
2.2 第二炮:使用二维数组优化递归
我们知道上面出现了重复计算,{1,1}出现两次,在{1,1}位置处,不管是从{0,1}还是{1,0}到来,都会产生两种走法,我们可以用二维数组记忆化搜索就不用两次遍历了,

每个格子都表示从起点开始到当前的位置有几种方式,这样我们通过计算路径的时候可以先查下二维数组有没有记录,有就直接读,没有再计算,这样就可以避免大量的重复计算,这就是记忆化搜索。
从上面的分析我们得到两个规律:
1.第一行和第一列都是1.
2.其他格子的值都是其左侧和上方格子之和,对于mXn的格子都适应。
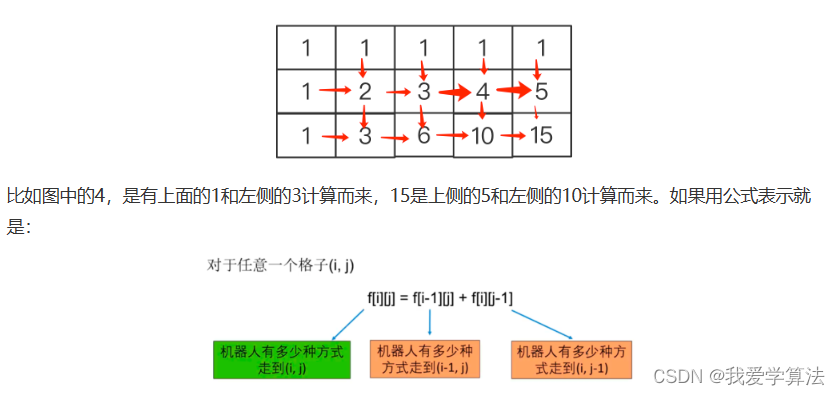
public int uniquePath(int m, int n){int[][] f = new int[m][n];f[0][0] = 1;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (i > 0 && j > 0){f[i][j] = f[i -1][j] + f[i][j -1];}else if (i > 0){f[i][j] = f[i -1][j];} else if (j > 0) {f[i][j] = f[i][j -1];}}}return f[m -1][n -1];}2.3 第三炮:滚动数组:用一维代替二维数组
第三炮,我们通过滚动数组来优化此问题,上面缓存空间使用二维数组,占据空间大,能否进一步优化,我们看上面的二维数组找出规律。
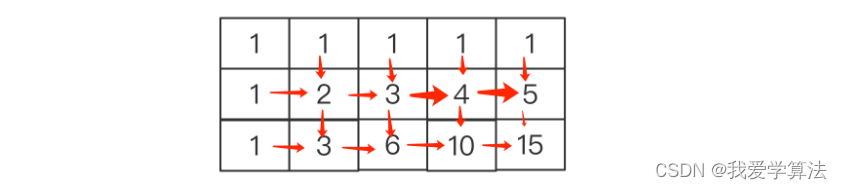
发现除了第一行和第一列都是1外,每个位置都是其左侧和上方的格子之和,可以用一个大小为n的一维数组来解决:
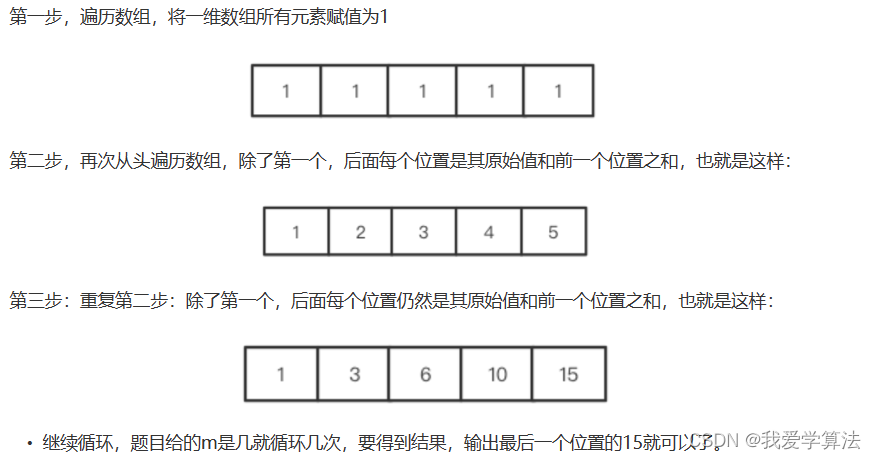
将几个一维数组拼接起来,就是和上面的二维数组完全一样的,反复更新数组的策略就是滚动数组,计算公式是:dp[j] = dp[j]+dp[j-1]
public int uniquePaths(int m, int n){int[] dp = new int[n];//将数组初始元素初始为1Arrays.fill(dp,1);for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {//等式左边的dp[j]是上一次计算后的,再加上左边的dp[j-1]即为当前结果dp[j] = dp[j] + dp[j - 1];}}return dp[n -1];}这个题目包含了DP(动态规划)里的多个方面,比如重复子问题、记忆化搜索、滚动数组等等,这就是最简单的动态规划了,只不过我们这里的规划是dp[j] = dp[j] + dp[j -1] ;不用进行复杂的比较和计算。
3. 理解动态规划
DP一般是让我们找最值的,例如最长公共子序列,最关键的是DP问题的子问题不是相互独立的,如果递归直接分解会导致重复计算指数级增长,开头的热身题,而DP的最大价值是为了消除冗余,加速计算。
动态规划解决什么问题:A求有多少种走法,B输出所有的走法
动态规划计算效率高,但是不能找到满足要求的路径,
区分动态规划和递归最重要的一条是:动态规划只关心当前结果是什么,怎么来的就不管了,所以动态规划无法获得完整的路径,这与回溯不一样,回溯能够获得一条甚至所有满足要求的完整路径。
DP的基本思想是将待求解问题分解成若干个子问题,先求子问题,再从这些子问题中得到原问题的解,既然要找最值,那么必然要做的就是穷举来找所有的可能,然后选择“最”的那个,这就是为什么再DP代码中大量判断逻辑都会被套上min()或者max(),
既然穷举,那为什么还有DP的概念?这是因为穷举的过程中存在大量的重复计算,效率低下,所以我们要使用记忆化搜索等方式来消除不必要的计算,所谓记忆化搜索就是将已经计算好的结果先存在数组里面,后面就直接读就不再重复计算了,
既然记忆化能解决问题,为啥DP这么难,因为DP问题一定具备“最优子结构”,这样才能让记忆时得到准确结果,至于什么时最优子结构,后面还有具体问题,
有了最优子结构,还要正确的“状态转移方程”,才能正确的穷举,也就是递归关系,大部分递归都可以通过数组实现,因此代码结构一般是这样的for循环,这就是DP的基本模板:
//初始化base case ,也就是刚开始的几种场景,有几种枚举
dp[0][0][...] = base case
//进行状态转移
for 状态1 状态1的所有取值
for 状态2 in 状态2的所有取值
dp[状态1][状态2] = 求最值Max(选择1,选择2,...)
动态规划题目有三种基本类型:
1. 计数有关,例如求多少种方式到右下角,有多少种方式选出K个数是使得什么什么的问题,不关心路径是什么
2. 求最大值最小值,最多最少等,例如最大数字和,最长上升子序列,最长公共子序列,最长回文序列等
3. 求存在性,例如取石子游戏,先手是否必胜,能不能选出k个数使得什么什么等等
不管那种解决问题的模板也是类似的
- 第一步:确定状态和子问题,也就是枚举出某个位置所有的可能性,对于DP,大部分题目分析最后一步更容易一些,得到递推关系,同时将问题转换为子问题。
- 第二步:确定状态转移方程,也就是数组要存储什么内容,很多时候状态确定之后,状态转移方程也就确定了,前两步也可作为为第一步骤
- 第三步:确定初始和边界条件情况,注意细心,尽量周全
- 第四步:按照从小到大的顺序计算:f[0],f[1],f[2]
我们自始至终,都要在大脑里装一个数组(可能是一维,也可能是二维),要看这个数组每个元素的含义是什么(也就是状态),要看每个数组是根据谁来算的(状态转移方程),然后就是从小到大挨着将数组填满(从小到大计算,实现记忆化搜索),最后看那个位置是我们想要的结果。
相关文章:

算法通关村 | 透彻理解动态规划
1. 斐波那契数列 1,1,2,3,5,8,13,..... f(n) f(n-1) f(n-2) 代码实现 public static int count_2 0;public int fibonacci(int n){if (n < 2){count_2;return n;}int f1 1;int f2 2;i…...
)
数据结构(持续更新)
嗯,怎么说数据结构果然很玄妙。按照能不能存储多行元素大致分为两类。 不能存好几行的数据包括pair,int,float,double,char,struct; 能存好几行的:map,unordered_map,list,vector,set,string,array。 1. pair “pair” 是 C++ 标准库中的一个模板类,它用于存储…...
nginx部署vue后显示500 Internal Server Error解决方案
前言 描述:当我配置好全部之后,通过 服务器 ip 地址访问,遇到报错信息:500 Internal Server Error。 今天部署vue前端项目一直报错500,无法显示出主页面。 一个以为是自己的dist位置没有访问正确或者nginx.conf的位…...

微调大型语言模型(一):为什么要微调(Why finetune)?
今天我们来学习Deeplearning.ai的在线课程 微调大型语言模型(一)的第一课:为什么要微调(Why finetune)。 我们知道像GPT-3.5这样的大型语言模型(LLM)它所学到的知识截止到2021年9月,那么如果我们向ChatGPT询问2022年以后发生的事情,它可能会…...

【GO】网络请求例子
post请求;multipart/form-data类型 // 构建请求参数requestData : map[string]interface{}{"gb": "","code": "","reMemberInfo": map[string]interface{}{"shi": "","…...

泡泡玛特海外布局动作不断,开启东南亚潮玩盛会
近日,泡泡玛特海外布局动作不断,9月8日至10日,泡泡玛特2023 PTS潮流玩具展(下简称新加坡PTS)在新加坡滨海湾金沙成功举办,现场人气爆棚,三天吸引了超过2万观众入场,这也是泡泡玛特首…...
uniappAndroid平台签名证书(.keystore)生成
一、安装JRE环境 https://www.oracle.com/java/technologies/downloads/#java8 记住下载默认安装地址。ps:我都默认安装地址C:\Program Files\Java\jdk-1.8 二、安装成功后配置环境变量 系统变量配置 AVA_HOME 放到环境变量去 %JAVA_HOME%\bin 三、生成签名证书…...
Gateway学习和源码解析
文章目录 什么是网关?搭建实验项目demo-servicegateway-service尝试简单上手 路由(Route)断言(Predicate)和断言工厂(Predicate Factory)gateway自带的断言工厂After(请求必须在某个…...
移动机器人运动规划 --- 基于图搜索的Dijkstra算法
移动机器人运动规划 --- 基于图搜索的Dijkstra算法 Dijkstra 算法Dijkstra 算法 伪代码流程Dijkstra 算法步骤示例Dijkstra算法的优劣分析 Dijkstra 算法 Dijkstra 算法与BFS算法的区别就是 : 从容器中弹出接下来要访问的节点的规则不同 BFS 弹出: 层级最浅的原则,…...

Mybatis SQL构建器
上一篇我们介绍了在Mybatis映射器中使用SelectProvider、InsertProvider、UpdateProvider、DeleteProvider进行对数据的增删改查操作;本篇我们介绍如何使用SQL构建器在Provider中优雅的构建SQL语句。 如果您对在Mybatis映射器中使用SelectProvider、InsertProvider…...
怎么将几张图片做成pdf合在一起
怎么将几张图片做成pdf合在一起?在我们平时的工作中,图片和pdf都是非常重要的电脑文件,使用也非常频繁,图片能够更为直观的展示内容,而pdf则更加的正规,很多重要文件大多会做成pdf格式的。在职场人的日常工…...
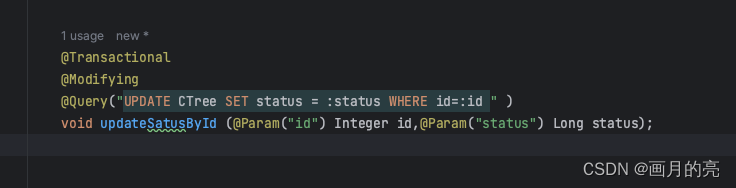
关于JPA +SpringBoot 遇到的一些问题及解决方法
关于JPA SpringBoot 遇到的一些问题及解决方法(可能会有你正在遇到的) 一、JpaRepository相关 1.1 org.springframework.dao.InvalidDataAccessResourceUsageException: Named parameter not bound : id; nested exception is org.hibernate.QueryEx…...

全国馆藏《乡村振兴战略下传统村落文化旅游设计》许少辉八一著作——2023学生开学季辉少许
全国馆藏《乡村振兴战略下传统村落文化旅游设计》许少辉八一著作——2023学生开学季辉少许...

linux升级glibc-2.28
1.准备工作 1.1升级gcc到gcc8 # 安装devtoolset-8-gcc yum install centos-release-scl yum install devtoolset-8 scl enable devtoolset-8 -- bash# 启用工具 source /opt/rh/devtoolset-8/enable # 安装GCC-8 yum install -y devtoolset-8-gcc devtoolset-8-gcc-c devtoolse…...
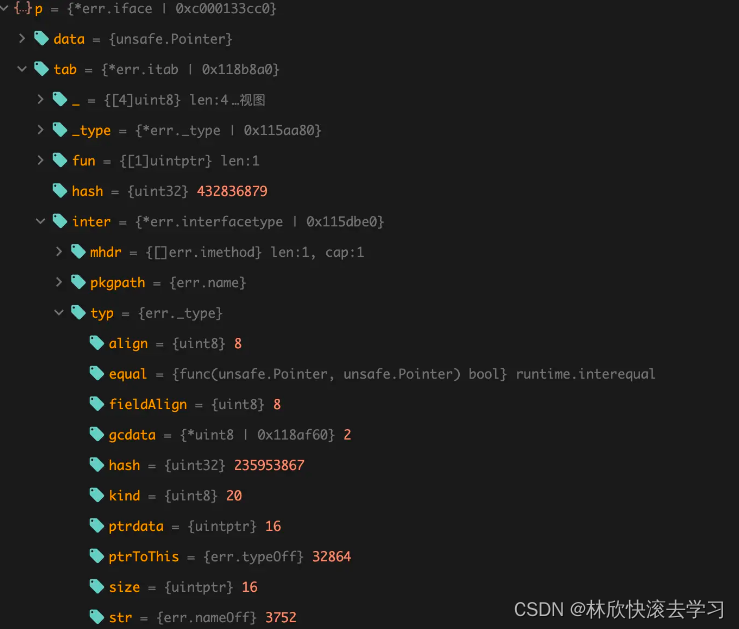
[Go疑难杂症]为什么nil不等于nil
现象 在日常开发中,可能一不小心就会掉进 Go 语言的某些陷阱里,而本文要介绍的 nil ≠ nil 问题,便是其中一个,初看起来会让人觉得很诡异,摸不着头脑。 先来看个例子: type CustomizedError struct {Err…...

C#60个常见的问题和答案
在本文中,我将帮助你准备好在下一次面试中解决这些与C# 编程语言相关的问题。同时,你可能想练习一些C# 项目。这 60 个基本的 C#面试问题和答案将帮助你了解该语言的技术概念。 目录 什么是 C#? 1.什么是类? 2.面向对象编程的主要概念是什么?...

11:STM32---spl通信
目录 一:SPL通信 1:简历 2:硬件电路 3:移动数据图 4:SPI时序基本单元 A : 开/ 终条件 B:SPI时序基本单元 A:模式0 B:模式1 C:模式2 D:模式3 C:SPl时序 A:发送指令 B: 指定地址写 C:指定地址读 二: W25Q64 1:简历 2: 硬件电路 3:W25Q64框图 4: Flash操作注意…...
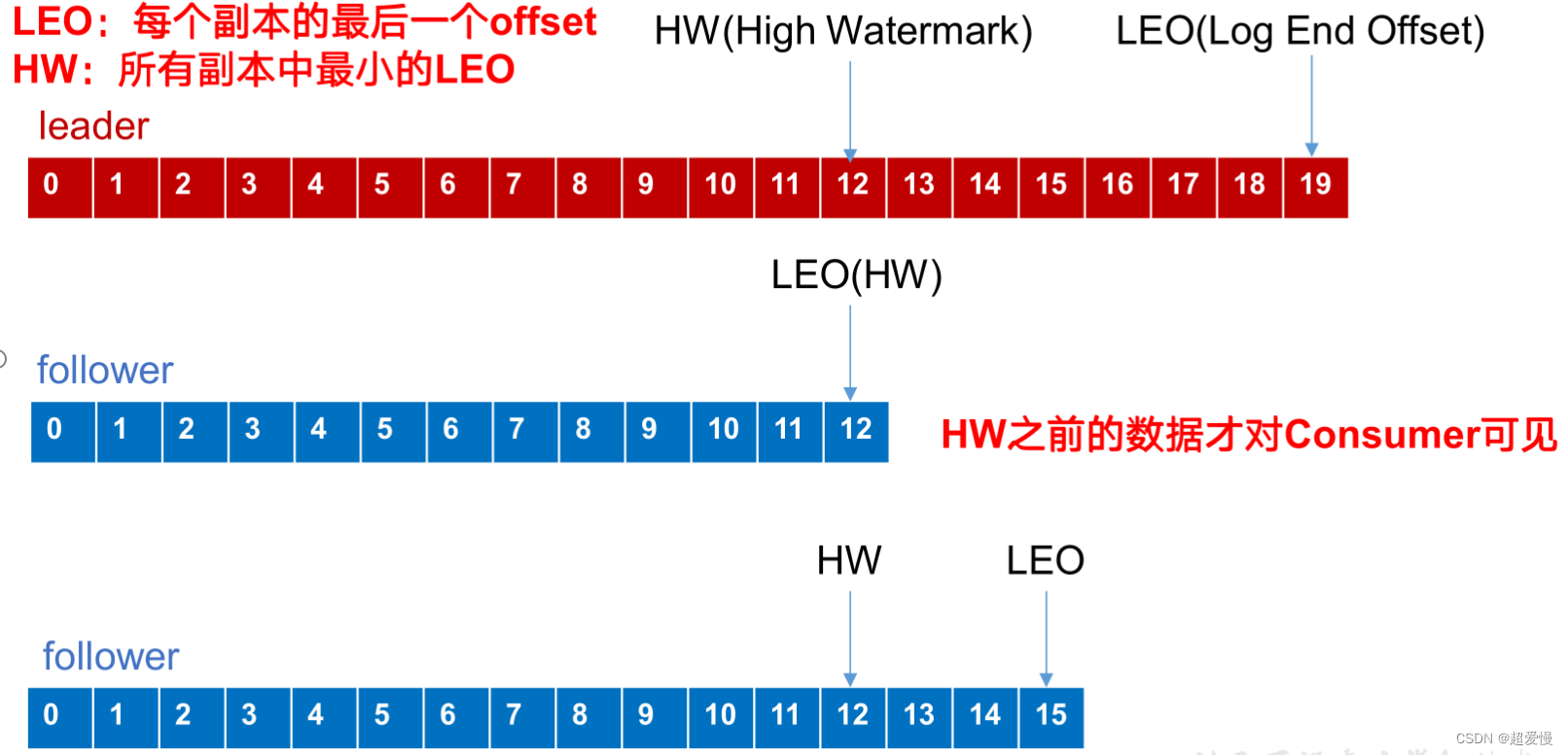
kafka的 ack 应答机制
目录 一 ack 应答机制 二 ISR 集合 一 ack 应答机制 kafka 为用户提供了三种应答级别: all,leader,0 acks :0 这一操作提供了一个最低的延迟,partition的leader接收到消息还没有写入磁盘就已经返回ack&#x…...
Django系列:Django开发环境配置与第一个Django项目
Django系列 Django开发环境配置与第一个Django项目 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/1328…...
iPad协议/微信协议最新版
一、了解微信的协议 在开发微信协议之前,需要先了解微信的协议。微信的协议包括登录协议、消息传输协议、文件传输协议、数据同步协议等。其中,登录协议是最重要的协议之一,包括登录验证、登录认证等。消息传输协议则是微信最核心的功能之一…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
