LeetCode 1337. The K Weakest Rows in a Matrix【数组,二分,堆,快速选择,排序】1224
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个大小为 m * n 的矩阵 mat,矩阵由若干军人和平民组成,分别用 1 和 0 表示。
请你返回矩阵中战斗力最弱的 k 行的索引,按从最弱到最强排序。
如果第 i 行的军人数量少于第 j 行,或者两行军人数量相同但 i 小于 j,那么我们认为第 i 行的战斗力比第 j 行弱。
军人 总是 排在一行中的靠前位置,也就是说 1 总是出现在 0 之前。
示例 1:
输入:mat =
[[1,1,0,0,0],[1,1,1,1,0],[1,0,0,0,0],[1,1,0,0,0],[1,1,1,1,1]],
k = 3
输出:[2,0,3]
解释:
每行中的军人数目:
行 0 -> 2
行 1 -> 4
行 2 -> 1
行 3 -> 2
行 4 -> 5
从最弱到最强对这些行排序后得到 [2,0,3,1,4]
示例 2:
输入:mat =
[[1,0,0,0],[1,1,1,1],[1,0,0,0],[1,0,0,0]],
k = 2
输出:[0,2]
解释:
每行中的军人数目:
行 0 -> 1
行 1 -> 4
行 2 -> 1
行 3 -> 1
从最弱到最强对这些行排序后得到 [0,2,3,1]
提示:
m == mat.lengthn == mat[i].length2 <= n, m <= 1001 <= k <= mmatrix[i][j]不是 0 0 0 就是 1 1 1
由于本题中的矩阵行数 m m m 和列数 n n n 均不超过 100 100 100 ,数据规模较小,因此我们可以设计出一些时间复杂度较高的方法,例如直接对整个矩阵进行一次遍历,计算出每一行的战斗力,再进行排序并返回最弱的 k k k 行的索引。
解法 二分查找 + 堆
题目描述中有一条重要的保证:军人总是排在一行中的靠前位置,也就是说 1 1 1 总是出现在 0 0 0 之前。因此,我们可以通过二分查找的方法,找出一行中最后的那个 1 1 1 的位置。如果其位置为 p o s pos pos ,那么这一行 1 1 1 的个数就为 p o s + 1 pos+1 pos+1 。特别地,如果这一行没有 1 1 1 ,那么令 p o s = − 1 pos=-1 pos=−1 。
当我们得到每一行的战斗力后,我们可以将它们全部放入一个小根堆中,并不断地取出堆顶的元素 k k k 次,这样我们就得到了最弱的 k k k 行的索引。
需要注意的是,如果我们依次将每一行的战斗力以及索引(因为如果战斗力相同,索引较小的行更弱,所以我们需要在小根堆中存放战斗力和索引的二元组)放入小根堆中,那么这样做的时间复杂度是 O ( m log m ) O(m\log m) O(mlogm) 的。一种更好的方法是使用这 m m m 个战斗力值直接初始化一个小根堆,时间复杂度为 O ( m ) O(m) O(m) 。可参考《算法导论》的 6.3 节了解该过程时间复杂度的证明方法。
class Solution {
public:vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();vector<pair<int, int>> power;for (int i = 0; i < m; ++i) {int l = 0, r = n - 1, pos = -1;while (l <= r) {int mid = (l + r) / 2;if (mat[i][mid] == 0) {r = mid - 1;}else {pos = mid;l = mid + 1;}}power.emplace_back(pos + 1, i);}priority_queue q(greater<pair<int, int>>(), move(power));vector<int> ans;for (int i = 0; i < k; ++i) {ans.push_back(q.top().second);q.pop();}return ans;}
};
复杂度分析:
- 时间复杂度: O ( m log n + k log m ) O(m\log n+k\log m) O(mlogn+klogm) :我们需要 O ( m log n ) O(m\log n) O(mlogn) 的时间对每一行进行二分查找。我们需要 O ( m ) O(m) O(m) 的时间建立小根堆。我们需要 O ( k log m ) O(k\log m) O(klogm) 的时间从堆中取出 k k k 个最小的元素。
- 空间复杂度: O ( m ) O(m) O(m) ,即为堆需要使用的空间。
解法 二分查找 + 快速选择
我们也可以通过快速选择算法,在平均 O ( m ) O(m) O(m) 的时间内不计顺序地内找出 k k k 个最小的元素,再使用排序算法在 O ( k log k ) O(k\log k) O(klogk) 的时间对这 k k k 个最小的元素进行升序排序,就可以得到最终的答案。参考「剑指 Offer 40. 最小的k个数」题解的方法三或者「215. 数组中的第K个最大元素」的题解方法一了解快速选择算法:
template<typename T>
class Helper {static int partition(vector<T>& nums, int l, int r) {T pivot = nums[r];int i = l - 1;for (int j = l; j <= r - 1; ++j) {if (nums[j] <= pivot) {i = i + 1;swap(nums[i], nums[j]);}}swap(nums[i + 1], nums[r]);return i + 1;}// 基于随机的划分static int randomized_partition(vector<T>& nums, int l, int r) {int i = rand() % (r - l + 1) + l;swap(nums[r], nums[i]);return partition(nums, l, r);}static void randomized_selected(vector<T>& arr, int l, int r, int k) {if (l >= r) {return;}int pos = randomized_partition(arr, l, r);int num = pos - l + 1;if (k == num) {return;} else if (k < num) {randomized_selected(arr, l, pos - 1, k);} else {randomized_selected(arr, pos + 1, r, k - num);}}public:static vector<T> getLeastNumbers(vector<T>& arr, int k) {srand((unsigned)time(NULL));randomized_selected(arr, 0, (int)arr.size() - 1, k);vector<T> vec;for (int i = 0; i < k; ++i) {vec.push_back(arr[i]);}return vec;}
};class Solution {
public:vector<int> kWeakestRows(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();vector<pair<int, int>> power;for (int i = 0; i < m; ++i) {int l = 0, r = n - 1, pos = -1;while (l <= r) {int mid = (l + r) / 2;if (mat[i][mid] == 0) {r = mid - 1;}else {pos = mid;l = mid + 1;}}power.emplace_back(pos + 1, i);}vector<pair<int, int>> minimum = Helper<pair<int, int>>::getLeastNumbers(power, k);sort(minimum.begin(), minimum.begin() + k);vector<int> ans;for (int i = 0; i < k; ++i) {ans.push_back(minimum[i].second);}return ans;}
};
复杂度分析
- 时间复杂度: O ( m log n + k log k ) O(m\log n + k\log k) O(mlogn+klogk) :我们需要 O ( m log n ) O(m\log n) O(mlogn) 的时间对每一行进行二分查找。我们需要 O ( m ) O(m) O(m) 的时间完成快速选择算法。我们需要 O ( k log k ) O(k\log k) O(klogk) 的时间对这 k k k 个最小的元素进行升序排序。
- 空间复杂度: O ( m ) O(m) O(m) ,即为快速选择算法中的数组需要使用的空间。
相关文章:

LeetCode 1337. The K Weakest Rows in a Matrix【数组,二分,堆,快速选择,排序】1224
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

如何使用Spring提供的Retry
0、本例中使用的是 springboot-2.0.4.RELEASE,jdk1.8 1、导包。需要注意版本。2.0.0需要spring6和jdk17 <dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId><version>1.3.4<…...
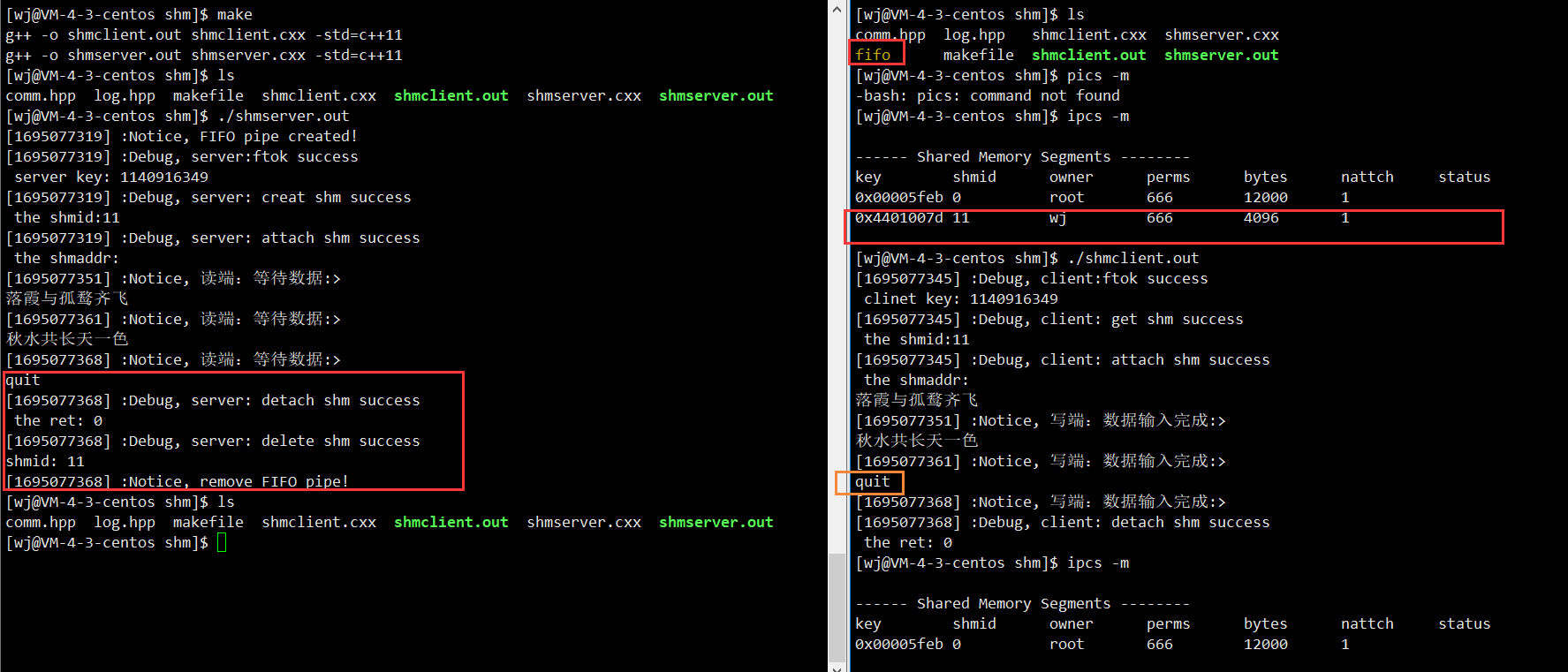
【ONE·Linux || 进程间通信】
总言 进程间通信:简述进程间通信,介绍一些通信方式,管道通信(匿名、名命)、共享内存等。 文章目录 总言1、进程间通信简述2、管道2.1、简介2.2、匿名管道2.2.1、匿名管道的原理2.2.2、编码理解:用fork来共…...
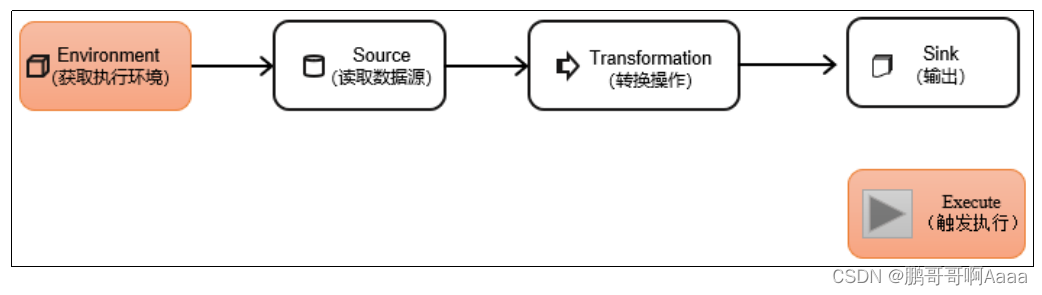
207.Flink(二):架构及核心概念,flink从各种数据源读取数据,各种算子转化数据,将数据推送到各数据源
一、Flink架构及核心概念 1.系统架构 JobMaster是JobManager中最核心的组件,负责处理单独的作业(Job)。一个job对应一个jobManager 2.并行度 (1)并行度(Parallelism)概念 一个特定算子的子任务(subtask)的个数被称之为其并行度(parallelism)。这样,包含并行子任…...
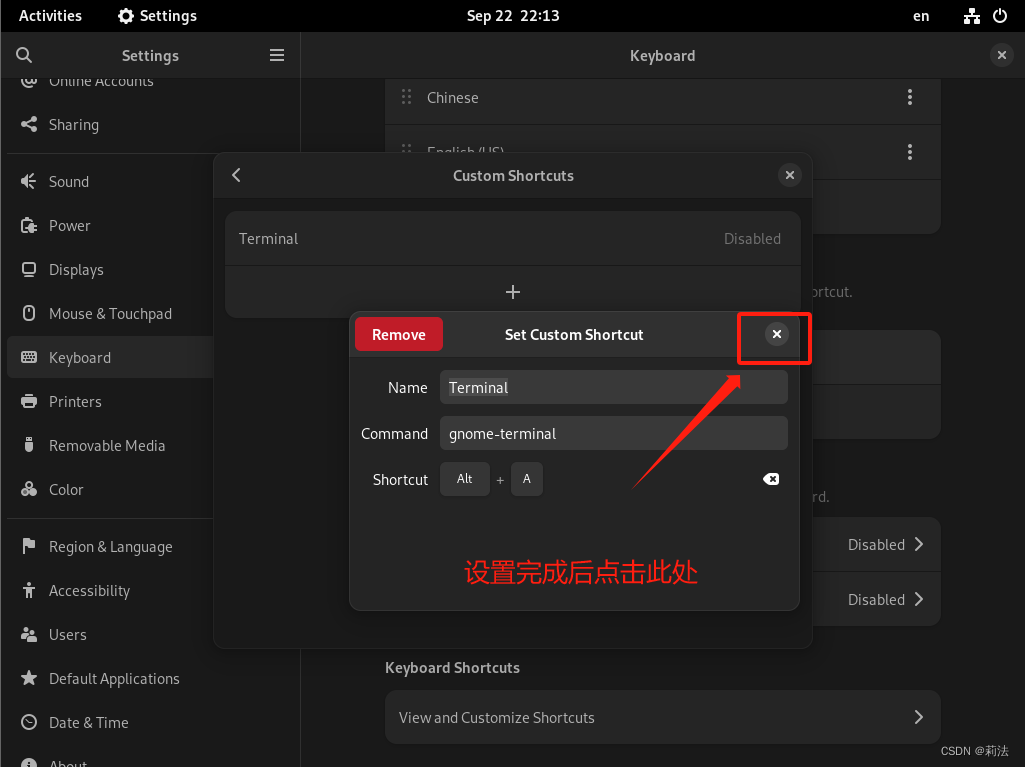
debian终端快捷键设置
为了方便使用图形化debian,快捷调出shell终端是提升工作学习效率的最重要的一步。 1.首先点击右上角,选择设置 2.点击键盘,选择快捷键,并创建自定义快捷键 3.点击添加快捷键 4.根据图中提示创建快捷键 Name: Terminal Command…...

原生ajax
什么是Ajax Asynchronous JavaScript and xml 异步的 js 和 xml(数据承载方式) ,本质:使用js提供的异步对象XMLHttpRequest 异步的向服务器提交请求,并且接受服务器响应回来的数据。 使用ajax 1.创建异步对象 var xhrnew XMLHttp…...
:并发编程)
面试题库(五):并发编程
多线程类的使用 java线程同步有哪些方法、各自的优缺点synchronized 和ReentrantLock区别,可重入锁是什么?threadlocal有什么用Java中创建线程有几种方式?分别是? 当主线程执行结束后,子线程还会继续执行下去吗?JUC中有哪些常用的集合?(项目中用到的)CopyOnWriteArray…...

Android FileProvider笔记
一、FileProvider是什么 通过FileProvider.getUriForFile(NonNull Context context, NonNull String authority, NonNull File file)方法获得一个有临时权限的Uri给客户端用来访问本APP文件。 当然看FileProvider类的注释更加详细 二、代码示例 <providerandroid:name&q…...
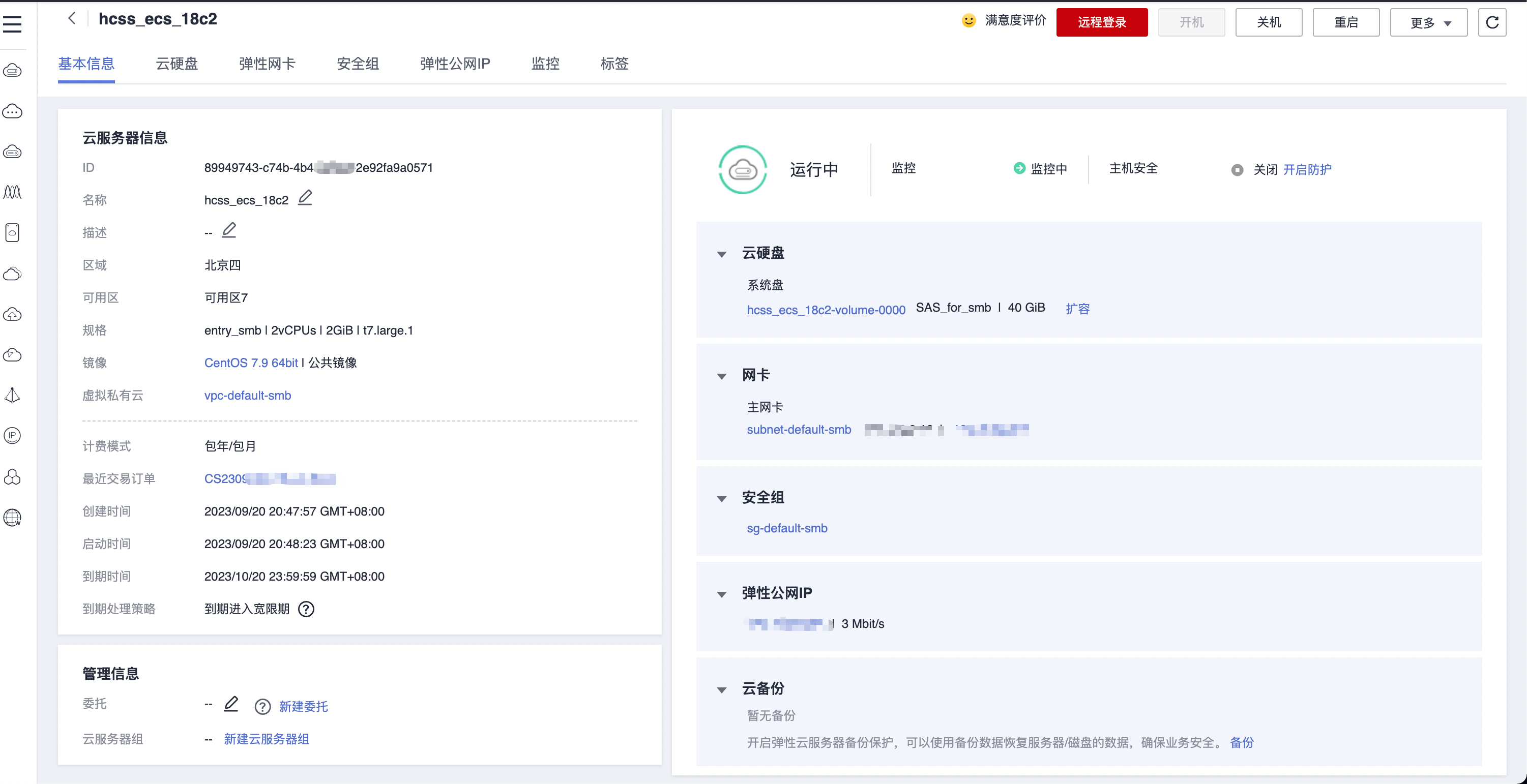
华为云云耀云服务器L实例评测 |云服务器选购
华为云耀云服务器 L 实例是一款轻量级云服务器,开通选择实例即可立刻使用,不需要用户再对服务器进行基础配置。新用户还有专享优惠,2 核心 2G 内存 3M 带宽的服务器只要 89 元/年,可以点击华为云云耀云服务器 L 实例购买地址去购买…...

2023-09-22 LeetCode每日一题(将钱分给最多的儿童)
2023-09-22每日一题 一、题目编号 2591. 将钱分给最多的儿童二、题目链接 点击跳转到题目位置 三、题目描述 给你一个整数 money ,表示你总共有的钱数(单位为美元)和另一个整数 children ,表示你要将钱分配给多少个儿童。 你…...

功能测试的重要性
前言 在软件开发领域,功能测试是确保软件质量的关键步骤之一。正如其名称所示,功能测试是验证软件产品是否具有其描述的功能和符合预期结果的过程。这种类型的测试非常重要,因为它不仅可以帮助团队检测潜在的缺陷并提高软件品质,…...

《Linux高性能服务器编程》--高级I/O函数
目录 1--Pipe() 2--dup() 和 dup2() 3--readv() 和 writev() 4--sendfile() 5--mmap() 和 munmap() 6--spice() 7--tea() 8--fcntl() 1--Pipe() #include <unistd.h> int pipe(int fd[2]); // 成功返回0,失败返回-1 pipe() 函数可用于创建一个管道&a…...
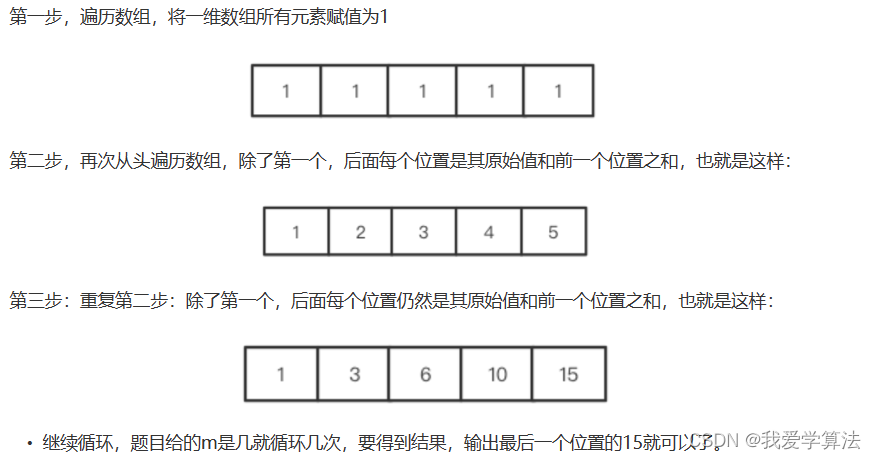
算法通关村 | 透彻理解动态规划
1. 斐波那契数列 1,1,2,3,5,8,13,..... f(n) f(n-1) f(n-2) 代码实现 public static int count_2 0;public int fibonacci(int n){if (n < 2){count_2;return n;}int f1 1;int f2 2;i…...
)
数据结构(持续更新)
嗯,怎么说数据结构果然很玄妙。按照能不能存储多行元素大致分为两类。 不能存好几行的数据包括pair,int,float,double,char,struct; 能存好几行的:map,unordered_map,list,vector,set,string,array。 1. pair “pair” 是 C++ 标准库中的一个模板类,它用于存储…...
nginx部署vue后显示500 Internal Server Error解决方案
前言 描述:当我配置好全部之后,通过 服务器 ip 地址访问,遇到报错信息:500 Internal Server Error。 今天部署vue前端项目一直报错500,无法显示出主页面。 一个以为是自己的dist位置没有访问正确或者nginx.conf的位…...

微调大型语言模型(一):为什么要微调(Why finetune)?
今天我们来学习Deeplearning.ai的在线课程 微调大型语言模型(一)的第一课:为什么要微调(Why finetune)。 我们知道像GPT-3.5这样的大型语言模型(LLM)它所学到的知识截止到2021年9月,那么如果我们向ChatGPT询问2022年以后发生的事情,它可能会…...

【GO】网络请求例子
post请求;multipart/form-data类型 // 构建请求参数requestData : map[string]interface{}{"gb": "","code": "","reMemberInfo": map[string]interface{}{"shi": "","…...

泡泡玛特海外布局动作不断,开启东南亚潮玩盛会
近日,泡泡玛特海外布局动作不断,9月8日至10日,泡泡玛特2023 PTS潮流玩具展(下简称新加坡PTS)在新加坡滨海湾金沙成功举办,现场人气爆棚,三天吸引了超过2万观众入场,这也是泡泡玛特首…...
uniappAndroid平台签名证书(.keystore)生成
一、安装JRE环境 https://www.oracle.com/java/technologies/downloads/#java8 记住下载默认安装地址。ps:我都默认安装地址C:\Program Files\Java\jdk-1.8 二、安装成功后配置环境变量 系统变量配置 AVA_HOME 放到环境变量去 %JAVA_HOME%\bin 三、生成签名证书…...
Gateway学习和源码解析
文章目录 什么是网关?搭建实验项目demo-servicegateway-service尝试简单上手 路由(Route)断言(Predicate)和断言工厂(Predicate Factory)gateway自带的断言工厂After(请求必须在某个…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
