【C++】搜索二叉树底层实现
目录
一,概念
二,实现分析
1. 插入
(1.)非递归版本
(2.)递归版本
2. 打印搜索二叉树
3.查找函数
(1.)非递归版本
(2.)递归版本
4. 删除函数(重难点)
易错点分析,包你学会
(1.)删除目标,没有左右孩子
(2.)删除目标,只有一个孩子
(3.)删除目标,有两个孩子
代码
(1.)非递归版本
(2.)递归版本
5. 析构函数
6.拷贝构造
三,应用
四,搜索二叉树的缺陷及优化
五,代码汇总
结语

一,概念
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树

为啥又被称作二叉排序树呢? 当该树被层序遍历时,就是升序。
二,实现分析
实验例子:

int a[] = {8, 3, 1, 10, 6, 4, 5, 7, 14, 13};
1. 插入
(1.)非递归版本
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。b、最多查找高度次,走到到空,还没找到,这个值不存在。
比较简单这里就直接放代码:
template <class K>
class BinarySeaTree_node
{typedef BinarySeaTree_node<K> BST_node;
public:BinarySeaTree_node(const K& val): _val(val),_left(nullptr),_right(nullptr){}K _val;BST_node* _left;BST_node* _right;
};template <class T>
class BSTree
{typedef BinarySeaTree_node<T> BST_node;
private:BST_node* root = nullptr;public:bool Insert(const T& val){BST_node* key = new BST_node(val);BST_node* cur = root;BST_node* parent = nullptr;while (cur){if (key->_val < cur->_val){parent = cur;cur = cur->_left;}else if (key->_val > cur->_val){parent = cur;cur = cur->_right;}else{return 0;}}// 查询好位置后,建立链接if (!root){root = key;return 0;}if (key->_val > parent->_val){parent->_right = key;}else{parent->_left = key;}return 1;}
};
(2.)递归版本
这里面整了个活,大家注意了!!!
bool Re_Insert(const T& val){ return Re_Insert_table(root, val);}bool Re_Insert_table(BST_node*& node, const T& val){if (node == nullptr){node = new BST_node(val);return 1;}if (val < node->_left){return Re_Insert_table(node->_left, val);}else if (val > node->_right){ return Re_Insert_table(node->_right, val);}else{return 0;}}这里方便大家理解,我给大家花一个递归展开图。
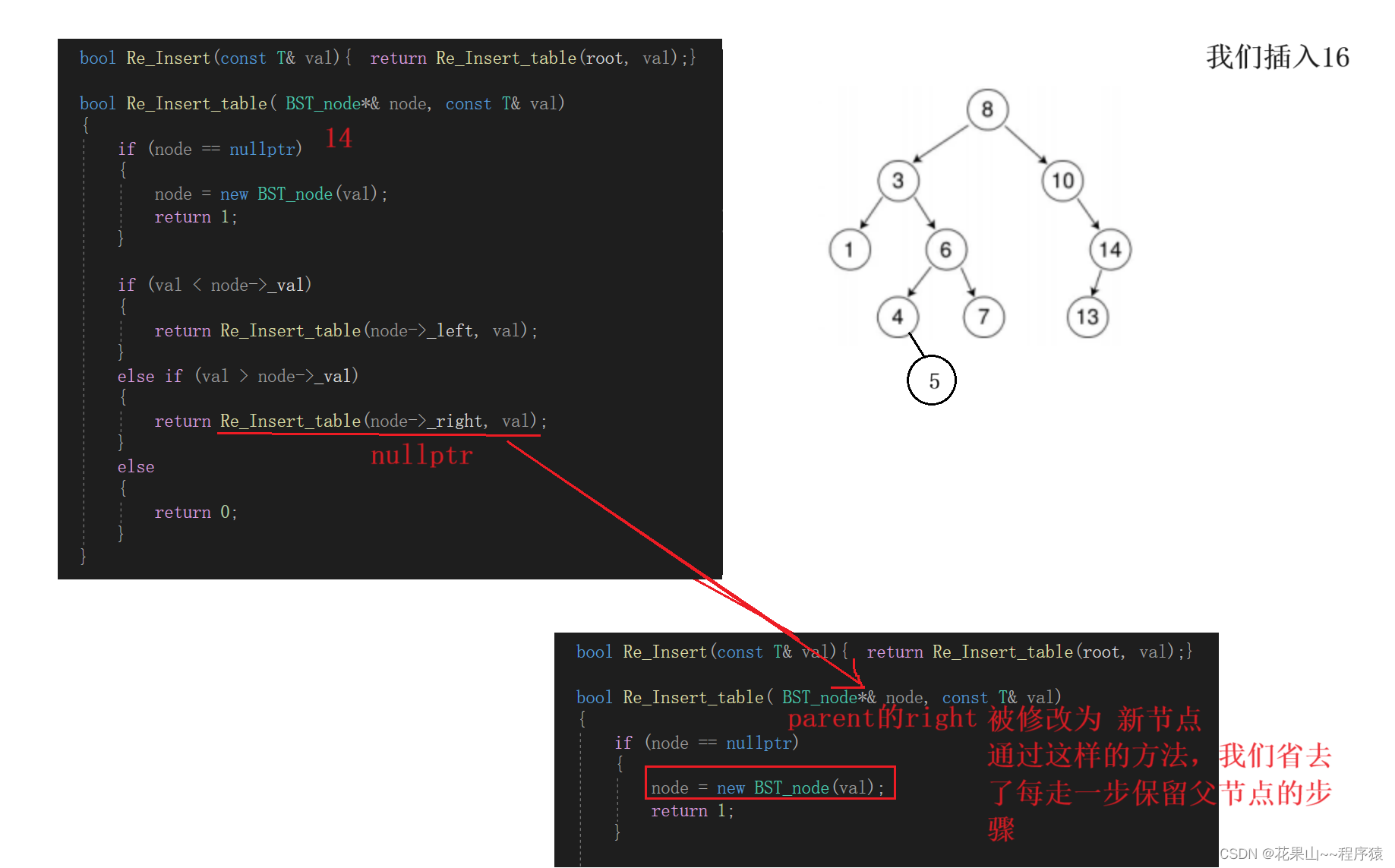
2. 打印搜索二叉树

a. 树为空,则直接新增节点,赋值给root指针b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
这里也是仅做代码分享:
void Print_table() { Re_Print(root); }void Re_Print(const BST_node* node){if (node == nullptr)return;Re_Print(node->_left);cout << node->_val << " ";Re_Print(node->_right);}
3.查找函数
思路:其实也没啥思路,比父结点小,就找左边,否则找右边。
(1.)非递归版本
BST_node* Find(const T& val){//直接跟寻找位置一样BST_node* parent = nullptr;BST_node* cur = root; // 以返回cur的方式返回while (cur) // 非递归版本{if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{return cur;}}return cur;}(2.)递归版本
BST_node* Re_Find(const T& val){ return Re_Find_table(root, val); }BST_node* Re_Find_table(BST_node* node, const T& val){if (node == nullptr)return nullptr;if (val < node->_val){return Re_Find_table(node->_left, val);}else if (val > node->_val){return Re_Find_table(node->_right, val);}else{return node;}}4. 删除函数(重难点)
我们简单寻找了一下思路,如下:
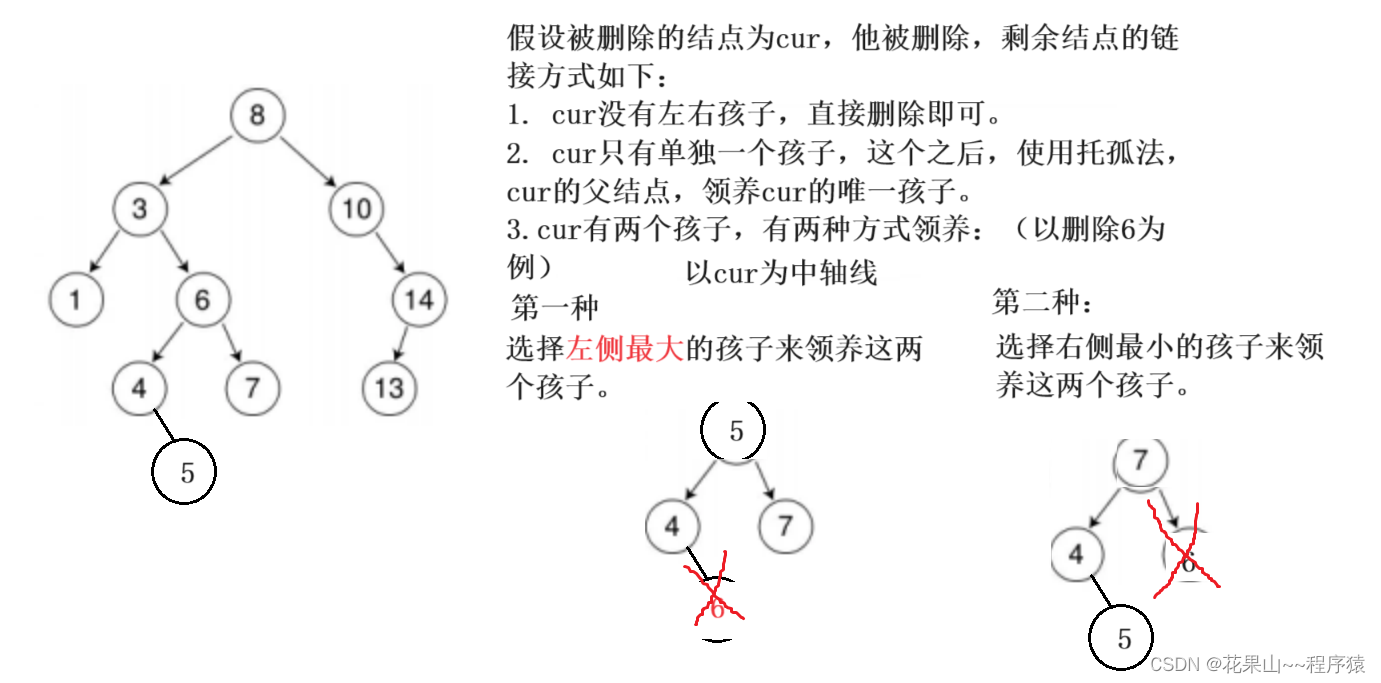
但这些思路只是大概方向,其中藏着许多的坑点,诺接下来我来带大家,对这些易错点进行分析。
首先是查询到目标:
这个比较简单,这里不做解释。
//首先寻找到目标,并且记录到parentBST_node* parent = nullptr;BST_node* cur = root;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{break;}}if (!cur){return 0;}易错点分析,包你学会
(1.)删除目标,没有左右孩子

(2.)删除目标,只有一个孩子
一般的思路:
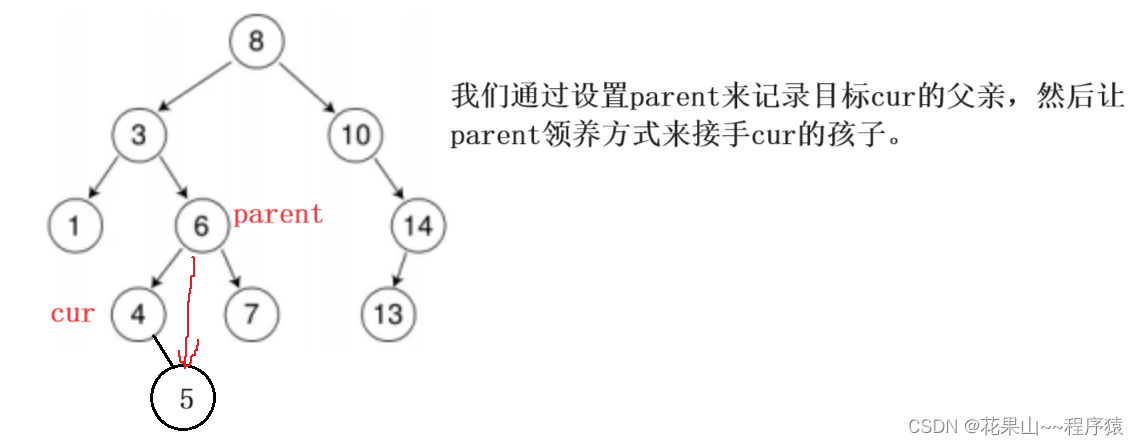 但,这是有漏洞的!
但,这是有漏洞的!
诺:
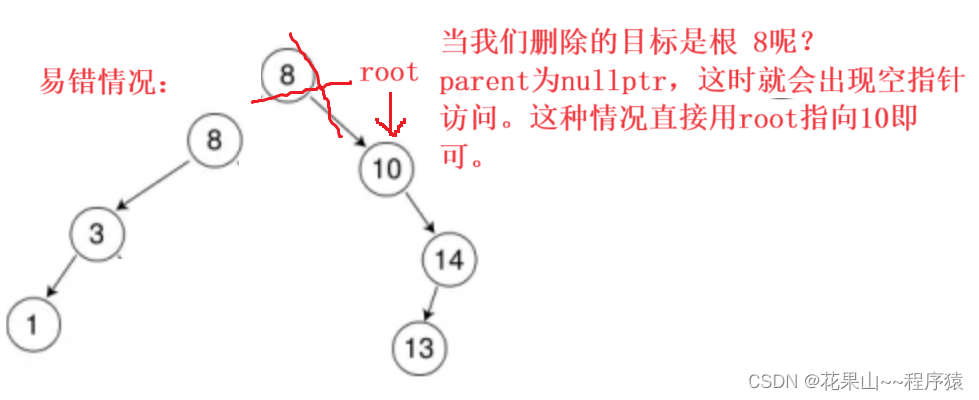
(3.)删除目标,有两个孩子
好啦,前菜上完了来看看,本次的大菜。

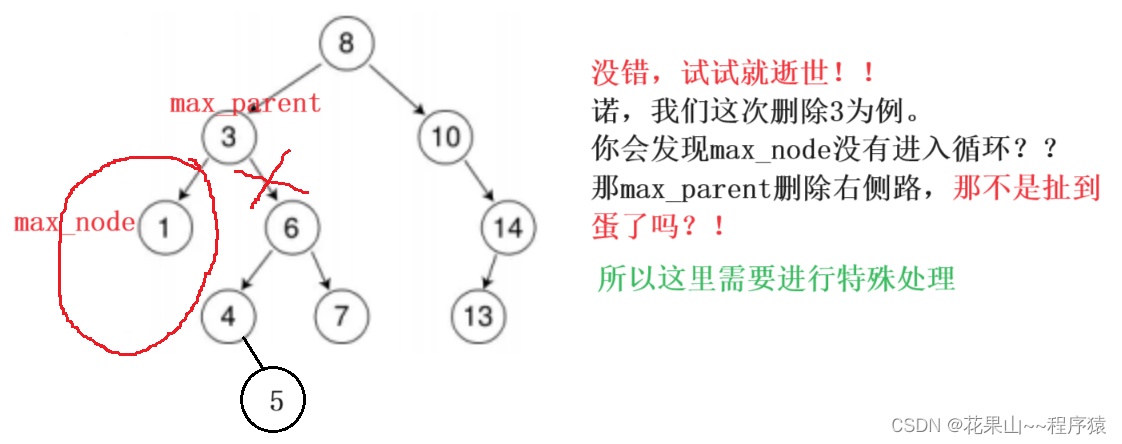
代码
(1.)非递归版本
bool Erase(const T& val){//首先寻找到指定值,并且记录到parentBST_node* parent = nullptr;BST_node* cur = root;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{break;}}if (!cur){return 0;}// 查询成功,开始删除if (!cur->_left && !cur->_right) // cur没有左右孩子{ // 当要删除目标是根if (cur == root){root = nullptr;delete cur;}// 判断cur是左右孩子else if (cur->_val < parent->_val){parent->_left = nullptr;delete cur;}else{parent->_right = nullptr;delete cur;}return 1;}else if (!cur->_left || !cur->_right) // 只有一个孩子{if (!parent) // 判断是否是目标是根{root = cur->_left != nullptr ? cur->_left : cur->_right;delete cur;}// 判断cur为啥孩子else if (cur->_val < parent->_val) // 左侧{parent->_left = cur->_left != nullptr ? cur->_left : cur->_right;delete cur;}else // 右侧{parent->_right = cur->_left != nullptr ? cur->_left : cur->_right;delete cur;}}else // 有2个孩子{ // 使用左侧最大的孩子来领养// 寻找左侧最大BST_node* maxnode = cur->_left;BST_node* max_parent = cur;while (maxnode->_right){max_parent = maxnode;maxnode = maxnode->_right;}// 现在又进入一种特殊情况,1.max_parent就没进入循环,2.进入了循环if (max_parent == cur){max_parent->_left = maxnode->_left;}else{max_parent->_right = maxnode->_left;}// 值转移cur->_val = maxnode->_val;delete maxnode;}return 1;}(2.)递归版本
bool Re_Erease( const T& val){return Re_Erease_table(root, val);}bool Re_Erease_table(BST_node*& node, const T& val){// 首先我们先找到值if (node == nullptr){return 0; // 如果访问到了空,则说明删除失败,原因是:不存在}if (val < node->_val){return Re_Erease_table(node->_left, val);}else if (val > node->_val){return Re_Erease_table(node->_right, val);}else{// 开始删除目标数据。方法如下;// 1. 就按照非递归的思路,不用改多少代码 // 2. 使用递归方法,优势就是代码简洁// 这里使用方法2BST_node* del = node; // 保存每次访问的对象,如果是目标,就备份好了if (node->_left == nullptr){node = node->_right;}else if (node->_right == nullptr){node = node->_left;}else{//处理左右都有孩子的目标// 左侧查找最大值,右侧查找最小值BST_node* max_node = node->_left;while (max_node->_right){max_node = max_node->_right;}// 完成循环后,max_node最多有左孩子,然后数据交换,我们以目标左侧树为起点// 再次递归删除替换数据。swap(max_node->_val, node->_val);return Re_Erease_table(node->_left, val); //已经完成删除,就直接退出,以免触发删除delete} //处理前两种情况delete del;}}5. 析构函数
思路:
~BSTree(){ Distroy_Re(root);root = nullptr; }
void Distroy_Re(BST_node*& node) // 我们采用递归删除{if (node == nullptr)return ;// 先处理左右孩子Distroy_Re(node->_left);Distroy_Re(node->_right);delete node;node = nullptr;}6.拷贝构造

// 我们实现了拷贝构造,默认构造函数则不会生成 // 解决方案:1.实现构造函数 2.使用default关键字,强制生成默认构造BSTree() {}// BSTree() = defaultBSTree(const BSTree& Tree) // 拷贝构造{root = copy(Tree.root);}BST_node* copy(BST_node* root){if (root == nullptr)return nullptr;BST_node* new_node = new BST_node(root->_val);new_node->_left = copy(root->_left);new_node->_right = copy(root->_right);return new_node;}三,应用
四,搜索二叉树的缺陷及优化
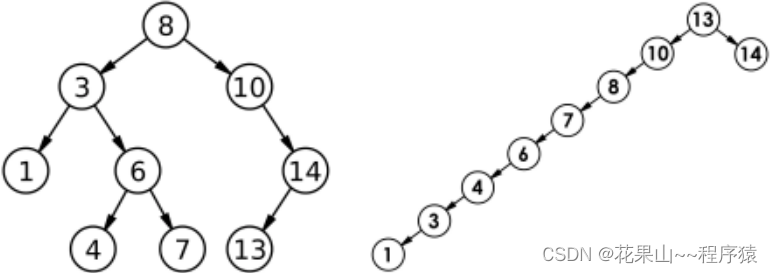
最坏情况:N
平均情况:O(logN)
五,代码汇总
namespace key
{
template <class K>
class BinarySeaTree_node
{typedef BinarySeaTree_node<K> BST_node;
public:BinarySeaTree_node(const K& val): _val(val),_left(nullptr),_right(nullptr){}K _val;BST_node* _left;BST_node* _right;
};template <class T>
class BSTree
{
public:typedef BinarySeaTree_node<T> BST_node;// 我们实现了拷贝构造,默认构造函数则不会生成 // 解决方案:1.实现构造函数 2.使用default关键字,强制生成默认构造BSTree(){}// BSTree() = defaultBSTree(const BSTree& Tree) // 拷贝构造{root = copy(Tree.root);}BSTree<T>& operator=(BSTree<T> t){swap(root, t.root);return *this;}BST_node* copy(BST_node* root){if (root == nullptr)return nullptr;BST_node* new_node = new BST_node(root->_val);new_node->_left = copy(root->_left);new_node->_right = copy(root->_right);return new_node;}bool Re_Insert(const T& val) { return Re_Insert_table(root, val); }void Re_Print() { Re_Print_table(root); }bool Re_Erease(const T& val) { return Re_Erease_table(root, val); }BST_node* Re_Find(const T& val) { return Re_Find_table(root, val); }bool Insert(const T& val){BST_node* key = new BST_node(val);BST_node* cur = root;BST_node* parent = nullptr;while (cur){if (key->_val < cur->_val){parent = cur;cur = cur->_left;}else if (key->_val > cur->_val){parent = cur;cur = cur->_right;}else{return 0;}}// 查询好位置后,建立链接if (!root){root = key;return 0;}if (key->_val > parent->_val){parent->_right = key;}else{parent->_left = key;}return 1;}BST_node* Find(const T& val){//直接跟寻找位置一样BST_node* parent = nullptr;BST_node* cur = root; // 以返回cur的方式返回while (cur) // 非递归版本{if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{return cur;}}return cur;}bool Erase(const T& val){//首先寻找到指定值,并且记录到parentBST_node* parent = nullptr;BST_node* cur = root;while (cur){if (val < cur->_val){parent = cur;cur = cur->_left;}else if (val > cur->_val){parent = cur;cur = cur->_right;}else{break;}}if (!cur){return 0;}// 查询成功,开始删除if (!cur->_left && !cur->_right) // cur没有左右孩子{ // 当要删除目标是根if (cur == root){root = nullptr;delete cur;}// 判断cur是左右孩子else if (cur->_val < parent->_val){parent->_left = nullptr;delete cur;}else{parent->_right = nullptr;delete cur;}return 1;}else if (!cur->_left || !cur->_right) // 只有一个孩子{if (!parent) // 判断是否是目标是根{root = cur->_left != nullptr ? cur->_left : cur->_right;delete cur;}// 判断cur为啥孩子else if (cur->_val < parent->_val) // 左侧{parent->_left = cur->_left != nullptr ? cur->_left : cur->_right;delete cur;}else // 右侧{parent->_right = cur->_left != nullptr ? cur->_left : cur->_right;delete cur;}}else // 有2个孩子{ // 使用左侧最大的孩子来领养// 寻找左侧最大BST_node* maxnode = cur->_left;BST_node* max_parent = cur;while (maxnode->_right){max_parent = maxnode;maxnode = maxnode->_right;}// 现在又进入一种特殊情况,1.max_parent就没进入循环,2.进入了循环if (max_parent == cur){max_parent->_left = maxnode->_left;}else{max_parent->_right = maxnode->_left;}// 值转移cur->_val = maxnode->_val;delete maxnode;}return 1;}~BSTree(){Distroy_Re(root);root = nullptr;}protected:bool Re_Insert_table(BST_node*& node, const T& val){if (node == nullptr){node = new BST_node(val);return 1;}if (val < node->_val){return Re_Insert_table(node->_left, val);}else if (val > node->_val){return Re_Insert_table(node->_right, val);}else{return 0;}}void Re_Print_table(const BST_node* node){if (node == nullptr)return;Re_Print_table(node->_left);cout << node->_val << " ";Re_Print_table(node->_right);}BST_node* Re_Find_table(BST_node* node, const T& val){if (node == nullptr)return nullptr;if (val < node->_val){return Re_Find_table(node->_left, val);}else if (val > node->_val){return Re_Find_table(node->_right, val);}else{return node;}}bool Re_Erease_table(BST_node*& node, const T& val){// 首先我们先找到值if (node == nullptr){return 0; // 如果访问到了空,则说明删除失败,原因是:不存在}if (val < node->_val){return Re_Erease_table(node->_left, val);}else if (val > node->_val){return Re_Erease_table(node->_right, val);}else{// 开始删除目标数据。方法如下;// 1. 就按照非递归的思路,不用改多少代码 // 2. 使用递归方法,优势就是代码简洁// 这里使用方法2BST_node* del = node; // 保存每次访问的对象,如果是目标,就备份好了if (node->_left == nullptr){node = node->_right;}else if (node->_right == nullptr){node = node->_left;}else{//处理左右都有孩子的目标// 左侧查找最大值,右侧查找最小值BST_node* max_node = node->_left;while (max_node->_right){max_node = max_node->_right;}// 完成循环后,max_node最多有左孩子,然后数据交换,我们以目标左侧树为起点// 再次递归删除替换数据。swap(max_node->_val, node->_val);return Re_Erease_table(node->_left, val); //已经完成删除,就直接退出,以免触发删除delete}// 查找到删除数据delete del;}}void Distroy_Re(BST_node*& node) // 我们采用递归删除{if (node == nullptr)return;// 先处理左右孩子Distroy_Re(node->_left);Distroy_Re(node->_right);delete node;node = nullptr;}
private:BST_node* root = nullptr;};
}结语
本小节就到这里了,感谢小伙伴的浏览,如果有什么建议,欢迎在评论区评论,如果给小伙伴带来一些收获请留下你的小赞,你的点赞和关注将会成为博主创作的动力
相关文章:

【C++】搜索二叉树底层实现
目录 一,概念 二,实现分析 1. 插入 (1.)非递归版本 (2.)递归版本 2. 打印搜索二叉树 3.查找函数 (1.)非递归版本 (2.)递归版本 4. 删除函数&#x…...

C8051F020 SMBus一直处于busy状态解决办法
当SMBus总线处于busy状态切且无法自动释放时,SMB0CN寄存器的第7位一直为 1,总线没有释放。 SMBus总线释放超时的一个纠错机制,它允许SMBus状态机在 SDA 和 SCL 信号线同为高电平超过 10个SMBus时钟源周期后判断总线为释放状态。 如果总线释放…...

Activiz 9.2 for Linux Crack
Activiz 9.2 在 C#、.Net 和 Unity 软件中为您的 3D 内容释放可视化工具包的强大功能。 ActiViz 允许您轻松地将 3D 可视化集成到您的应用程序中。 ActiViz 功能 用 C# 封装的 3D 可视化软件系统 允许在 .NET 环境中快速开发可投入生产的交互式3D 应用程序 支持窗口演示基础 (…...

数据结构 - 链表
线性表的链式存储结构 概念 将线性表 L (a0, a1, … , an-1)中各元素分布在存储器的不同存储块,成为结点,通过地址或指针建立元素之间的联系。 结点的 data 域存放数据元素 ai ,而 next 域是一个指针,指向 ai 的直接后继 ai1 …...

Android 12 Bluetooth源码分析蓝牙配对
本文主要是列出一些蓝牙配对重要的类和方法/函数,遇到相关问题时方便查找添加log排查。 蓝牙扫描列表页面:packages/apps/Settings/src/com/android/settings/bluetooth/DeviceListPreferenceFragment.java点击其中一个设备会调用:onPrefere…...
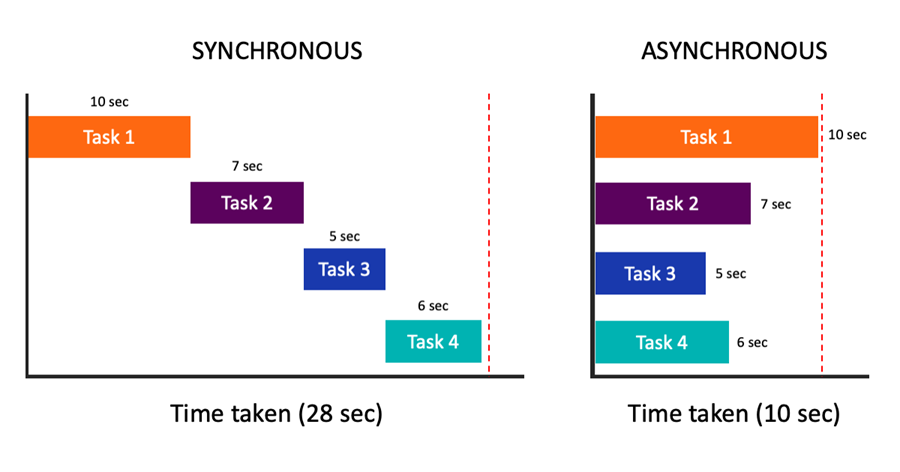
Python异步编程并发执行爬虫任务,用回调函数解析响应
一、问题:当发送API请求,读写数据库任务较重时,程序运行效率急剧下降。 异步技术是Python编程中对提升性能非常重要的一项技术。在实际应用,经常面临对外发送网络请求,调用外部接口,或者不断更新数据库或文…...

React组件化开发
1.组件的定义方式 函数组件Functional Component类组件Class Component 2.类组件 export class Profile extends Component {render() {console.log(this.context);return (<div>Profile</div>)} } 组件的名称是大写字符开头(无论类组件还是函数组件…...
--crypto - 加解密和hash函数)
LuatOS-SOC接口文档(air780E)--crypto - 加解密和hash函数
crypto.md5(str) 计算md5值 参数 传入值类型 解释 string 需要计算的字符串 返回值 返回值类型 解释 string 计算得出的md5值的hex字符串 例子 -- 计算字符串"abc"的md5 log.info("md5", crypto.md5("abc"))crypto.hmac_md5(str, k…...

自动化测试的定位及一些思考
大家对自动化的理解,首先是想到Web UI自动化,这就为什么我一说自动化,公司一般就会有很多人反对,因为自动化的成本实在太高了,其实自动化是分为三个层面的(UI层自动化、接口自动化、单元测试)&a…...
展会动态 | 迪捷软件邀您参加2023世界智能网联汽车大会
*9月18日之前注册的观众免收门票费* 由北京市人民政府、工业和信息化部、公安部、交通运输部和中国科学技术协会联合主办的2023世界智能网联汽车大会将于9月21日-24日在北京中国国际展览中心(顺义馆)举行。 论坛背景 本届展会以“聚智成势 协同向新——…...

jenkins自动化部署springboot、gitee项目
服务器需要安装jdk11、maven、gitee 1. jenkins安装 # yum源 sudo wget -O /etc/yum.repos.d/jenkins.repo https://pkg.jenkins.io/redhat/jenkins.repo # 公钥 sudo rpm --import https://pkg.jenkins.io/redhat/jenkins.io-2023.key # 安装 yum install jenkins如果yum源报…...
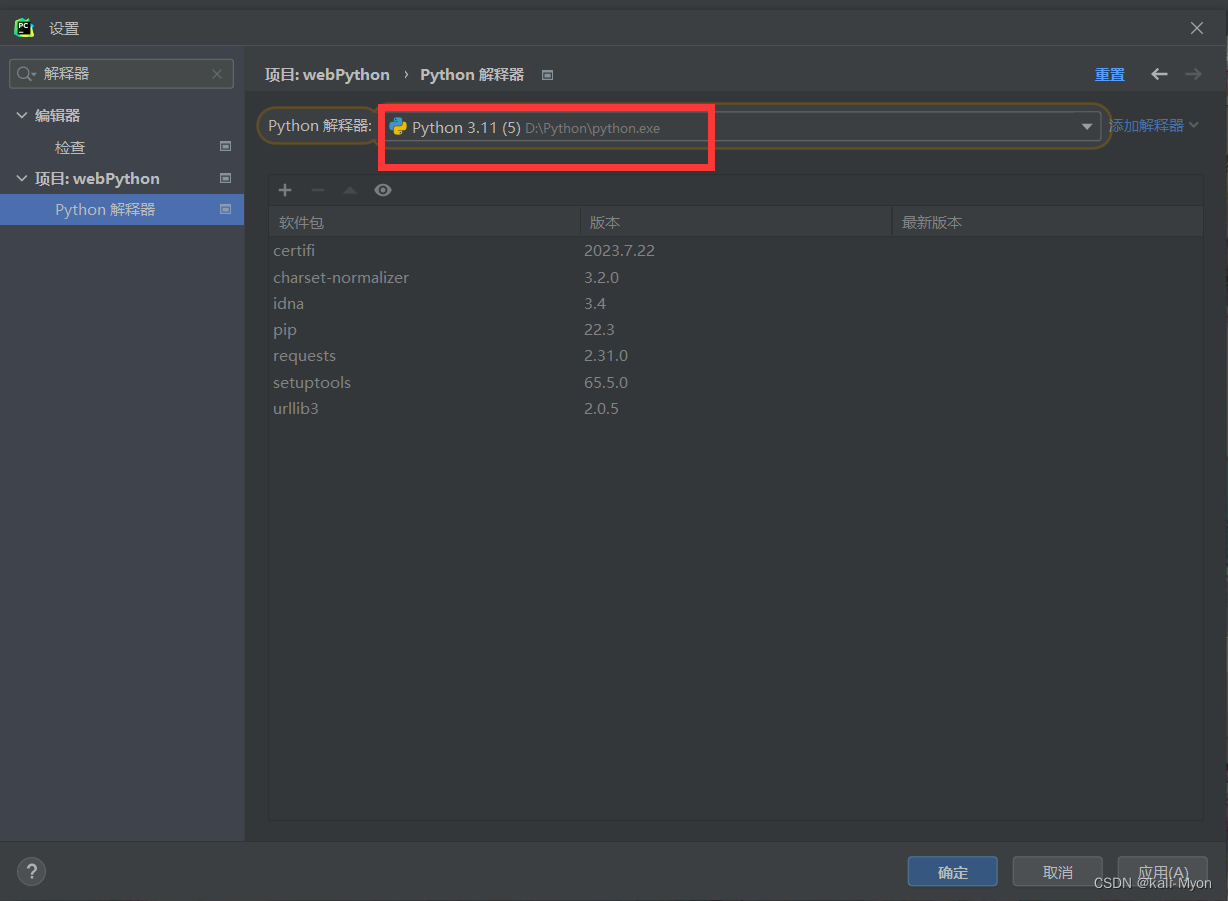
Python环境配置及基础用法Pycharm库安装与背景设置及避免Venv文件夹
目录 一、Python环境部署及简单使用 1、Python下载安装 2、环境变量配置 3、检查是否安装成功 4、Python的两种模式(编辑模式&交互模式) 二、Pycharm库安装与背景设置 1、Python库安装 2、Pycharm自定义背景 三、如何避免Venv文件夹 一、P…...

PHP常见的SQL防注入方法
利用Mysqli和PDO 产生原因主要就是一些数据没有经过严格的验证,然后直接拼接 SQL 去查询。导致产生漏洞,比如: $id $_GET[id]; $sql "SELECT name FROM users WHERE id $id";因为没有对 $_GET[‘id’] 做数据类型验证…...

分布式和中间件等
raft协议 paxos算法ddos 如何避免?怎么预防?怎么发现?利用了TCP什么特点?怎么改进TCP可以预防?服务端处理不了的请求怎么办?连接数最大值需要设置吗?怎么设置? Thrift RPC过程是什么样子的?异构系统怎么完成通信?跟http相比什么优缺点?了解grpc吗?kafka topic part…...
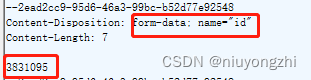
通过http发送post请求的三种Content-Type分析
通过okhttp向服务端发起post网络请求,可以通过Content-Type设置发送请求数据的格式。 常用到的三种: 1)application/x-www-form-urlencoded; charsetutf-8 2)application/json; charsetutf-8 3)multipart/form-dat…...
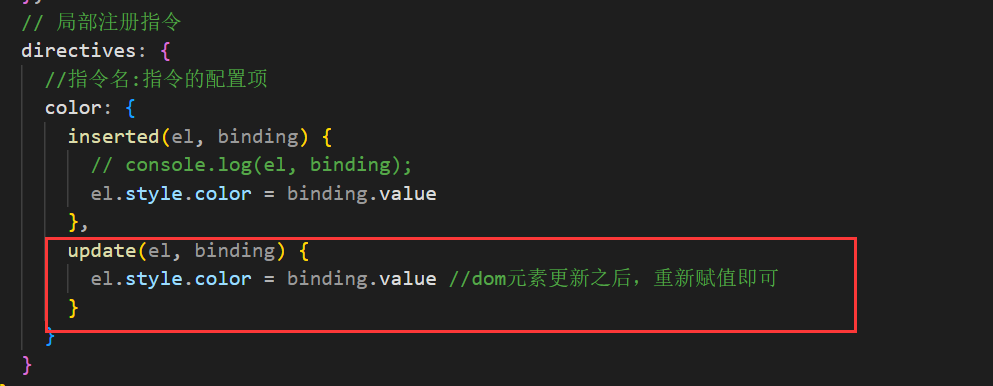
Vue中的自定义指令详解
文章目录 自定义指令自定义指令-指令的值(给自定义指令传参数) 自定义指令 自定义指令:自己定义的指令,可以封装一些dom 操作,扩展额外功能(自动聚焦,自动加载,懒加载等复杂的指令封…...

[管理与领导-100]:管理者到底是什么?调度器?路由器?交换机?监控器?
目录 前言: 二层交换机 三层路由器 监视器(Monitor) 调度器 前言: 人在群体中,有点像设备在网络中,管理者到底承担什么的功能? 二层交换机 交换机是计算机网络中,用于连接多台…...

保研CS/软件工程/通信问题汇总
机器学习 1.TP、TN、FP、FN、F1 2.机器学习和深度学习的区别和联系 模型复杂性:深度学习是机器学习的一个子领域,其主要区别在于使用深层的神经网络模型。深度学习模型通常包含多个隐层,可以学习更加复杂的特征表示,因此在某些任…...

word、excel、ppt转为PDF
相关引用对象在代码里了 相关依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi-ooxml</artifactId><version>4.0.1</version></dependency> <dependency><groupId>org.apache.poi</group…...
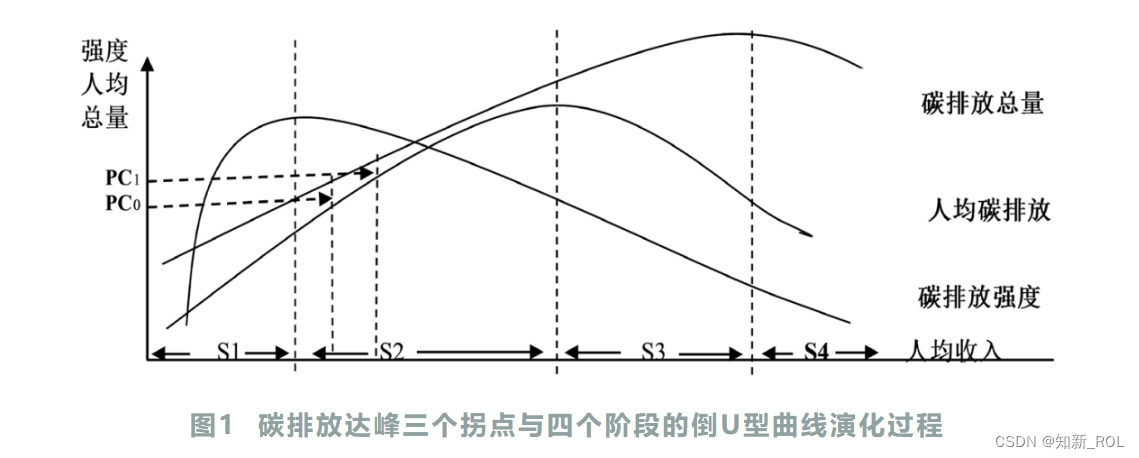
2023华为杯D题——基于Kaya模型的碳排放达峰实证研究
一、前言 化石能源是推动现代经济增长的重要生产要素,经济生产活动与碳排放活动密切相关。充分认识经济增长与碳排放之间的关系对转变生产方式,确定碳达峰、碳中和路径极为必要。本研究在对经济增长与碳排放关系现有研究梳理的基础上,系统地分…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
