博弈论——连续产量古诺模型
连续产量古诺模型
连续产量古诺模型是博弈论中非常经典的模型,以两厂商连续产量古诺博弈为例:
1、模型建立
Player:两个供应相同产品的厂商
产量:厂商1的产量为q1,厂商2的产量为q2,市场总供给为Q=q1+q2。
市场出清价格P:市场总供给的函数P(Q)=8-Q (市场出清价格是可以将产品全部卖出的价格)
成本:设两个厂商都无固定成本,每增加一单位产量的边际成本c1=c2=c。
最后强调两个厂商同时决策,即决策之前都不知道另一方产量(完全信息静态博弈)。
该博弈两博弈方的策略空间是他们可以选择的产量。假设产量是连续变量,也就是说两厂商有无限多种可选策略。两博弈方的得益是两个厂商各自的利润,即各自的销售收益减去各自的成本:
π 1 = q 1 P ( Q ) − q 1 c = q 1 ( 8 − ( q 1 + q 2 ) ) − c q 1 = − q 1 2 − c q 1 − q 1 q 2 + 8 q 1 π_1=q_1 P(Q)-q_1 c=q_1 (8-(q_1+q_2 ))-cq_1=-q_1^2-cq_1-q_1 q_2+8q_1 π1=q1P(Q)−q1c=q1(8−(q1+q2))−cq1=−q12−cq1−q1q2+8q1
和
π 2 = q 2 P ( Q ) − q 2 c = q 2 ( 8 − ( q 1 + q 2 ) ) − c q 2 = − q 2 2 − c q 2 − q 1 q 2 + 8 q 2 π_2=q_2 P(Q)-q_2 c=q_2 (8-(q_1+q_2 ))-cq_2=-q_2^2-cq_2-q_1 q_2+8q_2 π2=q2P(Q)−q2c=q2(8−(q1+q2))−cq2=−q22−cq2−q1q2+8q2
其中, π 1 π_1 π1、 π 2 π_2 π2分别是厂商1、厂商2的利润。可以看出,两博弈方的得益都取决于双方的产量。这个博弈中,我们需要找到纳什均衡,即只要策略组合 ( q 1 ∗ , q 2 ∗ ) (q_1^*,q_2^*) (q1∗,q2∗)满足 q 1 ∗ q_1^* q1∗和 q 2 ∗ q_2^* q2∗相互是对于对方的最佳对策就构成纳什均衡。
根据纳什均衡的定义知道,纳什均衡就是相互是最优对策的各博弈方策略组合。因此,如果策略组合 ( q 1 ∗ , q 2 ∗ ) (q_1^*,q_2^*) (q1∗,q2∗)是本博弈的纳什均衡,就必须是下列最大值问题的解:
{ m a x q 1 ( − q 1 2 − c q 1 − q 1 q 2 ∗ + 8 q 1 ) m a x q 2 ( − q 2 2 − c q 2 − q 1 ∗ q 2 + 8 q 2 ) \begin{cases} \underset{q_1}{max}(-q_1^2-cq_1-q_1 q_2^*+8q_1)\\ \underset{q_2}{max}(-q_2^2-cq_2-q_1^* q_2+8q_2) \end{cases} ⎩ ⎨ ⎧q1max(−q12−cq1−q1q2∗+8q1)q2max(−q22−cq2−q1∗q2+8q2)
2、模型求解
上述两个求最大值的式子都是各自变量的二次式,且二次项系数都小于0,因此只要 q 1 ∗ q_1^* q1∗和 q 2 ∗ q_2^* q2∗能使两式各自对 q 1 q_1 q1和 q 2 q_2 q2的导数为0就能实现两式的最大值。
即令
{ − 2 q 1 − c − q 2 ∗ + 8 = 0 − 2 q 2 − c − q 1 ∗ + 8 = 0 \begin{cases} -2q_1-c-q_2^*+8=0\\ -2q_2-c-q_1^*+8=0 \end{cases} {−2q1−c−q2∗+8=0−2q2−c−q1∗+8=0
又因为策略组合 ( q 1 ∗ , q 2 ∗ ) (q_1^*,q_2^*) (q1∗,q2∗)是本博弈的纳什均衡,故解下列方程
{ − 2 q 1 ∗ − c − q 2 ∗ + 8 = 0 − 2 q 2 ∗ − c − q 1 ∗ + 8 = 0 \begin{cases} -2q_1^*-c-q_2^*+8=0\\ -2q_2^*-c-q_1^*+8=0 \end{cases} {−2q1∗−c−q2∗+8=0−2q2∗−c−q1∗+8=0
得到方程组唯一解:
{ q 1 ∗ = 8 − c 3 q 2 ∗ = 8 − c 3 \begin{cases} q_1^*=\frac {8-c}{3}\\ q_2^*=\frac {8-c}{3} \end{cases} {q1∗=38−cq2∗=38−c
可以进一步得到市场总供给
Q = q 1 ∗ + q 2 ∗ = 16 − 2 c 3 Q=q_1^*+q_2^*=\frac {16-2c}{3} Q=q1∗+q2∗=316−2c
市场出清价格为
P = 8 − ( 16 − 2 c ) / 3 = 8 + 2 c 3 P=8-(16-2c)/3=\frac {8+2c}{3} P=8−(16−2c)/3=38+2c
故双方的得益分别为:
π 1 = q 1 ∗ P ( Q ) − q 1 ∗ c = 8 − c 3 ∙ ( 8 + 2 c 3 − c ) = ( 8 − c ) 2 9 π_1=q_1^* P(Q)-q_1^* c=\frac {8-c}{3}∙(\frac {8+2c}{3}-c)=\frac{(8-c)^2}{9} π1=q1∗P(Q)−q1∗c=38−c∙(38+2c−c)=9(8−c)2
π 2 = q 2 ∗ P ( Q ) − q 2 ∗ c = 8 − c 3 ∙ ( 8 + 2 c 3 − c ) = ( 8 − c ) 2 9 π_2=q_2^* P(Q)-q_2^* c=\frac {8-c}{3}∙(\frac {8+2c}{3}-c)=\frac{(8-c)^2}{9} π2=q2∗P(Q)−q2∗c=38−c∙(38+2c−c)=9(8−c)2
总收益为(s为separate):
π s ∗ = π 1 + π 2 = 2 ( 8 − c ) 2 9 π_s^*=π_1+π_2=\frac{2(8-c)^2}{9} πs∗=π1+π2=92(8−c)2
π s ∗ π_s^* πs∗为两个厂商在各自做决策场景下的总收益。
3、模型拓展
如果从两个厂商总体利益最大化角度进行统一的产量选择,就要求实现两个厂商总和利润最大的总产量。设总产量为Q,则总利润为
π o = Q P ( Q ) − c Q = Q ( 8 − Q ) − c Q = − Q 2 + ( 8 − c ) Q π_o=QP(Q)-cQ=Q(8-Q)-cQ=-Q^2+(8-c)Q πo=QP(Q)−cQ=Q(8−Q)−cQ=−Q2+(8−c)Q
其中 π o π_o πo(o为overall)为两个厂商总体决策时的总利润,则同样求一阶导得到当 Q = ( 8 − c ) / 2 Q=(8-c)/2 Q=(8−c)/2时,取得最大值
π o ∗ = ( 8 − c ) 2 4 π_o^*=\frac {(8-c)^2}{4} πo∗=4(8−c)2
4、结果比较
将两个厂商进行统一的产量选择时的结果与两个厂商独立决策、追求各自利润最大化时的博弈结果相比:
π ∗ = { 2 ( 8 − c ) 2 9 , Q ∗ = ( 16 − 2 c ) 3 ( 8 − c ) 2 4 , Q ∗ = ( 8 − c ) 2 π^*= \begin{cases} \frac{2(8-c)^2}{9}, Q^*=\frac {(16-2c)}{3} \\ \frac {(8-c)^2}{4} , Q^*=\frac {(8-c)}{2}\\ \end{cases} π∗={92(8−c)2,Q∗=3(16−2c)4(8−c)2,Q∗=2(8−c)
不难发现,从两个厂商总体利益最大化角度进行统一的产量选择时,总产量较小,而总利润却较高。
因此从两个厂商的总体来看,根据总体利益最大化决策效率更高,即如果两个厂商联合起来决定产量,先定出使总利益最大的总产量( 8 − c 2 \frac {8-c}{2} 28−c)后各自生产其一半( 8 − c 4 \frac {8-c}{4} 48−c),则各自可分享到单位利润 ( 8 − c ) 2 8 \frac {(8-c)^2}{8} 8(8−c)2,比各自独立决策获得的利润 ( 8 − c ) 2 9 \frac {(8-c)^2}{9} 9(8−c)2要高。
当然,在两个独立决策的企业之间实现合作并不容易。合作难以实现的原因主要是合作的产量组合( 8 − c 4 \frac {8-c}{4} 48−c, 8 − c 4 \frac {8-c}{4} 48−c)不是纳什均衡。在这个策略组合中,双方都可以独自改变自己的策略得到更高的利润,双方都有突破 8 − c 4 \frac {8-c}{4} 48−c单位产量的冲动。在缺乏有强制性协议保障的情况下,这种冲动注定了不可能维持产量组合( 8 − c 4 \frac {8-c}{4} 48−c, 8 − c 4 \frac {8-c}{4} 48−c),两个厂商早晚都会增产,只有达到纳什均衡产量( 8 − c 3 \frac {8-c}{3} 38−c, 8 − c 3 \frac {8-c}{3} 38−c)后才会稳定下来,因为这时任意一个厂商单独改变产量都不利于自己。如果将遵守还是突破限额作为厂商面临的选择,则构成如下图所示中得益矩阵表示的博弈。不难看出,下图所示是一个囚徒困境。
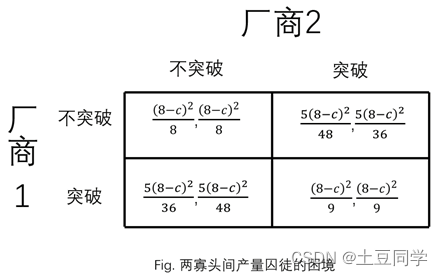
5、总结
上述博弈是根据谢识予老师的《经济博弈论》中连续产量古诺模型改编得到的比较简单版本。更复杂的模型可以包括n个寡头,市场出清价格与市场总产量的函数关系P=P(Q) 可以更复杂,每个厂商的成本也可以变化或不同。但不管这些因素如何变化,分析思路与上述模型是相似的,不过纳什均衡的产量组合将变成n个偏微分为0的联立方程组解。
产量博弈的古诺模型是一种囚徒困境,无法实现博弈方总体和各个博弈方各自最大利益的结论,该博弈说明自由竞争经济同样存在低效率问题,放任自流并非最好的政策。这些结论也说明了,政府对市场调控和监管的必要性。
相关文章:

博弈论——连续产量古诺模型
连续产量古诺模型 连续产量古诺模型是博弈论中非常经典的模型,以两厂商连续产量古诺博弈为例: 1、模型建立 Player:两个供应相同产品的厂商 产量:厂商1的产量为q1,厂商2的产量为q2,市场总供给为Qq1q2。…...

ROS2 驱动思岚G4雷达(ydlidar)- Rviz显示
记录G4雷达的配置 系统环境为:Ubuntu22.04 配置步骤 1、安装雷达SDK 2、构建 G4 雷达 ROS2 项目工程文件 3、使用Rviz可视化界面显示 1、安装雷达SDK 1.1 安装CMake YDLidar SDK需要CMake 2.8.2作为依赖项 Ubuntu 18.04或者Ubuntu 22.04 sudo apt install cmak…...
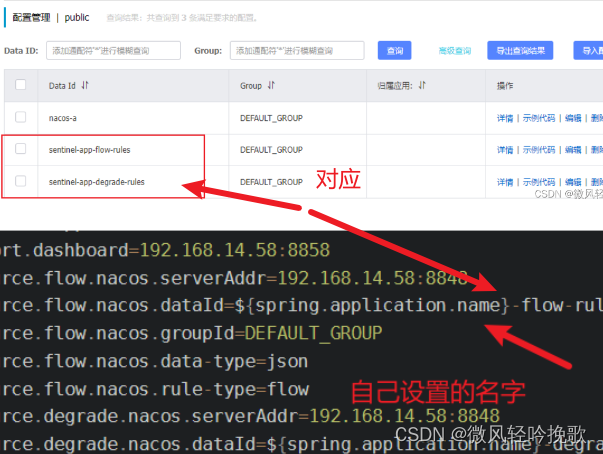
Spring Cloud Alibaba Sentinel流量防卫兵
文章目录 Spring Cloud Alibaba Sentinel流量防卫兵1. 分布式遇到的问题2.解决的方法 Sentinel: 分布式系统的流量防卫兵1. 简介和特折 Sentinel流量防卫兵的搭建1.引入依赖2.添加配置类3.运行类上添加SentinelResource,并配置blockHandler和fallback4. linux中放入…...
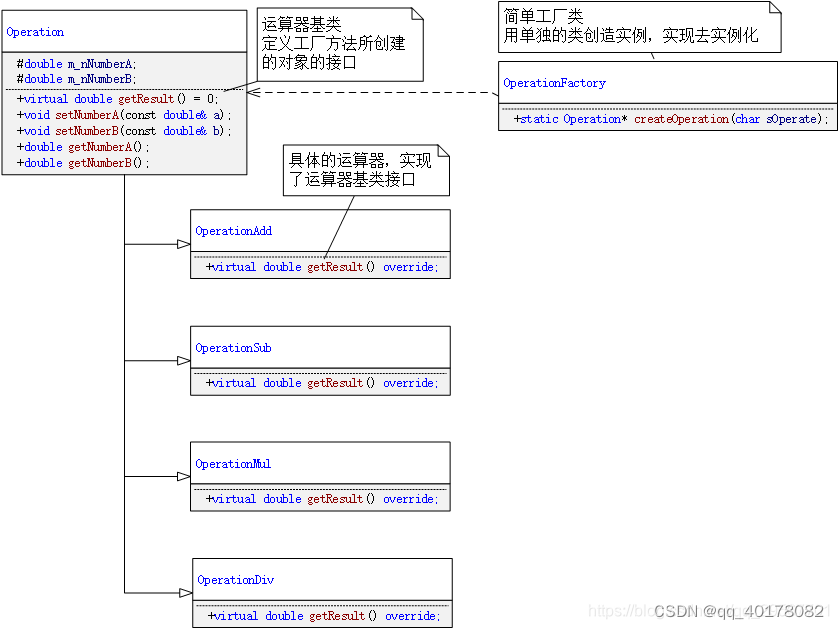
1.简单工厂模式
UML类图 代码 main.cpp #include <iostream> #include "OperationFactory.h" using namespace std;int main(void) {float num1;float num2;char operate;cin >> num1 >> num2 >> operate;Operation* oper OperationFactory::createOpera…...

GitHub Copilot Chat
9月21日,GitHub在官网宣布,所有个人开发者可以使用GitHub Copilot Chat。用户通过文本问答方式就能生成、检查、分析各种代码。 据悉,GitHub Copilot Chat是基于OpenAI的GPT-4模型打造而成,整体使用方法与ChatGPT类似。例如&…...

利用 QT 完成一个人脸识别系统,完成登录操作
1.配置文件 # Project created by QtCreator 2023-09-22T10:34:23 # #-------------------------------------------------QT core guigreaterThan(QT_MAJOR_VERSION, 4): QT widgetsTARGET project TEMPLATE appSOURCES main.cpp\widget.cppHEADERS widget.hFOR…...
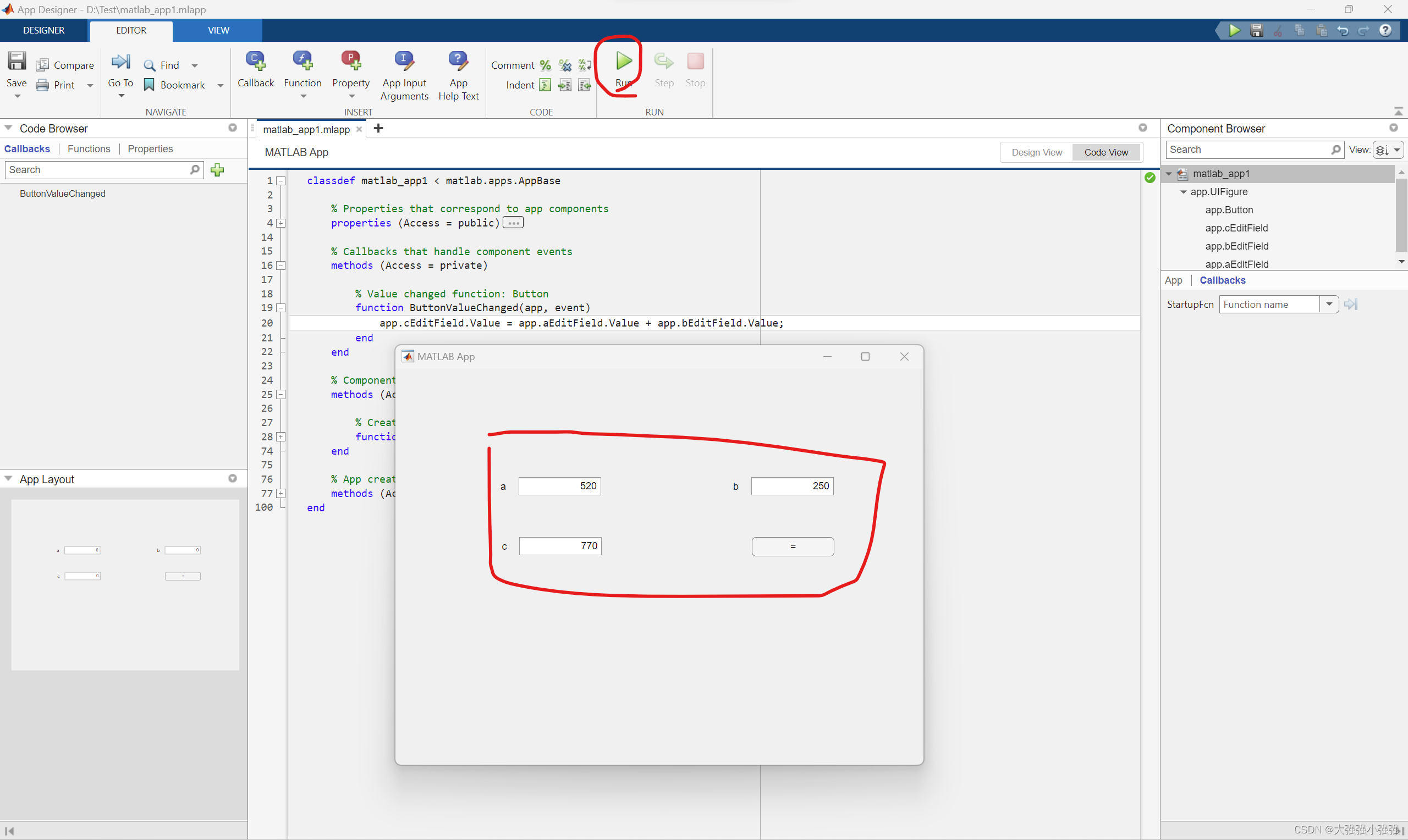
MATLAB APP纯小白入门 两数相加
万事开头难,最怕第一次。使用matlab APP 实现两数求和,如下图所示,c a b,输入数字后,按 “” 就计算。 步骤 拖拽三个 Edit Field(Numeric) 过来,并且双击名字分别改为 a,b,c。注意修改名字后右边会有点变…...
ubuntu右上角的网络连接图标消失解决办法
ubuntu更新了几个文件后,我的ubuntu系统右上角的网络连接图标就消失了,然后怎么也找不到了,怎么办呢? 1、按快捷键ctrlaltt打开终端 2、按以下顺序输入如下的命令行 sudo service network-manager stop sudo rm /var/lib/Netw…...

conda创建虚拟环境安装aix360
目录 创建虚拟环境查看已有虚拟环境进入所创建的虚拟环境查看已安装的程序查看已安装的python模块配置镜像pipconda 安装aix360将环境添加到jupyter删除虚拟环境 创建虚拟环境 conda create -n aix360 python3.9查看已有虚拟环境 conda env list进入所创建的虚拟环境 activa…...

CentOS安装mariadb
1、 安装 [rootlocalhost ~]# yum install mariadb mariadb-server2、 启动并自启 [rootecs-3f21 ~]# systemctl enable mariadb –now3、 查看启动状态 [rootecs-3f21 ~]# systemctl status mariadb4、 初始化mariadb并设置root密码 [rootecs-3f21 ~]# mysql_secure_inst…...

FPGA——基础知识合集
文章目录 前言1、简述触发器与锁存器的区别2、简述 if-else 语句和 case 语句的区别3、相对 ARM、DSP 等处理器,谈谈 FPGA 具有哪些优势4、简述 Verilog 语句中阻塞赋值与非阻塞赋值的含义与区别,以及各自的适用的场景5、什么是同步电路,什么…...
【pytest】 标记冒烟用例 @pytest.mark.smoke
1. 使用 pytest.mark.smoke 标记用例 import pytest class Test_Smoke:def test_01(self):assert 112pytest.mark.smokedef test_02(self):assert 121pytest.mark.smokedef test_03(self):assert 1 2 3 2.配置文件pytest.ini [pytest] markers smoke 3. 运行指定标签 运…...
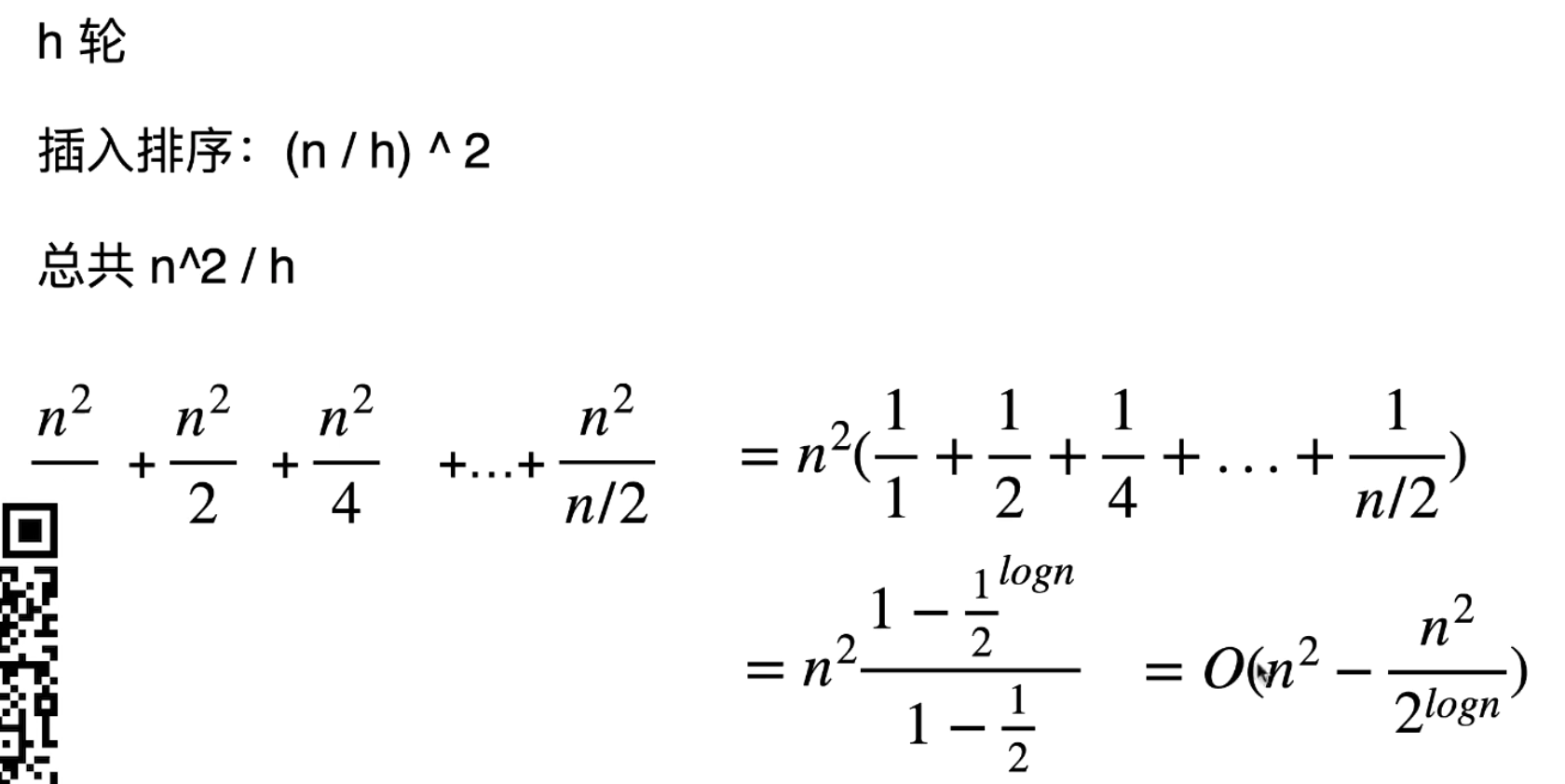
数据结构入门-14-排序
一、选择排序 1.1 选择排序思想 先把最小的元素拿出来 剩下的,再把最小的拿出来 剩下的,再把最小的拿出来 但是这样 空间复杂度是O(n) 优化一下,希望原地排序 1.1.2 选择原地排序 索引i指向0的位置 索引j指向i1的元素 j 后面的元素遍历&…...
Gin学习记录4——Controller和中间件
一. Controller 用不同的Controller可以实现业务的分类,不同类型的请求可以共用同一套中间件 1.1 单文件Controller 几乎等同于函数封装,直接将ctrl的代码写入到一个文件里然后调用: package adminimport ("net/http""git…...
FL Studio21.2中文版数字音乐制作软件
现在的FL也可以像splice一样啦,需要什么样的声音只需在fl里搜索,就会自动展示给你! FL Studio 简称FL,全称:Fruity Loops Studio,国人习惯叫它"水果"。软件现有版本是 FL Studio 21,已全面升级支…...

ELK 企业级日志分析系统 ELFK
目录 一、概述 二、组件介绍 2.1、ElasticSearch 2.2、Kiabana 2.3、Logstash 2.4、可以添加的其它组件:Filebeat 2.5、缓存/消息队列(redis、kafka、RabbitMQ等) 2.6、Fluentd 三、ELK工作原理 四、实例演示 1.ELK之 部署"E&q…...

IDEA中创建Java Web项目方法1
以下过程使用IntelliJ IDEA 2021.3 一、File-> New -> Project... 1. 项目类型中选择 Java Enterprise 项目 2. Name:填写自己的项目名称 3. Project template:选择项目的模板,Web application。支持JSP和Servlet的项目 4. Applica…...

源码:TMS FlexCel Studio for .NET 7.19
TMS FlexCel Studio for .NET 是100% 托管代码 Excel 文件操作引擎以及 Excel 和 PDF 报告生成,适用于 .NET、Xamarin.iOS、Xamarin.Android、Xamarin.Mac、Windows Phone 和 Windows Store 功能概述 使用 FlexCel Studio for .NET 创建可动态快速读写 Excel 文件的…...

多输入多输出 | MATLAB实现PSO-BP粒子群优化BP神经网络多输入多输出
多输入多输出 | MATLAB实现PSO-BP粒子群优化BP神经网络多输入多输出 目录 多输入多输出 | MATLAB实现PSO-BP粒子群优化BP神经网络多输入多输出预测效果基本介绍程序设计往期精彩参考资料 预测效果 基本介绍 Matlab实现PSO-BP粒子群优化BP神经网络多输入多输出预测 1.data为数据…...
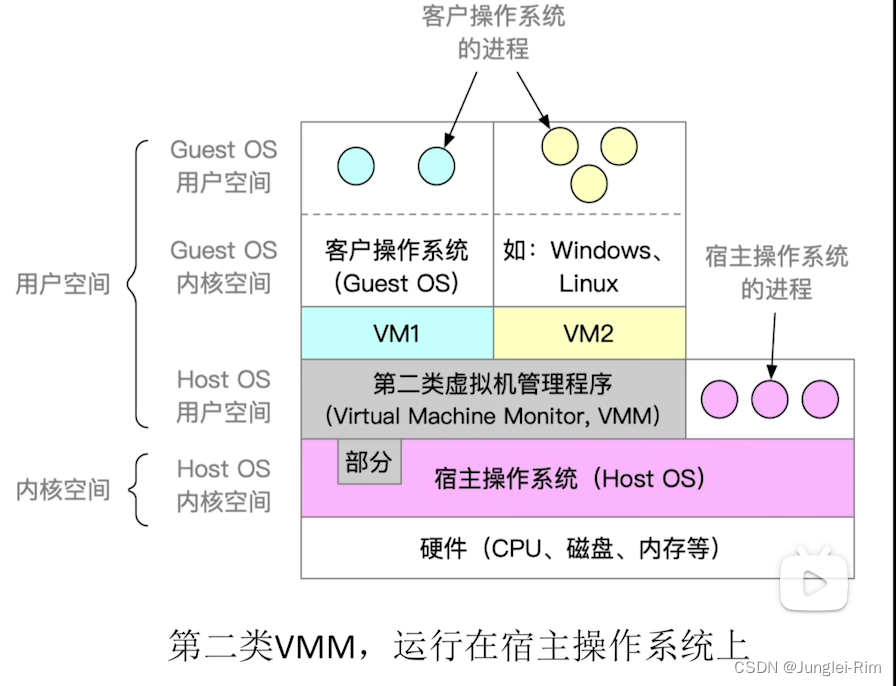
操作系统:系统引导以及虚拟机
1.操作系统引导的过程 ①CPU从一个特定主存地址开始取指令,执行ROM中的引导程序(先进行硬件自检,再开机)②将磁盘的第一块:主引导记录读入内存,执行磁盘引导程序,扫描分区表③从活动分区(又称主…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
