树形DP杂题
引
对老师布置的题目稍微记录一下吧
也算对树形 D P DP DP 的巩固
T1 Ostap and Tree
题目传送门
由于有 距离 k 距离k 距离k 的限制,设计二维 d p dp dp
设计状态:
f i , j : i 的子树内,离 i 最近的染色点与 i 距离为 j 且若 j < = k , 那么 i 的子树满足题目限制的方案数 f_{i,j}:i的子树内 ,离i最近的染色点与i距离为j\\ 且若j<=k,那么i的子树满足题目限制的方案数 fi,j:i的子树内,离i最近的染色点与i距离为j且若j<=k,那么i的子树满足题目限制的方案数
状态转移:
考虑父节点 u u u 与 子节点 v v v 的合并
若枚举 i , j i,j i,j ,那么考虑 f u , i f_{u,i} fu,i 与 f v , j f_{v,j} fv,j 可以转移到哪里
我们有 :
1.当 i + j ≤ k ∗ 2 i+j\leq k*2 i+j≤k∗2 时
\quad f u , min ( i , j ) ← f u , i ∗ f v , j f_{u,\min(i,j)} \gets f_{u,i} *f_{v,j} fu,min(i,j)←fu,i∗fv,j
2.当 i + j > k ∗ 2 i+j> k*2 i+j>k∗2 时
\quad f u , max ( i , j ) ← f u , i ∗ f v , j f_{u,\max(i,j)} \gets f_{u,i} *f_{v,j} fu,max(i,j)←fu,i∗fv,j
只能说都是状态设计的功劳
#include <algorithm>
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long long ll;
const int N=2e2+7,K=55 , INF=1e9;
const ll mod=1e9+7;
int n,k;
ll f[N][K],ans;
vector<int> G[N];
void dfs(int u,int fa) {f[u][0]=f[u][k+1]=1;for(int v:G[u]) {if(v== fa) continue; dfs(v,u);vector<ll> tmp(k*2+5) ;for(int i=0;i<=k<<1;i++) for(int j=0;j<=k<<1;j++) {if(i+j<=(k<<1))tmp[min(i,j+1)]=(tmp[min(i,j+1)]+f[u][i]*f[v][j]%mod)%mod;else tmp[max(i,j+1)]=(tmp[max(i,j+1)]+f[u][i]*f[v][j]%mod) %mod;}for(int i=0;i<=k<<1;i++) f[u][i]=tmp[i];}
}
int main() {scanf("%d%d",&n,&k);for(int i=1,u,v;i<n;i++) {scanf("%d%d",&u,&v);G[u].push_back(v),G[v].push_back(u);}dfs(1,0);for(int i=0;i<=k;i++) ans=(ans+f[1][i])%mod;printf("%lld\n",ans);
}
T2 实验比较
题目传送门
显然 ,根据 < < < 关系建边, = = = 缩点
若没有 = = = ,那么这将是一道十分友好的题,稍微运用一下组合数学即可,状态也会十分简单
多设一维限制 = = = 等号即可,注意判环的无解情况
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
inline int read() {int res = 0; bool bo = 0; char c;while (((c = getchar()) < '0' || c > '9') && c != '-');if (c == '-') bo = 1; else res = c - 48;while ((c = getchar()) >= '0' && c <= '9')res = (res << 3) + (res << 1) + (c - 48);return bo ? ~res + 1 : res;
}
inline char get() {char c; while ((c = getchar()) != '<' && c != '='); return c;
}
const int N = 135, M = 265, ZZQ = 1e9 + 7;
int n, m, X[N], Y[N], fa[N], ecnt, nxt[M], adj[N], go[M], in[N], cnt[N],
f[N][N], sze[N], C[N][N], g[N];
bool eq[N], its[N];
void init() {int i, j; for (i = 0; i <= 120; i++) C[i][0] = 1;for (i = 1; i <= 120; i++) for (j = 1; j <= i; j++)C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % ZZQ;
}
void add_edge(int u, int v) {nxt[++ecnt] = adj[u]; adj[u] = ecnt; go[ecnt] = v;nxt[++ecnt] = adj[v]; adj[v] = ecnt; go[ecnt] = u;
}
int cx(int x) {if (fa[x] != x) fa[x] = cx(fa[x]);return fa[x];
}
bool zm(int x, int y) {int ix = cx(x), iy = cx(y);if (ix != iy) fa[iy] = ix;else return 1;return 0;
}
void dfs(int u, int fu) {int i, j, k; sze[u] = f[u][1] = 1;for (int e = adj[u], v; e; e = nxt[e]) {if ((v = go[e]) == fu) continue; dfs(v, u);for (i = 1; i <= n; i++) g[i] = 0;for (i = 1; i <= sze[u] + sze[v]; i++) for (j = 1; j <= sze[u]; j++)for (k = 1; k <= sze[v]; k++) {int x = k - i + j; if (x < 0) continue;(g[i] += 1ll * f[u][j] * f[v][k] % ZZQ *C[i - 1][j - 1] % ZZQ * C[j - 1][x] % ZZQ) %= ZZQ;}for (i = 1; i <= sze[u] + sze[v]; i++) f[u][i] = g[i];sze[u] += sze[v]; }
}
int main() {int i; n = read(); m = read(); init();for (i = 1; i <= n; i++) fa[i] = i;for (i = 1; i <= m; i++) X[i] = read(),eq[i] = get() == '=', Y[i] = read();for (i = 1; i <= m; i++) if (eq[i]) zm(X[i], Y[i]);for (i = 1; i <= n; i++) its[in[i] = cx(i)] = 1;for (i = 1; i <= n; i++) fa[i] = i;for (i = 1; i <= m; i++)if (!eq[i]) {add_edge(in[X[i]], in[Y[i]]); cnt[in[Y[i]]]++;if (zm(in[X[i]], in[Y[i]])) return printf("0\n"), 0;}for (i = 1; i <= n; i++) if (its[i] && !cnt[i]) add_edge(n + 1, i);int ans = 0; dfs(n + 1, 0); for (i = 1; i <= sze[n + 1]; i++)ans = (ans + f[n + 1][i]) % ZZQ; cout << ans << endl;return 0;
}
T3 podjela
题目传送门
对题目中的限制,第二维开不下…
观察到答案的数量级应该是与 n n n 同阶
严谨的证明一下就是 a n s ≤ n − 1 ans\le n-1 ans≤n−1
因为 n − 1 n-1 n−1 次后我们一定可以将每一条边遍历到,合理规划方案即可满足条件
那么就有了状态,将答案放进状态中,最后统计合法的最值即可
设计状态:
f i , j : i 的子树中,操作 j 次后,除 i 的节点都合法, i 最多能获得的钱 f_{i,j} :i的子树中,操作j次后,除i的节点都合法,i最多能获得的钱 fi,j:i的子树中,操作j次后,除i的节点都合法,i最多能获得的钱
注意,可能会欠款,也就是 f i , j < 0 f_{i,j}<0 fi,j<0
状态转移:
转移是个树上背包
f u , i + j + 1 ← f u , i + f v , j ( v 的钱转移到 i 上 ) 若 v 不欠款,即 f v , j ≥ 0 , 就有 f u , i + j ← f u , i f_{u,i+j+1}\gets f_{u,i}+f_{v,j}(v的钱转移到i上)\\ 若v不欠款,即f_{v,j}\ge0,就有f_{u,i+j}\gets f_{u,i} fu,i+j+1←fu,i+fv,j(v的钱转移到i上)若v不欠款,即fv,j≥0,就有fu,i+j←fu,i
a n s ans ans就是第一个 f 1 , i ≥ 0 f_{1,i}\ge0 f1,i≥0时取i即可
#include <algorithm>
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
typedef long long ll;
const int N=2e3+7,INF=1e9;
int n,X;
int v[N],f[N][N],sz[N],g[N];
vector<int>G[N];
void dfs(int u,int fa) {for(int i=0;i<=n;i++) f[u][i]=-INF;f[u][0]=X-v[u],sz[u]=1;for(int v:G[u]) {if(v==fa) continue;dfs(v,u); sz[u]+=sz[v];for(int i=0;i<=sz[u]+1;i++) g[i]=-INF;for(int i=0;i<=sz[u]-sz[v];i++) {for(int j=0;j<=sz[v];j++) {g[i+j+1]=max(g[i+j+1],f[u][i]+f[v][j]);if(f[v][j]>=0) g[i+j]=max(g[i+j],f[u][i]);}}for(int i=0;i<=sz[u]+1;i++) f[u][i]=g[i];}
}
int main(){scanf("%d%d",&n,&X);for(int i=1;i<=n;i++) scanf("%d",&v[i]);for(int i=1,u,v;i<n;i++) {scanf("%d%d",&u,&v);G[u].push_back(v),G[v].push_back(u);}dfs(1,0);for(int i=0;i<n;i++) if(f[1][i]>=0) return printf("%d\n",i),0;
}
T4 赛道修建
题目传送门
- 二分答案 + 贪心 二分答案+贪心 二分答案+贪心 即可,贪心时用好 s e t set set 即可
据说可以用 v e c t o r vector vector 维护,不过又不卡 s e t set set 不用白不用
代码虚长
#include <algorithm>
#include <iostream>
#include <set>
using namespace std;
const int N=5e4+7;
int n,m,head[N],tot,ans,up;
struct node{ int to,next,w; }e[N<<1];multiset<int> s[N];
multiset<int>::iterator it;inline int read(){register int x=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}return (f==1)?x:-x;
}void Add(int x,int y,int w){e[++tot]=(node) {y,head[x],w};head[x]=tot;
}int Dfs(int x,int fa,int k){s[x].clear();for(int i=head[x],y,val;i;i=e[i].next){y=e[i].to; if(y==fa) continue;val=Dfs(y,x,k)+e[i].w;if(val>=k) ans++;else s[x].insert(val);}int Max=0;while(!s[x].empty()){if(s[x].size()==1) return max(Max,*s[x].begin());it=s[x].lower_bound(k-*s[x].begin());if(it==s[x].begin()&&s[x].count(*it)==1) it++;if(it==s[x].end()){Max=max(Max,*s[x].begin());s[x].erase(s[x].begin());}else {ans++;s[x].erase(s[x].find(*it));s[x].erase(s[x].find(*s[x].begin()));}}return Max;
}int Check(int k){ans=0;Dfs(1,0,k);return (ans>=m);
}int Dfs1(int x,int fa){int sum1=0,sum2=0;for(int i=head[x],y;i;i=e[i].next){y=e[i].to; if(y==fa) continue;sum2=max(sum2,Dfs1(y,x)+e[i].w);if(sum1<sum2) swap(sum1,sum2);//最大与次大}up=max(up,sum1+sum2);return sum1;
}int main(){n=read(),m=read();for(int i=1,x,y,w;i<n;i++){x=read(),y=read(),w=read();Add(x,y,w);Add(y,x,w);}Dfs1(1,0);int l=1,r=up,mid;while(l<r){mid=(l+r+1)>>1;if(Check(mid)) l=mid;else r=mid-1;}printf("%d\n",l);
}
T5 Aerial Tramway
题目传送门
很有意思的一题,直入主题
引用别人的话:
我们首先发觉每个可以连的区间都是不相交的,只有相邻和包含关系,所以是 O ( n ) O(n) O(n) 个(其实最多只有 n 2 \frac{n}{2} 2n 个)。然后这段区间跟相邻的是没有关系的。跟这段区间有关的只有包含的区间。所以我们可以递归的考虑这个问题。
一段区间与其包含的区间之间建边
设计状态:
f i , j , k : i 的子树分配了 j 个缆车,子树内被覆盖最多的点被覆盖了 k 次 f_{i,j,k}:i的子树分配了j个缆车,子树内被覆盖最多的点被覆盖了k次 fi,j,k:i的子树分配了j个缆车,子树内被覆盖最多的点被覆盖了k次
状态转移
是一个经典的树上背包,注意 前缀 max 前缀\max 前缀max 优化,单次求解为 O ( n 2 ) O(n^2) O(n2)
总的复杂度为 O ( T n 2 ) O(Tn^2) O(Tn2)
#include <algorithm>
#include <iostream>
using namespace std;
const int N=2e2+7,INF=1e9;
int n,m,k,ca,cb,ans;
int x[N],y[N],b[N],g[N],nxt[N],sz[N],f[N][N][10],t[N][10];
struct st {int l,r,w;} a[N];
inline void up(int&a,int b){if(a<b)a=b;}
void dfs(int x){for(int a=0;a<=m;a++) for(int b=0;b<=k;b++) f[x][a][b]=-INF;f[x][0][0]=0;for(int i=g[x];i;i=nxt[i]){dfs(i);for(int a=min(sz[x]+sz[i],m);i>=m;i--) for(int b=0;b<=k;b++) t[a][b]=f[x][a][b];for(int a=min(sz[x],m);~a;a--) for(int c=min(sz[i],m-a);~c;c--) {int t1=-INF,t2=-INF;for(int b=0;b<=k;b++) {up(t1,f[i][c][b]); up(t2,f[x][a][b]);up(t[a+c][b],max(f[x][a][b]+t1,f[i][c][b]+t2));}}sz[x]+=sz[i];for(int a=min(sz[x],m);a>=m;a--) for(int b=0;b<=k;b++) f[x][a][b]=t[a][b];}if(!x)return;sz[x]++;for(int a=min(sz[x],m-1);~a;a--) for(int b=k-1;~b;b--) up(f[x][a+1][b+1],f[x][a][b]+::a[x].w);
}
int main(){int T;while(~scanf("%d%d%d",&n,&m,&k)){k--;for(int i=1;i<=n;i++) scanf("%d%d",&x[i],&y[i]);for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if(y[i]==y[j]){bool flag=1;for(int k=i+1;k<j;k++) if(y[k]>=y[i]) {flag=0; break;}if(flag){if(i+1==j) b[++cb]=x[j]-x[i];else a[++ca]=(st){i+1,j-1,x[j]-x[i]};}}sort(b+1,b+cb+1,greater<int>());for(int i=2;i<=cb;i++) b[i]+=b[i-1];for(int i=1,j=0;i<=ca;i++){for(int k=1;k<=ca;k++)if(a[k].l<a[i].l&&a[k].r>a[i].r && (!j||a[k].w<a[j].w))j=k;nxt[i]=g[j],g[j]=i;}dfs(0);ans=-1;for(int i=m-cb;i<=m;i++) for(int j=0;j<=k;j++)up(ans,f[0][i][j]+b[m-i]);printf("Case %d: %d\n",++T,ans);for(int i=0;i<=ca;i++) g[i]=sz[i]=0;ca=cb=0;}
}
T6 Mousetrap
题目传送门
选好根,就是老鼠所在的位置 t t t 。
观察好性质,老鼠一进入某个子树就一定会无路可走。
考虑完情况,老鼠往根的情况二分答案
详细的题解 贴个链接别人的Blog
再贴个自己的代码:
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
const int N=1e6+7,INF=1e9;
int n,t,m,l,r,ans;
int sum[N],f[N],fa[N];
vector<int> G[N];
void dfs(int u,int ff) {int MAX=0,_MAX=0,cnt=G[u].size()-1; fa[u]=ff;if(u!=t) sum[u]=sum[ff]+cnt-1+(u==m);for(int v:G[u]) if(v!=ff) {dfs(v,u); if(f[v]>=MAX) _MAX=MAX,MAX=f[v];else if(f[v]>_MAX) _MAX=f[v];}f[u]=_MAX+cnt;
}
bool check(int k) {int cnt=1;for(int u=m,tu=u;u!=t;u=fa[u],cnt++) {int x=0;for(int v:G[u]) if(v!=fa[u] && v!=tu && f[v]+sum[u]>k) {if(!cnt) return 0;x++,cnt--;}k-=x,tu=u;}return k>=0;
}
int main(){scanf("%d%d%d",&n,&t,&m); r=n<<1;for(int i=1,u,v;i<n;i++) {scanf("%d%d",&u,&v);G[u].push_back(v),G[v].push_back(u);}dfs(t,0);f[t]=0;// for(int i=1;i<=n;i++) printf("%d: %d\n",i,f[i]); puts("");// for(int i=1;i<=n;i++) printf("%d: %d\n",i,sum[i]);puts("");while (l<=r) {int mid=l+r>>1;if(check(mid)) ans=mid,r=mid-1;else l=mid+1;}printf("%d\n",ans);
}
结
其实还有三道题,但我太懒了,就不写了贴一题目链接
[PA2015] Rozstaw szyn
[POI2017] Sabotaż
[CEOI2017] Chase
相关文章:

树形DP杂题
引 对老师布置的题目稍微记录一下吧 也算对树形 D P DP DP 的巩固 T1 Ostap and Tree 题目传送门 由于有 距离 k 距离k 距离k 的限制,设计二维 d p dp dp 设计状态: f i , j : i 的子树内,离 i 最近的染色点与 i 距离为 j 且若 j <…...
Webpack使用plugin插件自动在打包目录生成html文件
我们使用html-webpack-plugin插件可以自动在打包代码目录生成html文件 使用步骤: 一、安装依赖 在控制台中输入如下代码: npm i -D html-webpack-plugin 二、在webpack.config.js中配置插件 const HTMLPlugin require("html-webpack-plugin&q…...

图像处理与计算机视觉--第一章-计算机视觉简介-10问
第一章-计算机视觉简介-10问 1.CV与AI的关系是什么? CV(Computer Vision)是Al的子领域,它致力于使计算机能够理解和解释图像和数据,CV借助AI技术,比如深度学习/机器学习,实现目标识别,分析和处理任务。AI提供了CV所需要的算法…...

LeetCode 80. 删除有序数组中的重复项 II
文章目录 一、题目二、Java 题解 一、题目 给你一个有序数组 nums,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用…...

【前端面试题】浏览器面试题
文章目录 前言一、浏览器面试问题1.cookie sessionStorage localStorage 区别2.如何写一个会过期的localStorage,说说想法2.如何定时删除localstorage数据2.localStorage 能跨域吗2.memory cache 如何开启2.localstorage的限制2.浏览器输入URL发生了什么2.浏览器如何…...

PHP 生成 PDF文件
参考官网 Example 009 : Image() TCPDF laravel 可以使用 composer 安装 tecnickcom/tcpdf 进行使用 //require_once("../app/Extend/tcpdf/tcpdf.php"); $pdf new TCPDF();// 设置文档信息$pdf->SetCreator(懒人开发网);$pdf->SetAuthor(懒人开发网);$…...
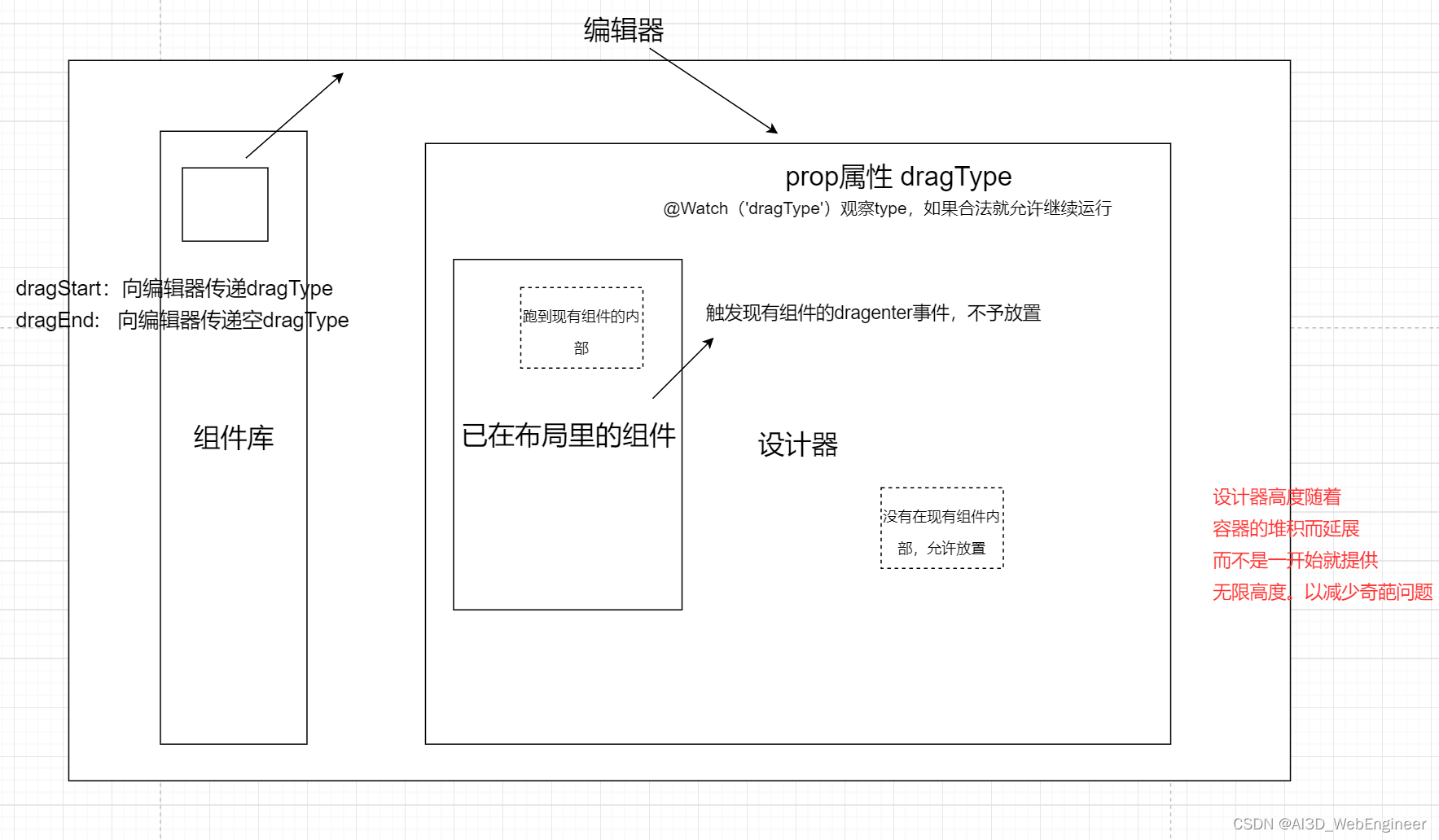
讲讲项目里的仪表盘编辑器(一)
需求 要做一个仪表盘系统,要求有: ① 设计功能(包括布局、大小、排列) ② 预览功能 ③ 运行功能 布局选择 做编辑器,肯定要先选择布局。 前端有几种常用布局。 静态布局 也叫文档布局。默认的网页形式…...

解决方案 | 如何构建市政综合管廊安全运行监测系统?
如何构建市政综合管廊安全运行监测系统?WITBEE万宾城市生命线智能监测仪器,5年免维护设计,集成10多项结构与气体健康监测指标,毫秒级快速响应,时刻感知综合管廊运行态势...

JCEF中js与java交互、js与java相互调用
jcef中js与java相互调用,java与js相互调用,chrome与java相互调用,java与chrome相互调用、jcef与java相互调用 前提:https://blog.csdn.net/weixin_44480167/article/details/133170970(java内嵌浏览器CEF-JAVA、jcef、…...

9.20 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表格 1、校招丨智行者2024年校园招聘正式启动啦 校招丨智行者2024年校园招聘正式启动啦 2、校招 | 乐动机器人2024校园招聘 校招 | 乐动机器人2024校园招聘 3、校招丨小天才2024届秋季校园招聘 …...
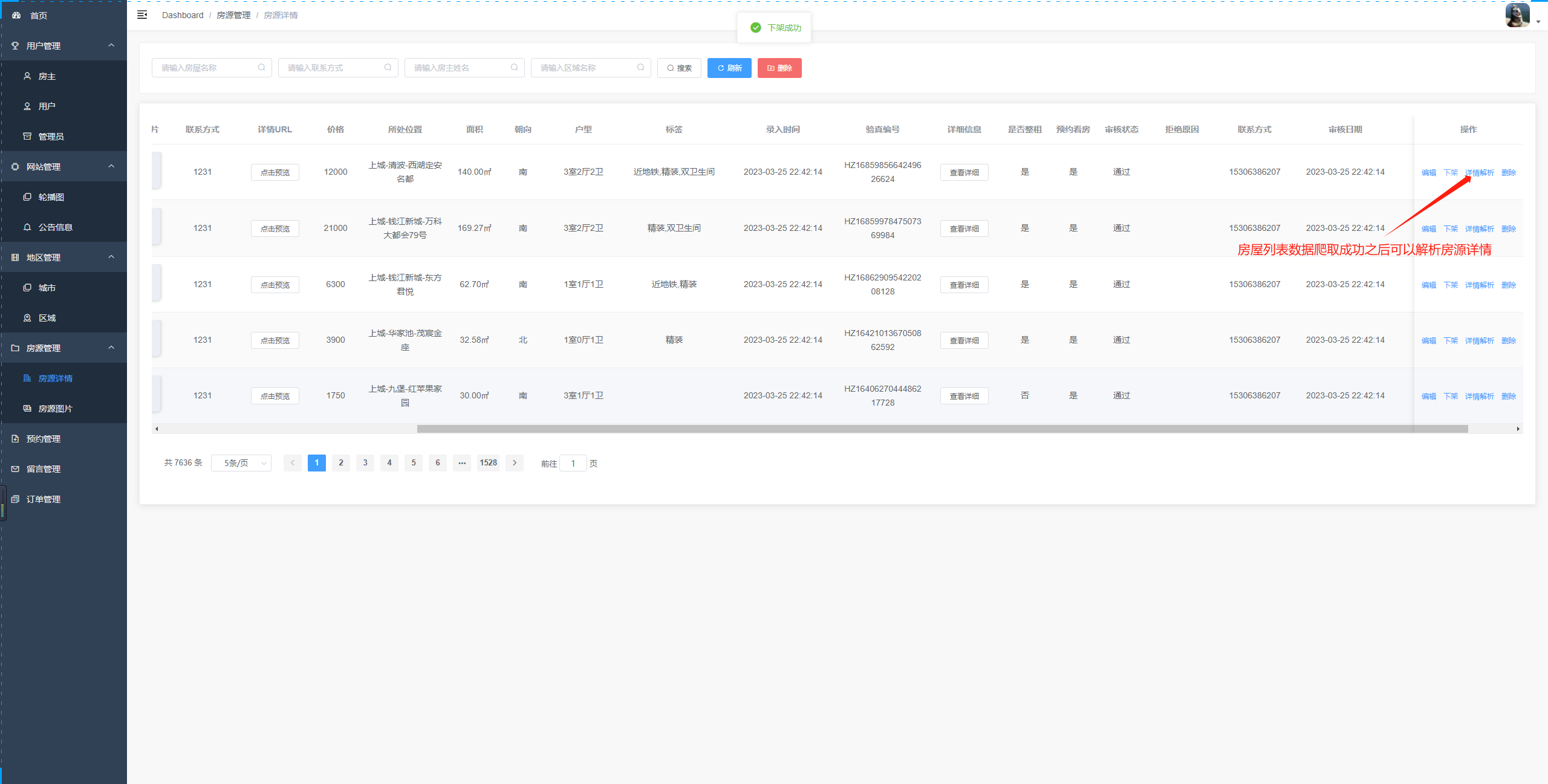
基于JAVA+SpringBoot+Vue+协同过滤算法+爬虫的前后端分离的租房系统
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 随着城市化进程的加快…...
【Android Framework系列】第16章 存储访问框架 (SAF)
1 概述 Android 4.4(API 级别 19)引入了存储访问框架 (Storage Access Framework)。SAF让用户能够在其所有首选文档存储提供程序中方便地浏览并打开文档、图像以及其他文件。 用户可以通过易用的标准 UI,以统一方式在所有应用和提供程序中浏…...
Antdesign 4中让分页组件居中显示的方法
在Ant Design 4中分页组件默认是最右边显示的,而这个没有设置位置的属性的 解决办法: 在pagination的属性中增加: style: {textAlign: "center"} 在Ant Design 5中可以让pagination使用align: center来实现分页组件居中...
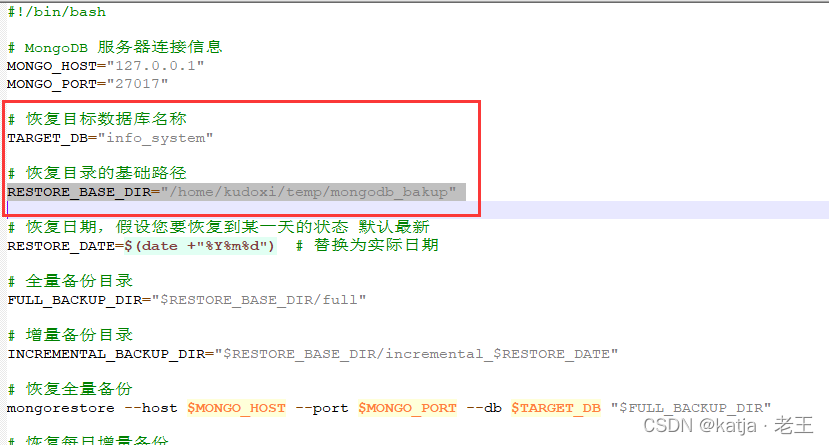
【笔记】ubuntu 20.04 + mongodb 4.4.14定时增量备份脚本
环境 ubuntu 20.04mongodb 4.4.14还没实际使用(20230922)后续到10月底如果有问题会修改 原理 只会在有新增数据时生成新的备份日期目录备份恢复时,如果恢复的数据库未删除,则会覆盖数据 准备 准备一个文件夹,用于…...

c++实现的一个定时器实例
/* * author: hjjdebug * date : 2023年 09月 23日 星期六 11:52:29 CST * description: 用std::thread 实现了一个定时器,深刻理解一下定时器是怎样工作的. * 参考Timer.h, Timer.cpp */ $ cat main.cpp #include "Timer.h" #include <unis…...
Python线程和进程
1、深度解析Python线程和进程 一篇文章带你深度解析Python线程和进程 - 知乎使用Python中的线程模块,能够同时运行程序的不同部分,并简化设计。如果你已经入门Python,并且想用线程来提升程序运行速度的话,希望这篇教程会对你有所帮…...
)
算法 寻找峰值-(二分查找+反向双指针)
牛客网: BM19 题目: 寻找数组峰值,可能多个返回任一个,每个值满足nums[i] ! nums[i 1] 思路: 双指针 left 0, right n-1, 相向而行,取中间位置mid, nums[mid]与nums[mid1]比较,如果nums[mid] < nums[mid1],说明…...

【数据结构】—交换排序之快速排序究极详解,手把手带你从简单的冒泡排序升级到排序的难点{快速排序}(含C语言实现)
食用指南:本文在有C基础的情况下食用更佳 🔥这就不得不推荐此专栏了:C语言 ♈️今日夜电波:靴の花火—ヨルシカ 0:28━━━━━━️💟──────── 5:03 …...
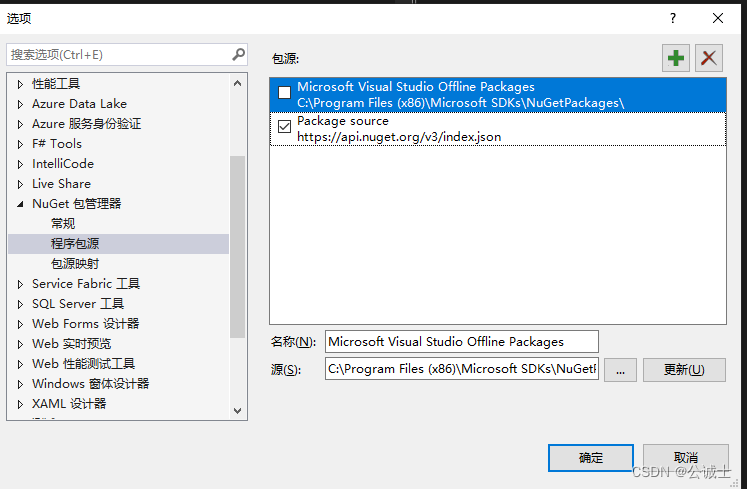
【c#-Nuget 包“在此源中不可用”】 Nuget package “Not available in this source“
标题c#-Nuget 包“在此源中不可用”…但 VS 仍然知道它吗? (c# - Nuget package “Not available in this source”… but VS still knows about it?) 背景: 今日从公司svn 上拉取很久很久以前的代码,拉取下来200报错,进一步发…...
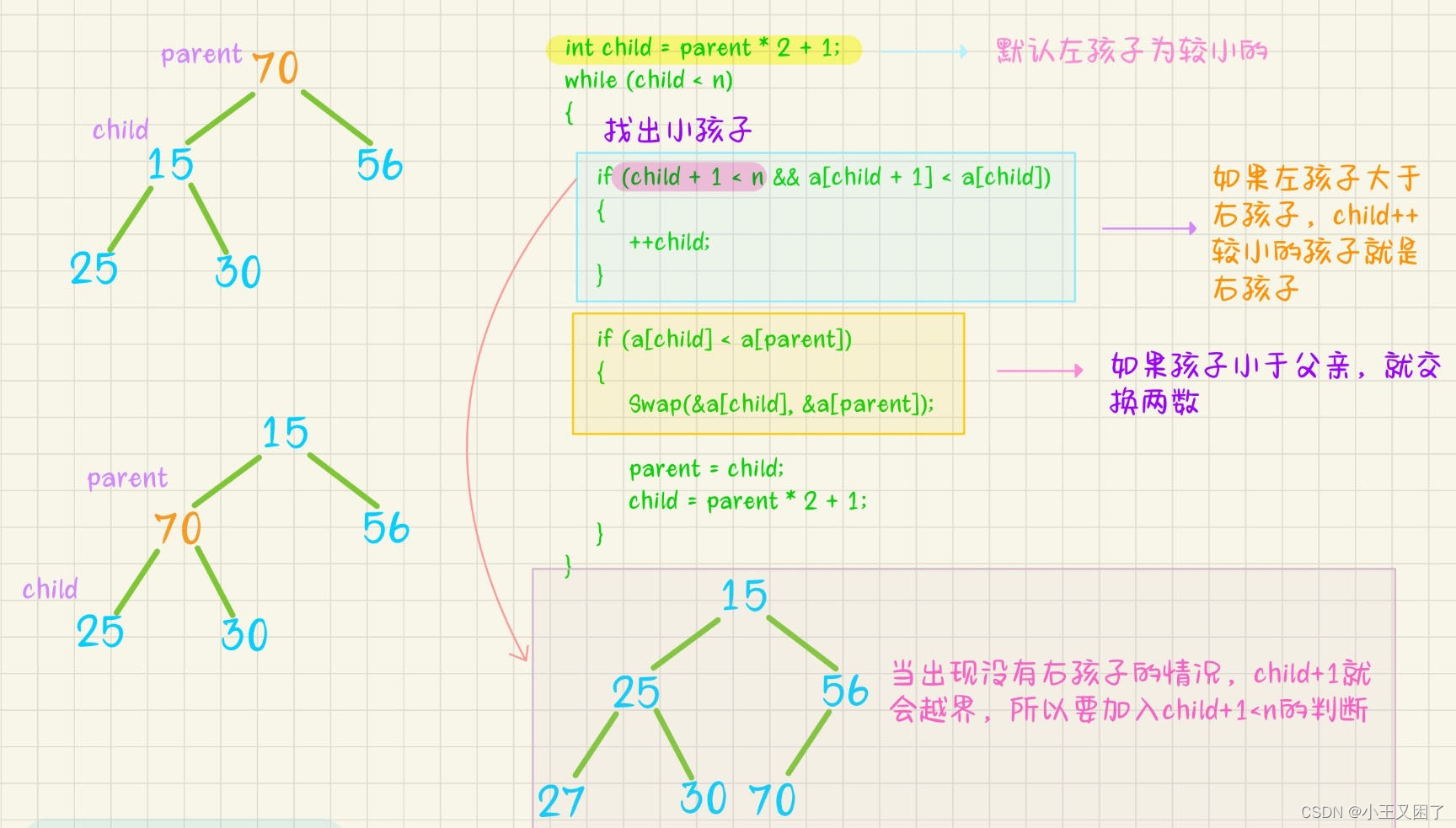
【数据结构】二叉树之堆的实现
🔥博客主页:小王又困了 📚系列专栏:数据结构 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、二叉树的顺序结构 📒1.1顺序存储 📒1.2堆的性质…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
