【完全二叉树魔法:顺序结构实现堆的奇象】
本章重点
- 二叉树的顺序结构
- 堆的概念及结构
- 堆的实现
- 堆的调整算法
- 堆的创建
- 堆排序
- TOP-K问题

1.二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
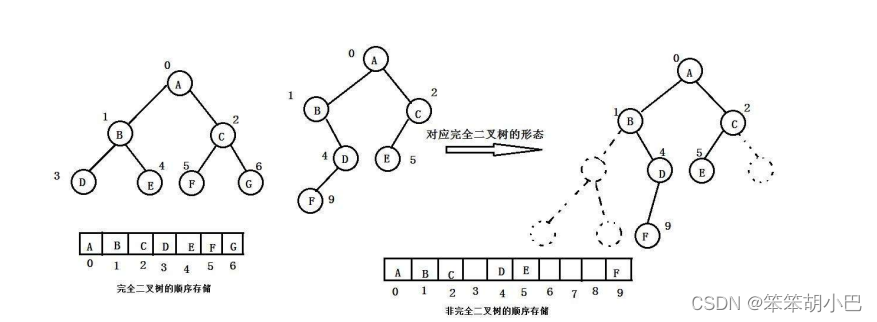
访问结点的规律:
//访问孩子节点
leftchild = parent*2+1
rightchild = parent*2+2//访问父亲结点
parent = (child-1)/22.堆的概念及结构

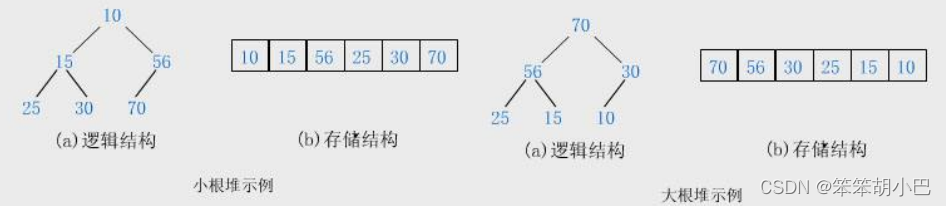
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
- 大堆:任何父亲节点 >= 孩子结点
- 小堆:任何父亲节点 <= 孩子结点
1.下列关键字序列为堆的是:()。
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
解析:
堆(Heap)是一种特殊的树形数据结构,它通常有两种类型:小堆(Min Heap)和大堆(Max Heap)。在小堆中,父节点的值小于或等于其子节点的值,而在大堆中,父节点的值大于或等于其子节点的值。
要判断一个序列是否是堆,需要检查该序列是否满足堆的性质。我们发现A符合大堆的性质父节点的值大于或等于其子节点的值。
2.已知小根堆为8,15,10,21,34,16,12,删除关键字 8 之后需重建小堆,在此过程中,关键字之间的比较次数是()。
A 1
B 2
C 3
D 4
解析:
在一个小根堆中删除根节点后,需要重新构建小根堆。删除根节点后,通常会将堆的最后一个元素移动到根的位置,然后通过与其子节点的比较来逐级下移,以确保小根堆的性质得以恢复。
给定的小根堆是:8, 15, 10, 21, 34, 16, 12。
首先删除根节点8后,将最后一个元素12移到根的位置,得到:12, 15, 10, 21, 34, 16。
然后,我们需要逐级下移12,直到小根堆性质得以恢复。在这个过程中,我们将12与其子节点进行比较,选择较小的子节点来交换位置。
第一次比较:12与15比较,不需要交换。
第二次比较:12与10比较,需要交换。
第三次比较:12与16比较,不需要交换。
因此,关键字之间的比较次数是3次。
3.一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为()。
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2)
F(17 7 11 3 2 5)
堆排序是一种基于堆数据结构的排序算法,通常会建立一个最大堆(Max Heap)或最小堆(Min Heap)来进行排序。在这里,我们需要建立一个最大堆。
初始堆的建立过程通常是从数组的末尾开始,逐步将元素向上移动,以满足堆的性质。对于给定的排序码数组(5 11 7 2 3 17),初始堆的建立步骤如下:
4.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后,其结果是()。
A[3,2,5,7,4,6,8]
B[2,3,5,7,4,6,8]
C[2,3,4,5,7,8,6]
D[2,3,4,5,6,7,8]
3.堆的实现

这里的堆是使用数组实现的,博主重点介绍堆的删除和插入接口,其他接口同顺序表相同,这里就不过多赘述了。
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;// 堆的初始化
void HeapInit(HP* php);
// 堆的打印
void HeapPrint(HP* php);
// 堆的销毁
void HeapDestroy(HP* php);
//堆的创建
void HeapInitArray(HP*php, int* a, int n);
// 堆的插入
void HeapPush(HP* php, HPDataType x);
// 堆的删除
void HeapPop(HP* php);
// 取堆顶的数据
HPDataType HeapTop(HP* php);
// 堆的数据个数
int HeapSize(HP* php);
// 堆的判空
bool HeapEmpty(HP* php);3.1堆的插入:void HeapPush(HP* php, HPDataType x)
- 先将元素插入到堆的末尾,即最后一个孩子之后。
- 插入之后如果堆的性质遭到破坏,将信新插入节点顺着其双亲往上调整到合适位置即可,即向上调整。
- 向上调整结束的条件是child等于0,parent等于-1,但是我们写的循环结束条件是child大于0,因为parent的值不会是-1,而是0,这里可以去看我的另外一篇文章,里面介绍了c语言取整规则:链接
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType temp = *p1;*p1 = *p2;*p2 = temp;
}//向上调整
void AdjustUP(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//交换child = parent;parent = (parent - 1) / 2;}else{break;}}
}// 堆的插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if(php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* temp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newCapacity);if (temp == NULL){perror("realloc fail");exit(-1);}php->a = temp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUP(php->a, php->size - 1);
}
3.2堆的删除:void HeapPop(HP* php)
- 将堆顶元素与堆中最后一个元素进行交换。
- 删除堆中最后一个元素。
- 将堆顶元素向下调整到满足堆特性为止。
- 向下调整的结束条件是child等于叶子结点。
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType temp = *p1;*p1 = *p2;*p2 = temp;
}//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//parent到叶子结点就结束while (child < n){//可能不存在右孩子if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
// 堆的删除
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0);
}
4.堆的调整算法
4.1堆向下调整算法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
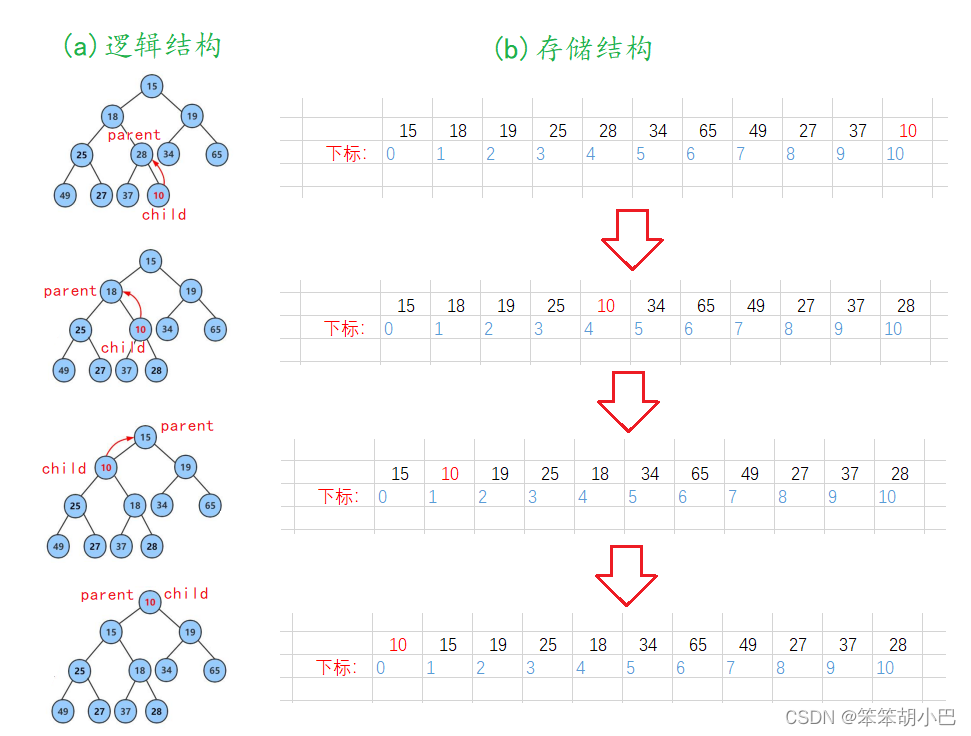
int array[] = {27,15,19,18,28,34,65,49,25,37};
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//parent到叶子结点就结束while (child < n){//可能不存在右孩子if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}4.2堆向上调整算法
现在我们给出一个数组,前n-1个数已经是堆了,现在再添加一个数要让其满足堆的性质。我们通过从最后一个叶子结点向上调整算法可以把它调整成一个小堆。向上调整算法有一个前提:前面的数据必须是一个堆,才能调整。
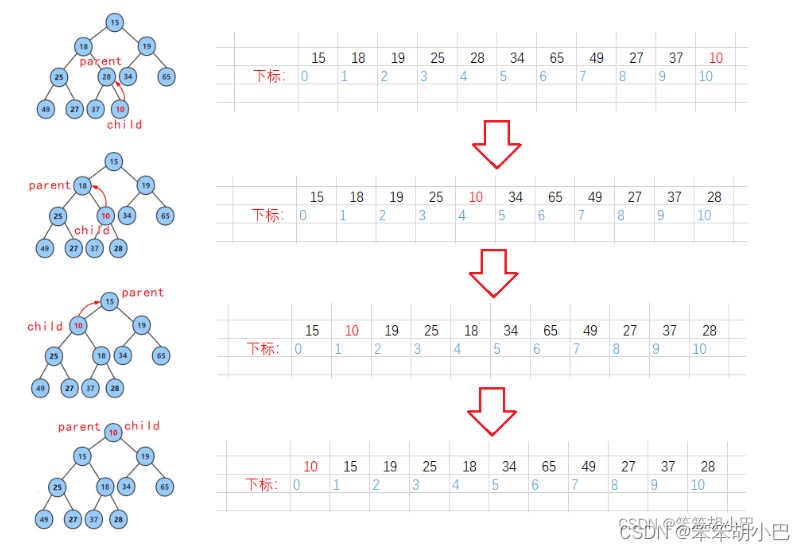
//向上调整
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}5.堆的创建
方法一:向上调整插入的思想
下面我们给出一个数组,利用上面push函数的思路,将数组a中的元素依次插入向上调整,把第一个数当成堆,满足堆向上调整的前提,可以调整成堆。
int a[] = {1,5,3,2,8};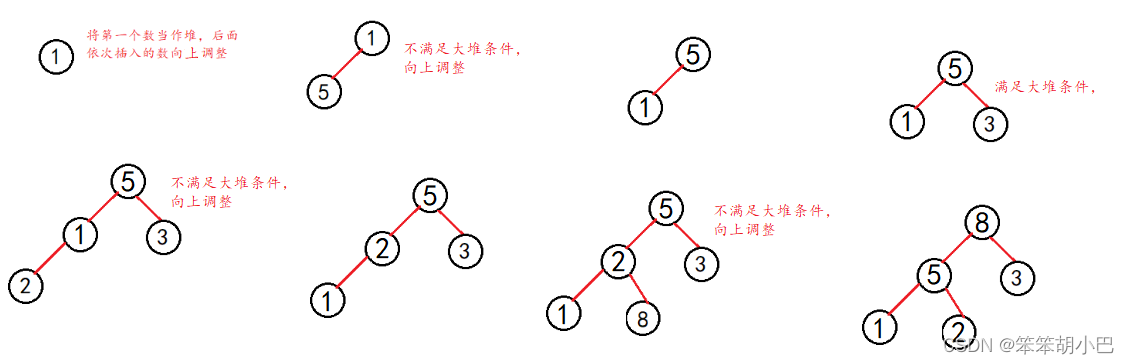
//建堆
//向上调整:前提是前面的数据是堆
// 思路:第一个数据当作堆,后面数据依次插入,向上调整
//时间复杂度O(N*logN)
for (int i = 1; i < n; i++)
{AdjustUp(a, i);
}所以这里我们就可以给堆结合实现一个创建堆的接口:使用向上调整的思路。
void HeapInitArray(HP* php, int* a, int n)
{assert(php);assert(a);php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (php->a == NULL){perror("malloc fail");exit(-1);}php->size = php->capacity = n;memcpy(php->a, a, sizeof(HPDataType) * n);for (int i = 0; i < n; i++){AdjustUp(php->a, i);}
}因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):

因此:建堆的时间复杂度为O(N*logN)。
方法二:倒数第一个非叶子结点向下调整的思想
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。如果根节点左右子树是堆,我们可以直接向下调整即可,但是此时根节点左右子树不是堆,我们怎么调整呢?这里我们从倒数的第一个非叶子节点的子树与其叶子结点开始向下调整,调整完直接下标减一就是倒数的第二个非叶子节点,一直调整到根节点的树,就可以调整成堆。
int a[] = {1,5,3,8,7,6}; //倒数第一个非叶子结点:(最后一个叶子结点-1)/2 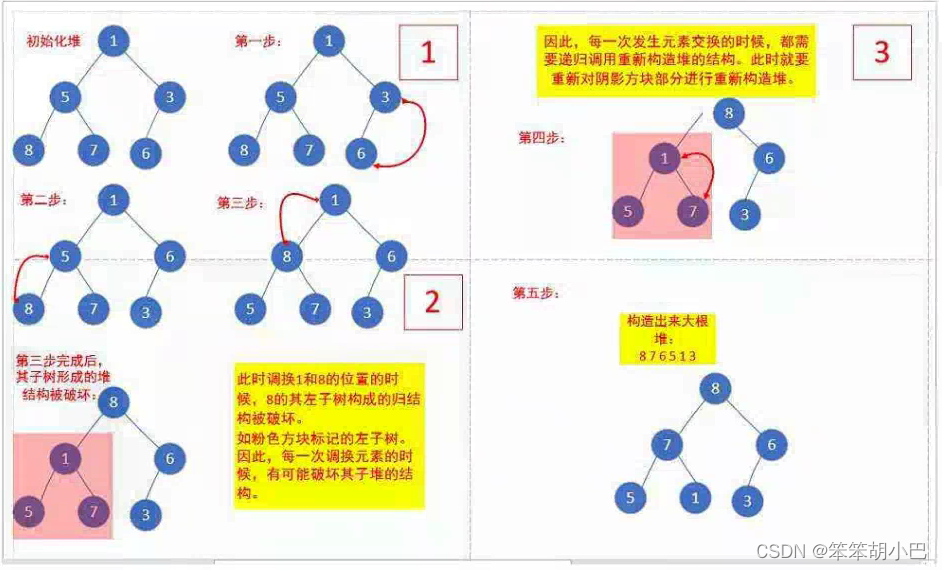
//建堆
//向下调整建堆
//找到倒数第一个非叶子结点
//时间复杂度O(N)
for (int i = (n - 1 - 1)/2; i >= 0; i--)
{AdjustDown(a, n, i);
}
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):
因此:建堆的时间复杂度为O(N)。
6.堆排序

1. 排序如何建堆
- 升序:建大堆
- 降序:建小堆
为什么升序是建大堆呢?按照我们的常理,我们先建小堆,然后再取出堆顶的数据,这样就取得了最小的数据,这样数据不就有序了,为什么要去建大堆呢???
取出堆顶的数据,这样就取得了最小的数据,然后再选次小的数,此时我们只能将剩下的数看做堆,但是剩下的数据还是堆嘛?

此时就要重新建堆,然后再取堆顶数据,再建堆...每次建堆的时间复杂度N*logN,一共有N个数据,所以总的排序时间复杂度就是N * logN * N,那还不如直接遍历一遍排序来的快呢!!!
2. 利用堆删除思想来进行排序
所以此时我们可以建大堆,将堆顶的数据和最后一个叶子结点交换,由于此时的堆结构没有破坏,左子树和右子树仍然是堆,使用堆的向下调整去调整堆,然后在缩小下次向下调整的范围,也就是把最大的那个数不算做堆的范围了,这样最大的数据就保存在了下标最大的位置处,满足了升序的要求。每次向下调整的时间复杂度是logN,一共有N个数据,所以总的排序时间复杂度就是N * logN。
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>void Swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}
//向上调整
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;//parent到叶子结点就结束while (child < n){//可能不存在右孩子if (child + 1 < n && a[child] < a[child + 1]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}}
void HeapSort1(int a[],int n)
{//建堆//向上调整:前提是前面的数据是堆// 思路:第一个数据当作堆,后面数据依次插入,向上调整//O(N*logN)for (int i = 1; i < n; i++){AdjustUp(a, i);}//升序建大堆//O(N*logN)//向下调整:前提是左右子树是堆int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
void HeapSort2(int a[],int n)
{//建堆//向下调整:前提是左右子树是堆// 思路:找到倒数第一个非叶子结点,与最后一个叶子结点进行向下调整,直至根节点//O(N)for (int i = (n - 1 - 1)/2; i >= 0; i--){AdjustDown(a, n, i);}//升序建大堆//O(N*logN)//向下调整:前提是左右子树是堆int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
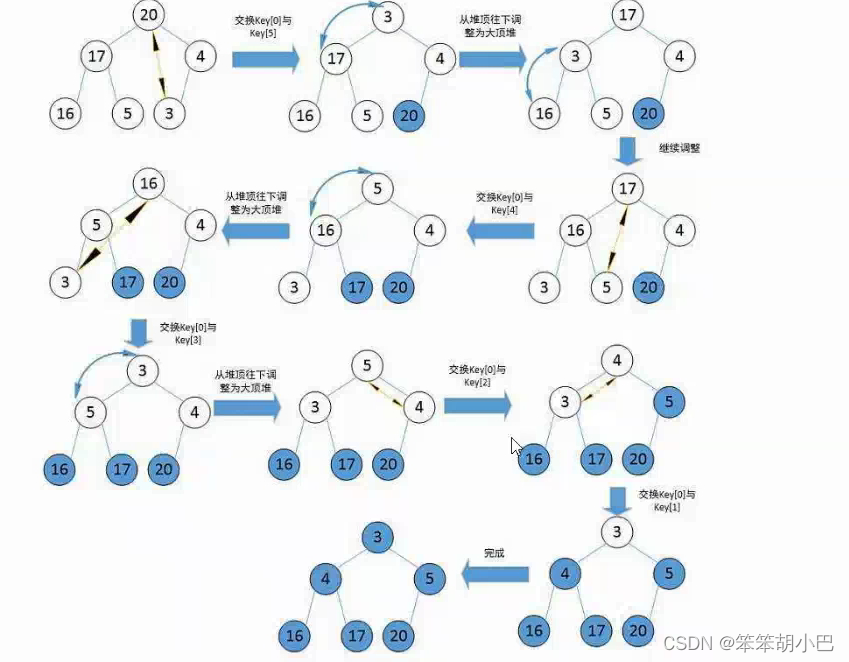
int main()
{int a[] = { 3,17,4,20,16,5 };//HeapSort1(a,sizeof(a)/sizeof(a[0]));HeapSort2(a,sizeof(a)/sizeof(a[0]));int i = 0;for (i = 0; i < sizeof(a) / sizeof(a[0]); i++){printf("%d ", a[i]);}return 0;
}运行结果:

7.TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。

比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
这里不能用大堆,如果第一个数据就是最大的,放在堆顶,其余数据就无法入堆,所以要用小堆,最大的前k个数肯定比堆顶大,此时该数替换堆顶的数入堆,入完k个后就找到前k个最大的元素。
- 前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
- 将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
3.复杂度
- 时间复杂度:O(N*logK)
- 空间复杂度:O(K)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
void Swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;//parent到叶子结点就结束while (child < n){//可能不存在右孩子if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void PrintTopK(const char *filename, int k)
{// 1. 建堆--用a中前k个元素建堆FILE* fout = fopen(filename, "r");if (fout == NULL){perror("fopen fail");exit(-1);}int *Minheap = (int*)malloc(sizeof(int) * k);if (Minheap == NULL){perror("malloc fail");exit(-1);}//读文件for (int i = 0; i < k; i++){fscanf(fout, "%d", &Minheap[i]);}//向下调整建小堆for (int i = (k-2)/2; i >= 0; --i){AdjustDown(Minheap, k, i);}// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > Minheap[0]){Minheap[0] = x;AdjustDown(Minheap, k, 0);}}for (int i = 0; i < k; ++i){printf("%d ", Minheap[i]);}printf("\n");fclose(fout);
}
void CreatNData()
{//造数据int n = 10000;srand((unsigned int)time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen fail");exit(-1);}for (int i = 0; i < n; ++i){int x = rand() % 1000000;fprintf(fin, "%d\n", x);}fclose(fin);
}
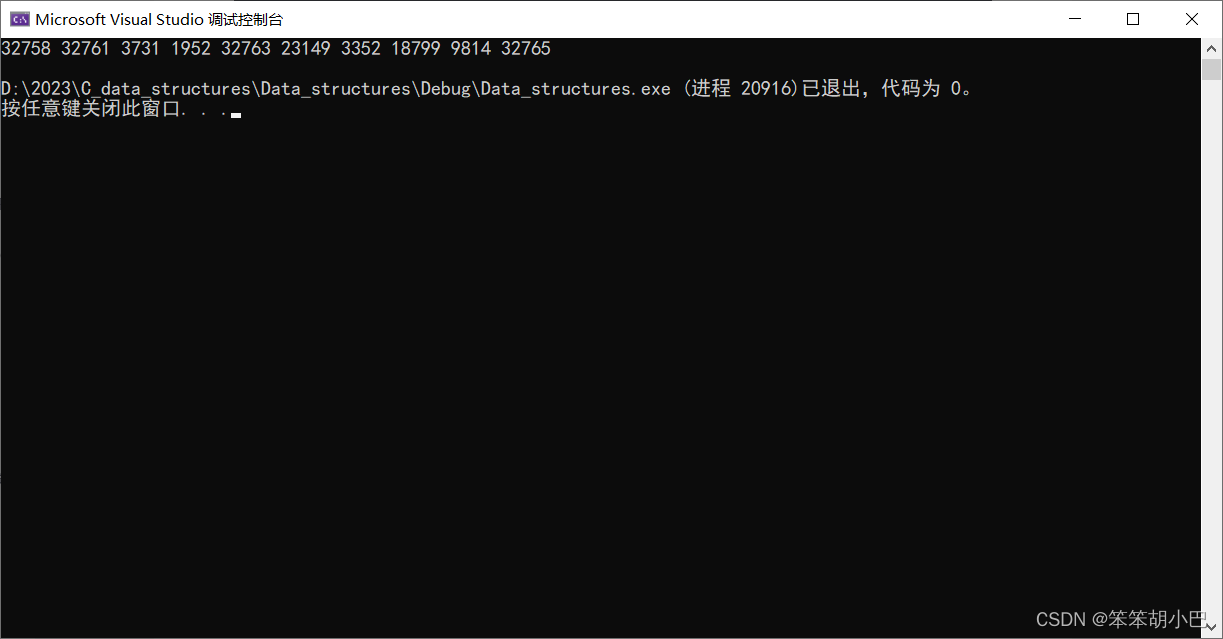
int main()
{//CreatNData();PrintTopK("data.txt",10);return 0;
}运行结果:
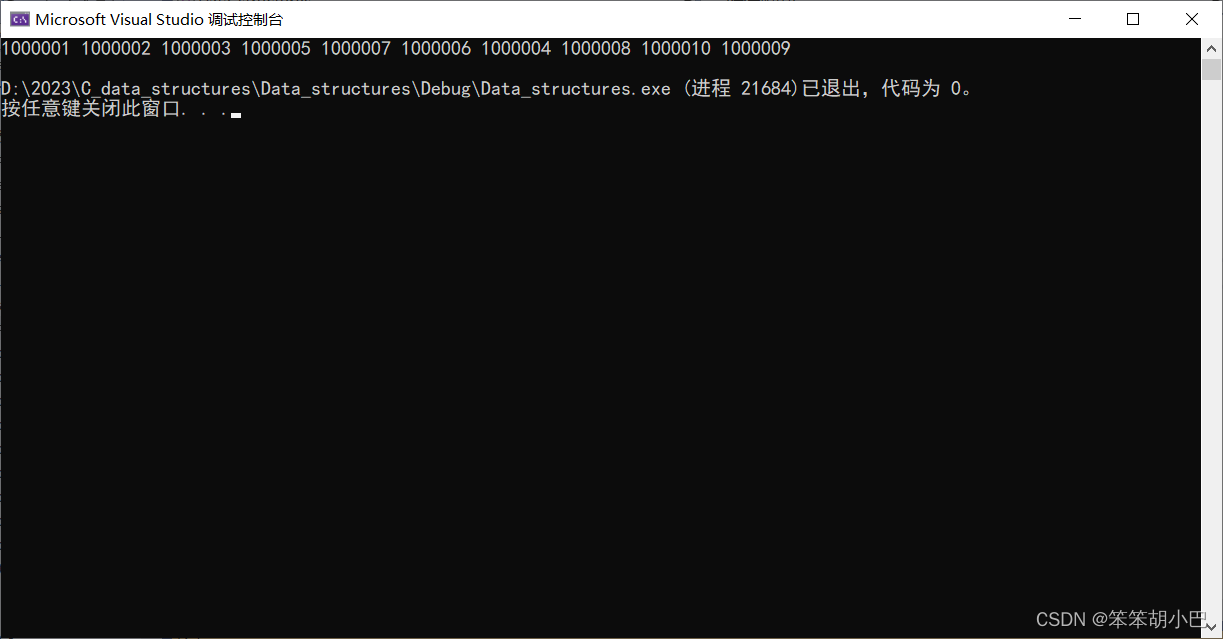
但是我们怎么知道这几个数据就是前k个最大的呢?我们可以在文件中手动创造10个最大的值,看看输出是不是我们刚刚手动创造10个最大的值。
1000001;1000002;1000003;10000041000005;
1000006;1000007;1000008;1000009;1000009。
这样就完成了我们的TOP-K问题!!!

相关文章:

【完全二叉树魔法:顺序结构实现堆的奇象】
本章重点 二叉树的顺序结构堆的概念及结构堆的实现堆的调整算法堆的创建堆排序TOP-K问题 1.二叉树的顺序结构 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构…...

Maven官方镜像仓库与阿里云云效Maven
一、Maven官方镜像仓库 download maven-3 右击复制链接地址,使用wget命令直接在linux中下载: wget 链接地址history 二、阿里云云效Maven 详情查看maven 配置指南 打开 maven 的配置文件( windows 机器一般在 maven 安装目录的 conf/…...

python系列教程215——列表解析与矩阵
朋友们,如需转载请标明出处:https://blog.csdn.net/jiangjunshow 声明:在人工智能技术教学期间,不少学生向我提一些python相关的问题,所以为了让同学们掌握更多扩展知识更好地理解AI技术,我让助理负责分享…...
fonts什么文件夹可以删除吗?fonts文件夹删除了怎么恢复
在电脑上,fonts文件夹是存放字体文件的目录之一。尽管有时可能考虑删除该文件夹以节省硬盘空间或出于其他原因,但删除该文件夹可能会导致系统字体问题,影响用户的正常使用。因此,在删除之前需要考虑是否可以删除fonts文件夹&#…...
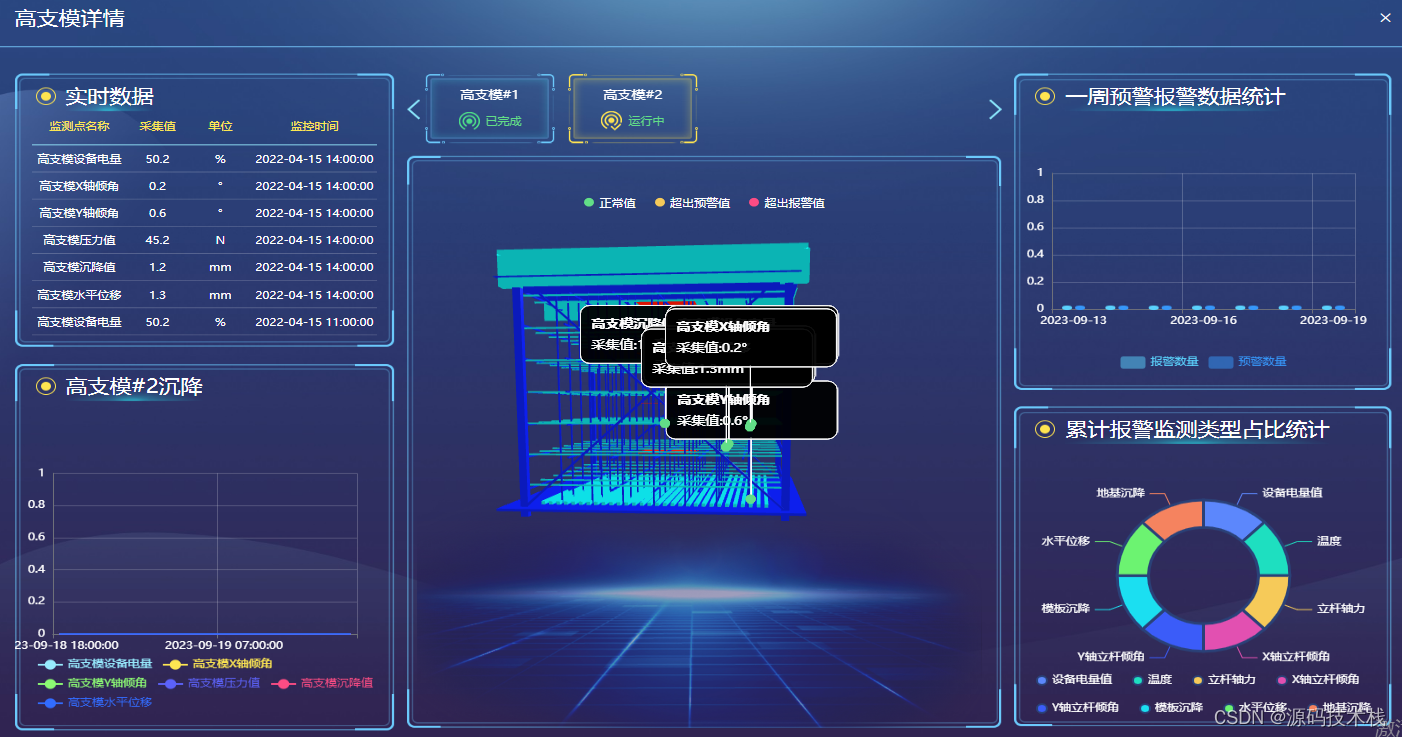
【智慧工地源码】智慧工地助力数字建造、智慧建造、安全建造、绿色建造
智慧工地围绕建设过程管理,建设项目与智能生产、科学管理建设项目信息生态系统集成在一起,该数据在虚拟现实环境中,将物联网收集的工程信息用于数据挖掘和分析,提供过程趋势预测和专家计划,实现工程建设的智能化管理&a…...

CListCtrl设置只显示单列
CListCtrl设置只显示单列 2023/9/5 下午4:07:15 要将CListCtrl控件设置为只显示单列,您可以使用SetExtendedStyle函数来设置控件的样式。下面是设置只显示单列的示例代码: cpp m_listCtrl.SetExtendedStyle(LVS_EX_GRIDLINES | LVS_EX_FULLROWSELECT | LVS_EX_HEADERDRAG…...

冒泡排序与选择排序(最low的两兄弟)
个人主页:Lei宝啊 愿所有美好如期而遇 前言: 在我们的生活中,无处不在用到排序,比如说成绩的排名,淘宝,京东等等商品在各个方面的排序,这样看来一个好的算 法很重要,接下来我们要先…...

MySQL-三大日志
前言 redo log:为了持久化数据,当内存中的数据还没写入到磁盘而宕机时,会读取该日志持久化数据到磁盘 undo log:为了保证原子性,事务的操作都会记录一条相反的sql到该日志,出现错误就会根据该文件恢…...
MySQL数据库详解 二:数据库的高级语言和操作
文章目录 1. 克隆表 ---- 将数据表的数据记录生成到新的表中1.1 方式一:先创建新表,再导入数据1.2方式二:创建的时候同时导入 2. 清空表 ---- 删除表内的所有数据2.1 delete删除2.2 truncate删除(重新记录)2.3 创建临时…...
基于springboot+vue的在线购房(房屋租赁)系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

scikit-learn机器学习算法封装
K近邻算法 K-最近邻(KNN)是一种有监督的机器学习算法,可用于解决分类和回归问题。它基于一个非常简单的想法,数据点的值由它周围的数据点决定。考虑的数据点数量由k值确定。因此,k值是算法的核心。 我们现在已经知道。…...

信息化发展56
数据开发利用 通过数据集成、数据挖掘和数据服务(目录服务、查询服务、浏览和下载服务、数据分发服务)、数据可视化、信息检索等技术手段, 帮助数据用户从数据资源中找到所需要的数据, 并将数据以一定的方式展现出来,…...
外贸进销存ERP系统源码 多店ERP系统源码
外贸进销存ERP系统源码 多店ERP系统源码 ERP系统的主要优势在于它可以将企业的所有业务流程整合到一个中央化的系统中,并通过数据共享和集成来提高企业的效率。这样,各部门之间就可以相互协作,共同完成业务流程,而不会受到信息隔…...

旅游行业怎么做微信营销?
让我们分析一下现在的旅游业市场,一方面用户的旅游需求越来越旺盛,而另一方面旅游从业者却都在抱怨市场越来越难搞,线下旅行社说:好惨,游客都跑线上大门户去订购了,我们只能吃剩下的,线上旅行社…...

Linux下du指令详情介绍
磁盘空间使用统计,方便排行哪些文件占用内存大 1.统计指定目录磁盘空间使用情况 du 目录路径2.可读形式 du -h 目录路径3.显示所有文件和目录的磁盘使用情况 du -a [目录路径]4.仅统计目录的磁盘空间使用情况,不包括子目录: du -S [目录路…...
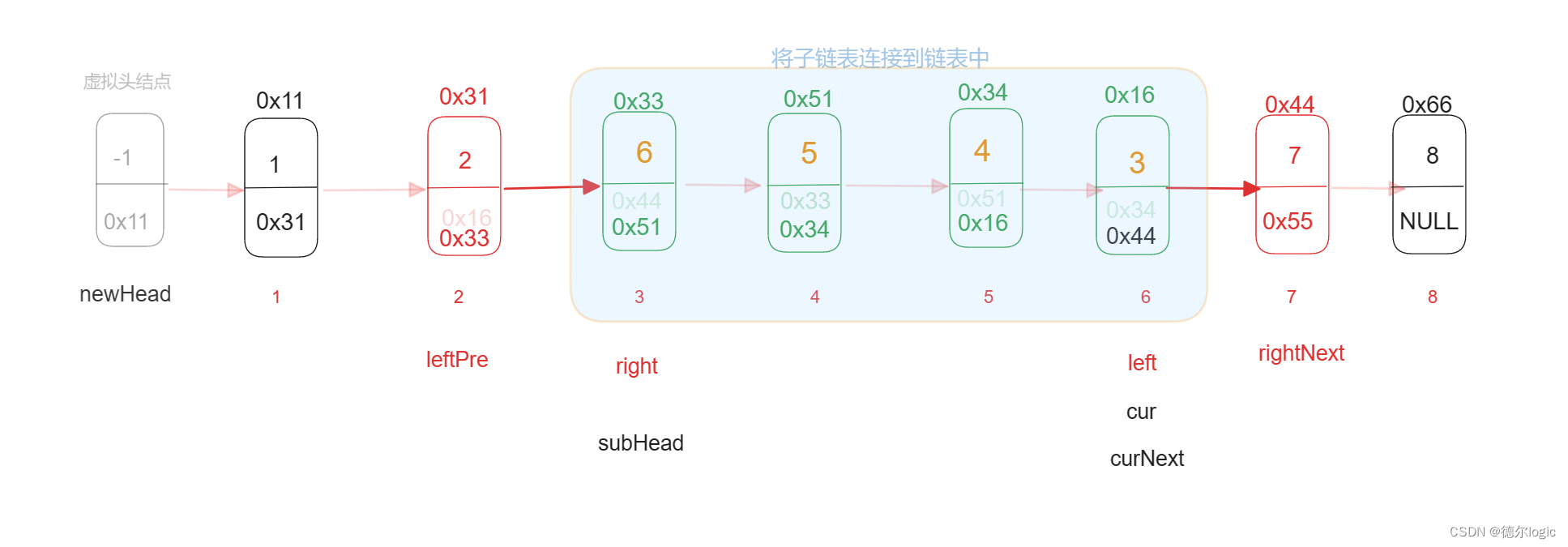
【刷题-牛客】链表内指定区间反转
链表定区间翻转链表 题目链接题目描述核心思想详细图解代码实现复杂度分析 题目链接 链表内指定区间反转_牛客题霸_牛客网 (nowcoder.com) 题目描述 核心思想 遍历链表的过程中在进行原地翻转 [m,n]翻转区间记作子链表,找到子链表的 起始节点 left 和 终止节点 right记录在…...
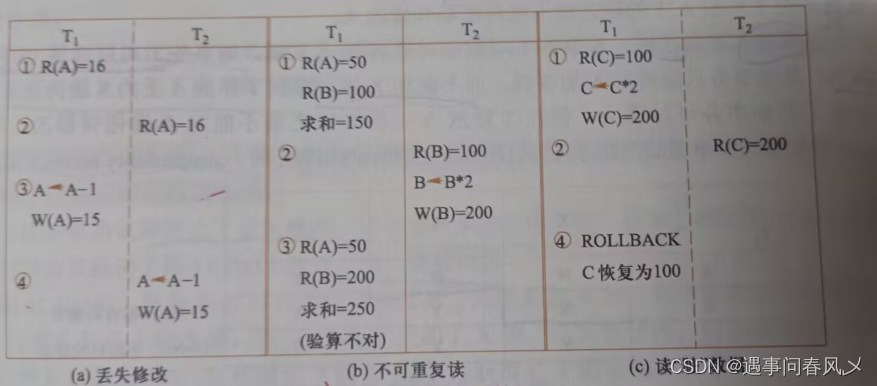
【MySQL】 MySQL索引事务
文章目录 🛫索引🎍索引的概念🌳索引的作用🎄索引的使用场景🍀索引的使用📌查看索引📌创建索引🌲删除索引 🌴索引保存的数据结构🎈B树🎈B树&#x…...
mybatis-plus异常:dynamic-datasource can not find primary datasource
现象 使用mybatis-plus多数据源配置时出现异常 com.baomidou.dynamic.datasource.exception.CannotFindDataSourceException: dynamic-datasource can not find primary datasource分析 异常原因是没有设置默认数据源,在类上没有使用DS指定数据源时,默…...
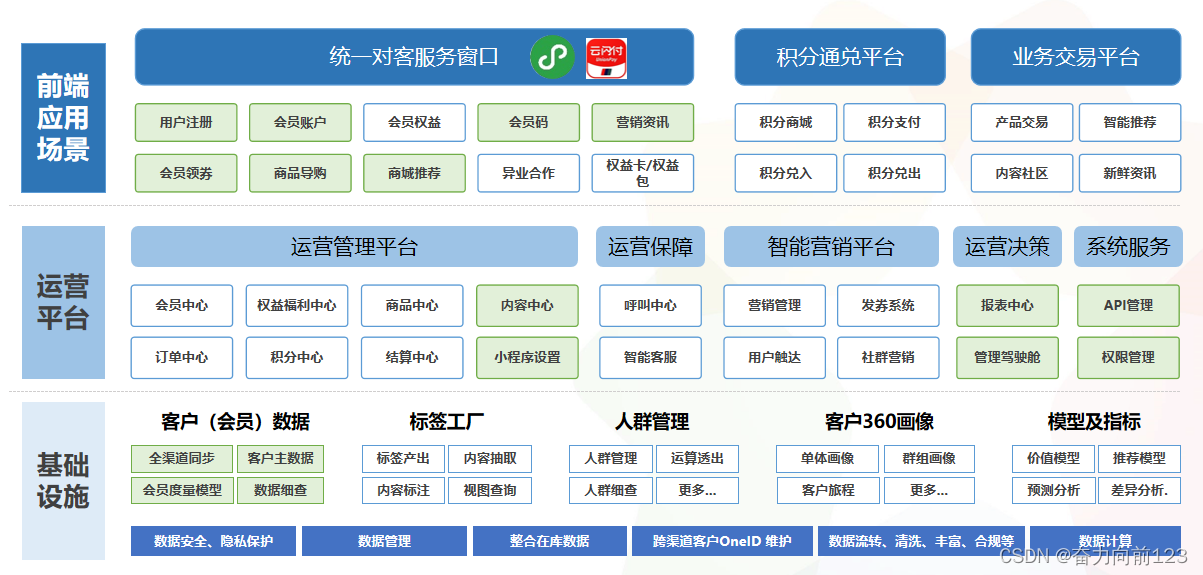
购物H5商城架构运维之路
一、引言 公司属于旅游行业,需要将旅游,酒店,购物,聚合到线上商城。通过对会员数据进行聚合,形成大会员系统,从而提供统一的对客窗口。 二、业务场景 围绕更加有效地获取用户,提升用户的LTV&a…...
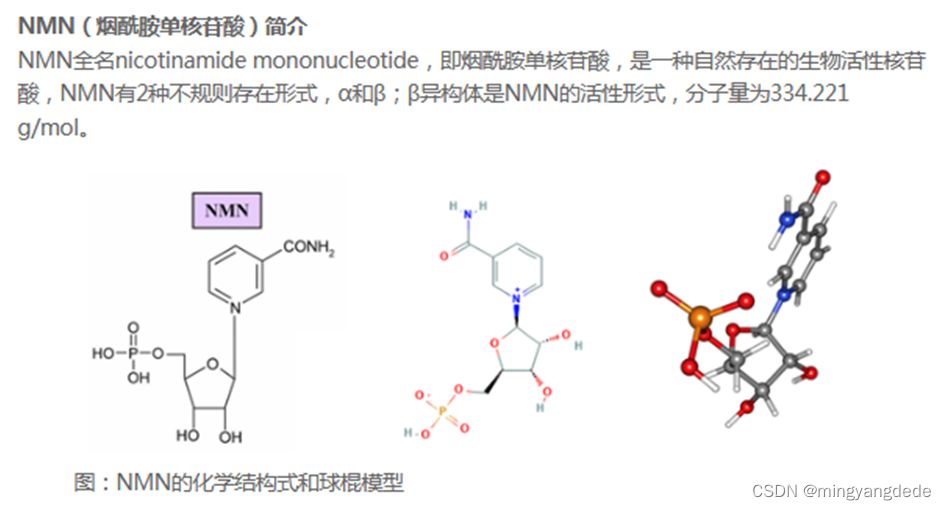
【NAD NADPH; FMN FAD ; NMN -化学】
NAD Nicotinamide adenine dinucleotide nicotinamide 烟酰胺 NAD NADPH 烟酰胺腺嘌呤二核苷酸 nucleosidase Nicotinamide adenine dinucleotide NMN(烟酰胺单核苷酸)简介 NMN全名 nicotinamide mononucleotide,即 烟酰胺单…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...