组合计数训练题解
CF40E
题目链接
点击打开链接
题目解法
首先,如果 n , m n,m n,m 一奇一偶,那么答案为 0 0 0
原因是从行和列的角度分析, − 1 -1 −1 个数的奇偶性不同
可以发现 k < max { n , m } k<\max\{n,m\} k<max{n,m} 的性质很微妙,把它转化为有用的信息,即为:
令 n > m n>m n>m,则必有一行为空
可以发现,除了空行,其他所有行只需在满足行乘积为 − 1 -1 −1 的情况下随便填,然后令空行满足列的限制即可
我们需要考虑空行在满足列的限制的情况下是否仍然满足行的限制,这个对 − 1 -1 −1 的个数讨论一下不难证得
于是可以简单地计算,时间复杂度 O ( n 2 ) O(n^2) O(n2)
#include <bits/stdc++.h>
using namespace std;
const int N=1100;
int n,m,k,dp[N][N],pw[N];
int cov1[N],cov2[N];
int od1[N],od2[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int main(){n=read(),m=read(),k=read();if((n+m)&1){ puts("0");exit(0);}for(int i=1;i<=k;i++){int x=read(),y=read(),z=read();cov1[x]++,cov2[y]++;if(z==-1) od1[x]^=1,od2[y]^=1;}int P=read();for(int i=1;i<=n;i++) if(cov1[i]==m&&!od1[i]){ puts("0");exit(0);}for(int i=1;i<=m;i++) if(cov2[i]==n&&!od2[i]){ puts("0");exit(0);}pw[0]=1;for(int i=1;i<=max(n,m);i++) pw[i]=pw[i-1]*2%P;if(n>m){for(int i=1;i<=n;i++)if(!cov1[i]){int ans=1;for(int j=1;j<=n;j++){if(i==j) continue;if(m-cov1[j]>0) ans=1ll*ans*pw[m-cov1[j]-1]%P;}printf("%d",ans);exit(0);}}elsefor(int i=1;i<=m;i++)if(!cov2[i]){int ans=1;for(int j=1;j<=m;j++){if(i==j) continue;if(n-cov2[j]>0) ans=1ll*ans*pw[n-cov2[j]-1]%P;}printf("%d",ans);exit(0);}return 0;
}CF140E
题目链接
点击打开链接
题目解法
先特殊提醒一下,每一层的球不是构成一个环,而是一个序列
可以发现这一层只关心选了几个颜色,而不关心选了那些颜色
所以显然有 d p i , j dp_{i,j} dpi,j 为到第 i i i 层,第 i i i 层有 j j j 个颜色的方案数
考虑转移
容斥一下,用总的方案数 - 不合法的方案数
所以 d p i , j = m j ‾ ∗ f l [ i ] , j ∑ d p i − 1 , k − j ! ∗ d p i − 1 , j dp_{i,j}=m^{\underline{j}}*f_{l[i],j}\sum{dp_{i-1,k}}-j!*dp_{i-1,j} dpi,j=mj∗fl[i],j∑dpi−1,k−j!∗dpi−1,j
其中 f i , j f_{i,j} fi,j 为长度为 i i i 序列,相邻不同,颜色总数为 j j j,且每一种颜色都染过的方案数
f i , j f_{i,j} fi,j 好求,不细讲了,直接给转移式子: f i , j = f i − 1 , j − 1 + f i − 1 , j ∗ ( j − 1 ) f_{i,j}=f_{i-1,j-1}+f_{i-1,j}*(j-1) fi,j=fi−1,j−1+fi−1,j∗(j−1)
因为没有规定染 m m m 个颜色中的哪 j j j 个,所以要乘 m j ‾ m^{\underline{j}} mj
减去的数中因为之前已经规定好了选哪 j j j 个,所以只需要给 j j j 个数排个次序即可(不难发现, f f f 式子中并没有规定 j j j 个颜色的顺序)
时间复杂度 O ( n 2 ) O(n^2) O(n2)
#include <bits/stdc++.h>
using namespace std;
const int MX=5100,N=1000100;
int n,m,P,l[N];
int fac[MX],perm[N];
int dp[2][MX],f[MX][MX];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int main(){n=read(),m=read(),P=read();for(int i=1;i<=n;i++) l[i]=read();fac[0]=1;for(int i=1;i<MX;i++) fac[i]=1ll*fac[i-1]*i%P;perm[0]=1;for(int i=1;i<=m;i++) perm[i]=1ll*perm[i-1]*(m-i+1)%P;f[0][0]=1;for(int i=1;i<MX;i++) for(int j=1;j<=i;j++) f[i][j]=(f[i-1][j-1]+1ll*f[i-1][j]*(j-1))%P;int sum=0;for(int i=1;i<=l[1];i++) dp[1][i]=1ll*perm[i]*f[l[1]][i]%P,sum=(sum+dp[1][i])%P;for(int i=2;i<=n;i++){for(int j=1;j<=l[i];j++) dp[i&1][j]=0;for(int j=1;j<=l[i];j++){dp[i&1][j]=1ll*perm[j]%P*sum%P*f[l[i]][j]%P;if(j<=l[i-1]) dp[i&1][j]=(dp[i&1][j]-1ll*dp[~i&1][j]*fac[j]%P*f[l[i]][j]%P+P)%P;}sum=0;for(int j=1;j<=l[i];j++) sum=(sum+dp[i&1][j])%P;}printf("%d",sum);return 0;
}CF482D
题目链接
点击打开链接
题目解法
显然树形 d p dp dp
考虑染的颜色只跟染的顺序的奇偶性有关
所以令 d p i , 0 / 1 dp_{i,0/1} dpi,0/1 表示在 i i i 的子树中,选了偶数还是奇数个点
考虑编号升序是好转移的,编号降序的方案和编号升序的方案一样
现在只需要计算编号升序和降序重复的方案数
不难发现,重复的条件为 ∀ p r e i − 1 ≡ s u f i + 1 \forall pre_{i-1}\equiv suf_{i+1} ∀prei−1≡sufi+1
可以发现这个等价于
- 每个子树中选的点都为偶数
- 每个子树中选的点都为奇数,且只有奇数个子树选到
这个可以在开一个 d p dp dp 数组 f i , 0 / 1 , 0 / 1 f_{i,0/1,0/1} fi,0/1,0/1 表示在 i i i 的子树中选出了奇数或偶数个点,所有选的子树中点数均为奇数或偶数,不难转移
时间复杂度 O ( n 2 ) O(n^2) O(n2)
#include <bits/stdc++.h>
using namespace std;
const int N=100100,P=1e9+7;
int n,dp[N][2],f[N][2][2];
vector<int> vec[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void dfs(int u){dp[u][1]=1,f[u][0][0]=f[u][0][1]=1;for(int v:vec[u]){dfs(v);int t0=dp[u][0],t1=dp[u][1];dp[u][0]=(1ll*t0*dp[v][0]+1ll*t1*dp[v][1])%P;dp[u][1]=(1ll*t0*dp[v][1]+1ll*t1*dp[v][0])%P;t0=f[u][1][1],t1=f[u][0][1];f[u][0][0]=(f[u][0][0]+1ll*f[u][0][0]*(dp[v][0]-1))%P;//子树中选了偶数个点,所有选的子树中都选了偶数个点f[u][0][1]=(f[u][0][1]+1ll*t0*dp[v][1])%P;//子树中选了偶数个点,所有选的子树中都选了奇数个点f[u][1][1]=(f[u][1][1]+1ll*t1*dp[v][1])%P;//子树中选了奇数个点,所有选的子树中都选了奇数个点}dp[u][0]=(dp[u][0]*2+1)%P,dp[u][1]=dp[u][1]*2%P;dp[u][0]=(dp[u][0]-f[u][1][1]+P)%P,dp[u][1]=(dp[u][1]-f[u][0][0]+P)%P;
}
int main(){n=read();for(int i=2;i<=n;i++) vec[read()].push_back(i);dfs(1);printf("%d",(dp[1][0]+dp[1][1]-1)%P);return 0;
}CF325E
题目链接
点击打开链接
题目解法
先考虑 n n n 为偶数的情况
先看一个比较妙的性质:对于 i i i 和 i + n 2 i+\frac{n}{2} i+2n,它们能到达的两个点是一样的,因为 2 i ≡ 2 i + n 2i\equiv2i+n 2i≡2i+n 且 2 i + 1 ≡ 2 i + n + 1 2i+1\equiv 2i+n+1 2i+1≡2i+n+1
所以考虑暂时钦定 i i i 连向 2 i 2i 2i, i + n 2 i+\frac{n}{2} i+2n 连向 2 i + 1 2i+1 2i+1
考虑这样整张图会形成若干个简单环,现在需要考虑合并简单环
若 x x x 和 x + n 2 x+\frac{n}{2} x+2n 不在一个简单环内,那么考虑把 x x x 连到 2 x + 1 2x+1 2x+1, x + n 2 x+\frac{n}{2} x+2n 连到 2 x 2x 2x,这样可以把 2 2 2 个环合并成一个环,这个可以用并查集维护
考虑 n n n 为奇数的情况,直觉告诉我们一定是无解的
考虑来证明它:可以发现到终点 0 0 0 的点只能是 n − 1 2 \frac{n-1}{2} 2n−1,而到达 n − 1 n-1 n−1 的点也只能是 n − 1 2 \frac{n-1}{2} 2n−1,这就矛盾了
时间复杂度 O ( n ) O(n) O(n)
#include <bits/stdc++.h>
using namespace std;
const int N=100100;
int n,fa[N],rt,nxt[N];
bool vis[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void dfs(int u){vis[u]=1,fa[u]=rt;if(!vis[nxt[u]]) dfs(nxt[u]);
}
int get_father(int x){ return x==fa[x]?x:fa[x]=get_father(fa[x]);}
int main(){n=read();if(n&1){ puts("-1");exit(0);}for(int i=0;i<n/2;i++) nxt[i]=i<<1,nxt[i+n/2]=i<<1^1;for(int i=0;i<n;i++) fa[i]=i;for(int i=0;i<n;i++) if(!vis[i]) rt=i,dfs(i);for(int i=0;i<n/2;i++){int x=get_father(i),y=get_father(i+n/2);if(x!=y) fa[x]=y,nxt[i]=i<<1^1,nxt[i+n/2]=i<<1;}int pos=0;while(nxt[pos]) printf("%d ",pos),pos=nxt[pos];printf("%d 0",pos);return 0;
}CF896D
题目链接
点击打开链接
题目解法
先考虑 n n n 个人不包含 v i p vip vip 的情况
考虑转化,把 50 50 50 元看成 1 1 1, 100 100 100 元看成 − 1 -1 −1
题目就是问有多少种方案,所有的前缀和都 ≥ 0 \ge 0 ≥0
这让我们想到了卡特兰数,于是可以考虑用推卡特兰数的方法来推到 ( x , n − x ) (x,n-x) (x,n−x) 处的方案数,条件是 n − x + l ≤ x ≤ n − x + r n-x+l\le x\le n-x+r n−x+l≤x≤n−x+r
推断方法不细讲,大概就是对 y = x + 1 y=x+1 y=x+1 作对称,最后推出来的式子应该是 ( n x ) − ( n x + 1 ) \binom{n}{x}-\binom{n}{x+1} (xn)−(x+1n)
然后考虑有 v i p vip vip 的情况,即枚举个数,最终的答案即为 ∑ i = 0 n ∑ i − x + l ≤ x ≤ i − x + r ( i x ) − ( i x + 1 ) \sum\limits_{i=0}^{n}\sum\limits_{i-x+l\le x\le i-x+r}\binom{i}{x}-\binom{i}{x+1} i=0∑ni−x+l≤x≤i−x+r∑(xi)−(x+1i)
可以发现对于同一个 i i i,中间的组合数都可以消掉,所以只要算最左边和最右边的组合数即可
考虑 P P P 不是质数,我们可以把 p p p 质因数分解,然后把每个计算的数拆分成 x ∗ ∏ p k α k x*\prod p_k^{\alpha_k} x∗∏pkαk,其中 ( x , P ) = 1 (x,P)=1 (x,P)=1,这个对每个 p p p 的质因子开个桶即可,考虑 P P P 的质因子不会超过 9 个,所以可以很快维护
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=100100;
int n,P,l,r;
int phi,pr[N],cnt;
int fac[N],invX[N],coef[N][35];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int qmi(int a,int b){int res=1;for(;b;b>>=1){if(b&1) res=1ll*res*a%P;a=1ll*a*a%P;}return res;
}
void calc(){fac[0]=invX[0]=1,fac[1]=invX[1]=1;for(int i=2;i<=n;i++){int t=i;for(int j=1;j<=cnt;j++){coef[i][j]=coef[i-1][j];while(t%pr[j]==0) t/=pr[j],coef[i][j]++;}fac[i]=1ll*fac[i-1]*t%P;invX[i]=qmi(fac[i],phi-1);}
}
int binom(int x,int y){if(x<y) return 0;int res=fac[x]*invX[y]%P*invX[x-y]%P;for(int i=1;i<=cnt;i++) res=res*qmi(pr[i],coef[x][i]-coef[y][i]-coef[x-y][i])%P;return res;
}
signed main(){n=read(),P=read(),l=read(),r=read();phi=P;int t=P;for(int i=2;i*i<=t;i++)if(t%i==0){while(t%i==0) t/=i;pr[++cnt]=i,phi=phi/i*(i-1);}if(t>1) pr[++cnt]=t,phi=phi/t*(t-1);calc();int ans=0;for(int i=0;i<=n;i++){int lb=(l+i+1)/2;int rb=min((r+i)/2,i);if(lb<=rb) ans=(ans+(binom(i,lb)-binom(i,rb+1)+P)*binom(n,i)%P)%P;}printf("%lld",ans);return 0;
}CF750G
题目链接
点击打开链接
题目解法
考虑对答案的路径分 3 种情况
- 一个点,方案数为 1
- 从祖先到子孙的路径
令祖先的编号为 u u u,延续到下面的深度为 h h h
则编号和为 ( 2 h + 1 − 1 ) ∗ u + ∑ i = 0 h − 1 ( 2 i − 1 ) ∗ c i (2^{h+1}-1)*u+\sum_{i=0}^{h-1} (2^i-1)*c_i (2h+1−1)∗u+∑i=0h−1(2i−1)∗ci,其中 c i c_i ci 为这条边是否往右走
考虑 ∑ i = 0 h − 1 2 i ∗ c i < 2 h \sum_{i=0}^{h-1} 2^i*c_i<2^h ∑i=0h−12i∗ci<2h,那么枚举 h h h,我们可以直接计算出对应的 u u u
然后判断是否合法即可 - 从 u u u 到 l c a lca lca 到 v v v 的路径( u ≠ l c a ≠ v u\neq lca\neq v u=lca=v)
令祖先的编号为 u u u,延续到下面的深度分别为 h 1 , h 2 h1,h2 h1,h2
则编号和为 ( 2 h 1 + 1 + 2 h 2 + 1 − 2 ) ∗ u + ∑ i = 0 h 1 − 1 ( 2 i − 1 ) c i + ∑ i = 0 h 2 − 1 ( 2 i − 1 ) c i ′ (2^{h1+1}+2^{h2+1}-2)*u+\sum_{i=0}^{h1-1}(2^i-1)c_i+\sum_{i=0}^{h2-1}(2^i-1)c'_i (2h1+1+2h2+1−2)∗u+∑i=0h1−1(2i−1)ci+∑i=0h2−1(2i−1)ci′
同理对于相同的 h 1 , h 2 h1,h2 h1,h2,我们可以唯一确定出一个 u u u
那么考虑计算下面有多少种路径
考虑 2 i − 1 2^i-1 2i−1 的 − 1 -1 −1 不好计算,所以考虑枚举 c i , c i ′ c_i,c'_i ci,ci′ 为 1 1 1 的数的个数
然后考虑 d p dp dp,令 d p i , j , 0 / 1 dp_{i,j,0/1} dpi,j,0/1 表示从低到高到了第 i i i 位,已经选了 j j j 个数,是否进位的方案数
这样可以轻松转移,要注意 h 1 − 1 h1-1 h1−1 和 h 2 − 1 h2-1 h2−1 位要强制选和不选(因为必须往左和往右)
时间复杂度 O ( H 5 ) O(H^5) O(H5), H H H 为树高
#include <bits/stdc++.h>
#define int long long
using namespace std;
int s,bs[60],dp[60][120][2];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int check(int left,int h){for(int i=h;i>=0;i--) if(left>=bs[i]-1) left-=bs[i]-1;return !left;
}
int calc(int h1,int h2,int left){int res=0;for(int i=1;i<=h1+h2;i++){int curleft=left+i;bool flg=1;for(int j=max(h1,h2)+2;j<=50;j++) if(curleft>>j&1){ flg=0;break;}if(!flg||(curleft&1)) continue;memset(dp,0,sizeof(dp));dp[0][0][0]=1;for(int j=1;j<=max(h1,h2)+1;j++)for(int k=0;k<=i;k++)for(int z=0;z<=1;z++){if(!dp[j-1][k][z]) continue;for(int x=0;x<=(j<h1);x++)for(int y=(j==h2);y<=(j<=h2);y++){int curbit=(x+y+z)%2,ne=(x+y+z)/2;if(curbit!=(curleft>>j&1ll)) continue;dp[j][k+x+y][ne]+=dp[j-1][k][z];}}res+=dp[max(h1,h2)+1][i][0];}return res;
}
signed main(){s=read();bs[0]=1;for(int i=1;i<=51;i++) bs[i]=bs[i-1]*2;int ans=1;//选n//端点u,v为祖孙关系//枚举相差层数for(int h=1;h<=50;h++){int u=s/(bs[h+1]-1);//头if(!u) continue;if(check(s-u*(bs[h+1]-1),h)) ans++;}//端点u,v不是祖孙关系for(int h1=1;h1<=50;h1++)for(int h2=1;h2<=50;h2++){int u=s/(bs[h1+1]+bs[h2+1]-3);if(!u) continue;ans+=calc(h1,h2,s-u*(bs[h1+1]+bs[h2+1]-3));}printf("%lld",ans);return 0;
}
/*
dp[i][j][0/1]:到第i位,选了j个数,是否有进位的方案数
*/
CF981H
题目链接
点击打开链接
题目解法
感觉挺好的一道题,除了多项式
显然 k k k 条路径共同经过的部分一定是一段路径
然后考虑分类讨论路径端点 u , v u,v u,v 的关系
- u , v u,v u,v 不是祖先关系
答案即为 s u × s v s_u\times s_v su×sv
其中 s u s_u su 表示在 u u u 的子树中选出 k k k 个点,并组成排列的方案数
考虑枚举 u u u 节点的选择个数,因为只有它是可以经过不限制次的, u u u 的儿子的子树中只能选出 1 1 1 个点
所以考虑除了 u u u 选 i i i 个点且不考虑顺序的方案数即为 [ x i ] ∏ ( 1 + s i z v x ) [x^i]\prod (1+siz_vx) [xi]∏(1+sizvx)
因为是要求出这个多项式卷积的每一项的,所以考虑用分治 n t t ntt ntt 求出
然后 s u s_u su 即为 ∑ i = 0 k ( k i ) × i ! × [ x i ] ∏ ( 1 + s i z v x ) \sum\limits_{i=0}^{k}\binom{k}{i}\times i!\times [x^i]\prod (1+siz_vx) i=0∑k(ik)×i!×[xi]∏(1+sizvx)
然后所有情况的答案即为 ( ∑ s u ) 2 (\sum s_u)^2 (∑su)2
还需要减去 u u u 和 u u u 自己的代价和 u u u 和 u u u 的子树内的点的代价
这用一个子树和不难求出 - u , v u,v u,v 是祖先关系
这种情况稍微难办一些
不考虑 u u u 选出 i i i 个点的方案数为 [ x i ] ∑ v ∈ s o n ( u ) ( 1 + ( n − s i z u ) x ) × ∏ w ≠ v ( 1 + s i z w x ) [x^i]\sum\limits_{v\in son(u)}{(1+(n-siz_u)x)\times \prod\limits_{w\neq v} (1+siz_wx)} [xi]v∈son(u)∑(1+(n−sizu)x)×w=v∏(1+sizwx)
这个也可以用分治 n t t ntt ntt 求出
计算答案的式子和第一类情况一样
记得特判一条路径的情况
因为度数之和为 n n n,所以时间复杂度是分治 n t t ntt ntt 的 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
#include <bits/stdc++.h>
using namespace std;
const int N=300000,P=998244353;
const int G=3,Gi=332748118;
typedef pair<vector<int>,vector<int> > pvv;
typedef pair<int,int> pii;
int n,k,ans,ans2;
int rev[N],tot;
int f[N],s[N];
int siz[N],fac[N],inv[N];
vector<pii> son;
vector<int> vec[N],Gr[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline void inc(int &x,int y){x+=y;if(x>=P) x-=P;
}
int qmi(int a,int b){int res=1;for(;b;b>>=1){if(b&1) res=1ll*res*a%P;a=1ll*a*a%P; }return res;
}
vector<int> ntt(vector<int> a,bool neg){for(int i=0;i<tot;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);for(int mid=1;mid<tot;mid<<=1){int g1=qmi(neg?Gi:G,(P-1)/(mid<<1));for(int i=0;i<tot;i+=mid<<1){int gk=1;for(int j=0;j<mid;j++,gk=1ll*gk*g1%P){int x=a[i+j],y=1ll*gk*a[i+j+mid]%P;a[i+j]=x+y>=P?x+y-P:x+y,a[i+j+mid]=x-y<0?x-y+P:x-y;}}}return a;
}
vector<int> mul(vector<int> A,vector<int> B){int bit=0;while((1<<bit)<=A.size()+B.size()) bit++;tot=1<<bit;for(int i=0;i<tot;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));A.resize(tot),B.resize(tot);A=ntt(A,0),B=ntt(B,0);for(int i=0;i<tot;i++) A[i]=1ll*A[i]*B[i]%P;A=ntt(A,1);int iv=qmi(tot,P-2);for(int i=0;i<tot;i++) A[i]=1ll*A[i]*iv%P;while(!A.back()) A.pop_back();return A;
}
vector<int> add(vector<int> A,vector<int> B)if(A.size()<B.size()) swap(A,B);for(int i=0;i<B.size();i++) inc(A[i],B[i]);return A;
}
pvv pushup(pvv L,pvv R){vector<int> f=mul(L.first,R.first);vector<int> g=add(mul(L.first,R.second),mul(L.second,R.first));return make_pair(f,g);
}
pvv solve(int l,int r){if(l==r) return make_pair(vector<int>{1,son[l].first},vector<int>{son[l].second});int mid=(l+r)>>1;return pushup(solve(l,mid),solve(mid+1,r));
}
void predfs(int u,int fa){siz[u]=1;for(int v:vec[u])if(v!=fa){predfs(v,u);siz[u]+=siz[v],Gr[u].push_back(v);}
}
int C(int a,int b){ return 1ll*fac[a]*inv[b]%P*inv[a-b]%P;}
void dfs(int u){for(int v:Gr[u]) dfs(v),inc(s[u],s[v]);if(!Gr[u].size()) f[u]=s[u]=1;else{son.clear();for(int v:Gr[u]) son.push_back({siz[v],s[v]});pvv ret=solve(0,son.size()-1);vector<int> poly1=ret.first,poly2=ret.second;for(int i=0;i<min((int)poly1.size(),k+1);i++) inc(f[u],1ll*poly1[i]*C(k,i)%P*fac[i]%P);inc(s[u],f[u]);poly2=mul(vector<int>{1,n-siz[u]},poly2);for(int i=0;i<min((int)poly2.size(),k+1);i++) inc(ans2,1ll*poly2[i]*C(k,i)%P*fac[i]%P);}inc(ans,P-1ll*f[u]*(2*s[u]%P-f[u]+P)%P);
}
int main(){n=read(),k=read();if(k==1){ printf("%d\n",(1ll*n*(n-1)/2)%P);exit(0);fac[0]=1;for(int i=1;i<=n+1;i++) fac[i]=1ll*fac[i-1]*i%P;inv[n+1]=qmi(fac[n+1],P-2);for(int i=n;i>=0;i--) inv[i]=1ll*inv[i+1]*(i+1)%P;for(int i=1;i<n;i++){int x=read(),y=read();vec[x].push_back(y),vec[y].push_back(x);}predfs(1,-1),dfs(1);inc(ans,1ll*s[1]*s[1]%P),ans=1ll*ans*qmi(2,P-2)%P;inc(ans,ans2);printf("%d\n",ans);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}CF698F
题目链接
点击打开链接
题目解法
不是很想写,一些结论我也说不清楚也不会证,自己看题解吧
有时间可能会补,先给出代码:
#include <bits/stdc++.h>
using namespace std;
const int N=1000100,P=1e9+7;
int n,p[N],dy1[N],dy2[N],c1[N],c2[N];
int mulp[N],fac[N],chu[N];
int pr[N],v[N],cnt;
vector<int> factor[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int main(){n=read();for(int i=1;i<=n;i++) mulp[i]=1;c1[1]++;factor[1].push_back(1),chu[1]=1;for(int i=2;i<=n;i++){if(!v[i]){pr[++cnt]=i,chu[i]=n/i,c1[n/i]++;for(int j=i;j<=n;j+=i) factor[j].push_back(i),mulp[j]*=i;}for(int j=1;j<=cnt&&pr[j]<=n/i;j++){v[pr[j]*i]=pr[j];if(v[i]==pr[j]) break;}}for(int i=1;i<=n;i++) c2[mulp[i]]++;for(int i=1;i<=n;i++) p[i]=read();for(int i=1;i<=n;i++){if(!p[i]) continue;if(factor[i].size()!=factor[p[i]].size()){ puts("0");exit(0);}for(int j=0;j<factor[i].size();j++) if(chu[factor[i][j]]!=chu[factor[p[i]][j]]){ puts("0");exit(0);}int mxfac1=factor[i].back(),mxfac2=factor[p[i]].back();if(dy1[mxfac1]&&dy1[mxfac1]!=mxfac2){ puts("0");exit(0);}if(dy2[mxfac2]&&dy2[mxfac2]!=mxfac1){ puts("0");exit(0);}if(!dy1[mxfac1]&&!dy2[mxfac2]) c1[chu[mxfac1]]--;dy1[mxfac1]=mxfac2,dy2[mxfac2]=mxfac1;c2[mulp[p[i]]]--;}fac[0]=1;for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%P;int ans=1;for(int i=1;i<=n;i++) ans=1ll*ans*fac[c1[i]]%P*fac[c2[i]]%P;printf("%d",ans);return 0;
}相关文章:

组合计数训练题解
CF40E 题目链接 点击打开链接 题目解法 首先,如果 n , m n,m n,m 一奇一偶,那么答案为 0 0 0 原因是从行和列的角度分析, − 1 -1 −1 个数的奇偶性不同 可以发现 k < max { n , m } k<\max\{n,m\} k<max{n,m} 的性质很微…...

P1095 [NOIP2007 普及组] 守望者的逃离
[NOIP2007 普及组] 守望者的逃离 - 洛谷 首先DP的套路就是先找状态 这题也找不出其他的状态了,只有时间一个 所以用f[i]表示时刻i能走多远 而仔细一想实际上决策只有跑、闪现、停三种决策 然而闪现的耗蓝要和跑步一同计算十分麻烦 于是把它们分开算࿱…...

Python函数绘图与高等代数互融实例(八):箱线图|误差棒图|堆积图
Python函数绘图与高等代数互融实例(一):正弦函数与余弦函数 Python函数绘图与高等代数互融实例(二):闪点函数 Python函数绘图与高等代数互融实例(三):设置X|Y轴|网格线 Python函数绘图与高等代数互融实例(四):设置X|Y轴参考线|参考区域 Python函数绘图与高等代数互融实例(五…...
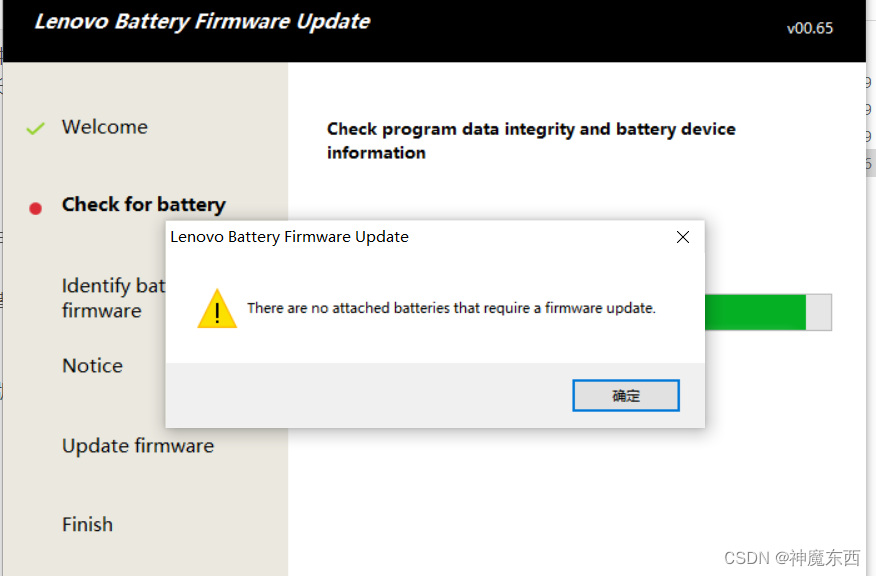
联想y7000 y7000p 2018/2019 不插电源 不插充电器, 直接关机 ,电量一直89%/87%/86%,V0005如何解决?
这种问题,没有外力破坏的话,电池不可能突然出事。这种一般是联想的固件问题,有可能发生在系统更新,或者突然的不正常关机或长时间电池过热,原因我不是很清楚。 既然发生了,根据我收集的解决方法,…...

stm32与esp8266通信
esp8266 #include <ESP8266WiFi.h> #include <ESP8266HTTPClient.h>// 测试HTTP请求用的URL // #define URL "http://162.14.107.118:8086/PC/modifyFoodPrice/0/6"// 测试HTTP请求用的URL // 设置wifi接入信息(请根据您的WiFi信息进行修改) const char…...

组合数 2.1 2.2
O(nlogn)预处理, O(1)查询 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \nusing namespace std;typedef pair<int, int> PII; typedef long long ll; typedef long double ld;const int N 1000…...

【数组的中心位置】python实现-附ChatGPT解析
1.题目 数组的中心位置 题目 给你一个整数数组 nums,请计算数组的中心位置。 数组中心位置是数组的一个下标,其左侧所有元素相乘的积等于右侧所有元素相乘的积。 数组第一个元素的左侧积为 1,最后一个元素的右侧积为 1。 如果数组有多个中心位置,应该返回最靠近左边的那一个…...

黑马JVM总结(二十三)
(1)字节码指令-init 方法体内有一些字节,对应着将来要由java虚拟机执行方法内的代码,构造方法里5个字节代码,main方法里有9个字节的代码 java虚拟机呢内部有一个解释器,这个解释器呢可以识别平台无关的字…...
AI人体行为分析:玩手机/打电话/摔倒/攀爬/扭打检测及TSINGSEE场景解决方案
一、AI人体行为分析技术概述及场景 人体姿态分析/行为分析/动作识别AI算法,是一种利用人工智能技术对人体行为进行检测、跟踪和分析的方法。通过计算机视觉、深度学习和模式识别等技术,可以实现对人体姿态、动作和行为的自动化识别与分析。 在场景应用…...

HI_NAS linux 记录
dev/root 100% 占用解决记录 通过下面的命令查看各文件夹 大小 sudo du --max-depth1 -h # 统计当前文件夹下各个文件夹的大小显示为M 最终发现Var/log 占用很大空间 发现下面两个 log 占用空间很大,直接 rm-rf 即可 HI NAS python3 记录 # 安装pip3 sudo apt u…...
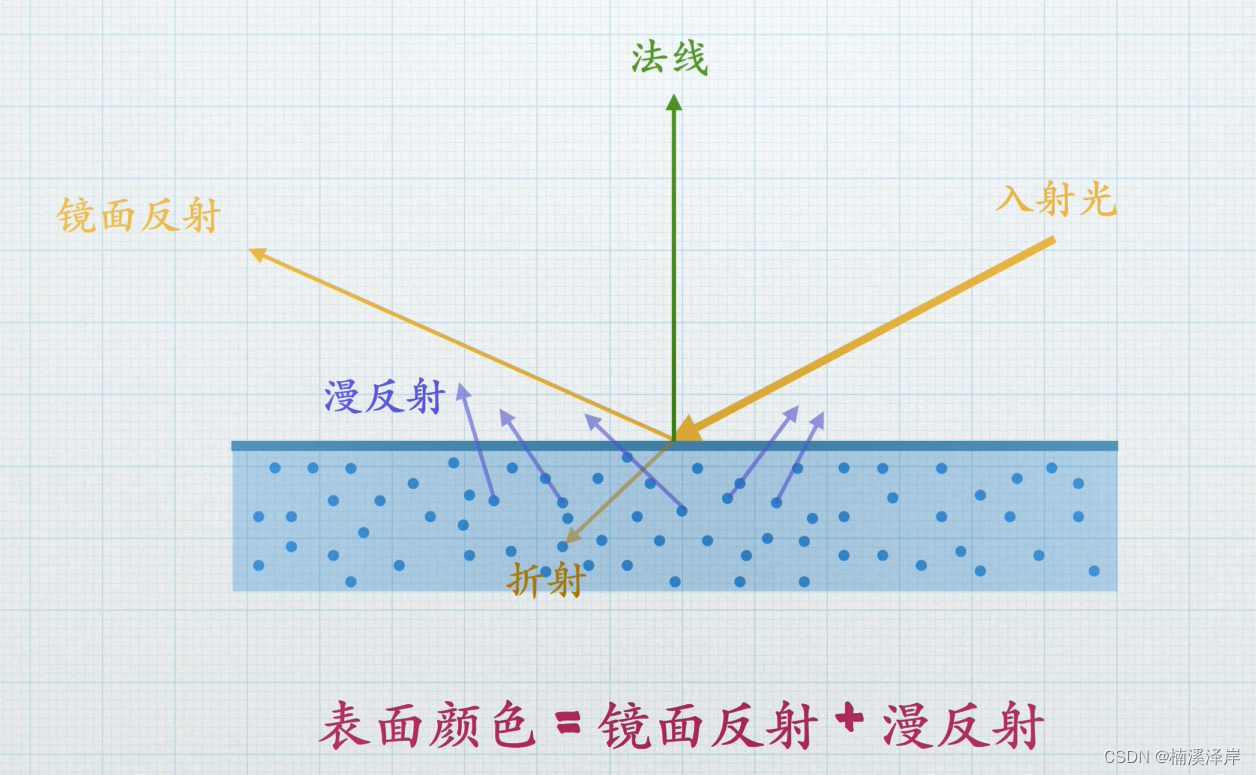
计算机图形学中的几何光学
文章目录 前言一、图形学中的光学二、光照模型1、经验型(简单)2、物理型(复杂) 前言 在学习Shader光照之前了解一下计算机图形学 一、图形学中的光学 镜面反射的效果例子:物体表面高光 慢反射的效果的例子:…...
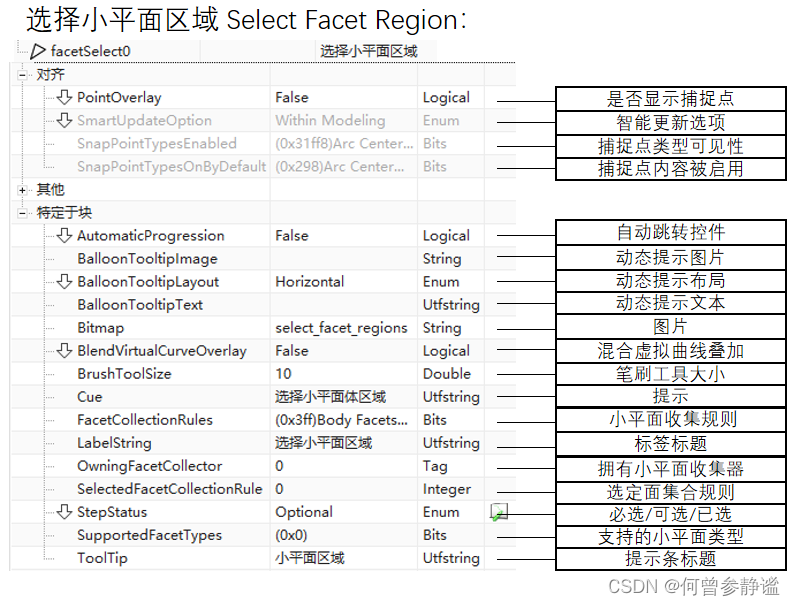
「UG/NX」BlockUI 选择小平面区域 Select Facet Region
✨博客主页何曾参静谧的博客📌文章专栏「UG/NX」BlockUI集合📚全部专栏「UG/NX」NX二次开发「UG/NX」BlockUI集合「VS」Visual Studio「QT」QT5程序设计「C/C」C/C程序设计「Win」Windows程序设计「DSA」数据结构与算法「File」数据文件格式 目录 控件说…...

【完全二叉树魔法:顺序结构实现堆的奇象】
本章重点 二叉树的顺序结构堆的概念及结构堆的实现堆的调整算法堆的创建堆排序TOP-K问题 1.二叉树的顺序结构 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构…...

Maven官方镜像仓库与阿里云云效Maven
一、Maven官方镜像仓库 download maven-3 右击复制链接地址,使用wget命令直接在linux中下载: wget 链接地址history 二、阿里云云效Maven 详情查看maven 配置指南 打开 maven 的配置文件( windows 机器一般在 maven 安装目录的 conf/…...

python系列教程215——列表解析与矩阵
朋友们,如需转载请标明出处:https://blog.csdn.net/jiangjunshow 声明:在人工智能技术教学期间,不少学生向我提一些python相关的问题,所以为了让同学们掌握更多扩展知识更好地理解AI技术,我让助理负责分享…...
fonts什么文件夹可以删除吗?fonts文件夹删除了怎么恢复
在电脑上,fonts文件夹是存放字体文件的目录之一。尽管有时可能考虑删除该文件夹以节省硬盘空间或出于其他原因,但删除该文件夹可能会导致系统字体问题,影响用户的正常使用。因此,在删除之前需要考虑是否可以删除fonts文件夹&#…...
【智慧工地源码】智慧工地助力数字建造、智慧建造、安全建造、绿色建造
智慧工地围绕建设过程管理,建设项目与智能生产、科学管理建设项目信息生态系统集成在一起,该数据在虚拟现实环境中,将物联网收集的工程信息用于数据挖掘和分析,提供过程趋势预测和专家计划,实现工程建设的智能化管理&a…...

CListCtrl设置只显示单列
CListCtrl设置只显示单列 2023/9/5 下午4:07:15 要将CListCtrl控件设置为只显示单列,您可以使用SetExtendedStyle函数来设置控件的样式。下面是设置只显示单列的示例代码: cpp m_listCtrl.SetExtendedStyle(LVS_EX_GRIDLINES | LVS_EX_FULLROWSELECT | LVS_EX_HEADERDRAG…...

冒泡排序与选择排序(最low的两兄弟)
个人主页:Lei宝啊 愿所有美好如期而遇 前言: 在我们的生活中,无处不在用到排序,比如说成绩的排名,淘宝,京东等等商品在各个方面的排序,这样看来一个好的算 法很重要,接下来我们要先…...

MySQL-三大日志
前言 redo log:为了持久化数据,当内存中的数据还没写入到磁盘而宕机时,会读取该日志持久化数据到磁盘 undo log:为了保证原子性,事务的操作都会记录一条相反的sql到该日志,出现错误就会根据该文件恢…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
