深入浅出C++ ——手撕红黑树
文章目录
- 一、红黑树的概念
- 二、红黑树的性质
- 三、红黑树节点的定义
- 四、红黑树的插入操作
- 五、红黑树的验证
- 五、红黑树的删除
- 六、红黑树与AVL树的比较
- 七、红黑树的应用
- 八、红黑树模拟实现
一、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

二、红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的,即树中没有连续的红色节点
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点,即每条路径的黑色节点数量相等
- 每个叶子结点(这里的叶子结点指的是空结点,也叫做NIL节点 )都是黑色的
红黑树中第三和第四条规则构成互斥,极限的最短一定是全黑,极限的最长一定是一黑一红 。
三、红黑树节点的定义
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv){}pair<K, V> _kv; //节点的值域Colour _col; //节点的颜色RBTreeNode<K, V>* _left; //节点的左孩子RBTreeNode<K, V>* _right; //节点的右孩子RBTreeNode<K, V>* _parent; //节点的双亲
};
四、红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:一、按照二叉搜索的树规则插入新节点。二、检测新节点插入后,红黑树的性质是否造到破坏。
因为新节点的默认颜色是红色,如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三(不能有连续的红色节点),此时需要对红黑树分情况来讨论。
情况一: cur为红,p为红,g为黑,u存在且为红
cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点。此处看到的树,可能是一颗完整的树,但是也有可能是一颗子树。
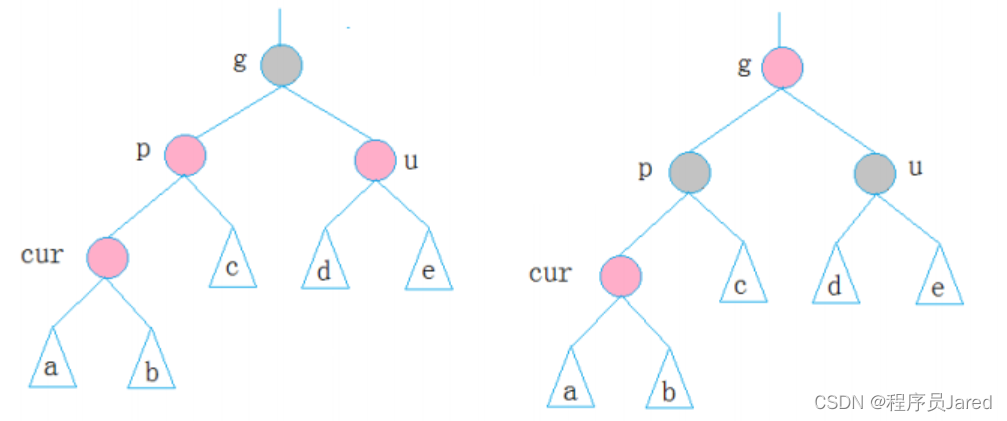
解决方式是将将p,u改为黑,g改为红。继续把g当成cur,g是根节点,需要将g改为黑色,如果g是子树且g的双亲颜色为红色,则需要继续向上调整。
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑
如果u节点不存在,那么cur一定为新插入的节点,否则就违反性质4。如果u节点存在,则一定是黑色的,cur之前也是黑色的,因为新增节点是a、b节点,所以现在它是红色。
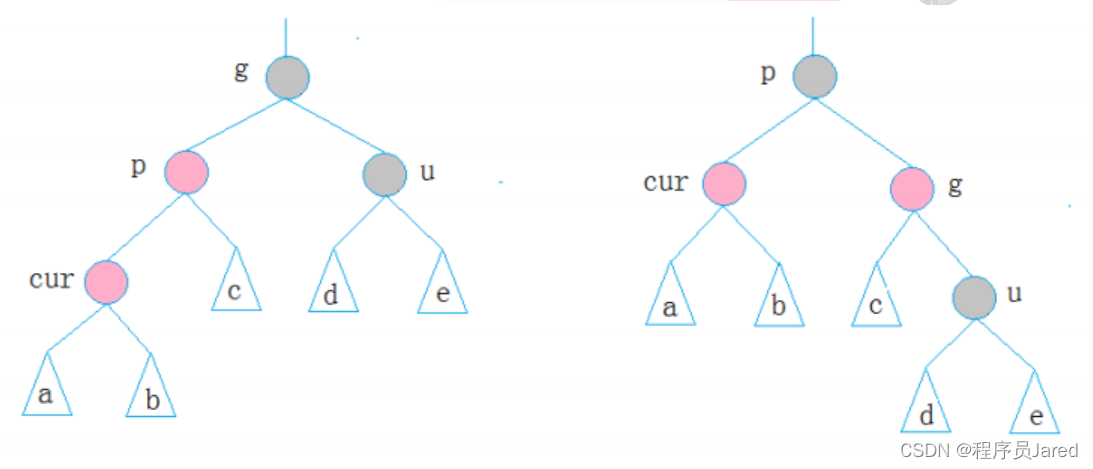
解决方式:如果p为g的左孩子,cur为p的左孩子,则进行右单旋转;p为g的右孩子,cur为p的右孩子,则进行左单旋转。然后再将p变黑,g变红。
情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑
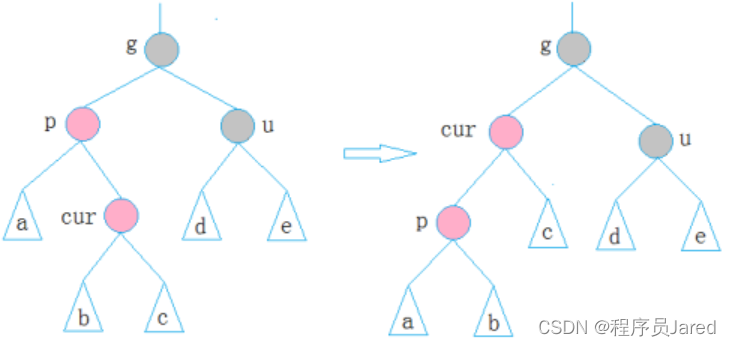
解决方式:如果p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;如果p为g的右孩子,cur为p的左孩子,则针对p做右单旋转。旋转后就转变为了情况二。
总结
在这三种情况中,都有cur为红,p为红,g为黑,可以看出红黑树的关键是叔叔。U存在且为红则变色继续往上处理,U不存在或为黑,则旋转加变色。
情况二和情况三的主要区别是单旋和双旋的不同。从图中可以看出,当p g cur为一条直线的时候,也就是情况二,单旋即可;p g cur 为一条折线的时候,也就是情况三,需要双旋。
代码实现
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur) //找插入位置{if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);//新节点的默认颜色是红色,因为如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfater = parent->_parent;assert(grandfater);assert(grandfater->_col == BLACK);// 关键看叔叔if (parent == grandfater->_left){Node* uncle = grandfater->_right;// 情况一 : uncle存在且为红,变色+继续往上处理if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;// 继续往上处理cur = grandfater;parent = cur->_parent;}// 情况二+三:uncle不存在 + 存在且为黑else{// 情况二:右单旋+变色// g // p u// cif (cur == parent->_left){RotateR(grandfater);parent->_col = BLACK;grandfater->_col = RED;}else{// 情况三:左右单旋+变色// g // p u// cRotateL(parent);RotateR(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}else // (parent == grandfater->_right){Node* uncle = grandfater->_left;// 情况一if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;// 继续往上处理cur = grandfater;parent = cur->_parent;}else{// 情况二:左单旋+变色// g // u p// cif (cur == parent->_right){RotateL(grandfater);parent->_col = BLACK;grandfater->_col = RED;}else{// 情况三:右左单旋+变色// g // u p// cRotateR(parent);RotateL(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}}_root->_col = BLACK;return true;
}
五、红黑树的验证
红黑树的检测分为两步:一、检测其是否满足二叉搜索树,这里只需要中序遍历是否为有序序列即可。二、检测其是否满足红黑树的性质。
public:bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col == RED){cout << "根节点不是黑色" << endl;return false;}int benchmark = 0;return PrevCheck(_root, 0, benchmark);}
private:bool PrevCheck(Node* root, int blackNum, int& benchmark){if (root == nullptr){if (benchmark == 0){benchmark = blackNum;return true;}if (blackNum != benchmark){cout << "某条黑色节点的数量不相等" << endl;return false;}else{return true;}}if (root->_col == BLACK){++blackNum;}if (root->_col == RED && root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}return PrevCheck(root->_left, blackNum, benchmark)&& PrevCheck(root->_right, blackNum, benchmark);}
五、红黑树的删除
红黑树的删除过于复杂,可以参考 红黑树的删除 这篇博客
六、红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log2Nlog_2 Nlog2N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
七、红黑树的应用
红黑树的应用场景建议观看这个视频讲解红黑树在linux中的3种应用场景
八、红黑树模拟实现
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv){}pair<K, V> _kv;Colour _col;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;
};template<class K, class V>
struct RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur) //找插入位置{if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);//新节点的默认颜色是红色,因为如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfater = parent->_parent;assert(grandfater);assert(grandfater->_col == BLACK);// 关键看叔叔if (parent == grandfater->_left){Node* uncle = grandfater->_right;// 情况一 : uncle存在且为红,变色+继续往上处理if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;// 继续往上处理cur = grandfater;parent = cur->_parent;}// 情况二+三:uncle不存在 + 存在且为黑else{// 情况二:右单旋+变色// g // p u// cif (cur == parent->_left){RotateR(grandfater);parent->_col = BLACK;grandfater->_col = RED;}else{// 情况三:左右单旋+变色// g // p u// cRotateL(parent);RotateR(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}else // (parent == grandfater->_right){Node* uncle = grandfater->_left;// 情况一if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfater->_col = RED;// 继续往上处理cur = grandfater;parent = cur->_parent;}else{// 情况二:左单旋+变色// g // u p// cif (cur == parent->_right){RotateL(grandfater);parent->_col = BLACK;grandfater->_col = RED;}else{// 情况三:右左单旋+变色// g // u p// cRotateR(parent);RotateL(grandfater);cur->_col = BLACK;grandfater->_col = RED;}break;}}}_root->_col = BLACK;return true;}void InOrder(){_InOrder(_root);cout << endl;}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col == RED){cout << "根节点不是黑色" << endl;return false;}// 黑色节点数量基准值int benchmark = 0;return PrevCheck(_root, 0, benchmark);}private:bool PrevCheck(Node* root, int blackNum, int& benchmark){if (root == nullptr){if (benchmark == 0){benchmark = blackNum;return true;}if (blackNum != benchmark){cout << "某条黑色节点的数量不相等" << endl;return false;}else{return true;}}if (root->_col == BLACK){++blackNum;}if (root->_col == RED && root->_parent->_col == RED){cout << "存在连续的红色节点" << endl;return false;}return PrevCheck(root->_left, blackNum, benchmark)&& PrevCheck(root->_right, blackNum, benchmark);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}
private:Node* _root = nullptr;
};
相关文章:

深入浅出C++ ——手撕红黑树
文章目录一、红黑树的概念二、红黑树的性质三、红黑树节点的定义四、红黑树的插入操作五、红黑树的验证五、红黑树的删除六、红黑树与AVL树的比较七、红黑树的应用八、红黑树模拟实现一、红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存…...
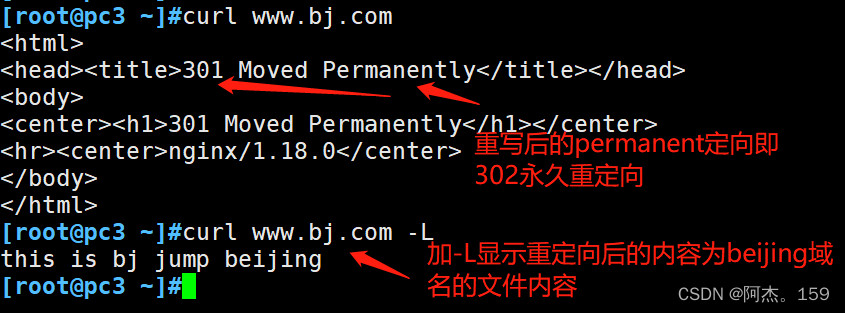
Linux服务:Nginx服务重写功能
目录 一、重写功能 1、重写功能作用 2、rewrite指令 ①if指令 ②return指令 ③ set指令 ④break指令 3、rewrite标志 ①redirect标志 ②permanent标志 ③break标志 ④last标志 ⑤rewrite标志实验 一、重写功能 1、重写功能作用 重写功能(rewrite)用于实现URL的重…...

3.知识图谱概念和相关技术简介[知识抽取、知识融合、知识推理方法简述],典型应用案例介绍国内落地产品介绍。一份完整的入门指南,带你快速掌握KG知识,芜湖起飞!
1. 知识图谱(KG)的概念 知识图谱(KG)得益于Web的发展(更多的是数据层面),有着来源于KR、NLP、Web、AI多个方面的基因。知识图谱是2012年后的提法,基础还是语义网和本体论。 知识图谱的本质包含: 知识表示——Knowledge Representation基于知识表示的知识库——Knowledge…...

iOS 绿幕技术
绿幕(green screen)技术,又称 chroma key effect,实际上是将图片上指定颜色设置为透明的图形处理技术,这些透明区域也可以被任意背景图片替换。 这种技术在 视频合成中被广泛使用。iOS 中,通过 CoreImage …...
git 的使用方法(上 - 指令)
目录前言:一、Git 是什么?二、SVN与Git的最主要的区别?三、Git 安装四、git 配置1. 创建仓库 - repository2. 配置3. 工作流与基本操作五、Git 的使用流程1. 仓库中创建 1.txt文件2. 查看工作区的文件状态3. 添加工作区文件到暂存区4. 创建版…...

Windows 平台 oracle11g 单机 打补丁(33883353)
一、从oracle官网下载最新补丁包和打包工具 二、 对数据库及软件作全备 略 三、解压p33883353_112040_MSWIN-x86-64.zip 在33883353文件夹中打开README.html 2.1 OPatch Utility You must use the OPatch utility version 11.2.0.3.34 or later to apply this patch. 必须…...

1个寒假能学会多少网络安全技能?
现在可以看到很多标题都声称三个月内就可以转行网络安全领域,并且成为月入15K的网络工程师。那么,这个寒假的时间能学多少网络安全知识?是否能入门网络安全工程师呢? 答案是肯定的。 虽然网络完全知识是一门广泛的学科ÿ…...

六、肺癌检测-训练指标和数据增强
上一篇文章讲了训练过程和tensorboard可视化,这一篇文章记录下训练指标和数据增强的东西。 五、肺癌检测-数据集训练 training.py model.py_wxyczhyza的博客-CSDN博客 一、目标 1. 记录精度、召回率、F1分数 2. 样本均衡和样本随机化 3. 数据增强 二、要点 1…...

儿童饰品发夹发卡出口美国办理什么认证?
亚马逊美国站上传新产品,很多时候都是需要类目审核的,后台给出要求提供认证,产品类目不同,所需要提供的认证证书是不一样,儿童产品需要提交的是CPC认证,玩具,母婴用品,儿童书包&…...

Hive---Hive语法(一)
Hive语法(一) 文章目录Hive语法(一)Hive数据类型基本数据类型(与SQL类似)集合数据类型Hive数据结构数据库操作创建库使用库删除库表操作创建表指定分隔符默认分隔符(可省略 row formatÿ…...

微信小程序日记、微信小程序个人空间、个人日记
一.简述 个人比较喜欢微信小程序,因为小程序所追求的用户体验、代码质量、美观的样式,简单方便丰富的api、样式封装等,同时又与普通的前端开发非常相似,让人很容易就上手。 这篇博客介绍的是一款记录个人/家庭日常记录的微信小程…...
CentOS 8利用Apache安装部署下载服务器
1:部署的目的是做一个类似下面开源镜像网站,把一些软件或者资料上传到服务器上面,减少用户在互联网上下载资料,提高效率,减少病毒。 2:使用下面的命令配置本机的IP地址主机名等信息。后期使用IP地址进行访问…...

【数据结构与算法】顺序表增删查改的实现(动态版本+文件操作)附源码
目录 一.前言 二.顺序表 1.概念及结构 2.顺序表结构体的定义 3.初始化顺序表,销毁顺序表和打印 3.接口 a.尾插 SepListpushback 头插 SepListpushfront b.尾删 SepListpopback 头删 SepListpopfront c.查询 SepListsearch d.修改 SepListmodify 三…...
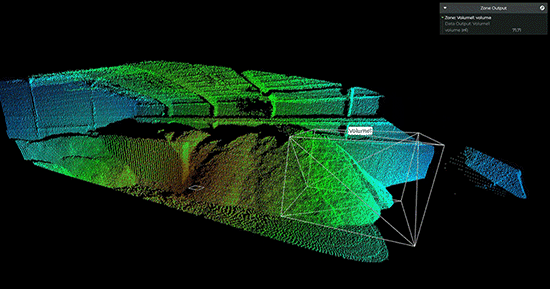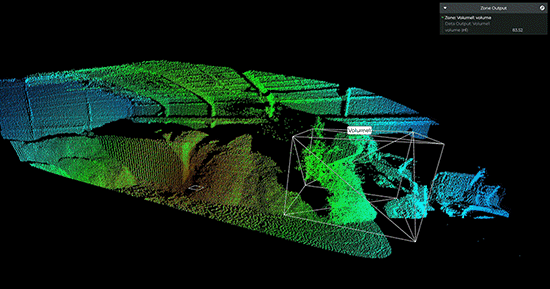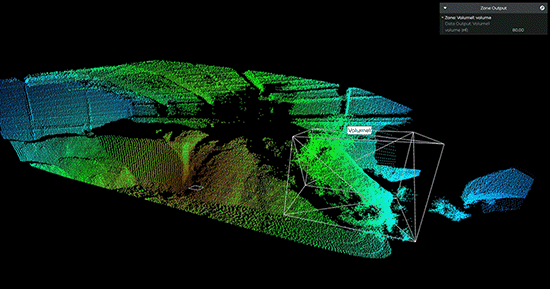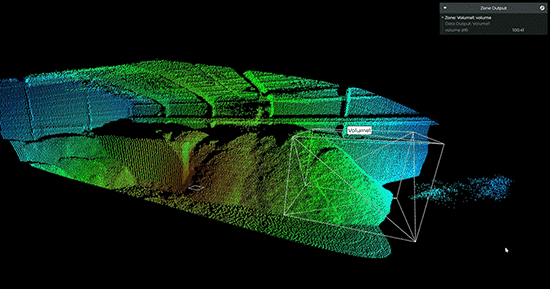
【虹科】基于Lidar的体积监控实现高效的库存管理
迄今为止,很多物料厂家测量库存的结果数据仍然不准确,会存在很大的误差,导致供应链效率低下——这个问题可以通过Lidar技术轻松解决。近年来,全球供应链的脆弱性已经多次得到证明。无论是油轮被困在苏伊士运河,阻塞海峡…...

一口吃不成ChatGPT,复旦版MOSS服务器被挤崩后续
ChatGPT 是目前最先进的 AI,由于 ChatGPT 的训练过程所需算力资源大、标注成本高,此前国内暂未出现对大众开放的同类产品。 适逢ChatGPT概念正火,2 月 21 日,复旦团队发布首个中国版类 ChatGPT 模型「MOSS」,没想到瞬时…...
html初识
HTML认知 文章目录HTML认知语法规范注释标签组成和关系标签的关系标签学习排版系列标签**标题标签****段落标签**换行标签水平线标签文本格式化标签媒体标签图片标签src 目标图片的路径alt 替换文本title 图片的标题width 宽度 / height 高度路径绝对路径相对路径(常…...
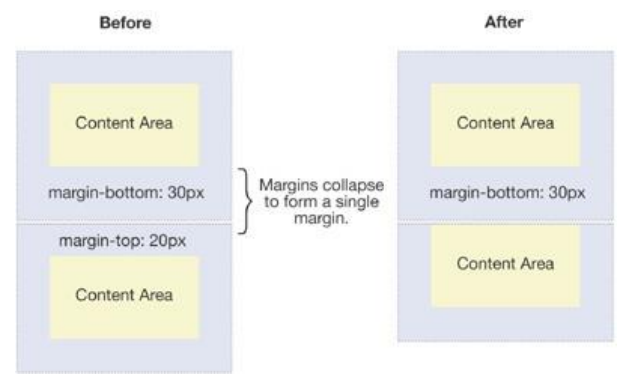
BFC的概念与作用
本篇详细介绍FC的概念,以及BFC的作用:FC的全称是Formatting Context,元素在标准流里面都是属于一个FC的.块级元素的布局属于Block Formatting Context(BFC) -也就是block level box都是在BFC中布局的; 行内…...

谷歌留痕代发技术指南_谷歌留痕怎么霸屏的?
本文主要分享谷歌留痕技术的一些常见问题,霸屏的原理是什么。 本文由光算创作,有可能会被修改和剽窃,我们佛系对待这种行为吧。 谷歌留痕也叫谷歌搜索留痕,那么谷歌搜索留痕的霸屏原理是什么? 答案是:利…...
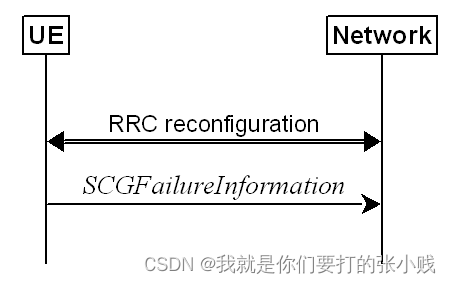
SCG failure information
我们知道5G网络有独立组网和非独立组网,独立组网中不论是核心网还是接入网都是5G,但是部署成本高;非独立组网也就是双连接(MRDC)也是目前比较流行的一种方式,其中的ENDC,即E-UTRA-NRDual Connectivity,是将…...
Idea修改Git账号及密码的方法
IDEA修改git账号及密码的方法:1、file->settings->passwords2、重启IDEA3、执行一次提交或更新当执行提交或更新之后,idea会自动提示输入账号、密码,如下:4、以上如果还修改不了,请尝试如下方式解决办法…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
