一起学数据结构(8)——二叉树中堆的代码实现
在上篇文章中提到,提到了二叉树中一种特殊的结构——完全二叉树。对于完全二叉树,在存储时,适合使用顺序存储。对于非完全二叉树,适合用链式存储。本文将给出完全二叉树的顺序结构以及相关的代码实现:
1. 二叉树的结构建立、销毁及初始化:
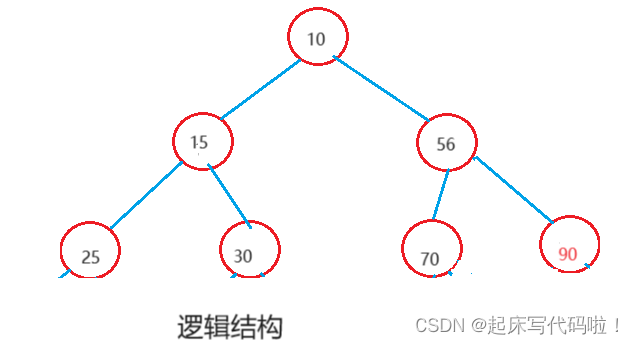
给出下图中二叉树的逻辑结构及存储结构:

二叉树的逻辑结构只是根据想象创建出来的结构,但是在计算机存储时,并不存在逻辑结构这种形式。而是下方的存储结构。所以,以下所有操作的对象都是存储结构中连续的数组。例如需要在上述二叉树中插入一个新的结点,并且此结点存储了元素。逻辑结构表示如下:
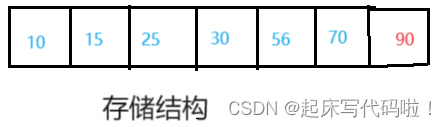
对于存储结构而言,以上操作只是在已有数组的末尾插入了一个值。存储结构表示如下:
所以,对于二叉树的结构建立,可以仿照之前的顺序表的结构,代码如下:
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;其中,指针用来后续进行连续空间的开辟,
表示数组的长度,
用来记录数据的容量,一旦
就需要进行扩容。
对于二叉树的销毁与初始化,与前面的文章中方式相同,只给出代码,不做多余解释:
二叉树的初始化如下:
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}二叉树的销毁如下:
void HeapDestory(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0;
}2.  向二叉树中插入结点:
向二叉树中插入结点:
2.1 HeapPush 向二叉树中插入结点:
前面提到,二叉树的逻辑结构在计算机中并不存在,并且下面的代码操作都是针对二叉树的逻辑结构的。所以,向二叉树中插入元素这一操作,实际就是在数组的末尾插入一个元素。但是在插入元素之前,需要判定数组的空间是否有剩余,即满足:。一旦
,则需要进行一次扩容。对于扩容这一步骤在之前的文章中多次使用,这里依旧直接给出代码:
void HeapPush(HP* php, HPDataType* x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* newnode = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (newnode == NULL){perror("realloc");exit(-1);}php->a = newnode;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;}2.2 针对二叉树为小堆情况下,新插入元素的位置调整:
2.2.1 结点调节的逻辑分析:
例如对于上面给出的完全二叉树,可以看出,这个二叉树满足父结点数值子结点数值,为小堆
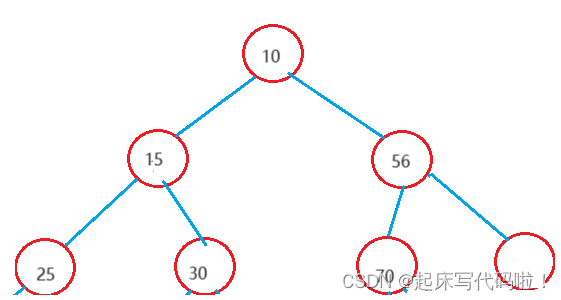
对于新结点中插入的数值,需要区分下列情况进行判定:
1. 插入的值大于父结点中的数值,即:
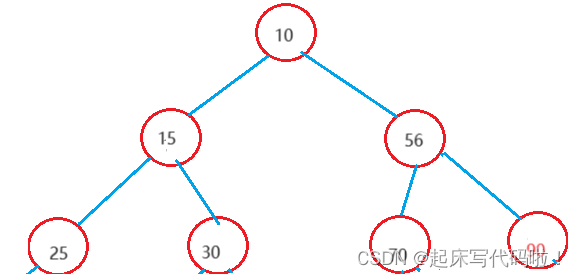
此时插入的结点的数值为,依旧满足子结点数值
父结点数值,因此不需要对结点的关系进行更改。
2. 插入的值小于父结点中的数值:
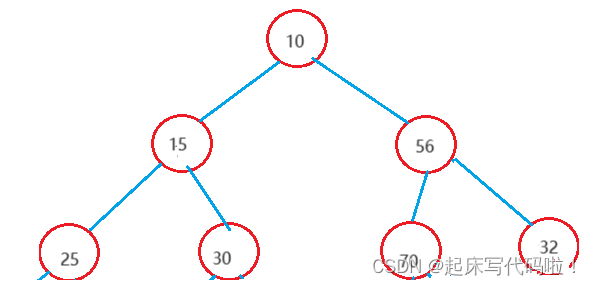
此时插入的结点中存储的值为。不满足小堆中父结点存储的值
子结点的关系。所以,需要对二叉树的关系进行更改,即对此时的子结点、父结点交换位置,效果如下:

但是,如果插入的结点中存储的值,小于二叉树中任何结点的值,例如新插入结点中存储的值为。此时调整后的二叉树的效果如下:
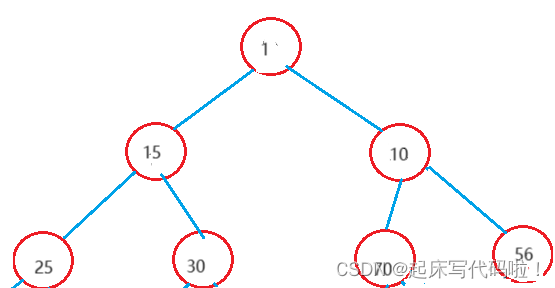
对于调整父结点、子结点的关系,在上一篇文章中,根据完全二叉树的性质给出了下列的等式:
对于一个父结点,假设其在数组中的下标为,则其左子结点的下标:
其右子结点的下标为:
对于任意子结点(左、右子结点都适用),其父结点的下标可以用下面的等式表示,及:
定义函数用于完成对子结点、父结点关系的调整:
前面提到,对于插入子结点,最极端的情况就是子结点中存储的值小于二叉树中任意结点的值,导致子结点需要一直与父结点进行替换,直至到根结点,即数组中下标为的结点的位置。因此需要利用循环来控制结点的调整次数,通过上面的分析可以得出,循环的条件就是子结点对应的下标
,即:
。
2.2.2 Adjustup 结点调节的代码分析:
对于上面的给出的向二叉树中插入元素的操作中,需要注意,在插入元素后,会对表示数组长度的,所以,每次进行上述插入操作后:
-数组的实际长度
。
上面说到,会创建函数函数来调整结点的位置,整个操作中,需要知道子结点、父结点的下标,因为父结点的下标可以通过上面给出的等式进行计算。所以,在对函数传递参数时,只需要传递数组的指针和插入的子结点的下标。因为插入的结点为数组的最后一位,所以,直接传递数组的实际长度,即
即可。
对于交换子结点和父节点这一功能在后面需要多次适用,所以,为了方便,直接再创建一个交换函数即可。交换函数对应的代码如下:
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType* tmp = *p1;*p1 = *p2;*p2 = tmp;
}调整函数代码如下:
void Adjustup(HPDataType* a, int child)
{assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}对于上面已经给出的插入函数,在最后加上已经定义好的调整函数即可。
为了验证前面的功能是否正常,再定义函数用于打印二叉树的结点。打印函数嗲澳门如下:
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}
}通过下面的代码,对插入并且调整结点的函数进行验证:
#include"TreeNode.h"void Test1()
{int a[] = { 9,8,7,5,4,3,2 };HP hp;HeapInit(&hp);for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}HeapPrint(&hp);HeapDestory(&hp);}
int main()
{Test1();return 0;
}运行结果如下:
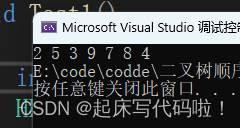
运行结果显示的是二叉树的存储结构,将上述存储结构转为逻辑结构,即:
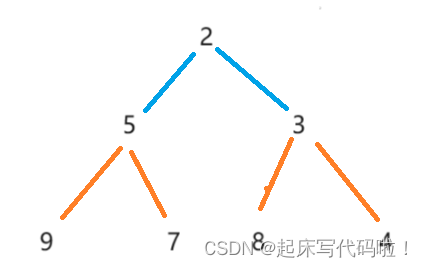
满足小堆的定义。
3.删除二叉树中的结点:
3.1 删除二叉树中结点逻辑分析:
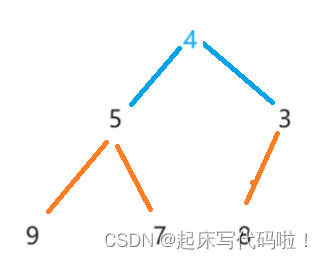
给定下列的二叉树:
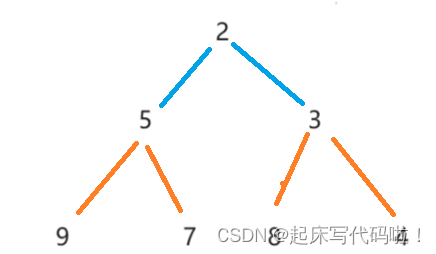
对于二叉树的删除结点而言,删除尾部结点的意义并不大,所以,一般的删除结点都是指删除二叉树的根结点。
前面提到,对于二叉树的操作,是作用在二叉树的存储结构上,上图二叉树的存储结构如下:
对于一个连续的数组,删除头结点的方式可以是让后面的元素依次向前覆盖。但是对于二叉树而言,向前覆盖来删除头结点的方式可能会造成二叉树的结构错误,例如,利用覆盖的方法删除了头结点的二叉树的逻辑结构如下:
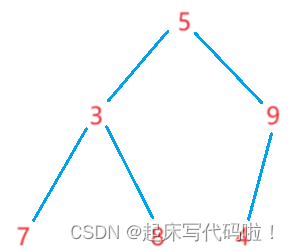
调整过后的二叉树,将不再满足上方的小堆关系,即子结点存储的数据父结点存储的数据。并且,再顺序表的文章中就提到,对于依次覆盖这种方法,时间复杂度为
,效率并不高。
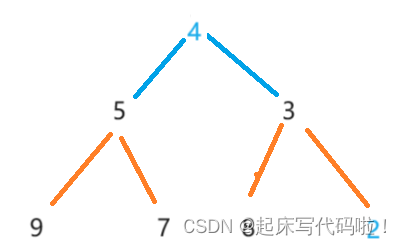
为了解决上面的问题,给定下方的方法来完成对于根结点的删除:
首先,将二叉树的尾结点和根结点替换,效果如下:
对于二叉树的存储结构,可以随机访问数组的任意下标所对应的位置,并且尾插和尾删的效率为,所以,直接将尾结点删除,即:
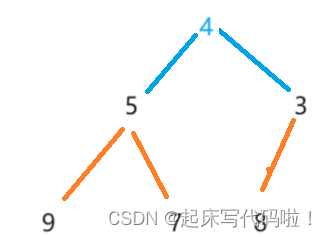
通过上述方法删除了二叉树的原根结点之后,此时二叉树的子树并没有受到影响,依旧是小堆,删除了二叉树的原根结点后,需要对二叉树中的结点的位置进行调整。
在调整位置时,需要先比较结点的子结点所存储的数据的大小,例如根节点的子结点分别存储了数据,由于根节点存储的数据
大于右子结点所存储的数据
,因此两个结点交换位置。
需要注意,此处的调整并不同于上方给出的调整函数。上方的函数调整的对象是针对于新插入的尾结点。调整的方向是总体向上的,本处的调整是针对于置换完后的新的根结点,总体的方向是自上而下的,因此,此处再构建另一个调整函数
。
3.2 代码分析——Adjustdown 删除二叉树中结点:
对于调整函数,首先判断非叶子结点的子结点的大小关系,并找到较小的一个。可以先假设一个结点为小结点(此处默认左子结点为小结点),对于左子结点的下标,可以通过上面的等式
得出,对于右子结点,可以表示为 ,再对两个结点中数据的大小进行判定,如果
,则表示右子结点为较小的结点,让
,反之不变。此处需要注意一种特殊情况,及:
此时,存储数据的结点只有左结点,没有右结点,
会引起数组的越界访问,所以,在进行结点大小判定之前,需要判定
。
找到左、右子结点中较小的一个后,对父结点 、子结点的大小进行判定,如果子结点中存储的数据小于父结点中的数据,则交换两个结点的位置。
对于交换这一过程,最好的情况下是交换一次,最坏的情况下是交换到叶子结点。所以,判断循环是否进行的条件便是判断的大小是否
。对应代码如下:
void Adjustdown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;while ( child < size){if (child+1 < size && a[child + 1] < a[child]){child++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}3.3 代码分析——HeapPop 删除二叉树中的结点:
删除结点一共需要下列步骤:
1. 交换首位结点
2. 删除尾结点
3.通过调整函数对结点的位置进行调整
对应代码如下:
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;Adjustdown(php->a, php->size, 0);}4. 返回根结点所存储的数据:
原理较为简单,只给出代码,不做解释:
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}5. 探空:
原理较为简单,只给出代码,不做解释:
bool Heapbool(HP* php)
{assert(php);return php->size == 0;
}
6. 代码总览:
头文件如下:
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;void HeapInit(HP* php);void HeapDestory(HP* php);void HeapPush(HP* php, HPDataType* x);void Adjustup(HPDataType* a, int child);void Swap(HPDataType* p1, HPDataType* p2);void HeapPrint(HP* php);void Adjustdown(HPDataType* a, int size, int parent);void HeapPop(HP* php);HPDataType HeapTop(HP* php);bool HeapEmpty(HP* php);TreeNode.c文件如下:
#include"TreeNode.h"void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = 0;php->capacity = 0;
}void HeapDestory(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = 0;php->capacity = 0;
}
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType* tmp = *p1;*p1 = *p2;*p2 = tmp;
}//新插入子结点向上升,
void Adjustup(HPDataType* a, int child)
{assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void HeapPush(HP* php, HPDataType* x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* newnode = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (newnode == NULL){perror("realloc");exit(-1);}php->a = newnode;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;Adjustup(php->a, php->size-1);
}
//健小堆
void Adjustdown(HPDataType* a, int size, int parent)
{int child = parent * 2 + 1;while ( child < size){//找出较小的结点if (child+1 < size && a[child + 1] > a[child]){child++;}if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;Adjustdown(php->a, php->size, 0);}HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}Test.c文件:
int main()
{Test1();int a[] = { 70,65,100,32,50,60 };HPqort(a, sizeof(a) / sizeof(int));printf("\n");for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}return 0;
}相关文章:
一起学数据结构(8)——二叉树中堆的代码实现
在上篇文章中提到,提到了二叉树中一种特殊的结构——完全二叉树。对于完全二叉树,在存储时,适合使用顺序存储。对于非完全二叉树,适合用链式存储。本文将给出完全二叉树的顺序结构以及相关的代码实现: 1. 二叉树的结构…...
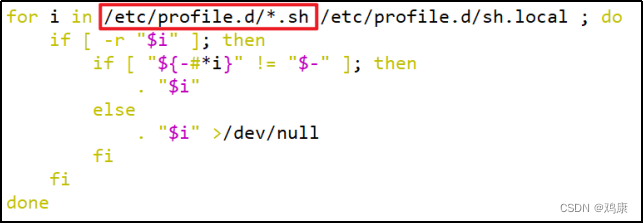
Linux环境变量配置说明(配置jdk为例-摘录自尚硅谷技术文档)
配置环境变量的不同方法 Linux的环境变量可在多个文件中配置,如/etc/profile,/etc/profile.d/.sh,~/.bashrc,~/.bash_profile等,下面说明上述几个文件之间的关系和区别。 bash的运行模式可分为login shell和non-login shell。 例…...

idea常用插件笔记
文章目录 Free Mybatis Toollombok插件idea插件导出导入 idea提供了很多好用的插件,之前都装了的,但是换了下电脑,什么都没了,所以记录下方便以后用。 Free Mybatis Tool mybatis跳转插件,再也不用费力的找xml了。 l…...
搜索二叉树【C++】
文章目录 二叉搜索树二叉搜索树的模拟实现构造函数拷贝构造函数赋值运算符重载函数析构函数Insert循环递归 Erase循环递归 Find循环递归 二叉搜索树的应用K模型KV模型 完整代码普通版本递归版本 二叉搜索树 二叉搜索树又称为二叉排序树,它或者是一棵空树࿰…...
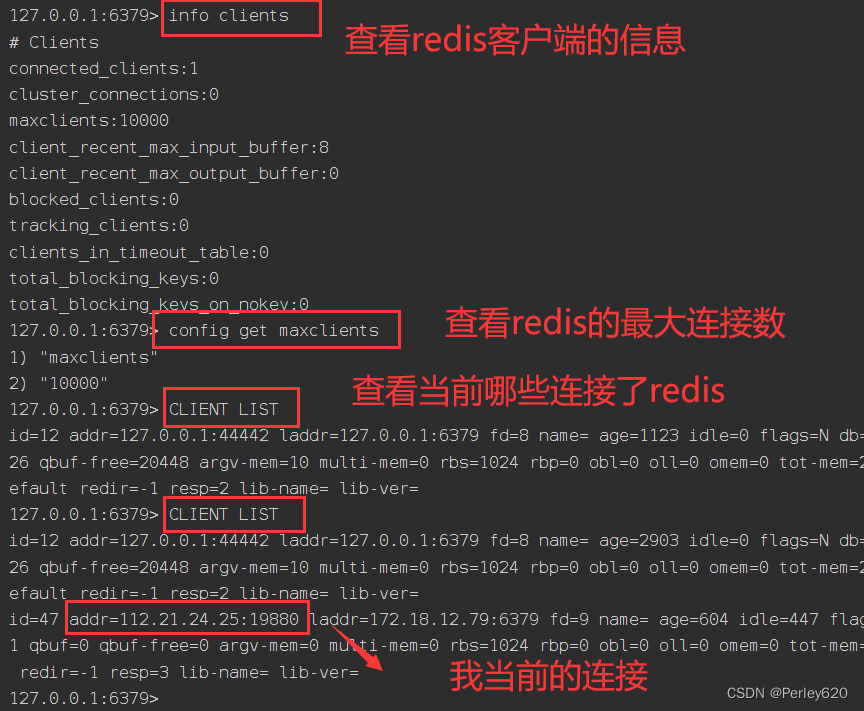
华为云云耀云服务器L实例评测|认识redis未授权访问漏洞 漏洞的部分复现 设置连接密码 redis其他命令学习
前言 最近华为云云耀云服务器L实例上新,也搞了一台来玩,期间遇到过MySQL数据库被攻击的情况,数据丢失,还好我有几份备份,没有造成太大的损失。昨天收到华为云的邮箱提醒,我的redis数据库没有设置密码&…...

快速安装NGINX
快速安装NGINX #安装依赖包 yum -y install gcc pcre pcre-devel zlib zlib-devel openssl openssl-devel#下载NGINX curl -O https://nginx.org/download/nginx-1.21.6.tar.gz#解压NGINX tar -zxvf nginx-1.21.6.tar.gz cd nginx-1.21.6.tar.gz#配置 ./configure --prefix/…...
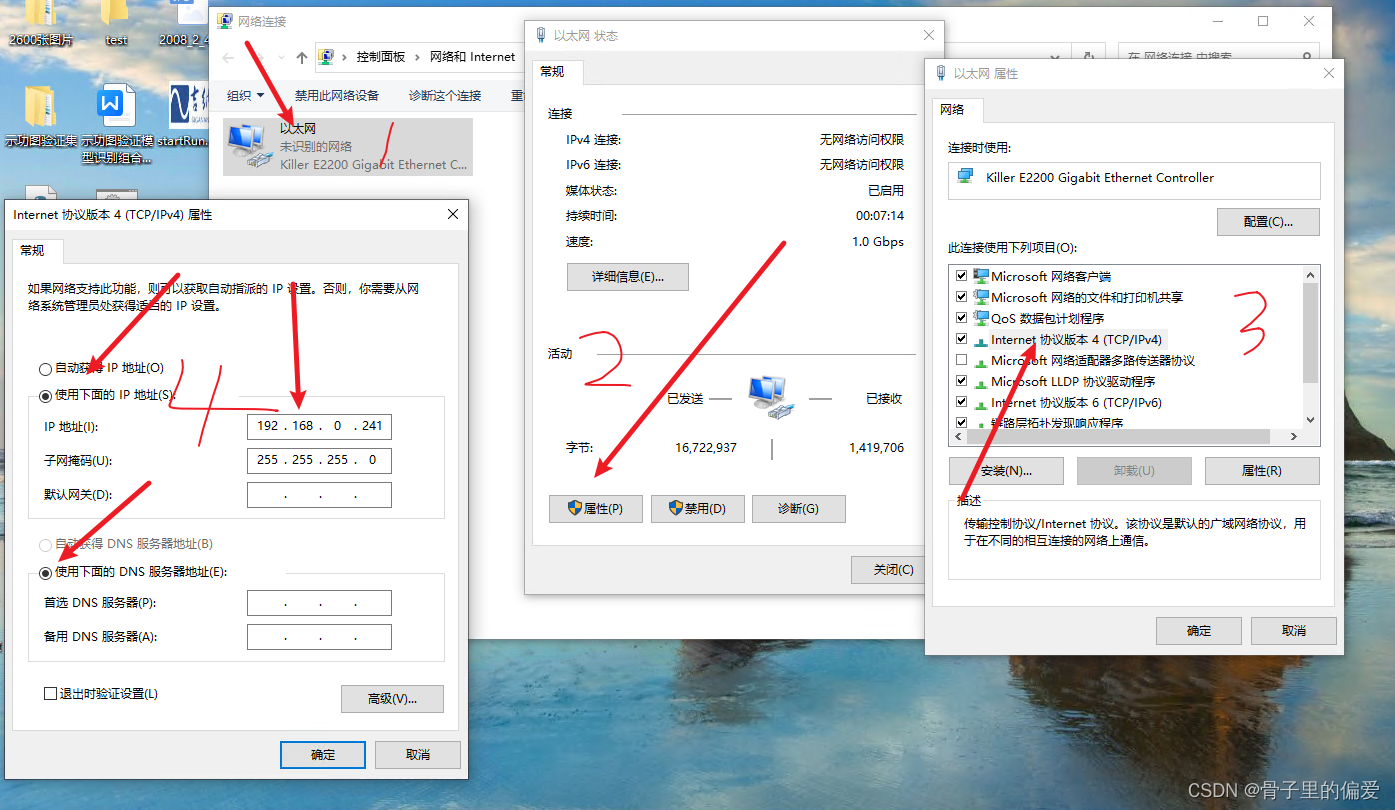
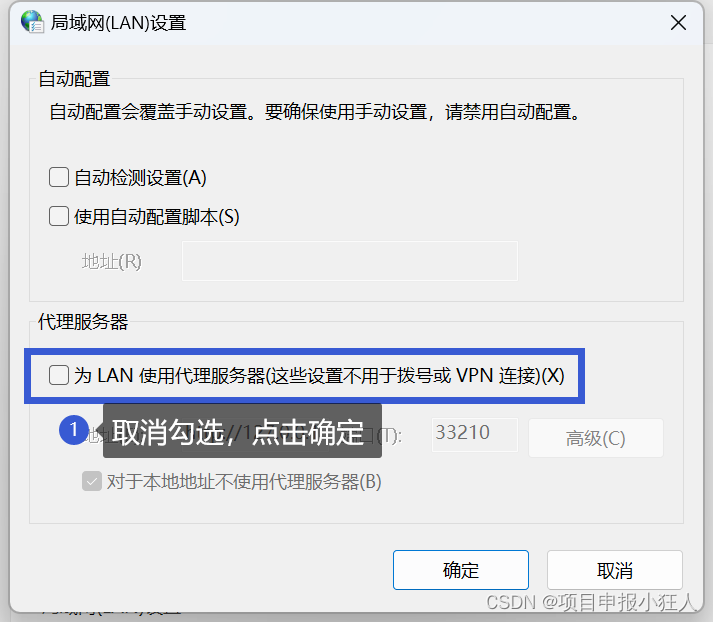
一台电脑远程内网的另外一台电脑,禁止远程的电脑连接外网,只允许内网连接
一台电脑远程内网的另外一台电脑,禁止远程的电脑连接外网,只允许内网连接 1.找到右下角网卡图标,右键图标选择“打开网络和共享中心”。 3、点击“更改适配器设置”。 4、右键正在使用的网卡“本地连接”打开属性 5、找到“internet协…...

山西电力市场日前价格预测【2023-09-24】
日前价格预测 预测说明: 如上图所示,预测明日(2023-09-24)山西电力市场全天平均日前电价为496.09元/MWh。其中,最高日前电价为705.54元/MWh,预计出现在14: 30。最低日前电价为333.70元/MWh,预计…...

MQ---第二篇
系列文章目录 文章目录 系列文章目录一、RabbitMQ事务消息二、RabbitMQ死信队列、延时队列一、RabbitMQ事务消息 通过对信道的设置实现 channel.txSelect();通知服务器开启事务模式;服务端会返回Tx.Select-Okchannel.basicPublish;发送消息,可以是多条,可以是消费消息提交…...

C++ 创建文件并写入内容
文章目录 1.问题2.filesystem3.示例参考文献 1.问题 C 如何向指定路径的文件写入内容呢? 这里有几点要求: 如果目录不存在需要自动创建。如果文件不存在需要自动创建。以覆盖的方式写入内容。 2.filesystem C17 带来了一个新的库:filesy…...

微信小程序rich-text里面写多行溢出显示省略号在ios中不显示的问题
问题:微信小程序rich-text里面写多行溢出显示省略号在ios中不显示的问题 解决方法:需要给一个默认的div标签,在div写行内样式 overflow : hidden; text-overflow: ellipsis; display: -webkit-box; -webkit-line-clamp: 3; -webkit-box-o…...
解决Win11/10中Edge浏览器页面加载不出来、打不开问题|有网但是打不开,加载不了
问题症状 edge浏览器打不开,有网络能正常上网,但是edge浏览器无法浏览。网络质量很高,但是页面就是加载不出来,详情如下: (我是在科学上网后造成这样子的原因,现在将我的方法分享一下ÿ…...

【DRAM存储器五】DRAM存储器的架构演进-part2
👉个人主页:highman110 👉作者简介:一名硬件工程师,持续学习,不断记录,保持思考,输出干货内容 参考书籍:《Memory Systems - Cache, DRAM, Disk》 目录 以提升吞吐…...
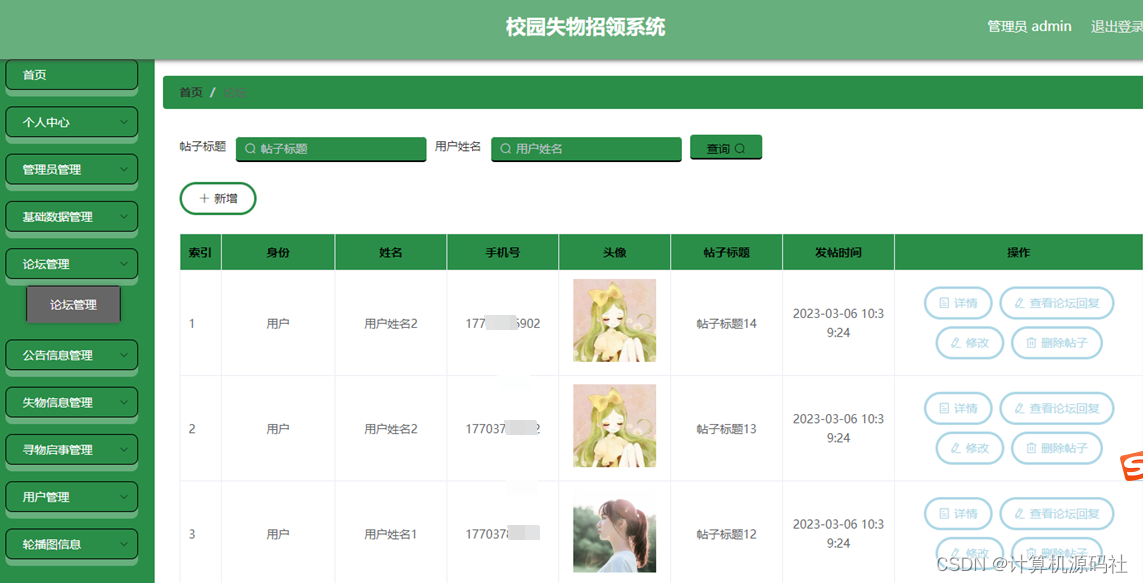
分享一个基于uniapp+springboot技术开发的校园失物招领小程序(源码、lw、调试)
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! 💕&…...
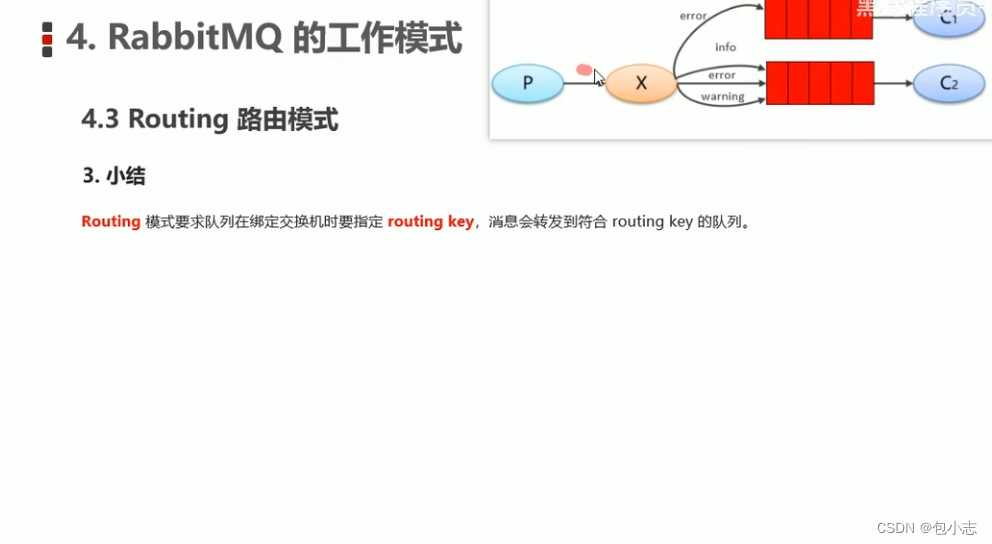
RabbitMQ工作模式——Routing路由模式
1.Routing路由模式 Routing生产者代码 public class Producer_Routing {public static void main(String[] args) throws IOException, TimeoutException {//1.创建连接工厂ConnectionFactory factory new ConnectionFactory();//2.设置参数factory.setHost("172.16.98.…...

Python字典的增删改查以及嵌套
嗨喽,大家好呀~这里是爱看美女的茜茜呐 👇 👇 👇 更多精彩机密、教程,尽在下方,赶紧点击了解吧~ python源码、视频教程、插件安装教程、资料我都准备好了,直接在文末名片自取就可 字典 基础数…...

【淘宝开店】新手入门开网店教程
一、上架产品流程顺序 1. 上架10个产品2. 早中晚各上架1件产品3. 连续上架4天 二、产品培训 动销率要求: 店铺产品数必须>10公式: 店铺最近30天有销量产品数 / 店铺上架总产品数 * 100%1. 从动销率可以得出, 店铺产品不宜过多2. 小卖家前期最佳建议产品数10个 三、上架产品…...
(五)(TCP拥塞控制))
计网第五章(运输层)(五)(TCP拥塞控制)
目录 一、基本概念 二、拥塞控制算法 慢开始: 拥塞避免: 快重传: 快恢复: 一、基本概念 若对网络中某一资源的需求超过了该资源所能提供的可用部分(供不应求),网络性能就会变坏。 在计算…...
windows/ubuntu怎么修改hosts文件
windows系统修改方法: 第一步:用管理员权限打开记事本,或者visual studio。 第二步:用记事本或者vs打开地址C:\Windows\System32\drivers\etc\hosts文件,这个时候就可以直接修改了 Ubuntu22 LTS系统修改方法…...
大数据基础知识点1-关系型数据库)
(日积月累版)大数据基础知识点1-关系型数据库
好久不见,甚是想念。 笔者最近有时间整理关于大数据的一些基础知识点,整理的目不在于能提升多少技能,关键在于巩固一些很基础的知识点,毕竟互联网就是基础略稳固的人比较有优势,在遇到或发现一些技术问题时,…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...
