组队竞赛（int溢出问题）

目录

一、题目

二、代码

（一）没有注意int溢出

（二）正确代码

1. long long sum=0

2. #define int long long

3. 使用现成的sort函数

---

一、题目

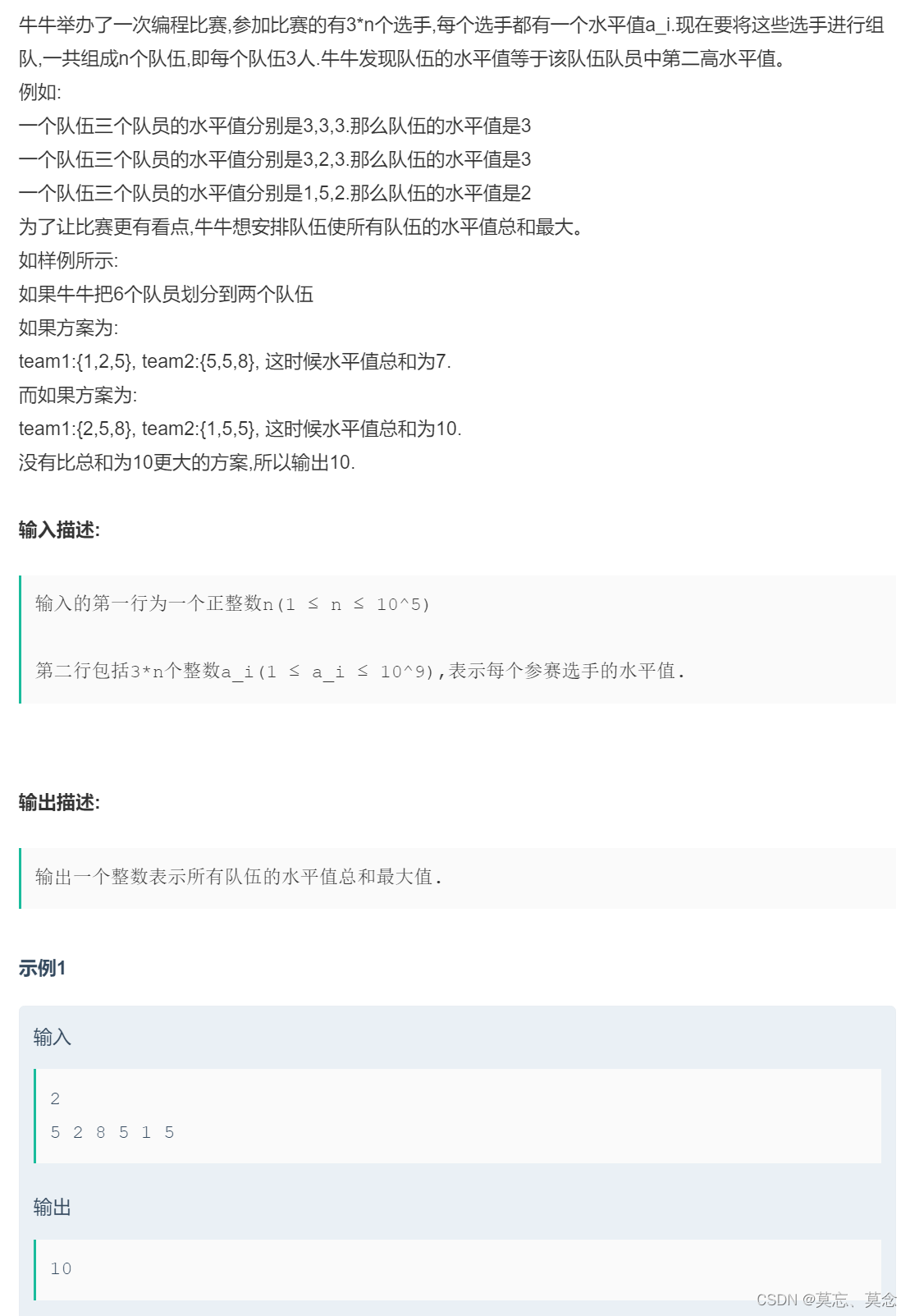
二、代码

（一）没有注意int溢出

 

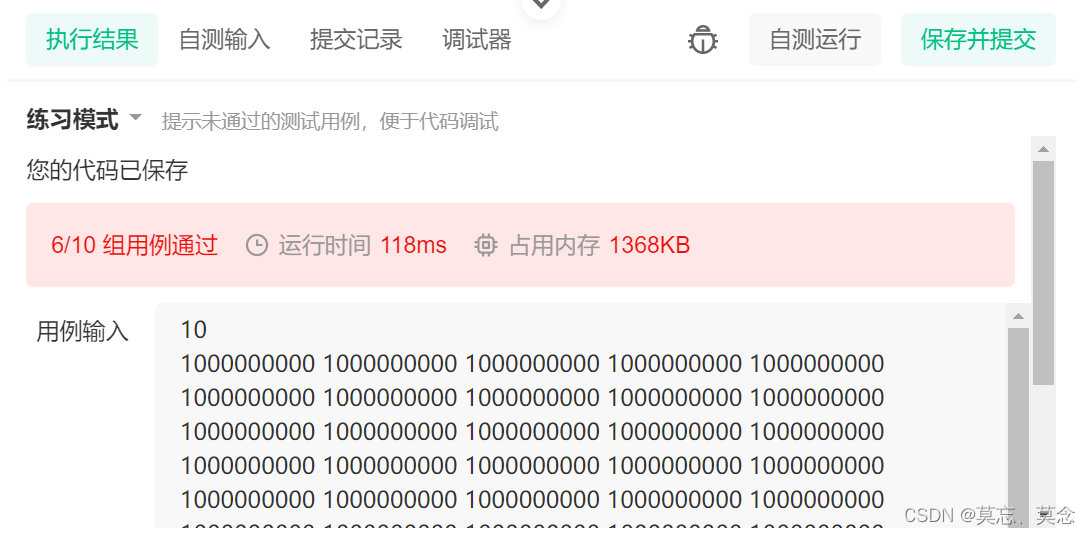
#include <iostream>
#include<algorithm>
#include <vector>
using namespace std;
void QuickSort(vector<int>&a,int begin,int end)//快排
{if(begin>=end)return;int left = begin;int right = end;int keyi = left;//基准值的下标while(left<right)//降序排列{while(left<right && a[right]>=a[keyi]){--right;}while(left<right && a[left]<=a[keyi]){++left;}swap(a[left],a[right]);}swap(a[left],a[keyi]);QuickSort(a,begin,left);QuickSort(a,left+1,end);
}
int main() 
{int n;cin>>n;vector<int>data(3*n,0);for(int i=0;i<3*n;i++){cin>>data[i];}QuickSort(data,0,3*n-1);int k=1;int sum=0;for(int i=3*n-2;i>=0&& k<=n;i-=2){sum+=data[i];k++;}cout<<sum;return 0;
}

（二）正确代码

1. long long sum=0

#include <iostream>
#include<algorithm>
#include <vector>
using namespace std;
void QuickSort(vector<int>&a,int begin,int end)//快排
{if(begin>=end)return;int left = begin;int right = end;int keyi = left;//基准值的下标while(left<right)//升序排列{while(left<right && a[right]>=a[keyi])//右边找小{--right;}while(left<right && a[left]<=a[keyi])//左边找大{++left;}swap(a[left],a[right]);}swap(a[left],a[keyi]);QuickSort(a,begin,left);QuickSort(a,left+1,end);
}
int main() 
{int n;cin>>n;vector<int>data(3*n,0);for(int i=0;i<3*n;i++){cin>>data[i];}QuickSort(data,0,3*n-1);int k=1;long long sum=0;for(int i=3*n-2;i>=0&& k<=n;i-=2){sum+=data[i];k++;}cout<<sum;return 0;
}

2. #define int long long

#include <iostream>
#include<algorithm>
#include <vector>
using namespace std;#define int long long
void QuickSort(vector<int>&a,int begin,int end)//快排
{if(begin>=end)return;int left = begin;int right = end;int keyi = left;//基准值的下标while(left<right)//升序排列{while(left<right && a[right]>=a[keyi])//右边找小{--right;}while(left<right && a[left]<=a[keyi])//左边找大{++left;}swap(a[left],a[right]);}swap(a[left],a[keyi]);QuickSort(a,begin,left);QuickSort(a,left+1,end);
}
signed main() 
{int n;cin>>n;vector<int>data(3*n,0);for(int i=0;i<3*n;i++){cin>>data[i];}QuickSort(data,0,3*n-1);int k=1;int sum=0;for(int i=3*n-2;i>=0&& k<=n;i-=2){sum+=data[i];k++;}cout<<sum;
}

3. 使用现成的sort函数

#include <iostream>
#include<algorithm>
#include <vector>
using namespace std;
int main() 
{int n;cin>>n;vector<int>data(3*n,0);for(int i=0;i<3*n;i++){cin>>data[i];}sort(data.begin(),data.end());//默认升序排列int k=1;long long sum=0;for(int i=3*n-2;i>=0&& k<=n;i-=2){sum+=data[i];k++;}cout<<sum;return 0;
}