动态系统的建模与分析
前言
CS小菜鸡控制理论入门
视频学习笔记
视频传送门:动态系统的建模与分析】9_一阶系统的频率响应_低通滤波器_Matlab/Simulink分析
拉普拉斯变换
F(s)=L{f(t)}=∫0∞f(t)e−stdtF(s)=\mathcal{L}\{f(t)\}=\int_0^\infty f(t)e^{-st}\mathrm{d}tF(s)=L{f(t)}=∫0∞f(t)e−stdt,其中s=σ+jωs=\sigma+j\omegas=σ+jω
L{f′(t)}=sF(s)−f(0)\mathcal{L}\{f'(t)\}=sF(s)-f(0)L{f′(t)}=sF(s)−f(0)
L{f′′(t)}=s2F(s)−sf(0)−f′(0)\mathcal{L}\{f''(t)\}=s^2F(s)-sf(0)-f'(0)L{f′′(t)}=s2F(s)−sf(0)−f′(0)
L{∫0tf(τ)d(τ)}=1sF(s)\mathcal{L}\{\int_0^t f(\tau)d(\tau)\}=\frac{1}{s}F(s)L{∫0tf(τ)d(τ)}=s1F(s)
一个电路例子:
e′=Li′′+Ri′+1cie'=Li''+Ri'+\frac{1}{c}ie′=Li′′+Ri′+c1i
sE(s)=Ls2I(s)+RsI(s)+1cI(s)sE(s)=Ls^2I(s)+RsI(s)+\frac{1}{c}I(s)sE(s)=Ls2I(s)+RsI(s)+c1I(s)
sE(s)=(Ls2+Rs+1c)I(s)sE(s)=(Ls^2+Rs+\frac{1}{c})I(s)sE(s)=(Ls2+Rs+c1)I(s)
I(s)=sLs2+Rs+1cE(s)I(s)=\frac{s}{Ls^2+Rs+\frac{1}{c}}E(s)I(s)=Ls2+Rs+c1sE(s)
常系数微分方程⟺\iff⟺线性时不变系统
非线性化系统:1.在平衡点处线性化 2.采用非线性化分析控制
拉普拉斯变换求解线性微分方程:
- 运用L\mathcal{L}L将ttt域转化到sss域;
- +−×÷+-\times \div+−×÷;
- 运用L−1\mathcal{L^{-1}}L−1将sss域转化到ttt域;
拉普拉斯逆变换
F(s)=5−ss2+5s+4F(s)=\frac{5-s}{s^2+5s+4}F(s)=s2+5s+45−s
F(s)=−3s+4+2s+1F(s)=\frac{-3}{s+4}+\frac{2}{s+1}F(s)=s+4−3+s+12
L−1[F(s)]=−3e−4t+2e−t\mathcal{L^{-1}}[F(s)]=-3e^{-4t}+2e^{-t}L−1[F(s)]=−3e−4t+2e−t
s=−4,−1s=-4,-1s=−4,−1:传递函数(Transfer Function)的极点(Poles)
一阶系统的单位阶跃响应(Step Response)
x˙(t)+gRx(t)=u(t)\dot{x}(t)+\frac{g}{R}x(t)=u(t)x˙(t)+Rgx(t)=u(t)
x(t)=CRg(1−e−gRt)x(t)=\frac{CR}{g}(1-e^{-\frac{g}{R}t})x(t)=gCR(1−e−Rgt)
时间常数t=τt=\taut=τ,满足x(τ)=1−1e=0.63x(\tau)=1-\frac{1}{e}=0.63x(τ)=1−e1=0.63
稳定(整定)时间 Tss=4τTss=4\tauTss=4τ
用于系统辨识:
假设 Tss=4Tss=4Tss=4,则τ=1=Rg\tau=1=\frac{R}{g}τ=1=gR
CRg=5⟹C=5\frac{CR}{g}=5\Longrightarrow C=5gCR=5⟹C=5
u(s)⟶as+a⟶x(s)u(s) \longrightarrow \frac{a}{s+a} \longrightarrow x(s)u(s)⟶s+aa⟶x(s):本质上是一个低通滤波器
频率响应
input: Misin(ωt+ϕi)M_isin(\omega t+\phi_i)Misin(ωt+ϕi)
output: M0sin(ωt+ϕ0)M_0sin(\omega t+\phi_0)M0sin(ωt+ϕ0)振幅响应:M0Mi=M\frac{M_0}{M_i}=MMiM0=M
幅角响应:ϕ0−ϕi=ϕ\phi_0-\phi_i=\phiϕ0−ϕi=ϕ
(一番数学推导…)
conclusion
MG=∣G(jω)∣M_G=|G(j\omega)|MG=∣G(jω)∣
ϕG=∠G(jω)\phi_G=\angle G(j\omega)ϕG=∠G(jω)
相关文章:

动态系统的建模与分析
前言 CS小菜鸡控制理论入门 视频学习笔记 视频传送门:动态系统的建模与分析】9_一阶系统的频率响应_低通滤波器_Matlab/Simulink分析 拉普拉斯变换 F(s)L{f(t)}∫0∞f(t)e−stdtF(s)\mathcal{L}\{f(t)\}\int_0^\infty f(t)e^{-st}\mathrm{d}tF(s)L{f(t)}∫0∞f(t)…...

QCC51XX---HCI log
高通在新的S3/S5以及往后新的平台上面,引入了一个新的调试功能。就是标题说的HCI log,他类似air trace那样用来分析蓝牙协议的,这样我们就可以很详细地找到通信协议之间哪个部分出了问题。以前我们都是通过抓包器抓air trace分析的,抓包器一个要几十万,学会这个功能就相当…...
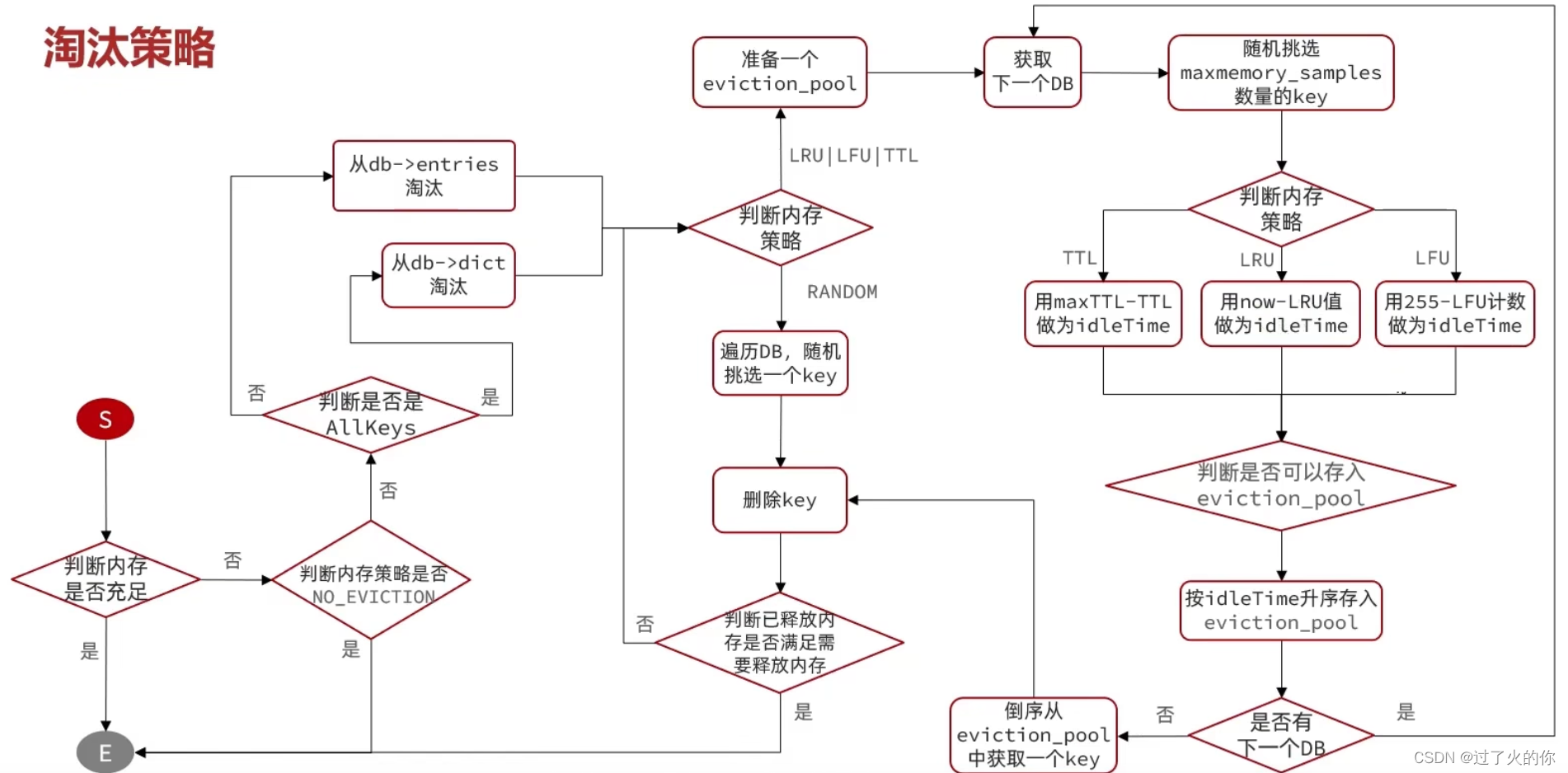
Redis四 原理篇
《Redis四 原理篇》 提示: 本材料只做个人学习参考,不作为系统的学习流程,请注意识别!!! 《Redis四 原理篇》《Redis四 原理篇》1、原理篇-Redis数据结构1.1 Redis数据结构-动态字符串1.2 Redis数据结构-intset1.3 Redis数据结构-Dict1.4 Redis数据结构-ZipList1.4.1 Redis数据…...

从0开始写Vue项目-Vue实现数据渲染和数据的增删改查
从0开始写Vue项目-环境和项目搭建_慕言要努力的博客-CSDN博客从0开始写Vue项目-Vue2集成Element-ui和后台主体框架搭建_慕言要努力的博客-CSDN博客从0开始写Vue项目-Vue页面主体布局和登录、注册页面_慕言要努力的博客-CSDN博客从0开始写Vue项目-SpringBoot整合Mybatis-plus实现…...

AI技术的发展,人工智能对我们的生活有那些影响?
人工智能(Artificial Intelligence),英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。 人工智能是计算机科学的一个分支,它企图了解智能的实质,并生产出一…...
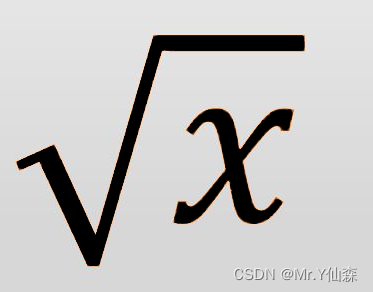
Unity中的Mathf数学运算讲解(值得收藏)
Unity中的Mathf数学运算有哪些? Mathf.Abs(f)绝对值 计算并返回指定参数 f 绝对值 例如: // 输出 10 Debug.log(Mathf.Abs(-10)) Debug.log(Mathf.Abs(10))Mathf.Sin正弦 static function Sin (f : float) : float 计算并返回以弧度为单位指定的角 f 的…...
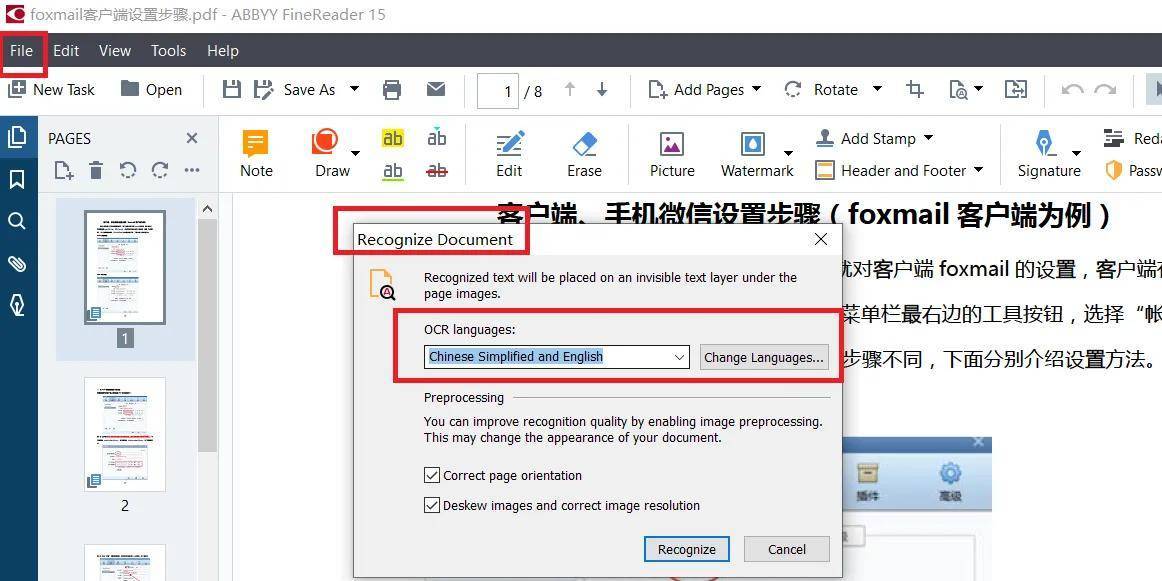
ABBYY FineReader16最新PDF图片文字识别软件
ABBYY FineReader16是非常好的一款 OCR 识别软件(可以识别不可编辑的PDF和图片文件),操作非常简单。ABBYY FineReader 16是一款知名的OCR文字识别软件(图片文字识别)。ABBYY 16采用了ABBYY最新推出的基于AI的OCR技术&a…...
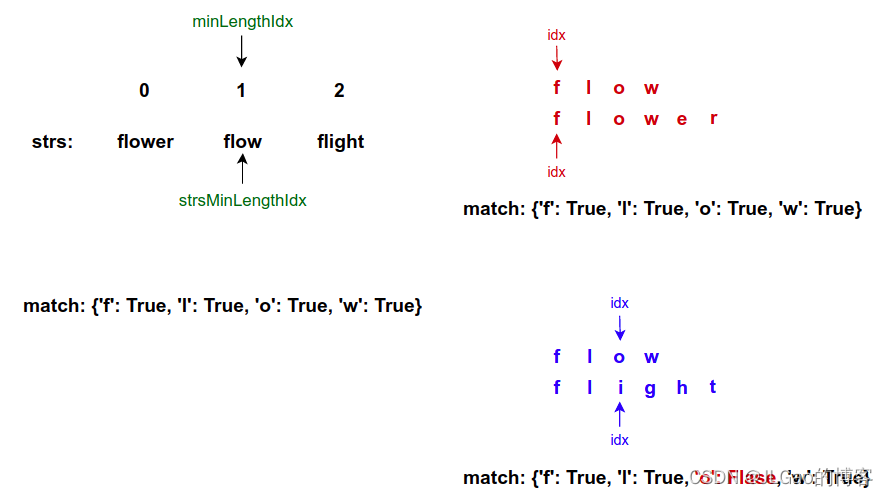
Leetcode14. 最长公共前缀
一、题目描述: 编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀,返回空字符串 “”。 示例 1: 输入:strs [“flower”,“flow”,“flight”] 输出:“fl” 示例 2: 输入:…...
JTT808jt1078
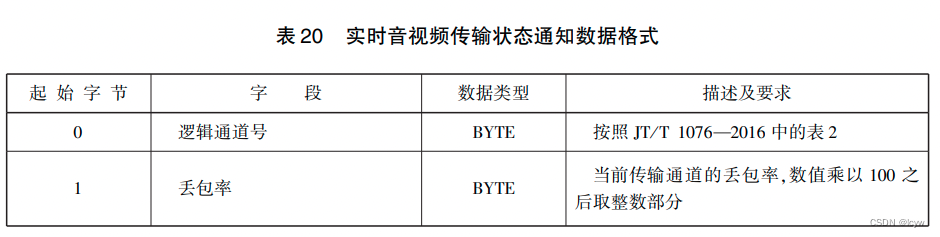
前言 交通部与2016年10月份推出了JT/T 1078-2016标准,全称是<道路运输车辆卫星定位系统视频通信协议> JTT808 808消息头内容如下表所示: 起始字节字段数据类型描述及要求0消息IDWORD2消息体属性WORD消息体属性格式结构图见图24终端手机号BCD[6…...

数字孪生加持,水利水电工程或将实现全生命周期管理
水利水电工程在数字孪生技术的加持,使得建设和运营更加高效和智能化,将工程中各种元素、过程和系统数字化,并建立数字孪生模型,以实现工程建设和运营的智能化管理。数字孪生对水利水电实现对工程建设的全生命周期管理,…...
RA4M2开发(3)----读取ISL29035数据,并在OLED上显示,串口打印
概述 HS3003是一种数字式温湿度传感器,可以测量环境中的温度和湿度。读取HS3003的数据需要连接传感器到一个数据采集系统,一般是微处理器或者单片机。以下是一个简单的读取HS3003数据的概述: 连接电路:将HS3003传感器连接到微处…...

密码复杂度
检查账户认证失败次数限制 修复建议: 配置SSH方式账户认证失败次数限制 编辑/etc/pam.d/sshd文件 在auth行下方添加: auth required pam_tally.so deny5 unlock_time600 no_lock_time 在account行下方添加: account required pam_tally.s…...
 中的 SEP 参数)
Python打印() 中的 SEP 参数
默认情况下,Python 中 print() 函数的参数之间的分隔符是空格(softspace 功能),可以根据我们的选择对其进行修改并设置为任何字符、整数或字符串。“sep”参数用于实现相同的目的,它仅在python …...

AG9300方案替代|替代AG9300设计Type-C转VGA方案|CS5260设计原理图
AG9300方案替代|替代AG9300设计Type-C转VGA方案|CS5260设计原理图 安格 AG9300是一款实现USB TYPE-C到VGA数据的单片机解决方案转换器。ALGOLTEK AG9300支持USB Type-C显示端口交替模式,AG9300可以将视频和音频流从USB Type-C接口传输到VGA端口。在AG9300࿰…...

力扣-文章浏览
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1148. 文章浏览二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.其他总结前言 一、题目:1148…...

Unity提取场景中的静态文本
有些单机项目开发的时候没有做本地文本配置文件,全部写死在场景的对象上面,简单记录一下怎么提取场景里面的文本并且写入到配置文件里面using System.Collections.Generic;using System.IO;using TMPro;using UnityEditor;using UnityEngine;using Unity…...

Netty常用核心类说明
MessageToByteEncoder MessageToByteEncoder是一个抽象编码器,子类可重写encode方法把对象编码为ByteBuf输出。 MessageToByteEncoder继承自ChannelOutboundHandlerAdapter,encode在出站是被调用。 public class MyMessageEncoder extends MessageToB…...
ingress服务
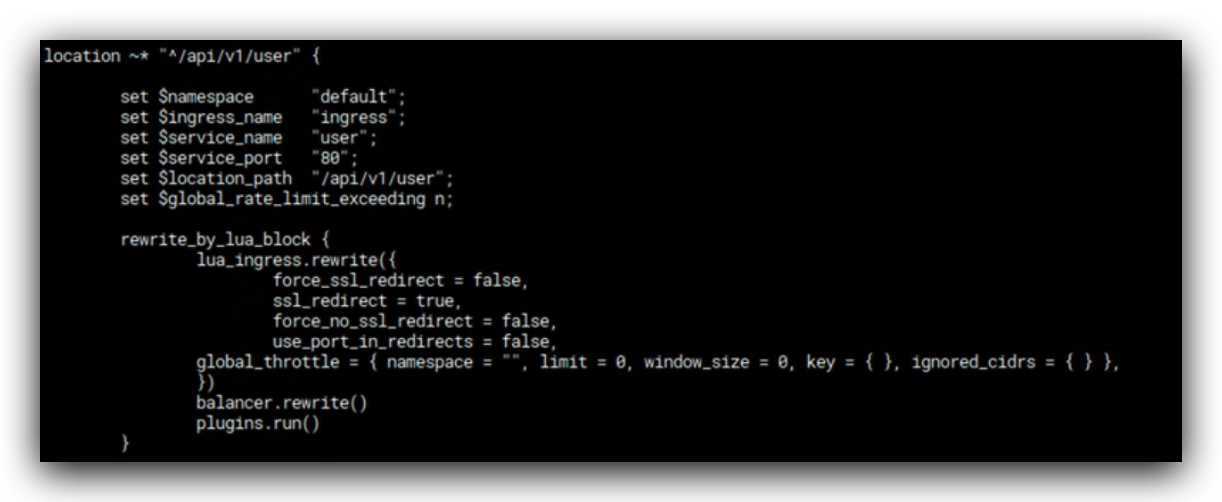
user.default.svc.cluster.local是集群内部service的dns地址,集群外部想访问集群里面的service,可以通过LoadBalaner和NodePort。LoadBalaner可以获得一个公网ip;NodePort在宿主机上开一个端口,访问这个端口会把报文实际的转发到集…...

java 抽象类 详解
目录 一、抽象类概述: 二、抽象方法 : 1.概述 : 2.应用 : 3.特点 : 三、抽象类特点 : 1.关于abstract关键字 : 2.抽象类不能被实例化,只能创建其子类对象 : 3.抽象类子类的两个选择 : 四、抽象类的成员 : 1.成员变量 : 2.成员方…...
MySQL的安装(详解)
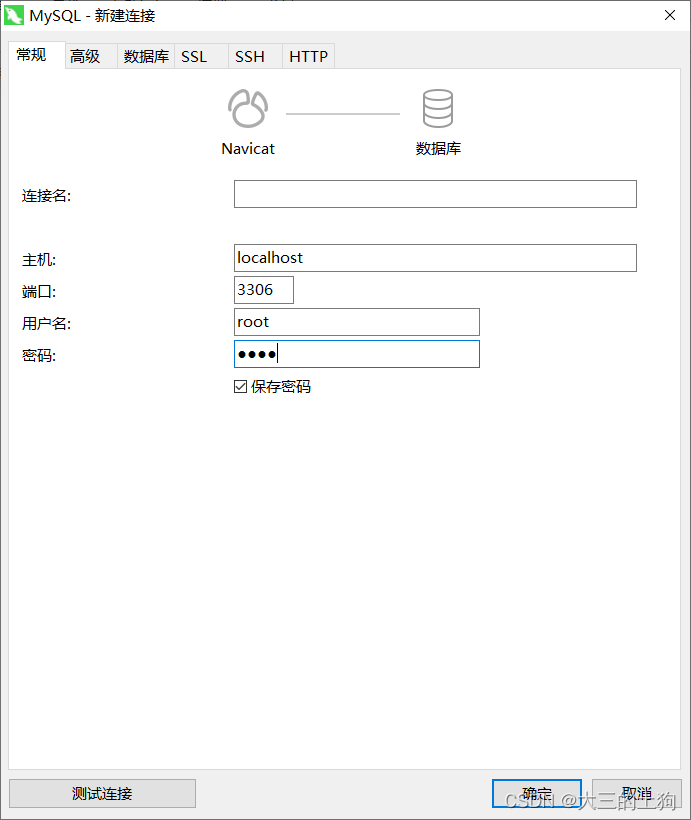
文章目录前言一、yum方式安装1、下载并安装MySQL2、 启动MySQL数据库3、查看MySQL初始密码4、登录数据库5、修改MySQL默认密码6、授予root用户远程管理权限7、输入exit退出数据库二、rpm安装方式1、检查2、卸载mariadb3、安装4、启动5、密码总结前言 本教程为Linux下安装mysql的…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
