【简单图论】CF898 div4 H
Problem - H - Codeforces
题意:

思路:
手玩一下样例就能发现简单结论:
v 离它所在的树枝的根的距离 < m 离这个根的距离时是 YES
否则就是NO
实现就很简单,先去树上找环,然后找出这个根,分别给a 和 b BFS一遍,得出两个dis数组,比较一下即可
对于只有的环情况 和 m = v 的情况需要特判
Code:
#include <bits/stdc++.h>constexpr int N = 2e5 + 10;
constexpr int M = 1e6 + 10;
constexpr int Inf = 1e9;std::queue<int> q1, q2;
std::vector<int> adj[N];int n, a, b;
int top = 0;
int u[N], v[N];
int st[N], r[N];
int dis1[N];
int dis2[N];int find_r(int u, int fa) {if (st[u]) return u;st[u] = 1;for (auto v : adj[u]) {if (v == fa) continue;int t = find_r(v, u);if (t) {r[++ top] = u;st[u] = 2;return t == u ? 0 : t;}}return 0;
}
void bfs1(int u) {memset(dis1, 0x3f, sizeof(dis1));dis1[u]= 0;q1.push(u);while(!q1.empty()) {int u = q1.front();q1.pop();for (auto v : adj[u]) {if (dis1[v] > dis1[u] + 1) {dis1[v] = dis1[u] + 1;q1.push(v);}}}
}
void bfs2(int u) {memset(dis2, 0x3f, sizeof(dis2));dis2[u] = 0;q2.push(u);while(!q2.empty()) {int u = q2.front();q2.pop();for (auto v : adj[u]) {if (dis2[v] > dis2[u] + 1) {dis2[v] = dis2[u] + 1;q2.push(v);}}}
}
void solve() {std::cin >> n >> a >> b;top = 0;while(!q1.empty()) q1.pop();while(!q2.empty()) q2.pop();for (int i = 1; i <= n; i ++) {st[i] = 0;adj[i].clear();}for (int i = 1; i <= n; i ++) {std::cin >> u[i] >> v[i];adj[u[i]].push_back(v[i]);adj[v[i]].push_back(u[i]);}if (a == b) {std::cout << "NO" << "\n";return;}find_r(1, 0);bfs1(b);int miu1 = Inf, ansu = 0;for (int i = 1; i <= n; i ++) {if (st[i] == 2 && miu1 > dis1[i]) {miu1 = dis1[i];ansu = i;}}if (st[b] == 2) {std::cout << "YES" << "\n";return;}bfs2(a);int ans1 = dis2[ansu];int ans2 = miu1;if (ans1 > ans2) std::cout << "YES" << "\n";else std::cout << "NO" << "\n";
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t = 1;std::cin >> t;while(t --) {solve();}return 0;
}
相关文章:

【简单图论】CF898 div4 H
Problem - H - Codeforces 题意: 思路: 手玩一下样例就能发现简单结论: v 离它所在的树枝的根的距离 < m 离这个根的距离时是 YES 否则就是NO 实现就很简单,先去树上找环,然后找出这个根,分别给a 和…...
【大虾送书第十一期】适合新手自学的网络安全基础技能“蓝宝书”:《CTF那些事儿》
目录 🥮写在前面 🥮内容简介 🥮读者对象 🥮专家推荐 🥮目录 🥮文末福利 🦐博客主页:大虾好吃吗的博客 🦐专栏地址:免费送书活动专栏地址 写在前面 CTF比赛是快…...
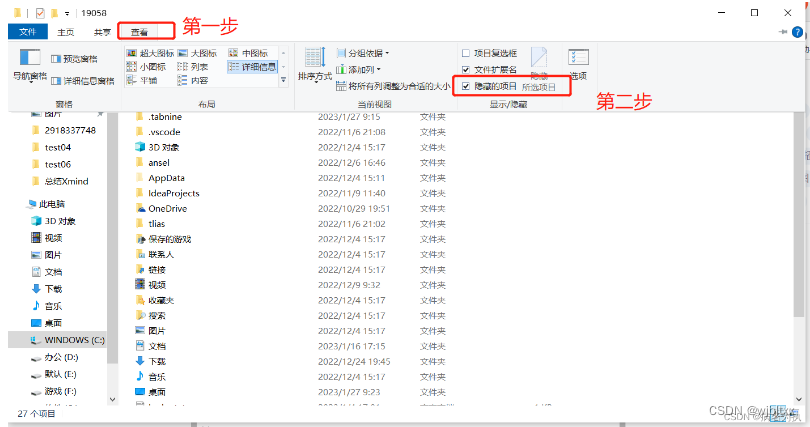
IDEA安装离线插件后重启无法打开
解决方法 1.找到插件安装目录删除插件 插件的位置一般在C:\Users\19058\AppData\Roaming\JetBrains\IntelliJIdea2021.1\plugins 高亮部分是自己电脑的用户位置,把报错前的刚才最新安装的插件删除,再尝试打开idea即可解决该问题 2.补充说明 AppData是个隐…...

论软件的可靠性设计
摘要 2021年6月,我所在的公司中标某集团保险大数据平台一体化研发项目,该项目总投资2000万人民币,项目周期为2年,通过该项目,搭建该集团保险大数据平台,一方面将全国所有保险业务全部入库并保存࿰…...

AG35学习笔记(一):debug串口抓取模组log、debug串口测试AT指令、echo命令通过串口发送16进制数据
目录 一、概述二、抓取模组log2.1 硬件接口2.2 用户登录2.3 相关指令 三、测试AT指令3.1 查看端口3.2 进入模式 四、串口发16进制echo使用 一、概述 二、抓取模组log 在之前记录了通过USB,使用移远工具Qwinlog来抓取log(3.3 抓取模组log)。…...

Python进阶学习----一闭三器
目录 编辑 前言 一.三器 1. 迭代器(Iterator) 1.1 什么是可迭代对象 1.2什么是迭代器 1.3案例演示: 以下是一个简单的迭代器示例,遍历一个列表并打印每个元素: 1.4迭代器总结 2. 生成器(Generat…...

C/S架构学习之TCP客户端
TCP客户端的实现流程:一、创建套接字(socket函数):通信域选择IPV4网络协议、流式套接字; int sockfd socket(AF_INET,SOCK_STREAM,0); 二、填充服务器的网络信息结构体(struct sockaddr_in serveraddr&…...

系统集成|第十二章(笔记)
目录 第十二章 沟通管理12.1 沟通的基本概念12.2 主要过程12.2.1 规划沟通管理12.2.2 管理沟通12.2.3 控制沟通 12.3 常见问题 上篇:第十一章、项目人力资源管理 第十二章 沟通管理 沟通管理在项目计划、执行、监控过程中具有重要的作用,项目经理应该拿…...
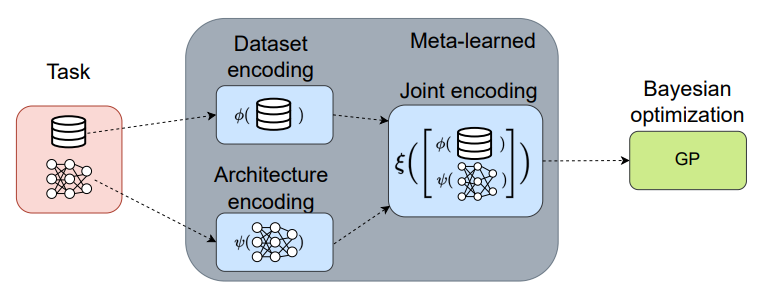
图神经网络(GNN)最新顶会论文汇总【附源码】
得益于强大的建模和分析能力,图神经网络(GNN)在社交网络分析、推荐系统、知识图谱、文本分析、等诸多领域得到了广泛的应用,目前已成为了人工智能领域的热门研究方向。 在今年的各大顶会获奖论文中,图神经网络相关的论…...
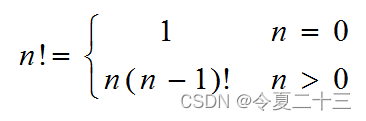
【算法】算法设计与分析 课程笔记 第二章 递归与分治策略
2.1 递归 直接或间接地调用自身的算法称为递归算法。 用函数自身给出定义的函数称为递归函数。 2.1.1 阶乘 首先得想到一个求阶乘的函数: 这个函数的下面那个式子就用到了调用自身,所以可以用递归来实现,将主问题拆分成若干层的子问题&am…...
Java客户端_Apache Curator操作Zookeeper
Curator是 Netflix公司开源的一套ZooKeeper客户端框架。和ZkClient一样,Curator解决了很多ZooKeeper客户端非常底层的细节开发工作,包括连接重连、反复注册Watcher和 NodeExistsException异常等,目前已经成为了Apache的顶级项目,是全世界范围…...

14:00面试,14:07就出来了,问的问题有点变态
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到8月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40%,…...

《你好,C语言》:从另一个视角学习并重新审视C语言的意义
《你好,C语言》:从另一个视角学习并重新审视C语言的意义 尽管C语言诞生了这么多年,但是它依然活跃在开发者一线,不可否认的是C语言的确有它独特的魅力。本文将从一个全新的视角,重新带领大家学习领悟C语言的奥秘&#…...
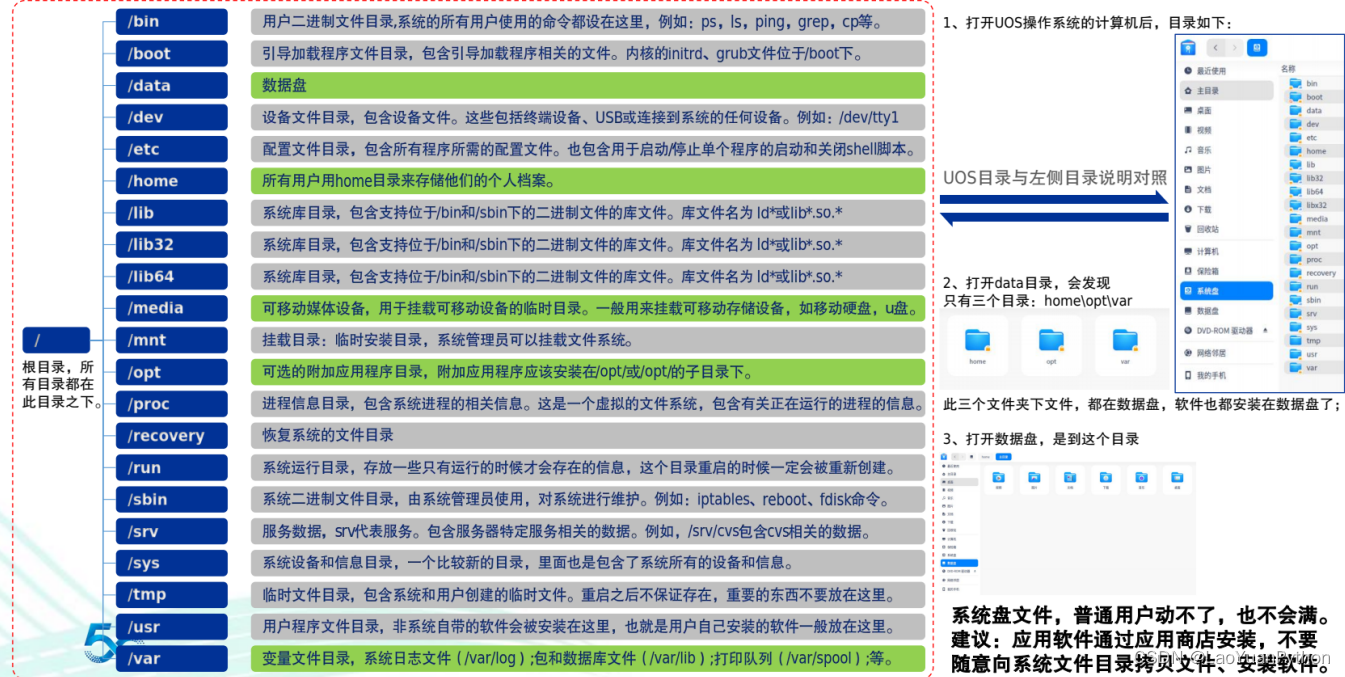
信创之国产浪潮电脑+统信UOS操作系统体验1:硬件及软件常规功能支持情况介绍
一、引言 由于公司要求支持国产信创,最近办公的笔记本电脑换成了软硬件全国产,由于国产操作系统是在开源linux基础上演进的,在换之前,非常担心操作不方便,周边应用软件少,功能差,内心是比较抗拒…...

JAVA学习-全网最详细
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...

基于物联网的农村地区智能微电网系统(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

JavaScript系列从入门到精通系列第九篇:JavaScript中赋值运算符和关系运算符以及Unicode编码介绍
一:赋值运算符 1: 右侧的值可以赋值给左侧的变量。 var a 123; console.log(a);//123 2: var a 10; a a 5; a 5; 上边这两个写法是一样的。 3:- var a 10; a a-5; a - 5; 上边这两个写法是一样的。 4:* …...

租用独立服务器有哪些常见的误区?
租用独立服务器有哪些常见的误区? 如今,租用独立服务器的市场随着idc行业良好的发展趋势而变得越来越广泛,其最明显的地方在于出现了许多的代理商,而成为代理商的门槛非常低,这样一来就会出现许多问题,导致…...

【学习笔记】POJ 3834 graph game
点这里 结论题😅 ,图一乐 结论:如果原图中存在两个边集不交的生成树,那么 Bob \text{Bob} Bob必胜;否则 Alice \text{Alice} Alice必胜 证明有点难😅 首先,考虑维护两颗 不存在红边 的生成树…...

无监督学习算法Kmeans
1. 有监督学习和无监督学习 在机器学习算法中,常把算法分为有监督学习和无监督学习两种。他们之间的区别主要在于输入数据集类型和学习目标。 (1)有监督学习:训练输入的数据需要带有标签,以便算法能够学习输入和输出…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
