【学习笔记】POJ 3834 graph game
点这里
结论题😅 ,图一乐
结论:如果原图中存在两个边集不交的生成树,那么 Bob \text{Bob} Bob必胜;否则 Alice \text{Alice} Alice必胜
证明有点难😅
首先,考虑维护两颗 不存在红边 的生成树,如果 Alice \text{Alice} Alice断掉了其中一颗树上的一条边,将这个树分成两个连通块,那么 Bob \text{Bob} Bob一定可以在另一颗树上选择一条边变成蓝色,使得这个树再次联通,最终两个生成树都只由蓝边构成
其次,如果原图中不存在这样的两颗生成树,则考虑某次 Alice \text{Alice} Alice操作时, Bob \text{Bob} Bob胜利的条件:将所有蓝色的边 复制一遍,使得存在两个边集不交的生成树。假设存在某种策略,使得 Bob \text{Bob} Bob在某次操作后满足了这个条件,那么 Alice \text{Alice} Alice可以照搬 Bob \text{Bob} Bob的策略,使得某次操作后将红边复制一遍,使得存在两个边集不交的生成树。因此 Alice \text{Alice} Alice存在可以让红边构成一颗生成树的策略。又因为原图中不存在两个边集不交的生成树,因此 Bob \text{Bob} Bob无法胜利
有点绞
发现 ( 30 9 ) \binom{30}{9} (930)比较小,直接暴搜即可。
#include<cstdio>
#include<iostream>
#define ll long long
#define pb push_back
#define fi first
#define se second
#define db double
#define ull unsigned long long
#define inf 0x3f3f3f3f
using namespace std;
int n,m,fa[10],fa2[10],U[30],V[30],s[30];
int find(int x){return fa[x]==x?x:find(fa[x]);
}
int check(){for(int i=0;i<n;i++)fa2[i]=fa[i],fa[i]=i;int tot=0;for(int i=0;i<m;i++){if(s[i]==0){int x=find(U[i]),y=find(V[i]);if(x!=y)fa[x]=y,tot++;}}if(tot==n-1){return 1;}for(int i=0;i<n;i++)fa[i]=fa2[i];return 0;
}
int dfs(int x,int y){if(y==n-1)return check();for(int i=x;i<m;i++){int a=find(U[i]),b=find(V[i]);if(a==b)continue;fa[a]=b,s[i]=1;if(dfs(i+1,y+1))return 1;fa[a]=a,s[i]=0;}return 0;
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);while(cin>>n>>m){if(n==-1&&m==-1)break;for(int i=0;i<n;i++)fa[i]=i;for(int i=0;i<m;i++)cin>>U[i]>>V[i],s[i]=0;cout<<(dfs(0,0)?"YES":"NO")<<"\n";}
}
相关文章:

【学习笔记】POJ 3834 graph game
点这里 结论题😅 ,图一乐 结论:如果原图中存在两个边集不交的生成树,那么 Bob \text{Bob} Bob必胜;否则 Alice \text{Alice} Alice必胜 证明有点难😅 首先,考虑维护两颗 不存在红边 的生成树…...

无监督学习算法Kmeans
1. 有监督学习和无监督学习 在机器学习算法中,常把算法分为有监督学习和无监督学习两种。他们之间的区别主要在于输入数据集类型和学习目标。 (1)有监督学习:训练输入的数据需要带有标签,以便算法能够学习输入和输出…...
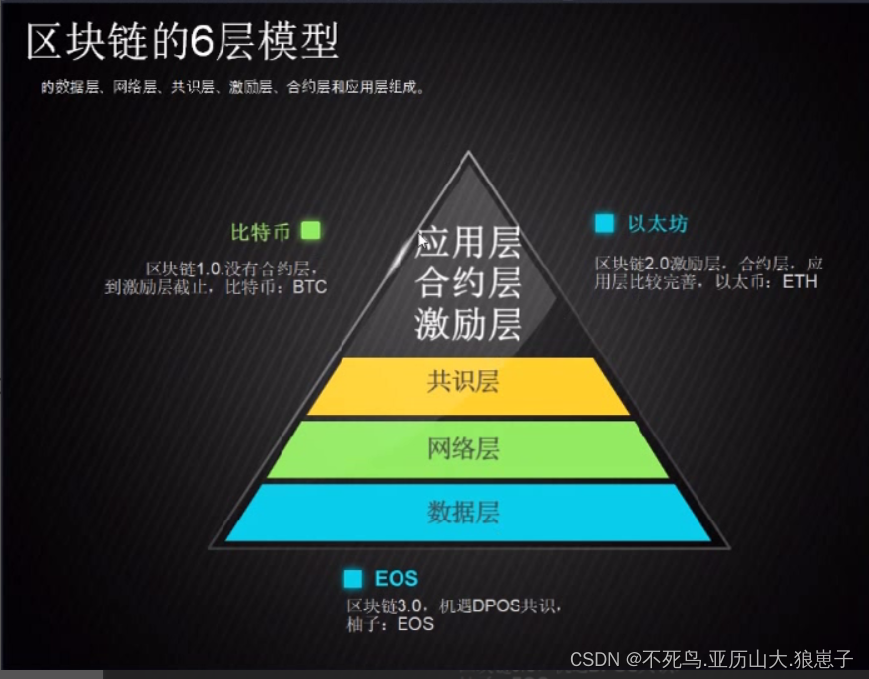
区块链(4):区块链技术模型介绍
1 区块链白皮书中的公有链,私有链,联盟链概念介绍 区块链系统根据应用场景和设计体系的不同,一般分为公有链、联盟 链和专有链(私有链)。其中: 公有链的各个节点可以自由加入和退出网络,并参加链上数据的读 写,运行时…...

go语言 rune 类型
ASCII 码只需要 7 bit 就能完整地表示,但只能表示英文字母在内的 128 个字符,为了表示世界上大部分的文字系统,发明了 Unicode ,它是 ASCII 的超集,包含世界上书写系统中存在的所有字符,并且为每个代码分配…...
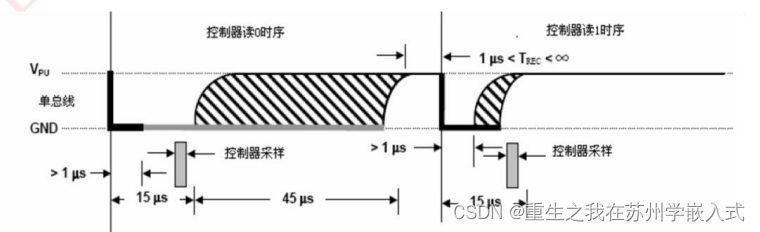
DS18B20温度传感器
DS18B20简介 DS18B20 是由 DALLAS 半导体公司推出的一种的“一线总线(单总线)”接口的温度传感器 这种一线总线就是 三线制 SPI DS18B20的 配置寄存器: TM 是测试位,出厂设置就被设置为0,不需要改动, R1、R…...

LeetCode322. 零钱兑换
322. 零钱兑换 文章目录 [322. 零钱兑换](https://leetcode.cn/problems/coin-change/)一、题目二、题解方法一:完全背包二维数组方法二:一维数组 三、注意 一、题目 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 a…...

AUTOSAR扫盲贴--不是黑神话【基本概念和方法论】
猴子纵有72搬变化,也跳不出如来的手掌 目录 1. 引言 2. AUTOSAR的基本概念 2.1. AUTOSAR的架构和组成部分 2.2. AUTOSAR的规范和...

python抠图(去水印)开源库lama-cleaner入门应用实践
1. 关于 Lama Cleaner Lama Cleaner 是由 SOTA AI 模型提供支持的免费开源图像修复工具。可以从图片中移除任何不需要的物体、缺陷和人,或者擦除并替换(powered by stable diffusion)图片上的任何东西。 特征: 完全免费开源&am…...

Nginx可视化管理工具结合cpolar实现远程访问内网服务
前言 Nginx Proxy Manager 是一个开源的反向代理工具,不需要了解太多 Nginx 或 Letsencrypt 的相关知识,即可快速将你的服务暴露到外部环境,并且支持 SSL 配置。基于 Tabler 的美观且安全的管理界面,无需了解 Nginx 即可轻松创建转发域、重定…...

CCC数字钥匙设计【BLE】 --建立安全测距
1、建立安全测距Establish Secure Ranging 车端总共有三种建立安全测距的方式,具体如下: 1) Optimal Flow 2) Sub-Optimal Flow 3) Ranging Recovery Flow 为了确定建立安全测距需要执行哪条流程,车辆需要进行以下流程选择。当车辆和设备…...

Ubuntu22.04 Opencv4.5.1 CPU和GPU编译攻略,Opencv CPU和GPU编译保姆教程 亲自测试。
1、安装opencv依赖 安装时最好更换一下源。 sudo apt-get -y update sudo apt-get -y install cmake git libgtk2.0-dev pkg-config libavcodec-dev libavformat-dev libswscale-dev sudo apt-get -y install libgtk-3-dev gfortran openexr libatlas-base-dev python3-dev pyt…...

常识判断 --- 党史
目录 中共1~3大 例题 国民党 例题 中共4~5大 例题 中共起义~会议 例题 中共六届六中全会(1938年9月) 中共七大(1945年4月) 例题 中共七届二中全会 例题 中共8~10大 中共11~12届全会 例题 中共13~14大 …...

Rust 基础再理解
Rust堆栈 Rust中各种类型的值默认都存储在栈中,除非显式地使用Box::new()将它们存放在堆上,但数据要存放在栈中,要求其数据类型的大小已知。对于静态大小的类型,可直接存储在栈上,如裸指针、布尔、字符、整数浮点数&a…...
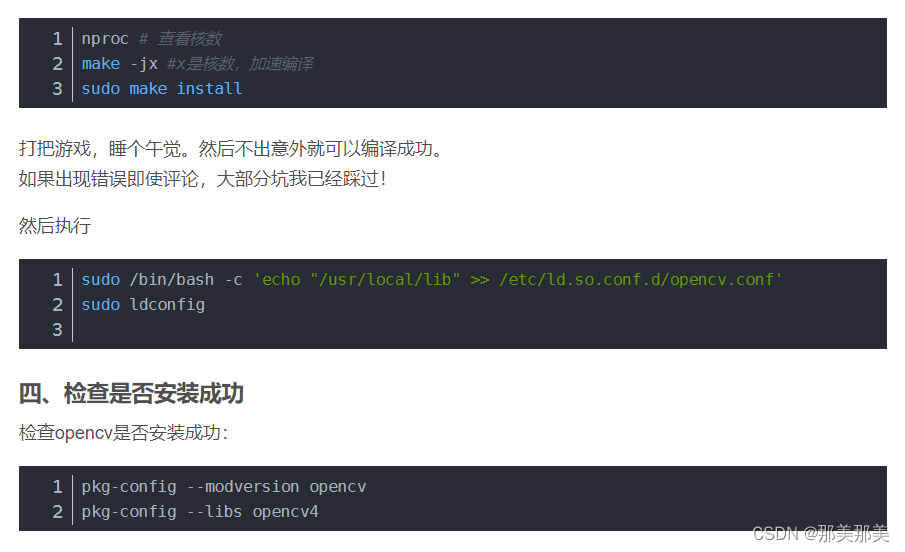
Opencv cuda版本在ubuntu22.04中安装办法,解决Could NOT find CUDNN的办法
文章目录 概要下载cuda的runfile版本配置环境变量官网下载cudann安装Opencv依赖包下载opencv和opencv_contrib并解压准备编译安装anaconda环境执行编译命令安装OpenCV并检查是否安装成功 概要 解决以下安装问题: -- Could NOT find CUDNN: Found unsuitable versi…...

全网首发YOLOv8暴力涨点:Gold-YOLO,遥遥领先,超越所有YOLO | 华为诺亚NeurIPS23
💡💡💡本文独家改进:提出了全新的信息聚集-分发(Gather-and-Distribute Mechanism)GD机制,Gold-YOLO,替换yolov8 head部分 实现暴力涨点 Gold-YOLO | 亲测在多个数据集能够实现大幅涨点 💡💡💡Yolov8魔术师,独家首发创新(原创),适用于Yolov5、Yolov7、…...

BD就业复习第四天
1. 布隆过滤器怎么实现去重 布隆过滤器是一种用于快速检查一个元素是否可能存在于一个大集合中的数据结构,但它并不适用于精确去重。因为布隆过滤器具有一定的误判率(可能会将不存在的元素误判为存在),所以不能确保完全的去重。但…...
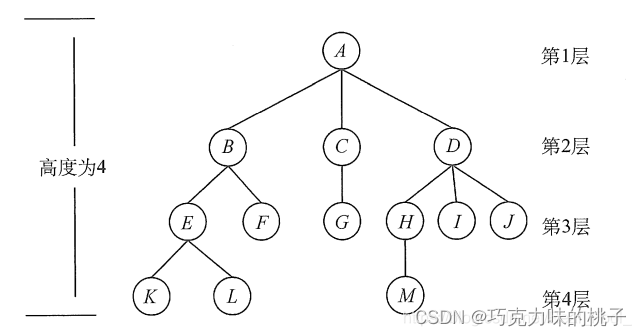
数据结构 | 树
树 树是n(n>0)个结点的有限集。当n 0时,称为空树。在任意一棵非空树中应满足: 有且仅有一个特定的称为根的结点。当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm&#…...
Android11 适配
一、修改targetSdkVersion为30 将build.gradle的目标版本targetSdkVersion修改为30(Android 11) targetSdkVersion 30Android11的改变改变主要影响以Adnroid11 为目标版本的应用(targetSdkVersion>30才有影响),和所…...
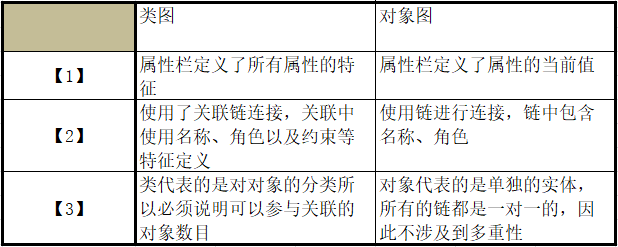
UML基础与应用之对象图
什么是对象图? 对象图表示一组对象及它们之间的关系,是某一时刻系统详细信息的快照,描述系统交互的静态图形,它由协作的对象组成,但不包含在对象之间传递的任何消息。因为对象是类的实例化,所以说某一时刻…...

英码科技精彩亮相火爆的IOTE 2023,多面赋能AIoT产业发展!
9月20日至22日,在这金秋飒爽的季节,为期三天的IOTE 2023第二十届国际物联网展深圳站在深圳国际会展中心盛大举行。英码科技精彩亮相本届展会,并在同期举办的AIoT视觉物联产业生态大会发表了主题演讲,与生态伙伴们共同探讨AIoT产业…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
