数据结构 | 树
树
树是n(n>=0)个结点的有限集。当n = 0时,称为空树。在任意一棵非空树中应满足:
- 有且仅有一个特定的称为根的结点。
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每个集合本身又是一棵树,并且称为根的子树。
概念
树的高、深度vs结点的高、深度
| 高度:从下到上 | 深度:从上到下 |
|---|---|
| 根节点为第0层:高度:数结点数,深度:数路径 | 树从根结点开始往下数,叶子结点所在的最大层数 |
| 树:高度等于深度(根节点为第一层) | 结点高度不一定等于深度(叶子结点编号是0还是1) |
树的高度和深度 | 结点的高度和深度_树的高度从0开始还是1_Ann's Blog的博客-CSDN博客
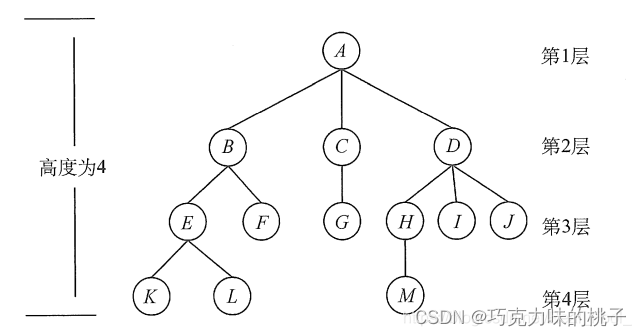
祖先:考虑结点K。根A到结点K的唯一路径上的任意结点,称为结点K的祖先。如结点B是结点K的祖先,而结点K是结点B的子孙。
双亲&孩子:路径上最接近结点K的结点E称为K的双亲,而K为结点E的孩子。
兄弟:有相同双亲的结点称为兄弟,如结点K和结点L有相同的双亲E,即K和L为兄弟。
堂兄弟:双亲在同一层的结点互为堂兄弟,图中结点G与E,F,H,I,J互为堂兄弟。
度:树中一个结点的孩子个数称为该结点的度,树中结点的最大度数称为树的度。如结点B的度为2,结点D的度为3,树的度为3。
分支结点:度大于0的结点称为分支结点(又称非终端结点);
叶子结点:度为0(没有子女结点)的结点称为叶子结点(又称终端结点)。
有序树和无序树。树中结点的各子树从左到右是有次序的,不能互换,称该树为有序树,否则称为无序树。
路径和路径长度。树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。
注意:由于树中的分支是有向的,即从双亲指向孩子,所以树中的路径是从上向下的,同一双亲的两个孩子之间不存在路径。
森林。森林是m (m≥0)棵互不相交的树的集合。森林的概念与树的概念十分相近,因为只要把树的根结点删去就成了森林。反之,只要给m棵独立的树加上一个结点,并把这m棵树作为该结点的子树,则森林就变成了树。
相关文章:

数据结构 | 树
树 树是n(n>0)个结点的有限集。当n 0时,称为空树。在任意一棵非空树中应满足: 有且仅有一个特定的称为根的结点。当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm&#…...
Android11 适配
一、修改targetSdkVersion为30 将build.gradle的目标版本targetSdkVersion修改为30(Android 11) targetSdkVersion 30Android11的改变改变主要影响以Adnroid11 为目标版本的应用(targetSdkVersion>30才有影响),和所…...
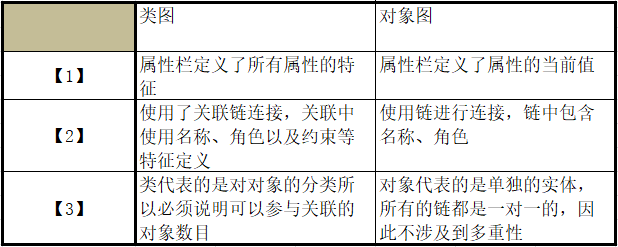
UML基础与应用之对象图
什么是对象图? 对象图表示一组对象及它们之间的关系,是某一时刻系统详细信息的快照,描述系统交互的静态图形,它由协作的对象组成,但不包含在对象之间传递的任何消息。因为对象是类的实例化,所以说某一时刻…...

英码科技精彩亮相火爆的IOTE 2023,多面赋能AIoT产业发展!
9月20日至22日,在这金秋飒爽的季节,为期三天的IOTE 2023第二十届国际物联网展深圳站在深圳国际会展中心盛大举行。英码科技精彩亮相本届展会,并在同期举办的AIoT视觉物联产业生态大会发表了主题演讲,与生态伙伴们共同探讨AIoT产业…...
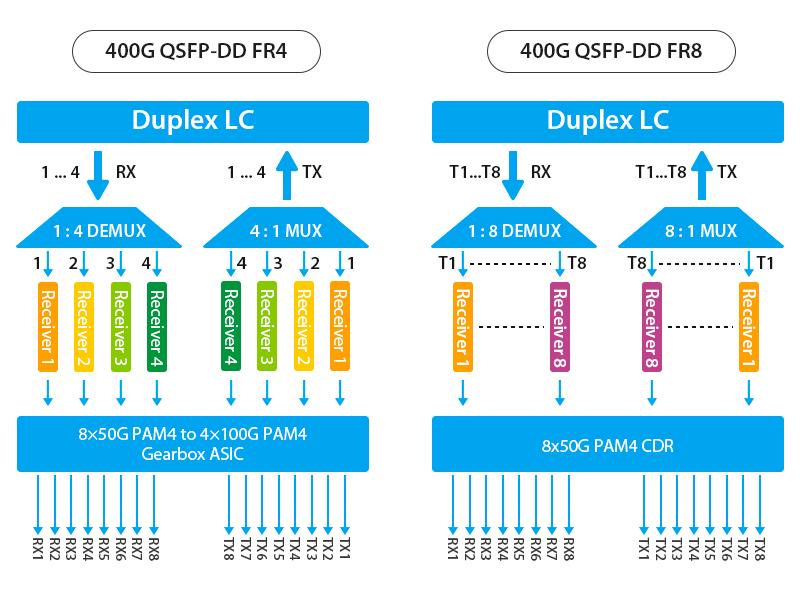
400G QSFP-DD FR4 与 400G QSFP-DD FR8光模块:哪个更适合您的网络需求?
QSFP-DD 光模块随着光通信市场规模的不断增长已成为400G市场中客户需求量最高的产品。其中400G QSFP-DD FR4和400G QSFP-DD FR8光模块都是针对波分中距离传输(2km)的解决方案,它们之间有什么不同?应该如何选择应用?飞速…...
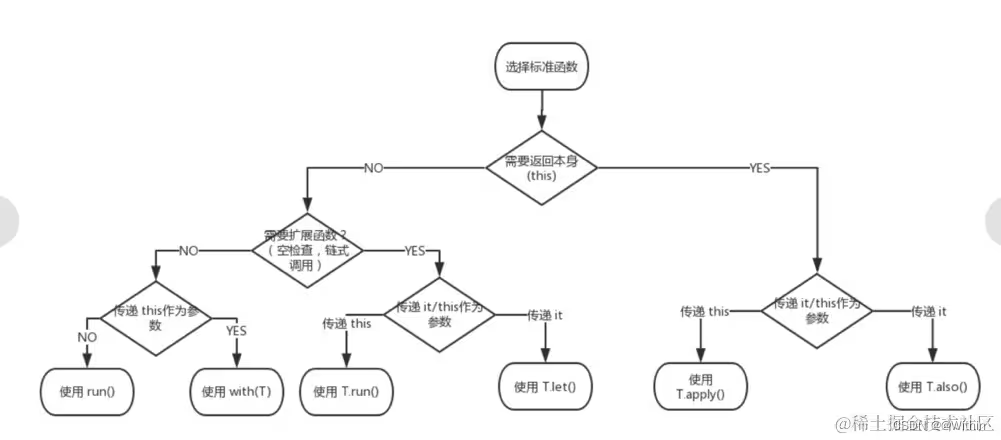
【Android】Kotlin 中的 apply、let、with、also、run 到底有啥区别?
一、图示 二、apply apply 函数接收一个对象并返回该对象本身。它允许您在对象上执行一些操作,同时仍然返回原始对象。 这个函数的语法为: fun <T> T.apply(block: T.() -> Unit): T 其中,T 是对象的类型,block 是一…...

设计模式——职责链模式
职责链模式 职责链模式职责链模式解决什么问题?职责链模式实现 职责链模式 使多个对象都有机会处理请求,从而避免请求的发送者和接收者之间的耦合关系。将这个对象练成一条链,并沿着这条链传递该请求,知道有一个对象处理它为止 …...

小程序自定义tabbar,中间凸起
微信小程序自带tabbar,但无法实现中间按钮凸起样式和功能,因此按照设计重新自定义一个tabbar 1、创建tabbar文件,与pages同级创建一个文件夹,custom-tab-bar,里面按照设计图将底部tabbar样式编写 <view class"tab-bar&q…...

数据结构-顺序栈C++示例
栈(stack)是限定仅在表尾进行插入或删除操作的线性表。 对栈来说,表尾端称为栈顶(top), 表头端称为栈底(bottom),不含元素的空表称为空栈。 假设栈 S ( a 1 , a 2 , a 3 , ⋯ , a n ) S(a_1,a_2,a_3,\cdots,a_n) S(a1,a2,a3,⋯,an…...
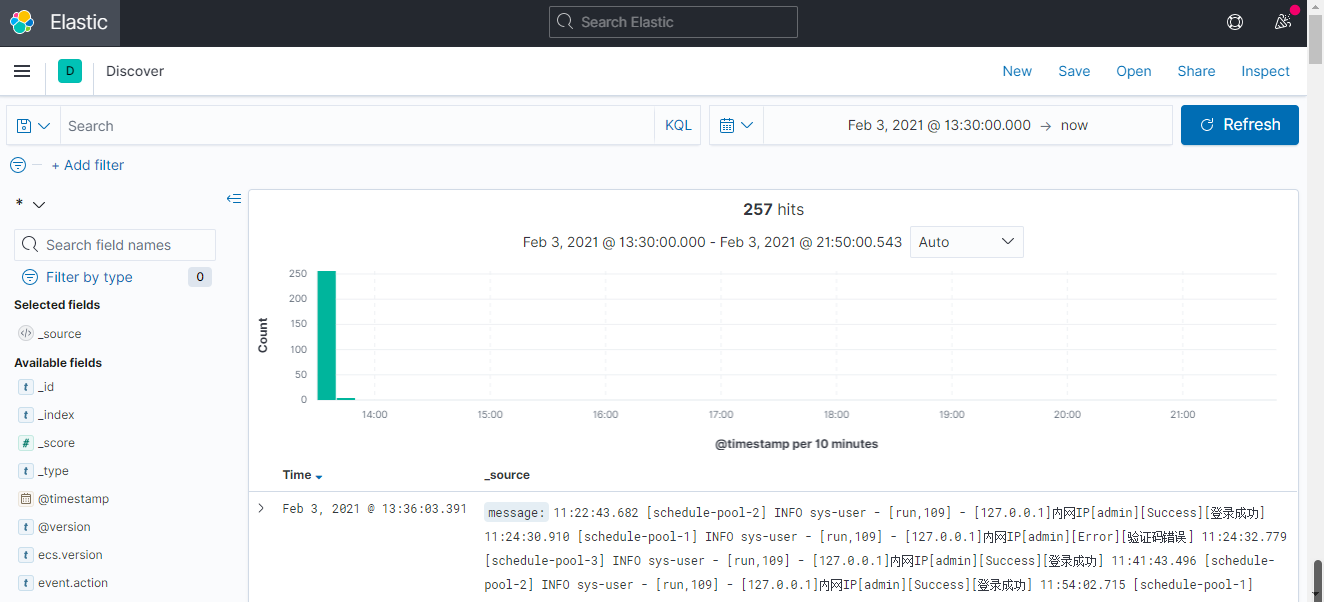
若依cloud -【 100 ~ 103 】
100 分布式日志介绍 | RuoYi 分布式日志就相当于把日志存储在不同的设备上面。比如若依项目中有ruoyi-modules-file、ruoyi-modules-gen、ruoyi-modules-job、ruoyi-modules-system四个应用,每个应用都部署在单独的一台机器里边,应用对应的日志的也单独存…...

可转债实战与案例分析——成功的和失败的可转债投资案例、教训与经验分享
实战与案例分析——投资案例研究 股票量化程序化自动交易接口 一、成功的可转债投资案例 成功的可转债投资案例提供了有价值的经验教训,以下是一个典型的成功案例: 案例:投资者B的成功可转债投资 投资者B是一位懂得风险管理的投资者&#…...
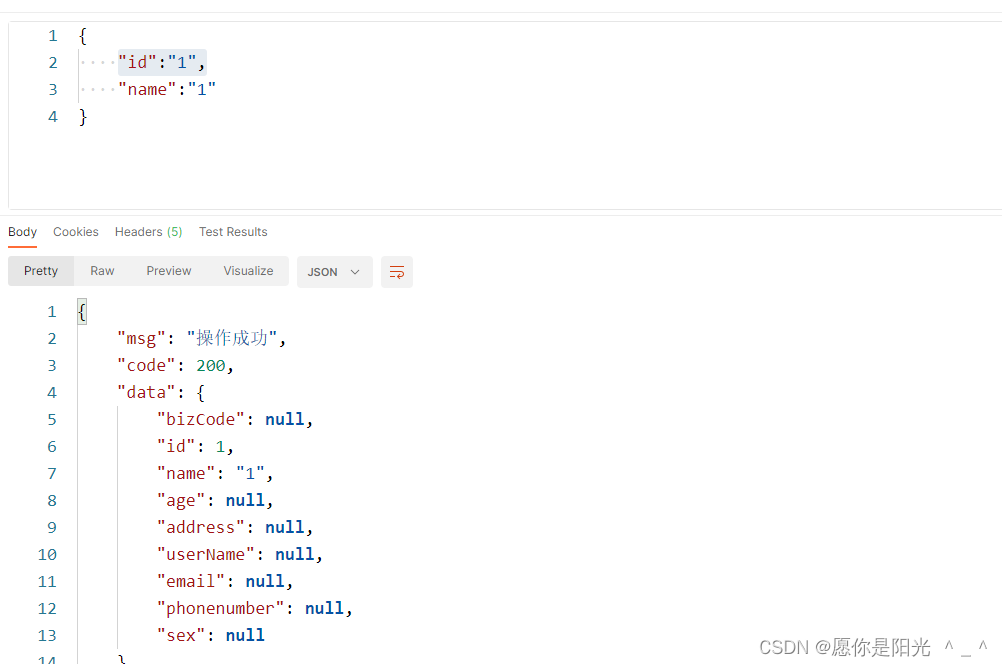
@NotNull注解不生效,全局异常处理
1.引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-validation</artifactId><version>3.1.2</version> </dependency> 2:实体类 实体类属性加上NotNull注解…...

【办公自动化】使用Python一键往Word文档的表格中填写数据(文末送书)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
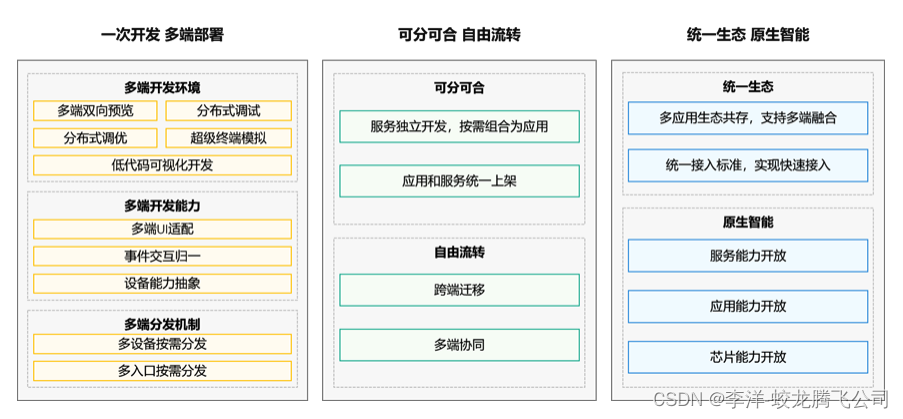
OpenHarmony应用核心技术理念与需求机遇简析
一、核心技术理念 图片来源:OpenHarmony官方网站 二、需求机遇简析 新的万物互联智能世界代表着新规则、新赛道、新切入点、新财富机会;各WEB网站、客户端( 苹果APP、安卓APK)、微信小程序等上的组织、企业、商户等;OpenHarmony既是一次机遇、同时又是一次大的挑战&…...

让Pegasus天马座开发板实现超声波测距
在完成《让Pegasus天马座开发板用上OLED屏》后,我觉得可以把超声波测距功能也在Pegasus天马座开发板上实现。于是在箱子里找到了,Grove - Ultrasonic Ranger 这一超声波测传感器。 官方地址: https://wiki.seeedstudio.com/Grove-Ultrasonic_Ranger 超声…...

C++11 多线程学习
C11学习 一、多线程 1、模板线程是以右值传递的 template <class Fn, class... Args> explicit thread(Fn&& fn, Args&&... args)则需要使用到std::ref和std::cref很好地解决了这个问题,std::ref 可以包装按引用传递的值。 std::cref 可以…...

数学公式测试
MVP变换 MVP变换用来描述视图变换的任务,即将虚拟世界中的三维物体映射(变换)到二维坐标中。 MVP变换分为三步: 模型变换(model tranformation):将模型空间转换到世界空间(找个好的地方,把所…...

机器学习——SVM(支持向量机)
0、前言: SVM应用:主要针对小样本数据进行学习、分类和回归(预测),能解决神经网络不能解决的过学习问题,有很好的泛化能力。(注意:SVM算法的数学原理涉及知识点比较多,所…...

【李沐深度学习笔记】基础优化方法
课程地址和说明 基础优化方法p2 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 基础优化方法 在讲具体的线性回归实现之前,要先讲一下基础的优化模型的方法 梯度下降 当模型没有显示解(…...

tmux 配置vim风格按键,支持gbk编码
vim修改~/.tmux.conf文件,没有则新增,添加如下内容。默认前缀更改为Ctrla。强烈建议更换Caps lock键位与Ctrl键位,用过的都说好,换过就回不来了。 unbind C-b set -g prefix C-a bind a send-prefixset -sg escape-time 1bind r …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
