机器学习——SVM(支持向量机)
0、前言:
- SVM应用:主要针对小样本数据进行学习、分类和回归(预测),能解决神经网络不能解决的过学习问题,有很好的泛化能力。(注意:SVM算法的数学原理涉及知识点比较多,所以应用比理解更重要)
- 原理:由二分类问题引出,如下图,问题是找到一条最宽的路劲划分两种分类,且路径1/2处的直线就是最优的直线。

进而将问题由二维(x轴和y轴)特征数据的分类拓展到更高维度的分类问题中,将问题转换为了多维问题,就会涉及向量和求极值,最终将支持向量的优化目标就由间隔最大化问题转化为了标准凸优化问题(标准凸优化是计算机当中数学问题的描述),然后就可以得到支持向量机算法。 - 支持向量机算法:
输入:m条训练数据S = {(x1,y1),(x2,y2),…,(xm,ym)}
前提:训练数据中正负采样存在分离平面
模型假设:H (关于w,x,b)
计算w和b的最优解
输出模型:H - 支持向量机的对偶:将求解代约束的凸优化问题转化为求解它的对偶问题。然后借助拉格朗日求解对应的函数,这个函数的意义对于二维特征来说就是一条可以划分二分类问题的最优直线,对于三维特征来说就是一个可以划分空间中二分类问题的最优平面。
- 如下图所示就是二维特征的SVM所求直线A

- 如下图就是多维特征求最优划分的平面,因为在原始空间中,无法用一条直线划分,进而采用核技巧,将问题放到高维空间,进而划分数据,核技巧也称核变换是解决低纬度不可分问题的一个技巧。

- 支持向量机当中会有一些核函数,有线性核函数和高斯核函数。
1、支持向量机的分类示例:
- 目的:通过sklearn.datasets中的make_blobs生成2个类型的聚类,然后用SVC模型训练数据,借助模型的属性生成分类最优分界线,同时生成支持向量对应的直线
- 代码
# 导库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# SVM分类和回归库
from sklearn.svm import SVC,SVR
# 生成二分类数据
from sklearn.datasets import make_blobs
data,target = make_blobs(centers=2)
plt.scatter(data[:,0],data[:,1],c=target)
# 训练数据
# pd.DataFrame(data).head()
# data.shape,target.shape
sv = SVC(C=1,kernel='linear')
'''
SVC当中的参数说明:
1、C:越大表示约分类越严格,对于一些噪声就不%%sh略,可能会导致分类效果差
2、kernel:核函数,一般选默认的rbf(高斯核函数),建议使用默认,
此外还有:linear(线性核函数)、poly(多项式核函数)等
'''
sv.fit(data,target)# 画出通过SVM训练之后的最优分界线
# w1*x1+w2*x2+b=0
# 首先获取斜率和截距
# sv.coef_[0] # array([-0.69045562, -0.92961922])
# sv.coef_.shape # (1, 2)
w1,w2 = sv.coef_[0]
b = sv.intercept_[0]
# 画分界线
plt.scatter(data[:,0],data[:,1],c=target)
x1 = np.linspace(-7,-2,100)
x2 = -1 * (w1*x1+b)/w2
plt.plot(x1,x2,c='r')
# 画支持向量
x1_s = sv.support_vectors_[:,0]
x2_s = sv.support_vectors_[:,1]
plt.scatter(x1_s,x2_s,s=200,alpha=0.3,c='b')
# 画支持向量对应的直线,用虚线表示
b1 = -1*(w1*x1_s[1]+w2*x2_s[1])
b2 = -1*(w1*x1_s[2]+w2*x2_s[2])
x2_1 = -1 * (w1*x1+b1)/w2
x2_2 = -1 * (w1*x1+b2)/w2
plt.plot(x1,x2_1,linestyle='--',linewidth=5,c='r')
plt.plot(x1,x2_2,linestyle='--',linewidth=5,c='r')- 结果

2、支持向量机回归示例:
- 目的:用SVM算法中的SVR预测sin函数
- 代码:
# 导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.svm import SVR
# 制作训练数据
x = np.random.random(150)*10
y = np.sin(x)# 添加噪声
y[::5] += np.random.randn(30)*0.1plt.scatter(x,y)
# 制作测试数据
x_test = np.linspace(0,10,100)
# 训练数据
sv_line = SVR(kernel='linear')
sv_line.fit(x.reshape(-1,1),y)
y_line_pred = sv_line.predict(x_test.reshape(-1,1))sv_poly = SVR(kernel='poly')
sv_poly.fit(x.reshape(-1,1),y)
y_poly_pred = sv_poly.predict(x_test.reshape(-1,1))sv_rbf = SVR(kernel='rbf')
sv_rbf.fit(x.reshape(-1,1),y)
y_rbf_pred = sv_rbf.predict(x_test.reshape(-1,1))
# 画图
plt.scatter(x,y)
plt.plot(x_test,y_line_pred,label='line',c='r')
plt.plot(x_test,y_poly_pred,label='ploy')
plt.plot(x_test,y_rbf_pred,label='rbf')
plt.legend(loc='lower left')
- 结果:

总结:
- 对应二维平面不可分的数据,使用高斯核函数(kernel=‘rbf’)是是最好的选择
相关文章:

机器学习——SVM(支持向量机)
0、前言: SVM应用:主要针对小样本数据进行学习、分类和回归(预测),能解决神经网络不能解决的过学习问题,有很好的泛化能力。(注意:SVM算法的数学原理涉及知识点比较多,所…...

【李沐深度学习笔记】基础优化方法
课程地址和说明 基础优化方法p2 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 基础优化方法 在讲具体的线性回归实现之前,要先讲一下基础的优化模型的方法 梯度下降 当模型没有显示解(…...

tmux 配置vim风格按键,支持gbk编码
vim修改~/.tmux.conf文件,没有则新增,添加如下内容。默认前缀更改为Ctrla。强烈建议更换Caps lock键位与Ctrl键位,用过的都说好,换过就回不来了。 unbind C-b set -g prefix C-a bind a send-prefixset -sg escape-time 1bind r …...
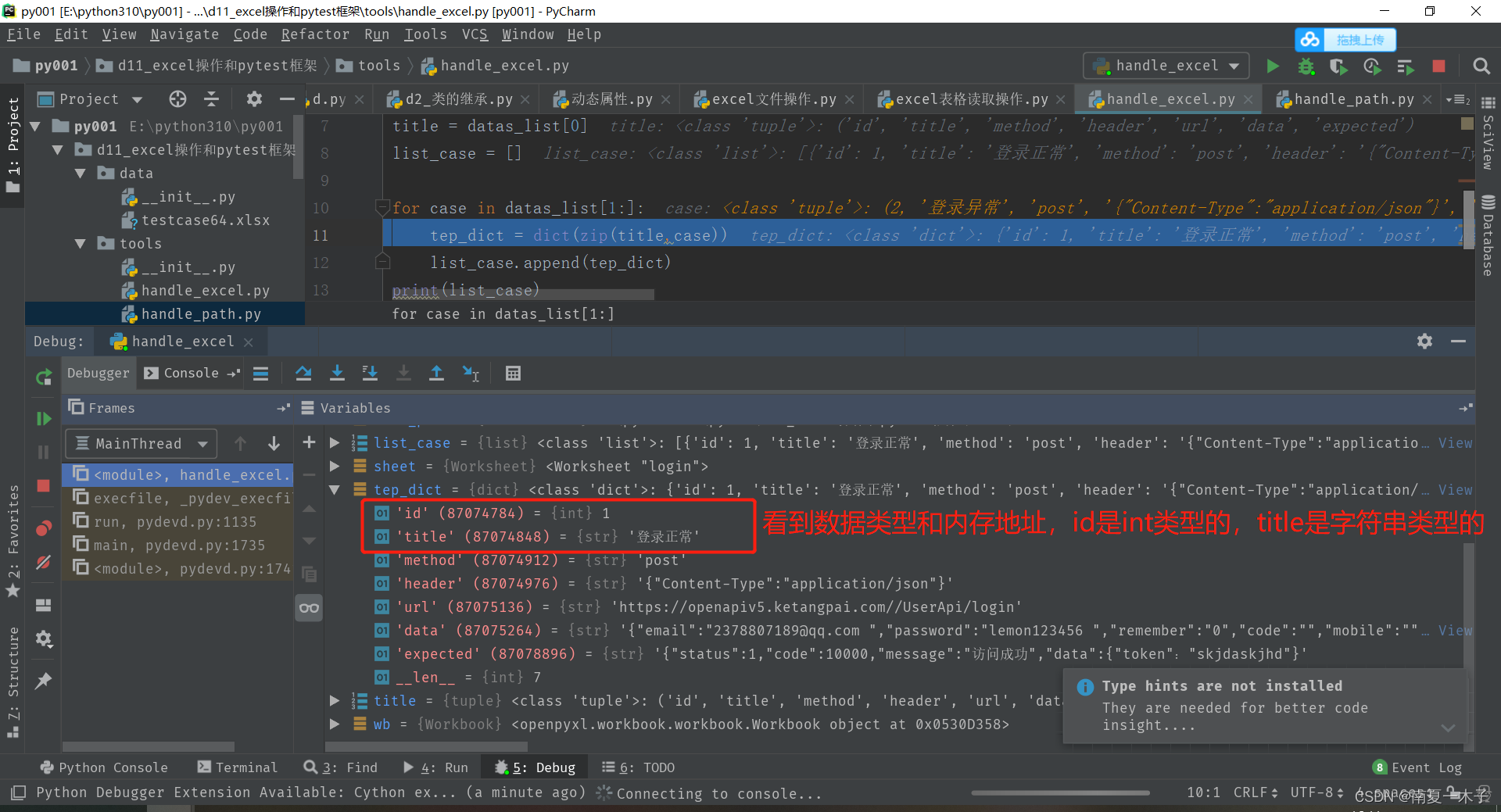
Python —— excel文件操作(超详细)
背景 很多公司还是用excel去管理测试用例的,所以为了减少重复繁琐的导出导出工作,学会如何用代码操作excel表格很实用~ 1、读取excel文件基本步骤 1、操作excel的一些库 1、xlrd:读取库,xlwt:写入,现在…...
什么是AI问答机器人?它的应用场景有哪些?
近年来,由于技术的进步和对个性化客户体验的需求不断增长,AI问答机器人也是获得了巨大的关注。AI问答机器人,也被称为AI聊天机器人,是一种旨在模拟人类对话并通过基于文本或语音的界面与用户交互的计算机程序。其能够自动执行各种…...

静态文件
静态文件 静态文件配置 - settings.py中 1,配置静态文件的访问路径【该配置默认存在】 通过哪个url地址找静态文件 STATIC URL‘/static/’ 说明 指定访问静态文件时是需要通过/static/xxx或http://127.0.0.1:8000/static/xxx [xxx表示具体的静态资源位置] 模…...

Centos7 自部署中间件开机启动,以及java应用开机启动方法
一、zookeeper cd /etc/rc.d/init.d/ touch zookeeper chmod x zookeeper vi zookeeper#以下为内容,自行修改 路径#!/bin/bash ##chkconfig:2345 10 90#description:service zookeeper #修改为自己的目录 export ZOO_LOG_DIR/data/apache-zookeeper-3.7.0/logs…...

密度估计公式
极大似然估计: y p ( x 1 , x 2 , x 3 , . . . , x n ) 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 y p(x_1,x_2,x_3,...,x_n) \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1…...
)
2023 ICPC 网络赛 第一场(补题:F)
7题罚时879, 队排235,校排79。 除了I题dp没注意空间限制第一发没有用滚动数组MLE,以及G题启发式合并脑抽用set当容器T一发,以及K没注意是平方的期望白wa4发这些应当避免的失误外,基本满意。剩下的题基本都是当时写不出…...

MySQL慢查询优化、日志收集定位排查、慢查询sql分析
MySQL慢查询日志收集、定位,慢查询分析、排查。 一 MySQL慢查询定位 1. 确定是否已开启慢查询日志 查看慢查询日志是否已经被开启: SHOW VARIABLES LIKE slow_query_log; 如果返回值是OFF,你需要开启它。 2. 开启慢查询日志 你可以临时在运…...

HZOJ-266:表达式计算
题目描述 给出一个表达式,其中运算符仅包含 ,-,*,/,^ 要求求出表达式的最终值。 数据可能会出现括号情况,还有可能出现多余括号情况,忽略多余括号,正常计算即可; 数据保证不会出现大于 max long int 的数据࿱…...

JavaScript学习小结
变量声明:使用var关键字,变量没有类型,但值有类型(弱类型语言) 数据类型: ①number ②string(单引号,双引号都可以表示字符串) ③boolean ④Object类型 ⑤undefine…...
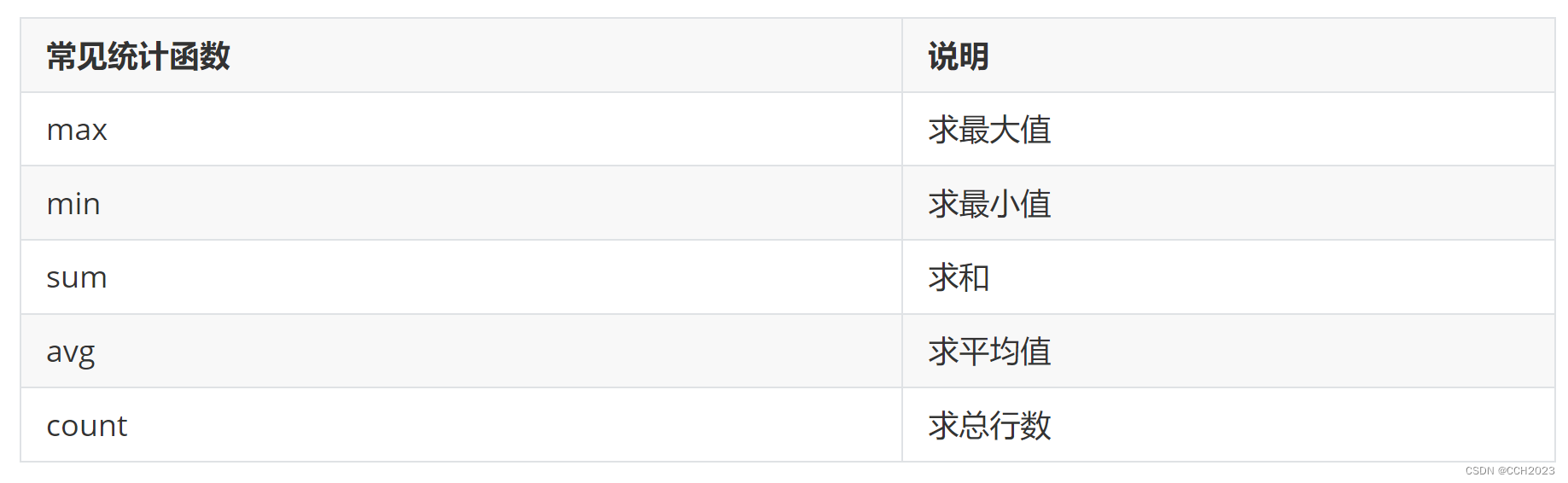
MySQL学习笔记13
DISTINCT数据去重: 案例:获取tb_student学生表学员年龄的分布情况。 mysql> select * from tb_student; ------------------------------------------------- | id | name | age | gender | address | --------------------------…...

怎么获取外网ip地址
在网络连接中,每个设备都被分配一个唯一的IP地址,用于标识和定位该设备。其中,内部或局域网IP地址是在局域网内使用的,而外网IP地址则是与公共互联网通信时所使用的地址。 获取外网IP地址对于许多人来说可能是一个常见的需求&…...
)
算法 只出现一次的两个数字-(哈希+异或)
牛客网: BM52 题目: 数组中仅2个数字出现1次,其余出现2次 思路: 出现2次的数字异或结果为0,另外两个不同的数字异或结果res不为0,异或结果的二进制位必与其中一个相同,求出二进制位为1的pos, 遍历数组,所有此位置为1…...
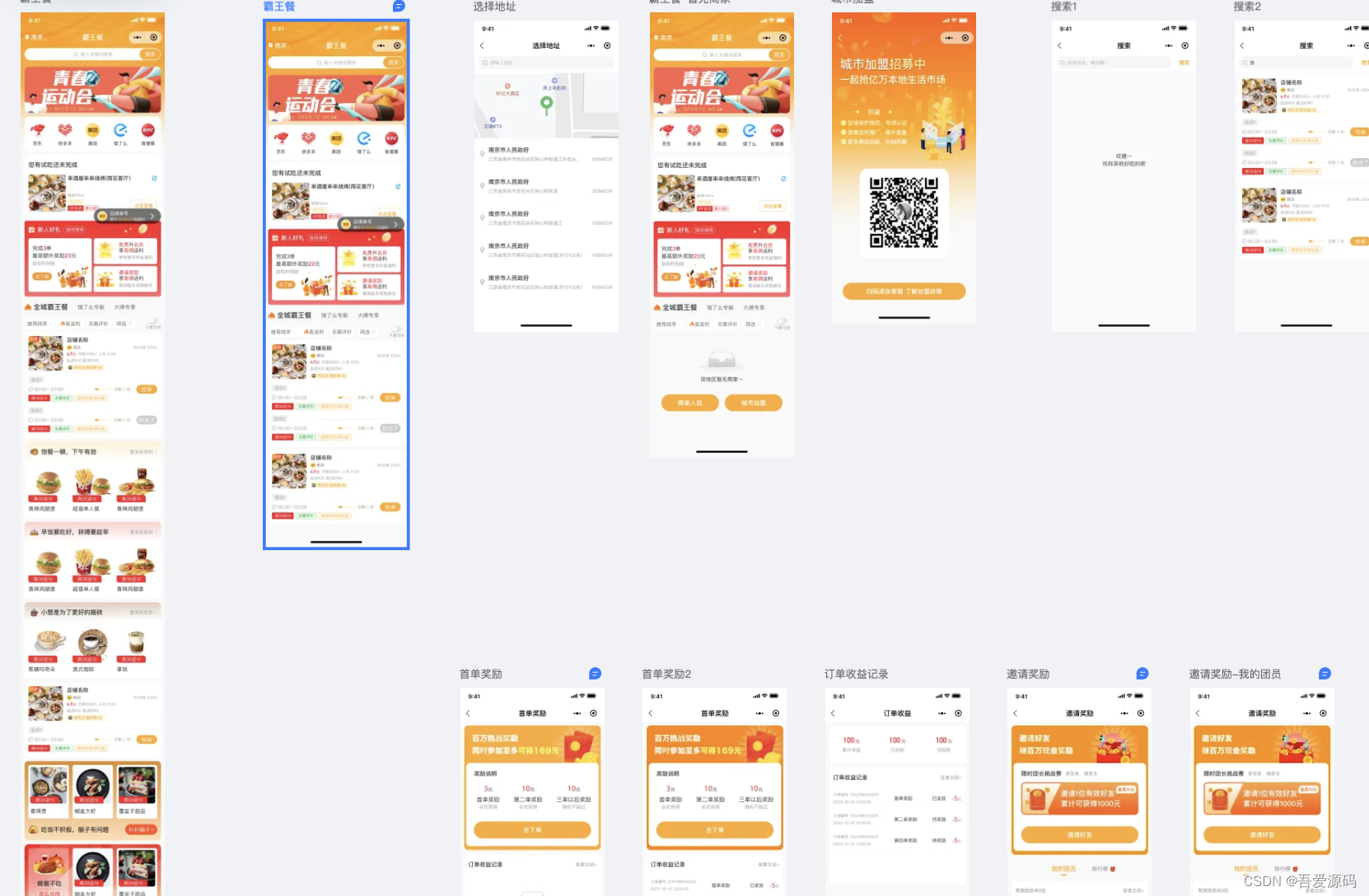
外卖霸王餐小程序、H5、公众号版外卖系统源码
最新外卖霸王餐小程序、H5、微信公众号版外卖系统源码、霸王餐美团、饿了么系统,粉丝裂变玩源码下载,外卖cps小程序项目,外卖红包cps带好友返利佣金分销系统程序、饿了么美团联盟源码,外卖cps带分销返利后端源码,基于L…...

amlogic 机顶盒关闭DLNA 后,手机还能搜到盒子
S905L3 带有投屏的功能,并通过 com.droidlogic.mediacenter.dlna.MediaCenterService 服务的启动和停止来开启和关闭DLNA功能,但是在测试中发现机顶盒关闭DLNA后,手机还能搜索到盒子。我在复测中发现关闭后有时很难很久搜索到盒子,…...

@Autowire、@Recourse用啥?
在使用IDEA写Spring相关的项目的时候,在字段上使用Autowired注解时,总是会有一个波浪线提示:Field injection is not recommended. 这是为啥呢?今天就来一探究竟。 众所周知,在Spring里面有三种可选的注入方式…...

[linux] 过滤警告⚠️
如果你在Python脚本中输出和执行脚本文件时想要过滤掉警告信息,可以尝试以下方法: 使用warnings模块:导入warnings模块并设置warnings.filterwarnings("ignore"),这将会忽略所有的警告信息。在需要过滤警告的部分之前添…...

Linux必备操作系统命令大全
一、基础命令 pwd 命令 pwd命令用于显示当前所在的工作目录的全路径名称。该命令无需任何参数,只需在终端窗口中输入 pwd 命令即可使用。 cd 命令 cd命令用于更改当前工作目录。该命令需要一个参数:目标目录名称。例如,若要进入 Document…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
