2023 ICPC 网络赛 第一场(补题:F)
7题罚时879, 队排235,校排79。
除了I题dp没注意空间限制第一发没有用滚动数组MLE,以及G题启发式合并脑抽用set当容器T一发,以及K没注意是平方的期望白wa4发这些应当避免的失误外,基本满意。剩下的题基本都是当时写不出的了,在这里补一发F的题解。
本题解学自:知乎-CurryWOE
F. Alice and Bob(博弈 + 计数)
很妙的一个博弈思维题,并没有多难的算法,只是利用了题目的性质与博弈的基本思想,以及巧妙的计数方法,但实际比赛中还是很难想到的,银牌题中上的难度。
题意
给定大小为 n n n 的数组 a a a,Alice先手,两人轮流走步,每次可以选择两个数 a i , a j a_i, a_j ai,aj,将其任意改变(只能变为整数),设改变后为 a i 2 , a j 2 a_{i_2},a_{j_2} ai2,aj2,要求改变后满足 a i + a j = a i 2 + a j 2 a_i+a_j = a_{i_2}+a_{j_2} ai+aj=ai2+aj2,且 ∣ a i − a j ∣ < ∣ a i 2 − a j 2 ∣ |a_i-a_j|<|a_{i_2}-a_{j_2}| ∣ai−aj∣<∣ai2−aj2∣. 最后不能走步的人输。
为了帮助Alice胜利,你可以选择保留任意 3 3 3 个数,移除其他数,问有多少方案使得Alice必胜。
思路
以上规则翻译过来就是,每次选的两个数必须使得两者差距变小,这样我们发现答案与数的大小无关,只与数的相对大小有关。于是我们可以分情况讨论什么样的三元组使得Alice必胜或必败。
设三元组为 ( x , y , z ) ( x ≤ y ≤ z ) (x, y, z)(x\leq y\leq z) (x,y,z)(x≤y≤z). 因为只与相对大小有关,可以通过平移转换为 ( 0 , x , x + y ) (0, x, x + y) (0,x,x+y),并且若 x > y x > y x>y 可以对称转换一下,使得 x < y x < y x<y 例如: ( 0 , 3 , 5 ) → ( − 5 , − 3 , 0 ) → ( 0 , 2 , 5 ) (0,3,5)\rightarrow(-5,-3,0)\rightarrow(0,2,5) (0,3,5)→(−5,−3,0)→(0,2,5).
接下来要用到博弈的思想:
1.所有终止状态都为必败态。
2.只要能转移到必败态的状态就是必胜态。
3.只能转移到必胜态的状态就是必败态。
分情况讨论
-
x > 0 , y > 0 x > 0,y>0 x>0,y>0,三元组为 ( 0 , x , x + y ) (0, x, x + y) (0,x,x+y)
我们考虑该三元组的下一个状态,有两种可能即 ( y , x , x ) (y, x, x) (y,x,x) 或者 ( x + k , x , y − k ) (x + k, x, y - k) (x+k,x,y−k). 再考虑状态 ( y , x , x ) (y,x,x) (y,x,x) 的后继,只能为 ( x + k , x , y − k ) (x + k, x, y - k) (x+k,x,y−k).
若 ( y , x , x ) (y,x,x) (y,x,x) 为必败态,则当前状态可以转移到该必败态,当前为必胜态。
若 ( y , x , x ) (y,x,x) (y,x,x) 为必胜态,由于其只有一个后继,说明该后继一定为必败态,而当前状态又能转移到该必败态,当前状态同样必胜。
综上, ( 0 , x , x + y ) (0, x, x + y) (0,x,x+y) 一定为必胜态。 -
x > 0 , y = 0 / x = 0 , y > 0 x > 0,y = 0/x = 0,y>0 x>0,y=0/x=0,y>0,三元组为 ( 0 , 0 , x ) (0, 0, x) (0,0,x)( x > 0 x>0 x>0)
为何 ( 0 , x , x ) (0,x,x) (0,x,x) 同样为该状态,还是考虑平移与对称变化: ( 0 , x , x ) → ( − x , 0 , 0 ) → ( x , 0 , 0 ) (0,x,x)\rightarrow (-x,0,0)\rightarrow(x,0,0) (0,x,x)→(−x,0,0)→(x,0,0). 而 y > 0 y>0 y>0 的情况因为只是一个变量名,将其名称与 x x x 交换即可。
(1)若 x x x 为奇数当前状态的后继最多为 ( 0 , ⌊ x 2 ⌋ , ⌈ x 2 ⌉ ) (0,\lfloor\frac x2\rfloor,\lceil\frac x2\rceil) (0,⌊2x⌋,⌈2x⌉) 即可以表示为 ( 0 , x , y ) ( x < y ) (0,x,y)(x<y) (0,x,y)(x<y). 而情况1 已经证明了该后继状态为必胜态,则当前状态为必败态。
(2)若 x x x 为偶数当前状态后继若选择变为 ( 0 , x , y ) (0,x,y) (0,x,y),则必败。考虑另一种情况即将 x x x 一分为二变为 ( 0 , x 2 , x 2 ) (0,\frac x2,\frac x2) (0,2x,2x),此时我们发现又一次变为了情况2,说明这是一个递归的过程,而答案只与 x x x 包含的 2 2 2 的幂次有关。
综上归纳整理有:若 x x x 包含的 2 2 2 的幂次为偶数先手必败,否则先手必胜。
合并起来看:
- 三元组 ( x , y , z ) , ( x < y < z ) (x,y,z),(x<y<z) (x,y,z),(x<y<z),必胜。
- 三元组 ( x , y , z ) , ( x = y / y = z ) (x,y,z),(x=y/y=z) (x,y,z),(x=y/y=z),若 ( z − x ) (z - x) (z−x) 包含的 2 2 2 的幂次为偶数必败,否则必胜。
- 三元组 ( x , y , z ) , ( x = y = z ) (x,y,z),(x=y=z) (x,y,z),(x=y=z),必败。
现在我们考虑如何计数,直接求必胜态数量不好求,我们考虑容斥求出必败态数量再用总数减去。情况3的必败态数量很好求,我们只需要考虑情况2的。
遍历所有数,设当前数为 x x x,那么我们只需要求 ( p , x , x ) ( x > p ) (p,x,x)(x>p) (p,x,x)(x>p) 和 ( x , x , z ) ( z > x ) (x,x,z)(z>x) (x,x,z)(z>x) 三元组中满足 x − p x - p x−p 和 z − x z - x z−x 包含的 2 2 2 的幂次为偶数的个数即可,可以考虑用01字典树来维护。
2 2 2 的幂次的奇偶只与数末尾 0 0 0 的个数的奇偶有关,而二进制减法中 x − y = z x - y = z x−y=z, z z z 末尾的第一个 1 1 1 出现在 x , y x,y x,y 从末尾开始第一个数字不同的数位,我们倒序将数的数位插入字典树,查询数目后就是简单的组合数学问题了。
时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),对于 n ≤ 5 e 5 , ∑ n ≤ 3 e 6 n\leq5e5,\sum n\leq3e6 n≤5e5,∑n≤3e6 的数据范围还是很轻松能通过的。
具体实现见代码,有详细注释。
代码
/*
1. 三元组 (x,y,z),(x<y<z),必胜。
2. 三元组 (x,y,z),(x=y/y=z),若 (z - x) 包含的 2 的幂次为偶数必败,否则必胜。
3. 三元组 (x,y,z),(x=y=z),必败。
*/
#include <bits/stdc++.h>
using namespace std;#define ll long long
const int N = 5e5 + 10;ll a[N];
int son[N * 62][2], cnt[N * 62], tot;
void clear(int p){if(son[p][0]) clear(son[p][0]);if(son[p][1]) clear(son[p][1]);son[p][0] = son[p][1] = cnt[p] = 0;
}void insert(ll x){int p = 0;for(int i = 0; i <= 60; i ++){ // 倒序插入int u = x >> i & 1;if(!son[p][u]) son[p][u] = ++ tot;p = son[p][u];cnt[p] ++;}
}ll search(ll x, int idx, int p, int ode){ // 查询的数x, 当前数位,字典树地址, 奇偶性ll sum = 0;int u = x >> idx & 1;if(son[p][!u] && !ode){ // 下一位数不同,且当前0的个数为偶数,即为差包含偶数次2的幂次,加入答案sum += cnt[son[p][!u]];}if(son[p][u]) sum += search(x, idx + 1, son[p][u], ode ^ 1); // 继续搜索return sum;
}ll C2(ll sum){ // C(sum, 2)return sum * (sum - 1) / 2LL;
}
ll C3(ll sum){ // C(sum, 3)return sum * (sum - 1) * (sum - 2) / 6LL;
}void solve(){int n;cin >> n;clear(0); tot = 0;for(int i = 1; i <= n; i ++){cin >> a[i];insert(a[i]);}sort(a + 1, a + 1 + n);ll ans = C3(n); // 总方案数for(int i = 1, r = 1; i <= n; i ++){while(r + 1 <= n && a[r + 1] == a[i]) r ++;ans -= C2(r - i + 1) * search(a[i], 0, 0, 0); // 情况2的必败数ans -= C3(r - i + 1); // 情况3的必败数i = r;}cout << ans;
}int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);int t;cin >> t;for(int i = 1; i <= t; i ++){solve();if(i != t) cout << "\n";}return 0;
}
相关文章:
)
2023 ICPC 网络赛 第一场(补题:F)
7题罚时879, 队排235,校排79。 除了I题dp没注意空间限制第一发没有用滚动数组MLE,以及G题启发式合并脑抽用set当容器T一发,以及K没注意是平方的期望白wa4发这些应当避免的失误外,基本满意。剩下的题基本都是当时写不出…...

MySQL慢查询优化、日志收集定位排查、慢查询sql分析
MySQL慢查询日志收集、定位,慢查询分析、排查。 一 MySQL慢查询定位 1. 确定是否已开启慢查询日志 查看慢查询日志是否已经被开启: SHOW VARIABLES LIKE slow_query_log; 如果返回值是OFF,你需要开启它。 2. 开启慢查询日志 你可以临时在运…...

HZOJ-266:表达式计算
题目描述 给出一个表达式,其中运算符仅包含 ,-,*,/,^ 要求求出表达式的最终值。 数据可能会出现括号情况,还有可能出现多余括号情况,忽略多余括号,正常计算即可; 数据保证不会出现大于 max long int 的数据࿱…...

JavaScript学习小结
变量声明:使用var关键字,变量没有类型,但值有类型(弱类型语言) 数据类型: ①number ②string(单引号,双引号都可以表示字符串) ③boolean ④Object类型 ⑤undefine…...
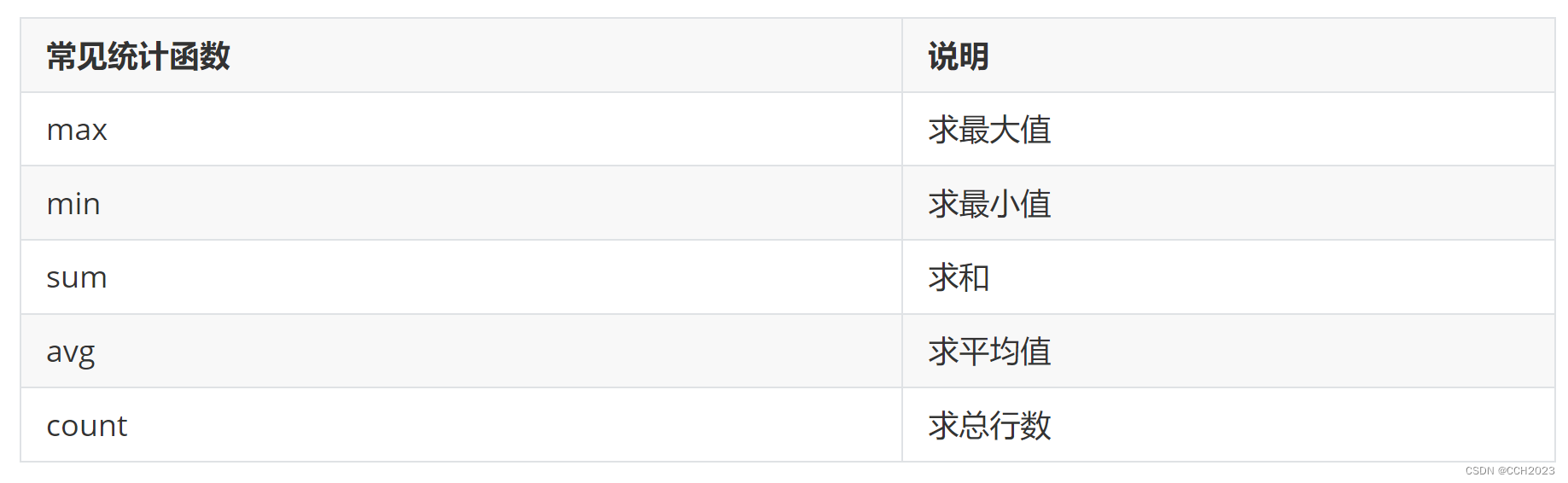
MySQL学习笔记13
DISTINCT数据去重: 案例:获取tb_student学生表学员年龄的分布情况。 mysql> select * from tb_student; ------------------------------------------------- | id | name | age | gender | address | --------------------------…...

怎么获取外网ip地址
在网络连接中,每个设备都被分配一个唯一的IP地址,用于标识和定位该设备。其中,内部或局域网IP地址是在局域网内使用的,而外网IP地址则是与公共互联网通信时所使用的地址。 获取外网IP地址对于许多人来说可能是一个常见的需求&…...
)
算法 只出现一次的两个数字-(哈希+异或)
牛客网: BM52 题目: 数组中仅2个数字出现1次,其余出现2次 思路: 出现2次的数字异或结果为0,另外两个不同的数字异或结果res不为0,异或结果的二进制位必与其中一个相同,求出二进制位为1的pos, 遍历数组,所有此位置为1…...
外卖霸王餐小程序、H5、公众号版外卖系统源码
最新外卖霸王餐小程序、H5、微信公众号版外卖系统源码、霸王餐美团、饿了么系统,粉丝裂变玩源码下载,外卖cps小程序项目,外卖红包cps带好友返利佣金分销系统程序、饿了么美团联盟源码,外卖cps带分销返利后端源码,基于L…...

amlogic 机顶盒关闭DLNA 后,手机还能搜到盒子
S905L3 带有投屏的功能,并通过 com.droidlogic.mediacenter.dlna.MediaCenterService 服务的启动和停止来开启和关闭DLNA功能,但是在测试中发现机顶盒关闭DLNA后,手机还能搜索到盒子。我在复测中发现关闭后有时很难很久搜索到盒子,…...

@Autowire、@Recourse用啥?
在使用IDEA写Spring相关的项目的时候,在字段上使用Autowired注解时,总是会有一个波浪线提示:Field injection is not recommended. 这是为啥呢?今天就来一探究竟。 众所周知,在Spring里面有三种可选的注入方式…...

[linux] 过滤警告⚠️
如果你在Python脚本中输出和执行脚本文件时想要过滤掉警告信息,可以尝试以下方法: 使用warnings模块:导入warnings模块并设置warnings.filterwarnings("ignore"),这将会忽略所有的警告信息。在需要过滤警告的部分之前添…...

Linux必备操作系统命令大全
一、基础命令 pwd 命令 pwd命令用于显示当前所在的工作目录的全路径名称。该命令无需任何参数,只需在终端窗口中输入 pwd 命令即可使用。 cd 命令 cd命令用于更改当前工作目录。该命令需要一个参数:目标目录名称。例如,若要进入 Document…...

【rtp】VideoTimingExtension 扩展的解析和写入
VideoTimingExtension 扩展有13个字节,并非都是字符串类型 class VideoTimingExtension {public:using value_type = VideoSendTiming;static constexpr RTPExtensionType kId = kRtpExtensionVideoTiming;static constexpr uint8_t kValueSizeBytes = 13...

网络安全CTF比赛有哪些事?——《CTF那些事儿》告诉你
目录 前言 一、内容简介 二、读者对象 三、专家推荐 四、全书目录 前言 CTF比赛是快速提升网络安全实战技能的重要途径,已成为各个行业选拔网络安全人才的通用方法。但是,本书作者在从事CTF培训的过程中,发现存在几个突出的问题࿱…...
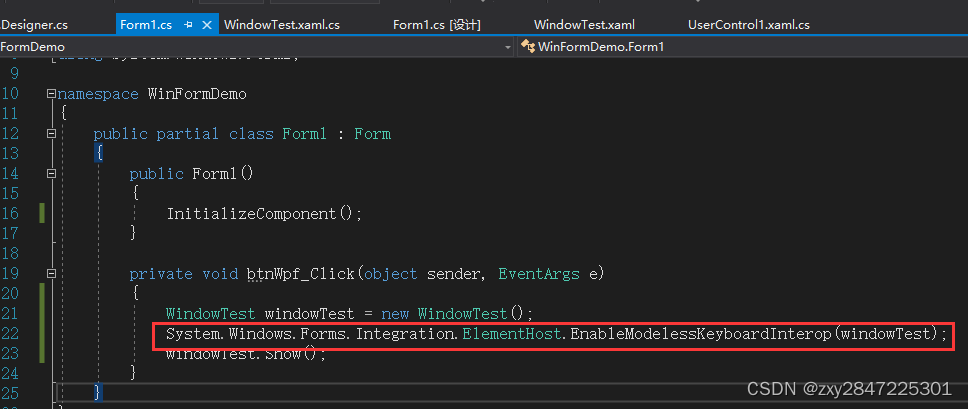
Winform直接与Wpf交互
Winform项目中,可以直接使用wpf中的自定义控件和窗体 测试环境: vistual studio 2017 window 10 一 winform直接使用wpf的自定义控件 步骤如下: 1 新建winfrom项目,名为WinFormDemo,默认有一个名为Form1的窗体…...
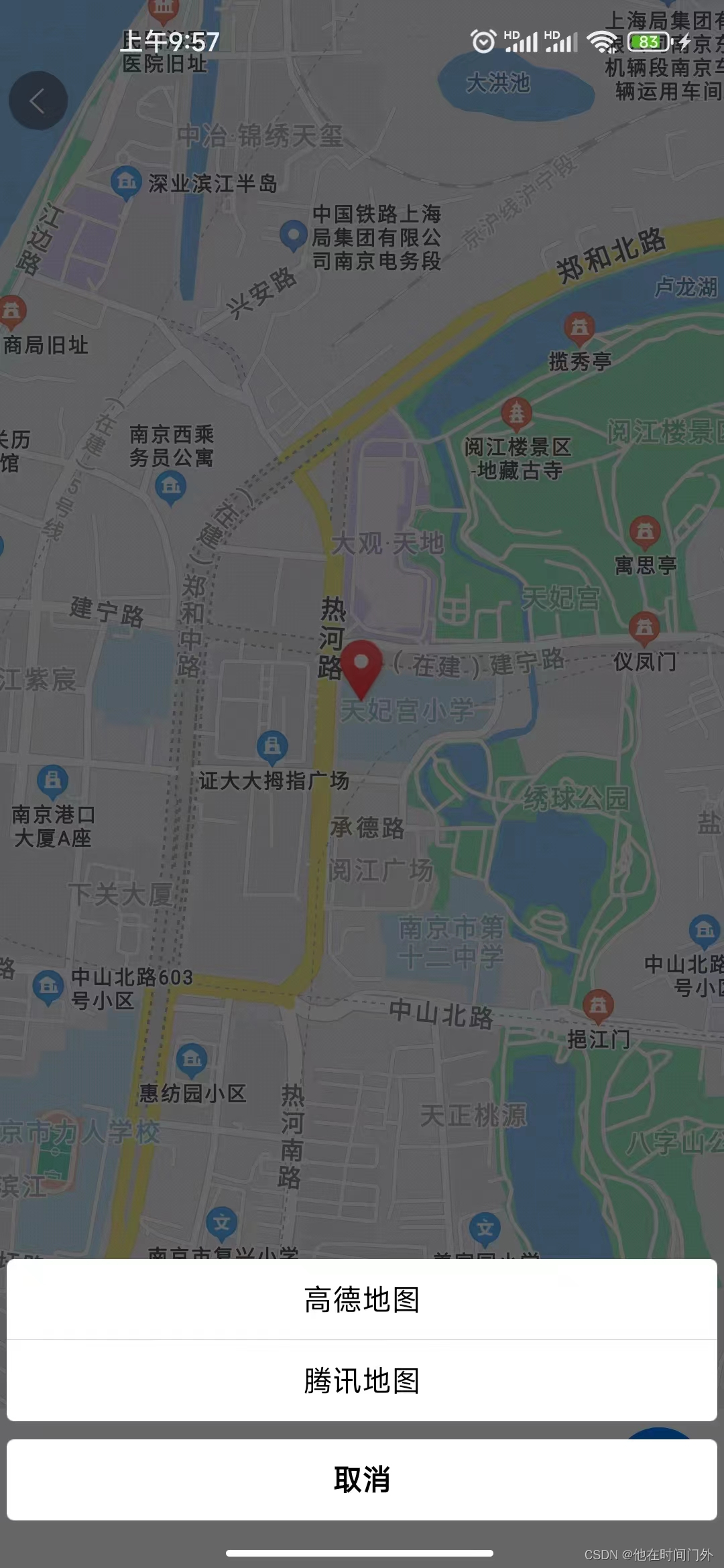
Uni-app 调用微信地图导航功能【有图】
前言 我们在使用uni-app时,有时候会遇到需要开发地图和导航的功能,这些方法其实微信小程序的API已经帮我们封装好了 详见:微信小程序开发文档 接下来我们就演示如何用uni-app来使用他们 使用 <template><view><button type…...

Golang slice 通过growslice调用nextslicecap计算扩容
先来看一段代码 code: e : []int64{1, 2, 3}fmt.Println("cap of e before:", cap(e))e append(e, 4, 5, 6, 7)fmt.Println("cap of e after:", cap(e))output:cap of e before: 3 cap of e after: 8 为什么容量是8? append了的4个元素&…...
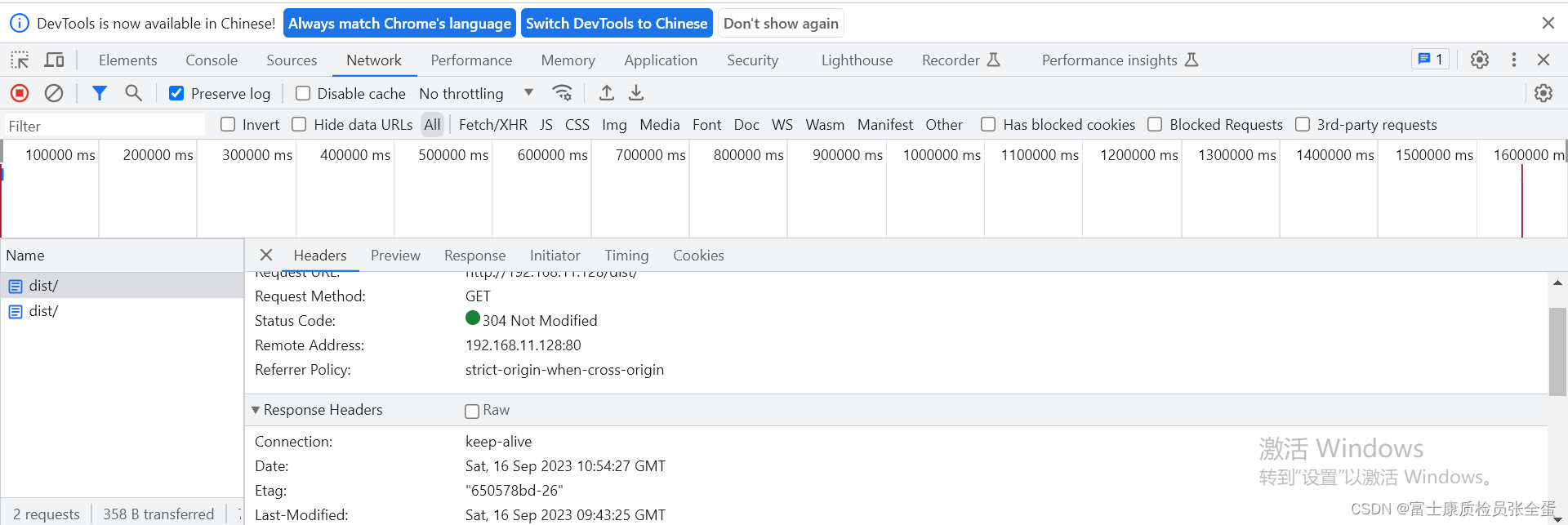
HTTP 协商缓存 Last-Modified,If-Modified-Since
浏览器第一次跟服务器请求一个资源,服务器在返回这个资源的同时,在respone header加上Last-Modified属性(表示这个资源在服务器上的最后修改时间): ----------------------------------------------------------------…...
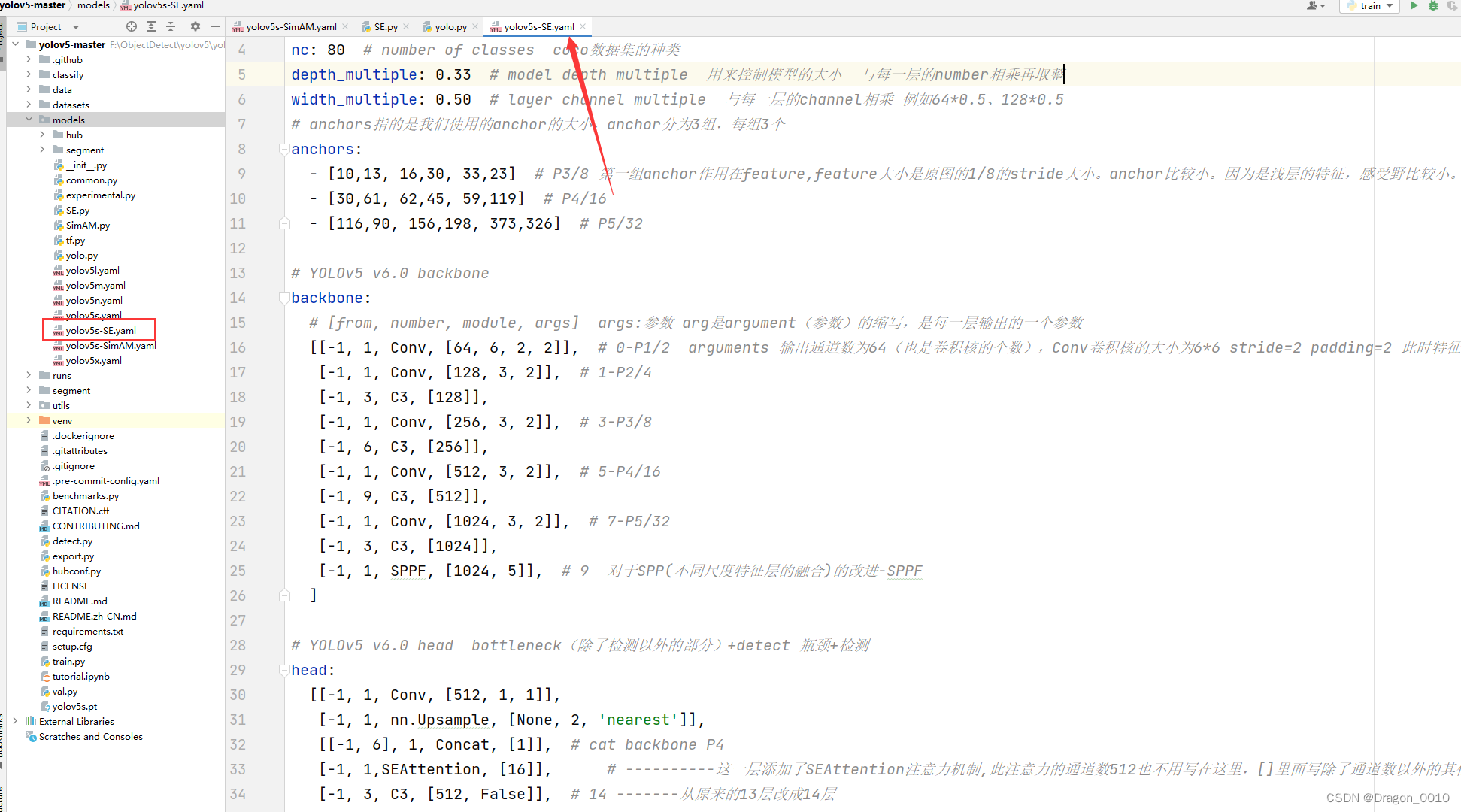
零基础教程:Yolov5模型改进-添加13种注意力机制
1.准备工作 先给出13种注意力机制的下载地址: https://github.com/z1069614715/objectdetection_script 2.加入注意力机制 1.以添加SimAM注意力机制为例(不需要接收通道数的注意力机制) 1.在models文件下新建py文件,取名叫Sim…...

vue截取地址参数
const getQueryValueFn () >{// 获取当前页面的URLconst currentURL window.location.href;//创建一个URL对象来解析当前URL。URL对象提供了方便的属性和方法来处理URL的各个部分const url new URL(currentURL);// 使用URLSearchParams获取查询参数const queryParams ne…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
