密度估计公式
- 极大似然估计:
y = p ( x 1 , x 2 , x 3 , . . . , x n ) = 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 y = p(x_1,x_2,x_3,...,x_n) = \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1-\mu)^2}{2\sigma ^ 2}} \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_2-\mu)^2}{2\sigma ^ 2}}...\frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_n-\mu)^2}{2\sigma ^ 2}} y=p(x1,x2,x3,...,xn)=2πσ1e−2σ2(x1−μ)22πσ1e−2σ2(x2−μ)2...2πσ1e−2σ2(xn−μ)2
l n y = l n p ( x 1 , x 2 , x 3 , . . . , x n ) = l n ( 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 ) = − n l n ( 2 π σ ) − ∑ i = 1 n ( x i − μ ) 2 2 σ 2 lny = ln p(x_1,x_2,x_3,...,x_n) =ln( \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1-\mu)^2}{2\sigma ^ 2}} \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_2-\mu)^2}{2\sigma ^ 2}}...\frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_n-\mu)^2}{2\sigma ^ 2}} ) =\\ -nln(\sqrt{2 \pi} \sigma ) - \sum_{i=1}^{n}\frac{(x_i-\mu)^2}{2\sigma ^ 2} lny=lnp(x1,x2,x3,...,xn)=ln(2πσ1e−2σ2(x1−μ)22πσ1e−2σ2(x2−μ)2...2πσ1e−2σ2(xn−μ)2)=−nln(2πσ)−i=1∑n2σ2(xi−μ)2
要求y的极限值(将 μ 和 σ \mu 和 \sigma μ和σ视为变量,x视为常量),只需要对上述等式两边对x求导并令导数为0:
∂ ln y ∂ μ = ∑ i = 1 n ( x i − μ ) σ 2 = 0 \frac{\partial \ln y}{\partial \mu} = \sum_{i=1}^{n} \frac{(x_i - \mu)}{\sigma ^ 2} = 0 ∂μ∂lny=i=1∑nσ2(xi−μ)=0
即: μ = 1 n ∑ i = 1 n ( x i ) \mu = \frac{1}{n}\sum_{i=1}^{n} (x_i) μ=n1∑i=1n(xi)
∂ ln y ∂ σ = − n 1 σ + ∑ i = 1 n ( x i − μ ) 2 σ 3 = 0 \frac{\partial \ln y}{\partial \sigma} =-n\frac{1}{\sigma} +\sum_{i=1}^{n} \frac{(x_i - \mu)^2}{\sigma ^ 3} = 0 ∂σ∂lny=−nσ1+i=1∑nσ3(xi−μ)2=0
即: σ 2 = ∑ i = 1 n ( x i − μ ) 2 n \sigma^2 = \sum_{i=1}^{n} \frac{(x_i - \mu)^2}{n} σ2=∑i=1nn(xi−μ)2
- 先验估计:
y = p ( x 1 , x 2 , x 3 , . . . , x n ; θ 0 ) = 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 1 2 π σ 0 e − ( μ 0 − μ ) 2 2 σ 0 2 y = p(x_1,x_2,x_3,...,x_n;\theta_0) = \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1-\mu)^2}{2\sigma ^ 2}} \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_2-\mu)^2}{2\sigma ^ 2}}...\frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_n-\mu)^2}{2\sigma ^ 2}} \frac{1}{\sqrt{2\pi} \sigma_0} e ^{-\frac{(\mu_0-\mu)^2}{2\sigma_0 ^ 2}} y=p(x1,x2,x3,...,xn;θ0)=2πσ1e−2σ2(x1−μ)22πσ1e−2σ2(x2−μ)2...2πσ1e−2σ2(xn−μ)22πσ01e−2σ02(μ0−μ)2
l n y = l n p ( x 1 , x 2 , x 3 , . . . , x n ; θ 0 ) = l n ( 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 1 2 π σ 0 e − ( μ 0 − μ ) 2 2 σ 0 2 ) = − n l n ( 2 π σ ) − ∑ i = 1 n ( x i − μ ) 2 2 σ 2 − l n ( 2 π σ 0 ) − ( μ 0 − μ ) 2 2 σ 0 2 lny = ln p(x_1,x_2,x_3,...,x_n;\theta_0) =ln( \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1-\mu)^2}{2\sigma ^ 2}} \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_2-\mu)^2}{2\sigma ^ 2}}...\frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_n-\mu)^2}{2\sigma ^ 2}} \frac{1}{\sqrt{2\pi} \sigma_0}e ^{-\frac{(\mu_0-\mu)^2}{2\sigma_0 ^ 2}} )=\\ -nln(\sqrt{2 \pi} \sigma ) - \sum_{i=1}^{n}\frac{(x_i-\mu)^2}{2\sigma ^ 2} -ln(\sqrt{2 \pi} \sigma _0) -\frac{(\mu_0-\mu)^2}{2\sigma_0 ^ 2} lny=lnp(x1,x2,x3,...,xn;θ0)=ln(2πσ1e−2σ2(x1−μ)22πσ1e−2σ2(x2−μ)2...2πσ1e−2σ2(xn−μ)22πσ01e−2σ02(μ0−μ)2)=−nln(2πσ)−i=1∑n2σ2(xi−μ)2−ln(2πσ0)−2σ02(μ0−μ)2
要求y的极限值(将 μ 和 σ \mu 和 \sigma μ和σ视为变量,x视为常量),只需要对上述等式两边对x求导并令导数为0:
∂ ln y ∂ μ = ∑ i = 1 n ( x i − μ ) σ 2 + ( μ 0 − μ ) σ 0 2 = 0 \frac{\partial \ln y}{\partial \mu} = \sum_{i=1}^{n} \frac{(x_i - \mu)}{\sigma ^ 2} +\frac{(\mu_0- \mu)}{\sigma_0 ^ 2} = 0 ∂μ∂lny=i=1∑nσ2(xi−μ)+σ02(μ0−μ)=0
即:
∂ ln y ∂ μ = 1 σ 2 ∑ i = 1 n x i − n μ σ 2 + μ 0 σ 0 2 − μ σ 0 2 = 0 \frac{\partial \ln y}{\partial \mu} = \frac{1}{\sigma^2}\sum_{i=1}^{n} x_i - \frac{n\mu}{\sigma^2}+ \frac{\mu_0}{\sigma_0 ^ 2} - \frac{\mu}{\sigma_0 ^ 2}= 0 ∂μ∂lny=σ21i=1∑nxi−σ2nμ+σ02μ0−σ02μ=0
1 σ 2 ∑ i = 1 n x i + μ 0 σ 0 2 = ( n σ 2 + 1 σ 0 2 ) μ \frac{1}{\sigma^2}\sum_{i=1}^{n} x_i + \frac{\mu_0}{\sigma_0 ^ 2} = ( \frac{n}{\sigma^2} +\frac{1}{\sigma_0 ^ 2} )\mu σ21i=1∑nxi+σ02μ0=(σ2n+σ021)μ
μ = 1 σ 2 ∑ i = 1 n x i + μ 0 σ 0 2 n σ 2 + 1 σ 0 2 \mu = \frac{ \frac{1}{\sigma^2}\sum_{i=1}^{n} x_i + \frac{\mu_0}{\sigma_0 ^ 2} }{\frac{n}{\sigma^2} +\frac{1}{\sigma_0 ^ 2} } μ=σ2n+σ021σ21∑i=1nxi+σ02μ0
这里要注意的是,贝叶斯估计在 θ 0 \theta_0 θ0处的先验概率的计算方式,此时要将 u 0 和 σ 0 当作先验参数 u_0和\sigma_0当作先验参数 u0和σ0当作先验参数
相关文章:

密度估计公式
极大似然估计: y p ( x 1 , x 2 , x 3 , . . . , x n ) 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 y p(x_1,x_2,x_3,...,x_n) \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1…...
)
2023 ICPC 网络赛 第一场(补题:F)
7题罚时879, 队排235,校排79。 除了I题dp没注意空间限制第一发没有用滚动数组MLE,以及G题启发式合并脑抽用set当容器T一发,以及K没注意是平方的期望白wa4发这些应当避免的失误外,基本满意。剩下的题基本都是当时写不出…...

MySQL慢查询优化、日志收集定位排查、慢查询sql分析
MySQL慢查询日志收集、定位,慢查询分析、排查。 一 MySQL慢查询定位 1. 确定是否已开启慢查询日志 查看慢查询日志是否已经被开启: SHOW VARIABLES LIKE slow_query_log; 如果返回值是OFF,你需要开启它。 2. 开启慢查询日志 你可以临时在运…...

HZOJ-266:表达式计算
题目描述 给出一个表达式,其中运算符仅包含 ,-,*,/,^ 要求求出表达式的最终值。 数据可能会出现括号情况,还有可能出现多余括号情况,忽略多余括号,正常计算即可; 数据保证不会出现大于 max long int 的数据࿱…...

JavaScript学习小结
变量声明:使用var关键字,变量没有类型,但值有类型(弱类型语言) 数据类型: ①number ②string(单引号,双引号都可以表示字符串) ③boolean ④Object类型 ⑤undefine…...
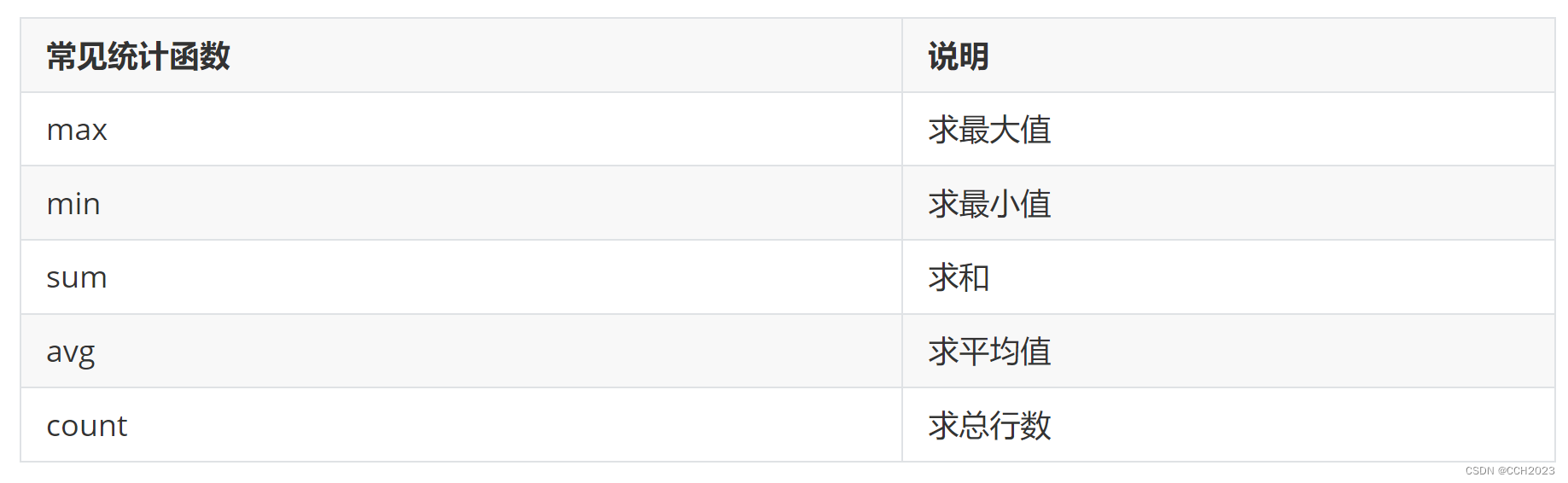
MySQL学习笔记13
DISTINCT数据去重: 案例:获取tb_student学生表学员年龄的分布情况。 mysql> select * from tb_student; ------------------------------------------------- | id | name | age | gender | address | --------------------------…...

怎么获取外网ip地址
在网络连接中,每个设备都被分配一个唯一的IP地址,用于标识和定位该设备。其中,内部或局域网IP地址是在局域网内使用的,而外网IP地址则是与公共互联网通信时所使用的地址。 获取外网IP地址对于许多人来说可能是一个常见的需求&…...
)
算法 只出现一次的两个数字-(哈希+异或)
牛客网: BM52 题目: 数组中仅2个数字出现1次,其余出现2次 思路: 出现2次的数字异或结果为0,另外两个不同的数字异或结果res不为0,异或结果的二进制位必与其中一个相同,求出二进制位为1的pos, 遍历数组,所有此位置为1…...
外卖霸王餐小程序、H5、公众号版外卖系统源码
最新外卖霸王餐小程序、H5、微信公众号版外卖系统源码、霸王餐美团、饿了么系统,粉丝裂变玩源码下载,外卖cps小程序项目,外卖红包cps带好友返利佣金分销系统程序、饿了么美团联盟源码,外卖cps带分销返利后端源码,基于L…...

amlogic 机顶盒关闭DLNA 后,手机还能搜到盒子
S905L3 带有投屏的功能,并通过 com.droidlogic.mediacenter.dlna.MediaCenterService 服务的启动和停止来开启和关闭DLNA功能,但是在测试中发现机顶盒关闭DLNA后,手机还能搜索到盒子。我在复测中发现关闭后有时很难很久搜索到盒子,…...

@Autowire、@Recourse用啥?
在使用IDEA写Spring相关的项目的时候,在字段上使用Autowired注解时,总是会有一个波浪线提示:Field injection is not recommended. 这是为啥呢?今天就来一探究竟。 众所周知,在Spring里面有三种可选的注入方式…...

[linux] 过滤警告⚠️
如果你在Python脚本中输出和执行脚本文件时想要过滤掉警告信息,可以尝试以下方法: 使用warnings模块:导入warnings模块并设置warnings.filterwarnings("ignore"),这将会忽略所有的警告信息。在需要过滤警告的部分之前添…...

Linux必备操作系统命令大全
一、基础命令 pwd 命令 pwd命令用于显示当前所在的工作目录的全路径名称。该命令无需任何参数,只需在终端窗口中输入 pwd 命令即可使用。 cd 命令 cd命令用于更改当前工作目录。该命令需要一个参数:目标目录名称。例如,若要进入 Document…...

【rtp】VideoTimingExtension 扩展的解析和写入
VideoTimingExtension 扩展有13个字节,并非都是字符串类型 class VideoTimingExtension {public:using value_type = VideoSendTiming;static constexpr RTPExtensionType kId = kRtpExtensionVideoTiming;static constexpr uint8_t kValueSizeBytes = 13...

网络安全CTF比赛有哪些事?——《CTF那些事儿》告诉你
目录 前言 一、内容简介 二、读者对象 三、专家推荐 四、全书目录 前言 CTF比赛是快速提升网络安全实战技能的重要途径,已成为各个行业选拔网络安全人才的通用方法。但是,本书作者在从事CTF培训的过程中,发现存在几个突出的问题࿱…...
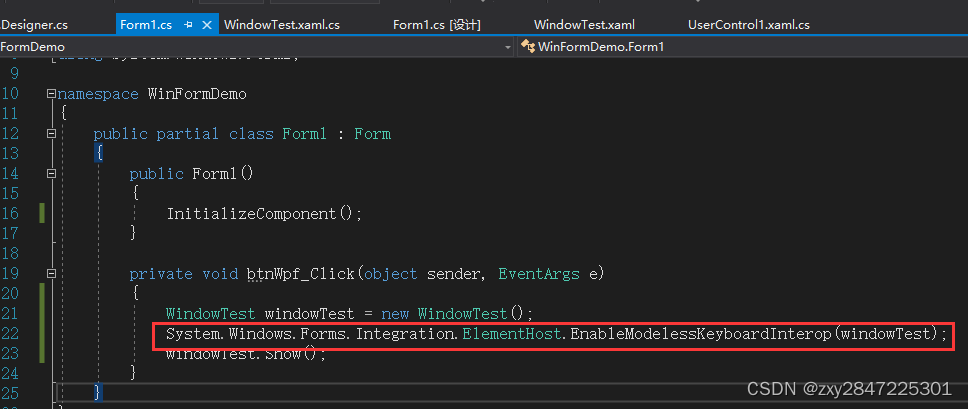
Winform直接与Wpf交互
Winform项目中,可以直接使用wpf中的自定义控件和窗体 测试环境: vistual studio 2017 window 10 一 winform直接使用wpf的自定义控件 步骤如下: 1 新建winfrom项目,名为WinFormDemo,默认有一个名为Form1的窗体…...
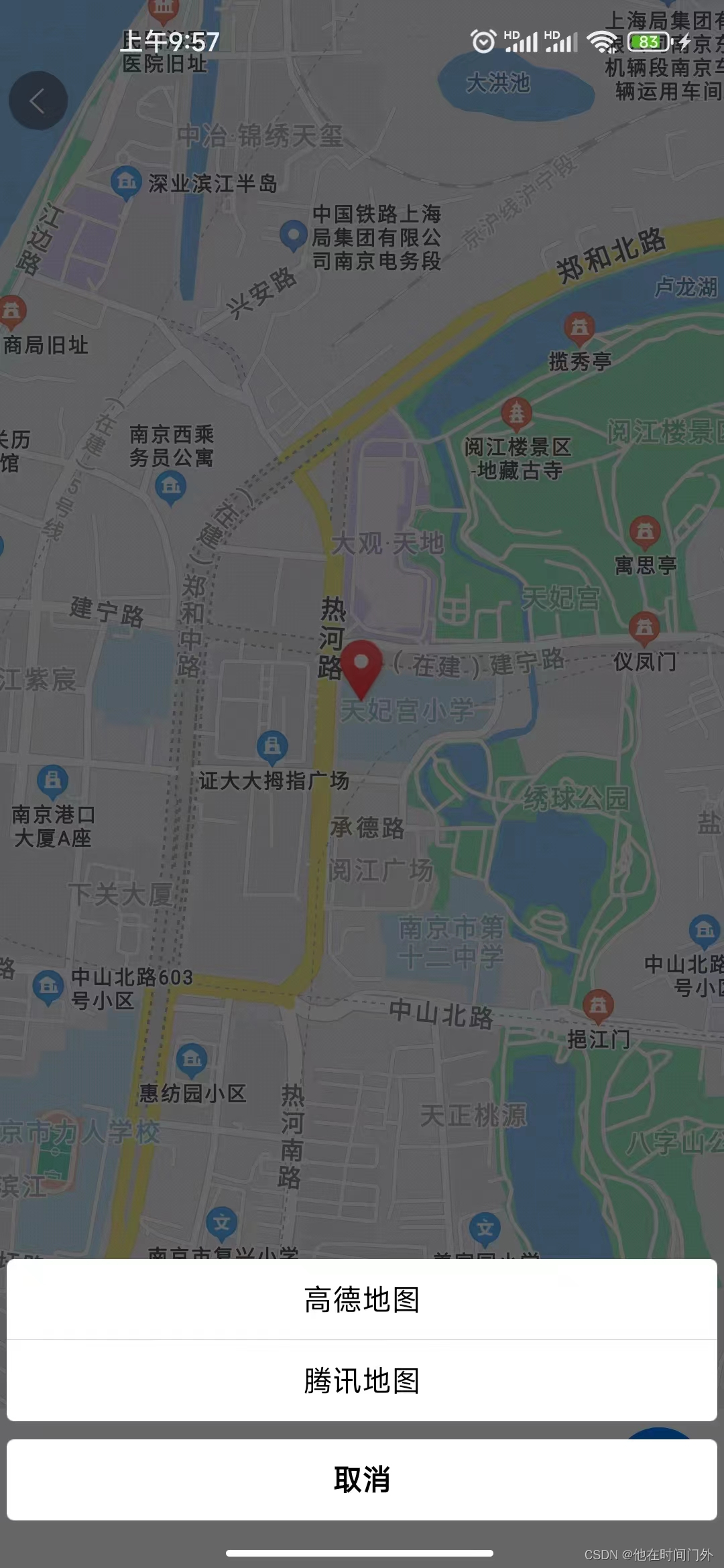
Uni-app 调用微信地图导航功能【有图】
前言 我们在使用uni-app时,有时候会遇到需要开发地图和导航的功能,这些方法其实微信小程序的API已经帮我们封装好了 详见:微信小程序开发文档 接下来我们就演示如何用uni-app来使用他们 使用 <template><view><button type…...

Golang slice 通过growslice调用nextslicecap计算扩容
先来看一段代码 code: e : []int64{1, 2, 3}fmt.Println("cap of e before:", cap(e))e append(e, 4, 5, 6, 7)fmt.Println("cap of e after:", cap(e))output:cap of e before: 3 cap of e after: 8 为什么容量是8? append了的4个元素&…...
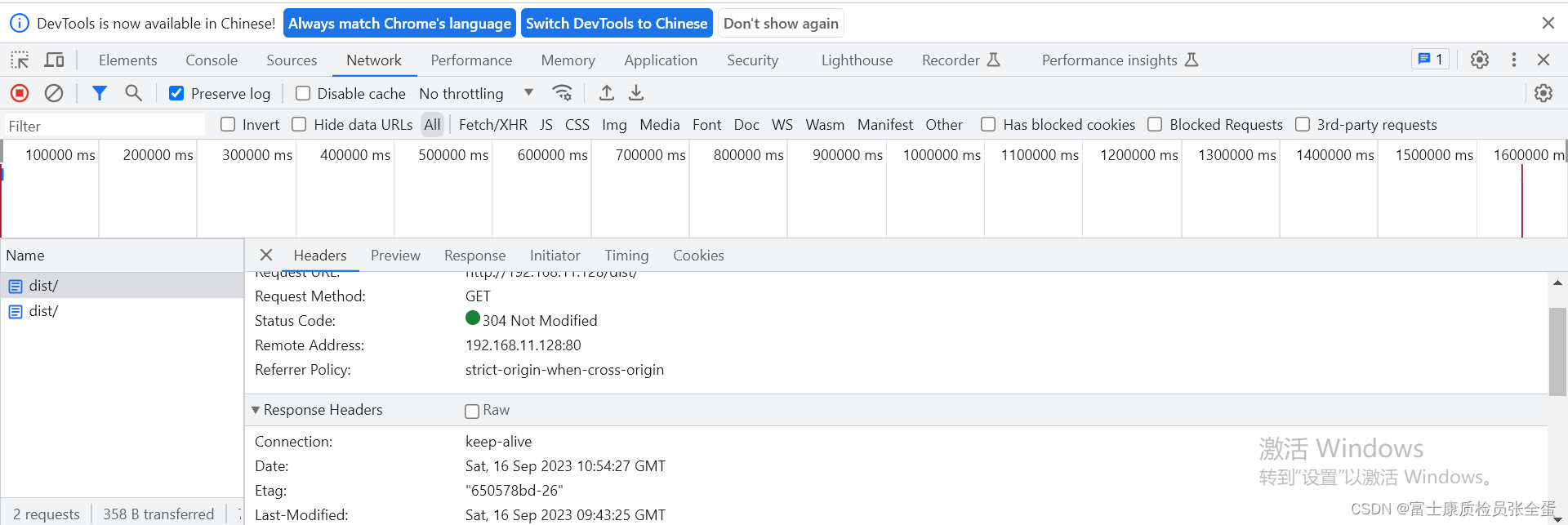
HTTP 协商缓存 Last-Modified,If-Modified-Since
浏览器第一次跟服务器请求一个资源,服务器在返回这个资源的同时,在respone header加上Last-Modified属性(表示这个资源在服务器上的最后修改时间): ----------------------------------------------------------------…...
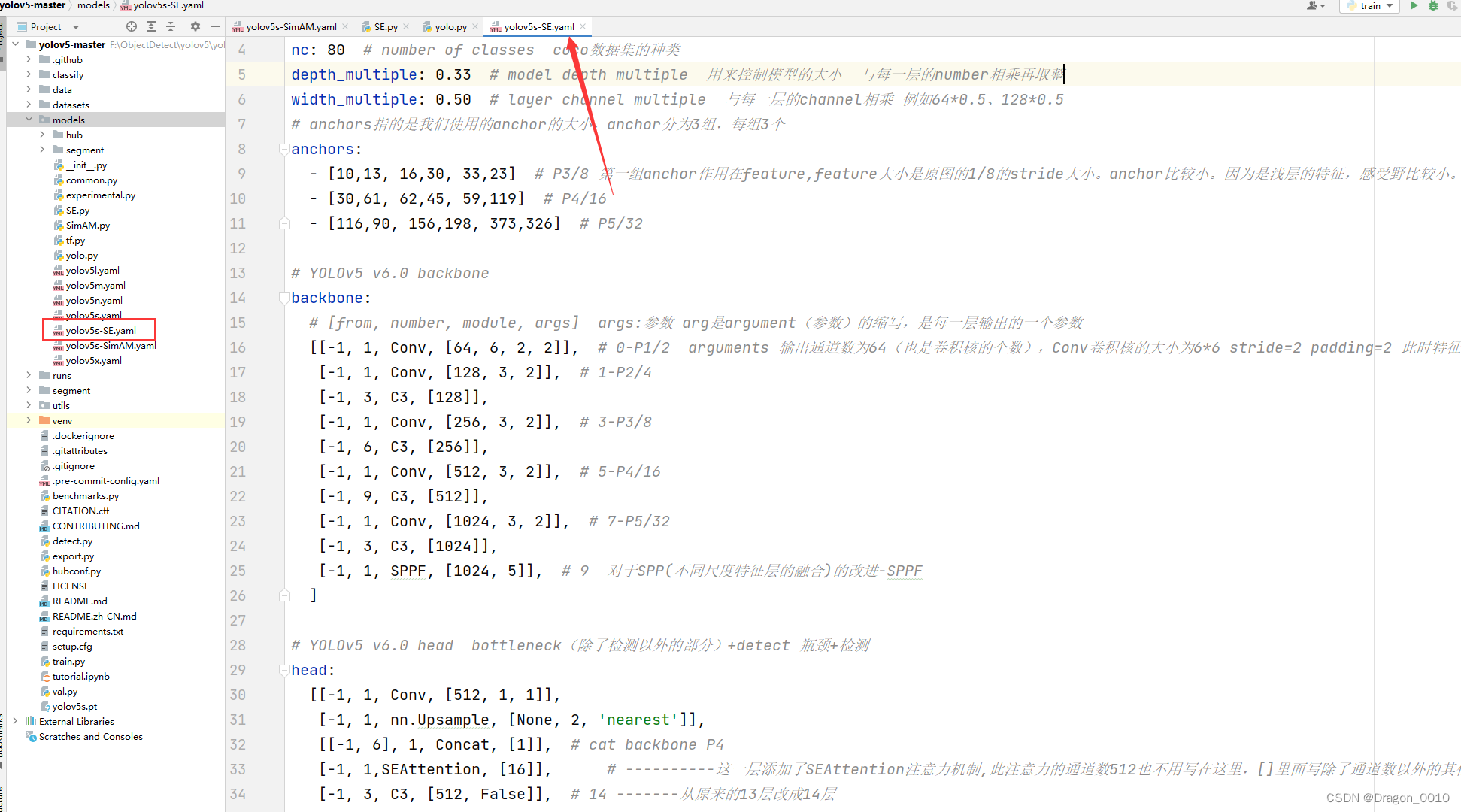
零基础教程:Yolov5模型改进-添加13种注意力机制
1.准备工作 先给出13种注意力机制的下载地址: https://github.com/z1069614715/objectdetection_script 2.加入注意力机制 1.以添加SimAM注意力机制为例(不需要接收通道数的注意力机制) 1.在models文件下新建py文件,取名叫Sim…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
