数学公式测试
MVP变换
MVP变换用来描述视图变换的任务,即将虚拟世界中的三维物体映射(变换)到二维坐标中。
MVP变换分为三步:
- 模型变换(model tranformation):将模型空间转换到世界空间(找个好的地方,把所有人集合在一起,摆个pose)
- 摄像机变换(view tranformation):将世界空间转换到观察空间(找到一个放相机的位置,往某一个角度去看)
- 投影变换(projection tranformation):将观察空间转换到裁剪空间(茄子!)
在这之后,还有一个#视口变换
视图变换(View)
视图变换的目的是变换Camera位置到原点,上方为Y,观察方向为-Z,即
M v i e w = R v i e w T v i e w = [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t y t z t 0 x − g y g z − g 0 0 0 0 1 ] [ 1 0 0 − x e 0 1 0 − y c 0 0 1 − z c 0 0 0 1 ] \begin{align} M_{view}&=R_{view}T_{view}\\ &=\begin{bmatrix} x_{\hat{g}\times\hat{t}}& y_{\hat{g}\times\hat{t}}& z_{\hat{g}\times\hat{t}}& 0\\ x_{t}& y_{t}& z_{t}& 0\\ x_{-g}& y_{g}& z_{-g}& 0\\ 0& 0& 0& 1 \end{bmatrix} \begin{bmatrix}1& 0& 0& -x_{e}\\ 0& 1& 0& -y_{c}\\ 0& 0& 1& -z_{c}\\ 0& 0& 0& 1\end{bmatrix} \end{align} Mview=RviewTview= xg^×t^xtx−g0yg^×t^ytyg0zg^×t^ztz−g00001 100001000010−xe−yc−zc1

定义Camera:
- Camera位置 e ⃗ \vec{e} e
- 观察方向 g ^ \hat{g} g^
- 视点上方向 t ^ \hat{t} t^
规定:
- Camera的y轴正方向向上,z轴方向是 − x ⃗ × y ⃗ -\vec{x}\times \vec{y} −x×y(右手系)
- 对物体进行运动,摄像机会跟随着一起运动保持相对位置不变。
变换Camera位置到原点,上方为Y,观察方向为-Z:
- 把 e ⃗ \vec{e} e移动到标准位置: T v i e w = [ 1 0 0 − x e 0 1 0 − y c 0 0 1 − z c 0 0 0 1 ] T_{view}=\begin{bmatrix}1& 0& 0& -x_{e}\\ 0& 1& 0& -y_{c}\\ 0& 0& 1& -z_{c}\\ 0& 0& 0& 1\end{bmatrix} Tview= 100001000010−xe−yc−zc1 (因为朝原点移动,所以为负)
- 旋转 g ^ \hat{g} g^到-Z , t ⃗ \vec{t} t到Y, g ^ × t ⃗ \hat{g}\times\vec{t} g^×t到X: R v i e w = [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t y t z t 0 x − g y g z − g 0 0 0 0 1 ] R_{view}=\begin{bmatrix}x_{\hat{g}\times\hat{t}}& y_{\hat{g}\times\hat{t}}& z_{\hat{g}\times\hat{t}}& 0\\ x_{t}& y_{t}& z_{t}& 0\\x_{-g}& y_{g}& z_{-g}& 0\\ 0& 0& 0& 1\end{bmatrix} Rview= xg^×t^xtx−g0yg^×t^ytyg0zg^×t^ztz−g00001
推导:这个过程是旋转X到 g ^ × t ^ \hat{g}\times\hat{t} g^×t^,Y到 t ^ \hat{t} t^,Z到 − g ^ -\hat{g} −g^的逆过程。所以 R v i e w R_{view} Rview是这个逆过程的逆矩阵(正交矩阵的逆是转置矩阵):
模型变换和视图变换经常被一起叫作模型视图变换(ModelView Translation)
投影变换(Projection)
投影变换分为两种:
- 正交投影变换:透视线平行
- 透视投影变换:透视线相交,近大远小

正交投影
M o r t h o = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + L 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] \begin{align} M_{ortho}&=\begin{bmatrix}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{bmatrix} \begin{bmatrix}1& 0& 0& -\frac{r+L}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{bmatrix}\\\\ &=\begin{bmatrix}\frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& \frac{2}{n-f}& -\frac{n+f}{n-f}\\ 0& 0& 0& 1\end{bmatrix} \end{align} Mortho= r−l20000t−b20000n−f200001 100001000010−2r+L−2t+b−2n+f1 = r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1
正交投影的核心:用一个立方体框住物体的 [ l , r ] × [ b , t ] × [ f , n ] [l,r]\times[b,t]\times[f,n] [l,r]×[b,t]×[f,n],把这个立方体变换到标准正方体 [ − 1 , 1 ] 3 [-1,1]^{3} [−1,1]3中。
变换顺序:先移动(中点移动到原点),再缩放(基向量缩放比例为 2 长 / 宽 / 高 \frac{2}{长/宽/高} 长/宽/高2 )。

注意事项:
- 右手系:n>f
- OpenGl是左手系
透视投影
M p e r = M o r t h o M p e r s p → − o r t h o = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] = [ 2 n r − l 0 l + r l − r 0 0 2 n t − b b + t b − t 0 0 0 f + n n − f 2 f n f − n 0 0 1 0 ] \begin{align} M_{per}&=M_{ortho}M_{persp\rightarrow -ortho}\\\\ &=\begin{bmatrix}\frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& \frac{2}{n-f}& -\frac{n+f}{n-f}\\ 0& 0& 0& 1\end{bmatrix}\begin{bmatrix}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{bmatrix}\\\\ &=\begin{bmatrix}\frac{2n}{r-l}& 0&\frac{l+r}{l-r}& 0\\ 0& \frac{2n}{t-b}& \frac{b+t}{b-t}& 0\\ 0& 0& \frac{f+n}{n-f}& \frac{2fn}{f-n}\\ 0& 0& 1& 0\end{bmatrix} \end{align} Mper=MorthoMpersp→−ortho= r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1 n0000n0000n+f100−nf0 = r−l2n0000t−b2n00l−rl+rb−tb+tn−ff+n100f−n2fn0
透视投影的核心:用“远平面”和“近平面”框住物体,先把“远平面”向“近平面“挤压,然后做一次正交投影。
即透视投影分为两步:
- 将透视投影转化为正交投影
- 将正交投影转换到正则立方体

研究挤压:
规定:
- 挤压过程中,近平面和远平面的z值不发生变换(中间要发生变化)
- 挤压过程中,远平面中心原点 ( x , y ) T (x,y)^{T} (x,y)T不发生变化
挤压过程中的x,y变化的比例关系:

x同理。
y ′ = n z y , x ′ = n z x y' = \frac{n}{z}y,~~x'=\frac{n}{z}x y′=zny, x′=znx
用齐次坐标描述任一点的坐标变换:
[ x y z 1 ] → [ n x / z n y / z u n k n o w n 1 ] = [ n x n y z ⋅ u n k o w n z ] \begin{align} \begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}\rightarrow \begin{bmatrix} nx/z\\ ny/z\\ unknown\\ 1\end{bmatrix}=\begin{bmatrix}nx\\ ny\\ z\cdot unkown\\ z\end{bmatrix} \end{align} xyz1 → nx/zny/zunknown1 = nxnyz⋅unkownz
把这个变换用齐次坐标矩阵表示:
M ( 4 × 4 ) [ x y z 1 ] = = [ n x n y z ⋅ u n k o w n z ] M(4\times 4)\begin{bmatrix}x\\ y\\ z\\ 1\end{bmatrix}==\begin{bmatrix}nx\\ ny\\ z\cdot unkown\\ z\end{bmatrix} M(4×4) xyz1 == nxnyz⋅unkownz
根据矩阵乘法,可以写出M的大致形式:
M = [ n 0 0 0 0 n 0 0 ? ? ? ? 0 0 1 0 ] M=\begin{bmatrix}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{bmatrix} M= n0?00n?000?100?0
代入上面提到的两种点:
- 近平面或远平面上的任一点(令 u n k n o w n = n , z = n unknown=n,z=n unknown=n,z=n): M [ x y n 1 ] = [ n x n y n 2 n ] M\begin{bmatrix}x\\ y\\ n\\ 1\end{bmatrix}=\begin{bmatrix}nx\\ ny\\ n^{2}\\ n\end{bmatrix} M xyn1 = nxnyn2n 根据矩阵乘法行操作: M 第三行 [ x y n 1 ] = n 2 M第三行\begin{bmatrix}x\\ y\\ n\\ 1\end{bmatrix}=n^{2} M第三行 xyn1 =n2 因为不涉及旋转,所以第三行与x,y无关。 [ 0 0 A B ] [ x y n 1 ] = n 2 \begin{bmatrix}0& 0& A& B\end{bmatrix}\begin{bmatrix}x\\ y\\ n \\ 1\end{bmatrix}=n^{2} [00AB] xyn1 =n2 即: A n + B = n 2 An+B=n^{2} An+B=n2
- 远平面的原点(令 x = 0 , y = 0 , z = f x=0,y=0,z=f x=0,y=0,z=f): [ 0 0 f 1 ] → [ 0 0 f 2 f ] \begin{bmatrix}0\\ 0\\ f\\ 1\end{bmatrix} \rightarrow \begin{bmatrix}0\\ 0\\ f^{2}\\ f\end{bmatrix} 00f1 → 00f2f 同理可得: A f + B = f 2 Af+B=f^{2} Af+B=f2
综上所述,
A = n + f B = − n f A=n+f B=-nf A=n+fB=−nf
求得变换矩阵为:
M p e r s p → − o r t h o = [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] M_{persp\rightarrow -ortho}=\begin{bmatrix}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{bmatrix} Mpersp→−ortho= n0000n0000n+f100−nf0
得到透视投影矩阵为:
M p e r = M o r t h o M p e r s p → − o r t h o = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] = [ 2 n r − l 0 l + r l − r 0 0 2 n t − b b + t b − t 0 0 0 f + n n − f 2 f n f − n 0 0 1 0 ] \begin{align} M_{per}&=M_{ortho}M_{persp\rightarrow -ortho}\\\\ &=\begin{bmatrix}\frac{2}{r-l}& 0& 0& -\frac{r+l}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& \frac{2}{n-f}& -\frac{n+f}{n-f}\\ 0& 0& 0& 1\end{bmatrix}\begin{bmatrix}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{bmatrix}\\\\ &=\begin{bmatrix}\frac{2n}{r-l}& 0&\frac{l+r}{l-r}& 0\\ 0& \frac{2n}{t-b}& \frac{b+t}{b-t}& 0\\ 0& 0& \frac{f+n}{n-f}& \frac{2fn}{f-n}\\ 0& 0& 1& 0\end{bmatrix} \end{align} Mper=MorthoMpersp→−ortho= r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1 n0000n0000n+f100−nf0 = r−l2n0000t−b2n00l−rl+rb−tb+tn−ff+n100f−n2fn0
视口变换
视口变换
将处于标准平面映射到屏幕分辨率范围之内,即[-1,1]^2->[0,width]*[0,height], 其中width和height指屏幕分辨率大小
视锥
视锥表示看起来像顶部切割后平行于底部的金字塔的实体形状。这是透视摄像机可以看到和渲染的区域的形状。

定义视锥:
- 长宽比 Aspect
- 垂直的角度 FovY

利用视锥得到物体长宽高:

屏幕(Screen)
- 二维数组,数组元素为像素
- 典型的光栅成像设备
光栅(Raster)
- 德语中的屏幕
- 画在屏幕上
像素(Pixel <- PIcture element)
- 像素是一个颜色均匀的小正方形
- 颜色混合而成(红、绿、蓝)
屏幕空间
认为屏幕左下角是原点,向右是x,向上是y

规定:
- 像素坐标(Pixel’s indices)是(x, y)形式,x, y都是整数。
- 所有的像素都在(0, 0)到(width-1, height-1)之间
- 像素的中心:(x+0.5, y+0.5)
- 整个屏幕覆盖(0,0)to(width,height)
视口变换
要做的事情:
先不考虑z轴,把MVP后处于标准立方体 [ − 1 , 1 ] 3 [-1,1]^{3} [−1,1]3映射到屏幕上。即
[ − 1 , 1 ] 2 → [ 0 , w i d t h ] × [ 0 , h e i g h t ] [-1, 1]^{2}\rightarrow [0,width]\times [0,height] [−1,1]2→[0,width]×[0,height]
总结:把虚拟世界的任意可视物体转换到屏幕:
M = M v i e w M p e r M c a m M m o d e l M=M_{view}M_{per}M_{cam}M_{model} M=MviewMperMcamMmodel
相关文章:

数学公式测试
MVP变换 MVP变换用来描述视图变换的任务,即将虚拟世界中的三维物体映射(变换)到二维坐标中。 MVP变换分为三步: 模型变换(model tranformation):将模型空间转换到世界空间(找个好的地方,把所…...

机器学习——SVM(支持向量机)
0、前言: SVM应用:主要针对小样本数据进行学习、分类和回归(预测),能解决神经网络不能解决的过学习问题,有很好的泛化能力。(注意:SVM算法的数学原理涉及知识点比较多,所…...

【李沐深度学习笔记】基础优化方法
课程地址和说明 基础优化方法p2 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 基础优化方法 在讲具体的线性回归实现之前,要先讲一下基础的优化模型的方法 梯度下降 当模型没有显示解(…...

tmux 配置vim风格按键,支持gbk编码
vim修改~/.tmux.conf文件,没有则新增,添加如下内容。默认前缀更改为Ctrla。强烈建议更换Caps lock键位与Ctrl键位,用过的都说好,换过就回不来了。 unbind C-b set -g prefix C-a bind a send-prefixset -sg escape-time 1bind r …...
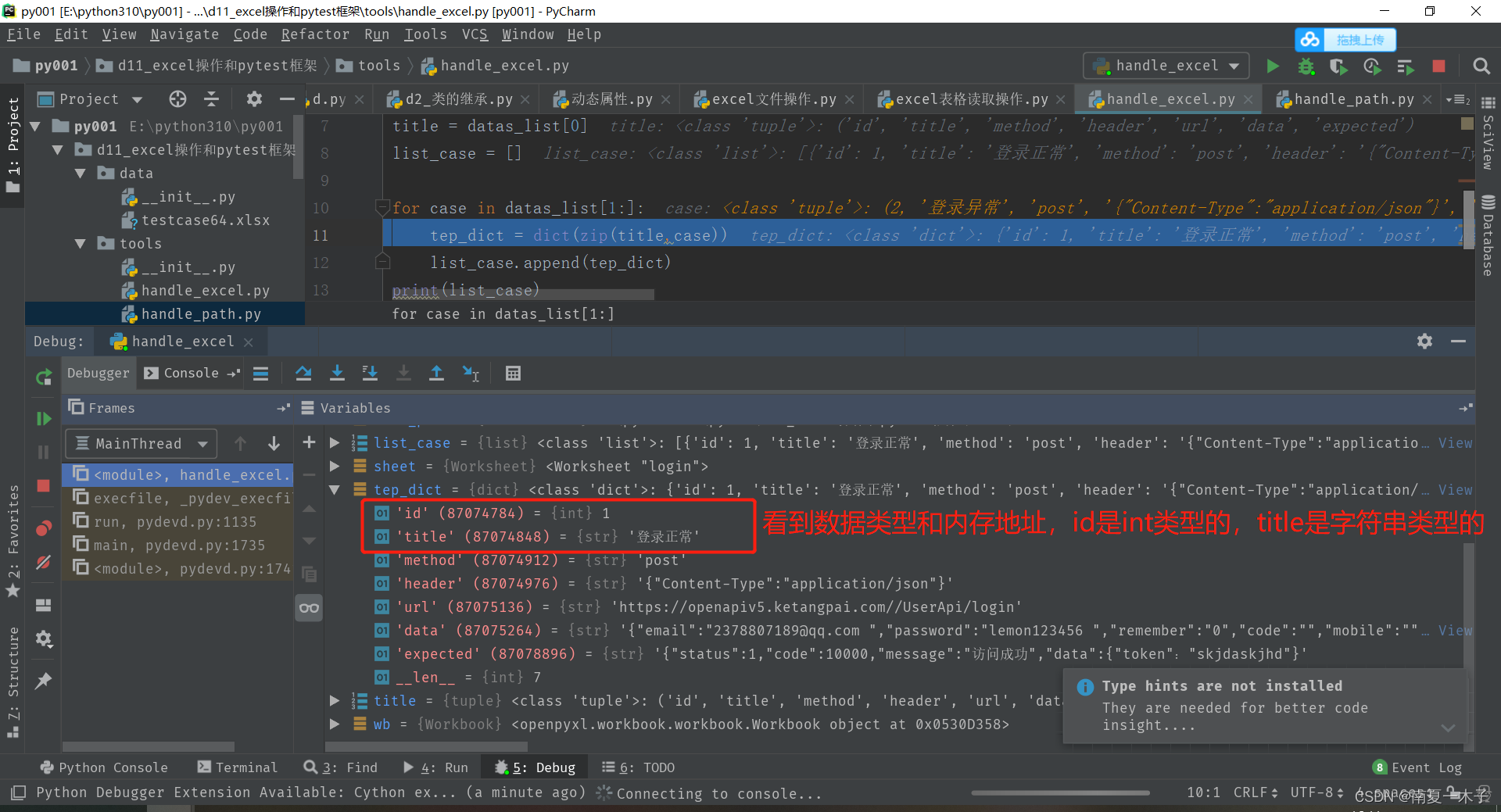
Python —— excel文件操作(超详细)
背景 很多公司还是用excel去管理测试用例的,所以为了减少重复繁琐的导出导出工作,学会如何用代码操作excel表格很实用~ 1、读取excel文件基本步骤 1、操作excel的一些库 1、xlrd:读取库,xlwt:写入,现在…...
什么是AI问答机器人?它的应用场景有哪些?
近年来,由于技术的进步和对个性化客户体验的需求不断增长,AI问答机器人也是获得了巨大的关注。AI问答机器人,也被称为AI聊天机器人,是一种旨在模拟人类对话并通过基于文本或语音的界面与用户交互的计算机程序。其能够自动执行各种…...

静态文件
静态文件 静态文件配置 - settings.py中 1,配置静态文件的访问路径【该配置默认存在】 通过哪个url地址找静态文件 STATIC URL‘/static/’ 说明 指定访问静态文件时是需要通过/static/xxx或http://127.0.0.1:8000/static/xxx [xxx表示具体的静态资源位置] 模…...

Centos7 自部署中间件开机启动,以及java应用开机启动方法
一、zookeeper cd /etc/rc.d/init.d/ touch zookeeper chmod x zookeeper vi zookeeper#以下为内容,自行修改 路径#!/bin/bash ##chkconfig:2345 10 90#description:service zookeeper #修改为自己的目录 export ZOO_LOG_DIR/data/apache-zookeeper-3.7.0/logs…...

密度估计公式
极大似然估计: y p ( x 1 , x 2 , x 3 , . . . , x n ) 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 y p(x_1,x_2,x_3,...,x_n) \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1…...
)
2023 ICPC 网络赛 第一场(补题:F)
7题罚时879, 队排235,校排79。 除了I题dp没注意空间限制第一发没有用滚动数组MLE,以及G题启发式合并脑抽用set当容器T一发,以及K没注意是平方的期望白wa4发这些应当避免的失误外,基本满意。剩下的题基本都是当时写不出…...

MySQL慢查询优化、日志收集定位排查、慢查询sql分析
MySQL慢查询日志收集、定位,慢查询分析、排查。 一 MySQL慢查询定位 1. 确定是否已开启慢查询日志 查看慢查询日志是否已经被开启: SHOW VARIABLES LIKE slow_query_log; 如果返回值是OFF,你需要开启它。 2. 开启慢查询日志 你可以临时在运…...

HZOJ-266:表达式计算
题目描述 给出一个表达式,其中运算符仅包含 ,-,*,/,^ 要求求出表达式的最终值。 数据可能会出现括号情况,还有可能出现多余括号情况,忽略多余括号,正常计算即可; 数据保证不会出现大于 max long int 的数据࿱…...

JavaScript学习小结
变量声明:使用var关键字,变量没有类型,但值有类型(弱类型语言) 数据类型: ①number ②string(单引号,双引号都可以表示字符串) ③boolean ④Object类型 ⑤undefine…...
MySQL学习笔记13
DISTINCT数据去重: 案例:获取tb_student学生表学员年龄的分布情况。 mysql> select * from tb_student; ------------------------------------------------- | id | name | age | gender | address | --------------------------…...

怎么获取外网ip地址
在网络连接中,每个设备都被分配一个唯一的IP地址,用于标识和定位该设备。其中,内部或局域网IP地址是在局域网内使用的,而外网IP地址则是与公共互联网通信时所使用的地址。 获取外网IP地址对于许多人来说可能是一个常见的需求&…...
)
算法 只出现一次的两个数字-(哈希+异或)
牛客网: BM52 题目: 数组中仅2个数字出现1次,其余出现2次 思路: 出现2次的数字异或结果为0,另外两个不同的数字异或结果res不为0,异或结果的二进制位必与其中一个相同,求出二进制位为1的pos, 遍历数组,所有此位置为1…...
外卖霸王餐小程序、H5、公众号版外卖系统源码
最新外卖霸王餐小程序、H5、微信公众号版外卖系统源码、霸王餐美团、饿了么系统,粉丝裂变玩源码下载,外卖cps小程序项目,外卖红包cps带好友返利佣金分销系统程序、饿了么美团联盟源码,外卖cps带分销返利后端源码,基于L…...

amlogic 机顶盒关闭DLNA 后,手机还能搜到盒子
S905L3 带有投屏的功能,并通过 com.droidlogic.mediacenter.dlna.MediaCenterService 服务的启动和停止来开启和关闭DLNA功能,但是在测试中发现机顶盒关闭DLNA后,手机还能搜索到盒子。我在复测中发现关闭后有时很难很久搜索到盒子,…...

@Autowire、@Recourse用啥?
在使用IDEA写Spring相关的项目的时候,在字段上使用Autowired注解时,总是会有一个波浪线提示:Field injection is not recommended. 这是为啥呢?今天就来一探究竟。 众所周知,在Spring里面有三种可选的注入方式…...

[linux] 过滤警告⚠️
如果你在Python脚本中输出和执行脚本文件时想要过滤掉警告信息,可以尝试以下方法: 使用warnings模块:导入warnings模块并设置warnings.filterwarnings("ignore"),这将会忽略所有的警告信息。在需要过滤警告的部分之前添…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...

