可转债实战与案例分析——成功的和失败的可转债投资案例、教训与经验分享
实战与案例分析——投资案例研究

一、成功的可转债投资案例
成功的可转债投资案例提供了有价值的经验教训,以下是一个典型的成功案例:
案例:投资者B的成功可转债投资
投资者B是一位懂得风险管理的投资者,他在某家知名科技公司发行的可转债上发现了投资机会。以下是他的投资故事:
投资背景:投资者B注意到该科技公司在技术创新和市场份额上有竞争优势,且财务稳健。公司发行了一只可转债,面值为1,000美元,利率为4%,转股价格较当前股价有一定溢价。
投资决策:投资者B认为,这只可转债有潜力在未来几年内获得股票增值。他购买了一笔可转债,投资金额为10,000美元。
长期持有:投资者B采用了长期持有策略,不追求短期快速利润。他计划持有该可转债至到期,并在需要时将其转换为公司的股票。
收益与教训:几年后,该科技公司的股价大幅上涨,达到了可转债的转股价格。投资者B选择将可转债转换为公司的股票,并获得了可观的股票增值。
这个成功案例强调了投资者B的理性决策、长期持有策略和对市场的深入分析。他成功地抓住了可转债的潜在增值机会,同时也控制了风险。

二、失败的可转债投资案例
失败的可转债投资案例也提供了宝贵的教训,以下是一个典型的失败案例:
案例:投资者C的可转债投资失败
投资者C是一位缺乏市场研究的投资者,他在某家新兴公司发行的可转债上投资,但未成功获利。以下是他的投资故事:
投资背景:投资者C听说了一家新兴科技公司,该公司声称拥有革命性的技术,并计划发行可转债。他决定迅速投资,未进行足够的研究和尽职调查。
投资决策:投资者C在可转债发行初期购买了大量可转债,投资金额高达20,000美元。
市场波动:不久后,该公司的股价开始下跌,由于公司的财务状况不佳和技术未能达到预期。
教训与经验分享:投资者C的失败案例强调了研究和尽职调查的重要性。他未能充分了解公司和市场条件,导致了投资亏损。此外,过度投资也增加了他的风险,因为他没有充分分散投资。

三、教训与经验分享
以上的成功和失败案例提供了以下几个重要教训和经验分享:
研究和尽职调查:在投资可转债之前,充分了解发行公司、行业和市场条件至关重要。投资者应该进行充分的研究和尽职调查,以便做出明智的决策。
长期持有策略:成功案例中的投资者采用了长期持有策略,不急于追求短期利润。这种策略可以帮助投资者充分利用可转债的潜在增值机会。
风险管理:投资者应该控制风险,避免过度投资,并确保投资组合多样化。这有助于降低潜在损失。
学习经验:失败案例强调了学习经验的重要性。投资者应该从失败中汲取教训,并不断改进他们的投资决策和策略。
无论成功还是失败,每个投资案例都提供了宝贵的经验和教训,帮助投资者不断提高他们的投资技能和智慧。在实际投资中,持续学习和反思是取得成功的关键。
相关文章:

可转债实战与案例分析——成功的和失败的可转债投资案例、教训与经验分享
实战与案例分析——投资案例研究 股票量化程序化自动交易接口 一、成功的可转债投资案例 成功的可转债投资案例提供了有价值的经验教训,以下是一个典型的成功案例: 案例:投资者B的成功可转债投资 投资者B是一位懂得风险管理的投资者&#…...
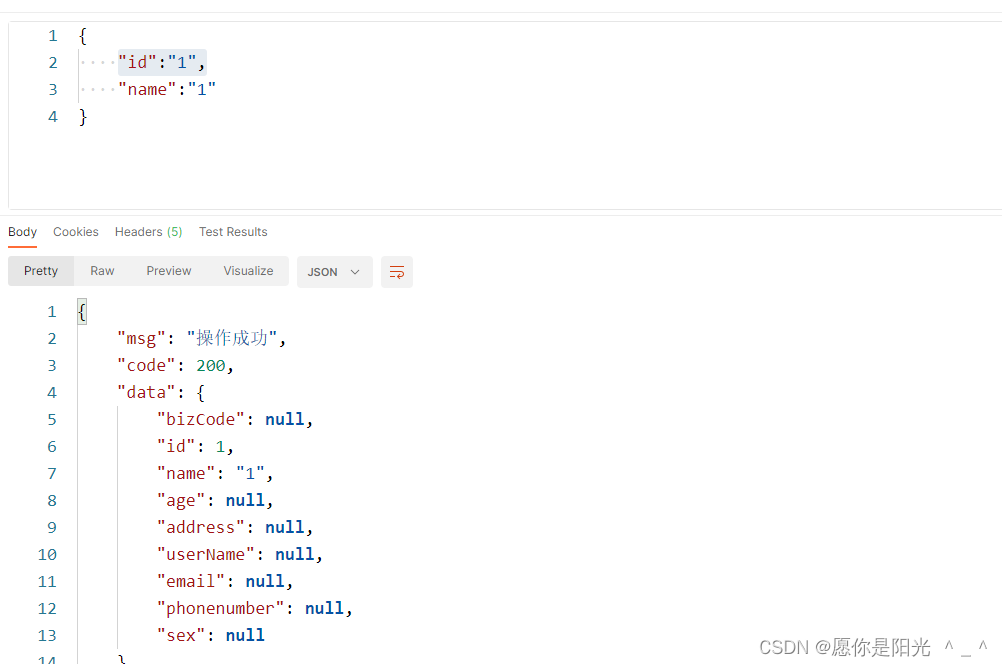
@NotNull注解不生效,全局异常处理
1.引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-validation</artifactId><version>3.1.2</version> </dependency> 2:实体类 实体类属性加上NotNull注解…...

【办公自动化】使用Python一键往Word文档的表格中填写数据(文末送书)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
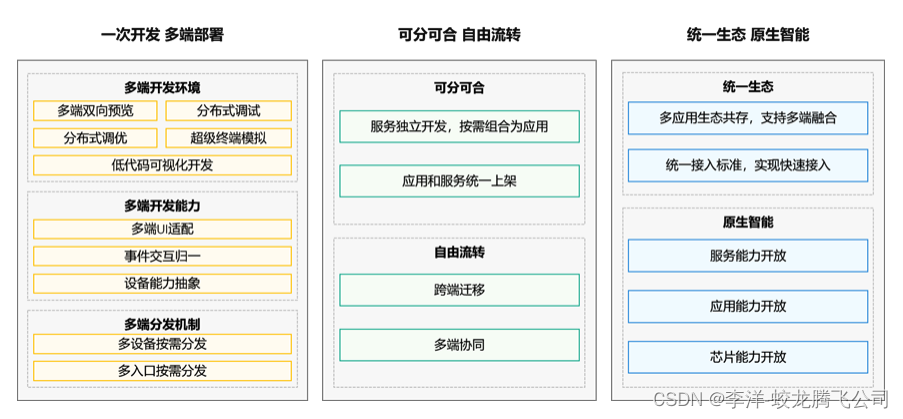
OpenHarmony应用核心技术理念与需求机遇简析
一、核心技术理念 图片来源:OpenHarmony官方网站 二、需求机遇简析 新的万物互联智能世界代表着新规则、新赛道、新切入点、新财富机会;各WEB网站、客户端( 苹果APP、安卓APK)、微信小程序等上的组织、企业、商户等;OpenHarmony既是一次机遇、同时又是一次大的挑战&…...

让Pegasus天马座开发板实现超声波测距
在完成《让Pegasus天马座开发板用上OLED屏》后,我觉得可以把超声波测距功能也在Pegasus天马座开发板上实现。于是在箱子里找到了,Grove - Ultrasonic Ranger 这一超声波测传感器。 官方地址: https://wiki.seeedstudio.com/Grove-Ultrasonic_Ranger 超声…...

C++11 多线程学习
C11学习 一、多线程 1、模板线程是以右值传递的 template <class Fn, class... Args> explicit thread(Fn&& fn, Args&&... args)则需要使用到std::ref和std::cref很好地解决了这个问题,std::ref 可以包装按引用传递的值。 std::cref 可以…...

数学公式测试
MVP变换 MVP变换用来描述视图变换的任务,即将虚拟世界中的三维物体映射(变换)到二维坐标中。 MVP变换分为三步: 模型变换(model tranformation):将模型空间转换到世界空间(找个好的地方,把所…...

机器学习——SVM(支持向量机)
0、前言: SVM应用:主要针对小样本数据进行学习、分类和回归(预测),能解决神经网络不能解决的过学习问题,有很好的泛化能力。(注意:SVM算法的数学原理涉及知识点比较多,所…...

【李沐深度学习笔记】基础优化方法
课程地址和说明 基础优化方法p2 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 基础优化方法 在讲具体的线性回归实现之前,要先讲一下基础的优化模型的方法 梯度下降 当模型没有显示解(…...

tmux 配置vim风格按键,支持gbk编码
vim修改~/.tmux.conf文件,没有则新增,添加如下内容。默认前缀更改为Ctrla。强烈建议更换Caps lock键位与Ctrl键位,用过的都说好,换过就回不来了。 unbind C-b set -g prefix C-a bind a send-prefixset -sg escape-time 1bind r …...
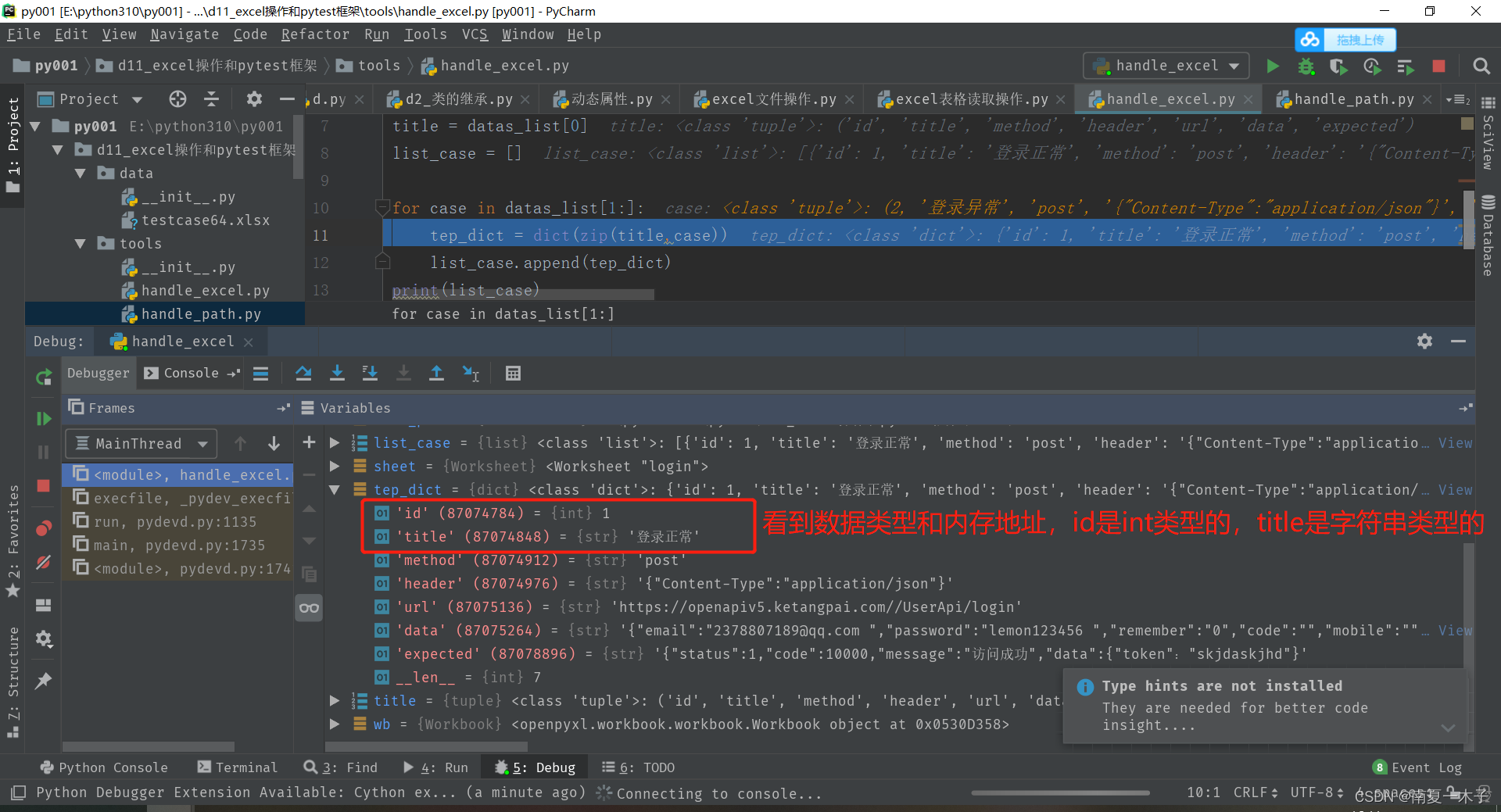
Python —— excel文件操作(超详细)
背景 很多公司还是用excel去管理测试用例的,所以为了减少重复繁琐的导出导出工作,学会如何用代码操作excel表格很实用~ 1、读取excel文件基本步骤 1、操作excel的一些库 1、xlrd:读取库,xlwt:写入,现在…...
什么是AI问答机器人?它的应用场景有哪些?
近年来,由于技术的进步和对个性化客户体验的需求不断增长,AI问答机器人也是获得了巨大的关注。AI问答机器人,也被称为AI聊天机器人,是一种旨在模拟人类对话并通过基于文本或语音的界面与用户交互的计算机程序。其能够自动执行各种…...

静态文件
静态文件 静态文件配置 - settings.py中 1,配置静态文件的访问路径【该配置默认存在】 通过哪个url地址找静态文件 STATIC URL‘/static/’ 说明 指定访问静态文件时是需要通过/static/xxx或http://127.0.0.1:8000/static/xxx [xxx表示具体的静态资源位置] 模…...

Centos7 自部署中间件开机启动,以及java应用开机启动方法
一、zookeeper cd /etc/rc.d/init.d/ touch zookeeper chmod x zookeeper vi zookeeper#以下为内容,自行修改 路径#!/bin/bash ##chkconfig:2345 10 90#description:service zookeeper #修改为自己的目录 export ZOO_LOG_DIR/data/apache-zookeeper-3.7.0/logs…...

密度估计公式
极大似然估计: y p ( x 1 , x 2 , x 3 , . . . , x n ) 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 y p(x_1,x_2,x_3,...,x_n) \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1…...
)
2023 ICPC 网络赛 第一场(补题:F)
7题罚时879, 队排235,校排79。 除了I题dp没注意空间限制第一发没有用滚动数组MLE,以及G题启发式合并脑抽用set当容器T一发,以及K没注意是平方的期望白wa4发这些应当避免的失误外,基本满意。剩下的题基本都是当时写不出…...

MySQL慢查询优化、日志收集定位排查、慢查询sql分析
MySQL慢查询日志收集、定位,慢查询分析、排查。 一 MySQL慢查询定位 1. 确定是否已开启慢查询日志 查看慢查询日志是否已经被开启: SHOW VARIABLES LIKE slow_query_log; 如果返回值是OFF,你需要开启它。 2. 开启慢查询日志 你可以临时在运…...

HZOJ-266:表达式计算
题目描述 给出一个表达式,其中运算符仅包含 ,-,*,/,^ 要求求出表达式的最终值。 数据可能会出现括号情况,还有可能出现多余括号情况,忽略多余括号,正常计算即可; 数据保证不会出现大于 max long int 的数据࿱…...

JavaScript学习小结
变量声明:使用var关键字,变量没有类型,但值有类型(弱类型语言) 数据类型: ①number ②string(单引号,双引号都可以表示字符串) ③boolean ④Object类型 ⑤undefine…...
MySQL学习笔记13
DISTINCT数据去重: 案例:获取tb_student学生表学员年龄的分布情况。 mysql> select * from tb_student; ------------------------------------------------- | id | name | age | gender | address | --------------------------…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
