数据结构-顺序栈C++示例
栈(stack)是限定仅在表尾进行插入或删除操作的线性表。
对栈来说,表尾端称为栈顶(top), 表头端称为栈底(bottom),不含元素的空表称为空栈。
假设栈 S = ( a 1 , a 2 , a 3 , ⋯ , a n ) S=(a_1,a_2,a_3,\cdots,a_n) S=(a1,a2,a3,⋯,an) , 则称 a 1 a_1 a1为栈底元素, a n a_n an为栈顶元素,插入元素到栈顶(即表尾)的操作称为入栈, 从栈顶(即表尾)删除最后一个元素的操作称为出栈。栈元素的修改是按后进先出的原则进行的,因此栈又称为后进先出(Last In First Out, LIFO)的线性表。
由于栈固有的后进先出特性,使得栈称为程序设计中的有用工具,另外,如果问题求解的过程具有“后进先出”的天然特性的话,则求解的算法中也需要利用“栈”, 如:
- 数制转换
- 表达式求值
- 括号匹配的检验
- 八皇后问题
- 行编辑程序
- 函数调用
- 迷宫求解
- 递归调用的实现
抽象数据类型定义
ADT Stack{ 数据对象: D = { a i ∣ a i ∈ E l e m S e t , i = 1 , 2 , 3 , ⋯ , n , n ≥ 0 } D=\{{a_i}| a_i \in ElemSet, i=1,2,3,\cdots,n, n \geq 0\} D={ai∣ai∈ElemSet,i=1,2,3,⋯,n,n≥0}
数据关系: R = { < a i − 1 , a i > ∣ a i − 1 , a i ∈ D , i = 1 , 2 , 3 , ⋯ , n } R=\{<a_{i-1}, a_i> | a_{i-1},a_i \in D, i = 1,2,3,\cdots,n\} R={<ai−1,ai>∣ai−1,ai∈D,i=1,2,3,⋯,n}
约定 a n a_n an 端为栈顶, a 1 a_1 a1 端为栈底。
基本操作:
InitStack(&S) 操作结果:构造一个空栈 S S S
DestroyStack(&S) 初始条件:栈 S S S已经存在
操作结果:栈 S S S被销毁
ClearStack(&S) 初始条件:栈 S S S已经存在
操作结果:将栈 S S S 清空
StackEmpty(&S) 初始条件:栈 S S S已经存在
操作结果:若栈 S S S 为空栈,则返回
true, 否则返回false
StackLength(&S) 初始条件:栈 S S S已经存在
操作结果:返回栈 S S S 的元素个数,即栈的长度
GetTop(&S) 初始条件:栈 S S S已经存在且非空
操作结果:返回栈 S S S 的栈顶元素
Push(&S,e) 初始条件:栈 S S S已经存在
操作结果:插入元素
e为新的栈顶元素
Pop(&S,e) 初始条件:栈 S S S已经存在且非空
操作结果:删除
S的栈顶元素,并且用e返回其值
StackTraverse(&S,e) 初始条件:栈 S S S已经存在且非空
操作结果:从栈底到栈顶一次对
S的每个数据元素进行访问
}ADT Stack
顺序栈
顺序栈是指利用顺序存储结构实现的栈。
初始化
bool InitStack(SqStack &S)
{S.base = new SElemType[MaxSize];if (!S.base){std::cerr << "内存分配失败" << std::endl;return false;}S.front = S.base;S.stacksize = MaxSize;return true;
}
销毁
bool DestroyStack(SqStack &S)
{if (S.base){delete[] S.base;S.stacksize = 0;S.base = S.front = nullptr;return true;}return false;
}
清空
bool ClearStack(SqStack &S)
{if (S.base){S.front = S.base;return true;}return false;
}
是否为空栈
bool StackEmpty(const SqStack &S)
{return S.base == S.front;
}
栈长度
int StackLength(const SqStack &S)
{return S.front - S.base;
}
入栈
bool Push(SqStack &S, const SElemType &e)
{if (S.front - S.base == S.stacksize){std::cerr << "顺序栈已满,无法插入新元素" << std::endl;return false;}*(S.front) = e;S.front++;return true;
}
出栈
bool Pop(SqStack &S, SElemType &e)
{if (StackEmpty(S)){std::cerr << "空栈无法取值" << std::endl;return false;}S.front--;e = *(S.front);return true;
}
获取栈顶元素
SElemType GetTop(const SqStack &S)
{if (StackEmpty(S)){std::cerr << "空栈无法取值" << std::endl;return false;}return *(S.front - 1);
}
遍历栈元素
void StackTraverse(const SqStack &S)
{for (int i = 0; i < S.front - S.base; i++){std::cout << "第 " << i + 1 << " 个元素为: " << S.base[i] << std::endl;}
}
头文件
#pragma once
#include <iostream>const int MaxSize = 100;
typedef int SElemType;
typedef struct _SqStack
{SElemType *base; // 栈底SElemType *front; // 栈顶int stacksize; // 栈可用的最大容量
} SqStack;bool InitStack(SqStack &S);
bool DestroyStack(SqStack &S);
bool ClearStack(SqStack &S);
bool StackEmpty(const SqStack &S);
int StackLength(const SqStack &S);
bool Push(SqStack &S, const SElemType &e);
bool Pop(SqStack &S, SElemType &e);
void StackTraverse(const SqStack &S);
SElemType GetTop(const SqStack &S);
测试文件
#include "include/stack.h"int main()
{SqStack S;InitStack(S);Push(S, 1);Push(S, 2);Push(S, 3);Push(S, 4);StackTraverse(S);SElemType top = GetTop(S);std::cout << "栈顶元素为: " << top << std::endl;int stack_len = StackLength(S);std::cout << "栈长度: " << stack_len << std::endl;Pop(S, top);StackTraverse(S);std::cout << "++++++++++++++" << std::endl;ClearStack(S);StackTraverse(S);DestroyStack(S);return 0;
}
链栈
链栈是指采用链式存储结构实现的栈。通常使用单链表来表示,由于栈的主要操作是在栈顶插入和删除,为了方便,这里将链表的头结点作为栈顶,且不需要头结点。
初始化
bool InitStack(LinkStack &S)
{S = nullptr;return true;
}
销毁
bool DestroyStack(LinkStack &S)
{while (S){StackNode *tmp = S->next;S = S->next;delete tmp;}return true;
}
清空
bool ClearStack(LinkStack &S)
{DestroyStack(S->next);S = nullptr;return true;
}
是否为空栈
bool StackEmpty(const LinkStack &S)
{return !S;
}
栈长度
int StackLength(const LinkStack &S)
{int len = 0;StackNode *tmp = S;while (tmp){len++;tmp = tmp->next;}return len;
}
入栈
bool Push(LinkStack &S, const ElemType &e)
{StackNode *p = new StackNode;p->data = e;p->next = S;S = p;return true;
}
出栈
bool Pop(LinkStack &S, ElemType &e)
{if (S){e = S->data;StackNode *tmp = S;S = S->next;delete tmp;return true;}return false;
}
获取栈顶元素
ElemType GetTop(const LinkStack &S)
{if (S)return S->data;else{return 0;}
}
遍历栈元素
void StackTraverse(const LinkStack &S)
{StackNode *tmp = S;int i = 0;while (tmp){i++;std::cout << "第 " << i << " 个元素为: " << tmp->data << std::endl;tmp = tmp->next;}
}
文章参考 严蔚敏老师《数据结构 C语言版 第2版》和青岛大学王卓数据结构视频课
相关文章:

数据结构-顺序栈C++示例
栈(stack)是限定仅在表尾进行插入或删除操作的线性表。 对栈来说,表尾端称为栈顶(top), 表头端称为栈底(bottom),不含元素的空表称为空栈。 假设栈 S ( a 1 , a 2 , a 3 , ⋯ , a n ) S(a_1,a_2,a_3,\cdots,a_n) S(a1,a2,a3,⋯,an…...
若依cloud -【 100 ~ 103 】
100 分布式日志介绍 | RuoYi 分布式日志就相当于把日志存储在不同的设备上面。比如若依项目中有ruoyi-modules-file、ruoyi-modules-gen、ruoyi-modules-job、ruoyi-modules-system四个应用,每个应用都部署在单独的一台机器里边,应用对应的日志的也单独存…...

可转债实战与案例分析——成功的和失败的可转债投资案例、教训与经验分享
实战与案例分析——投资案例研究 股票量化程序化自动交易接口 一、成功的可转债投资案例 成功的可转债投资案例提供了有价值的经验教训,以下是一个典型的成功案例: 案例:投资者B的成功可转债投资 投资者B是一位懂得风险管理的投资者&#…...
@NotNull注解不生效,全局异常处理
1.引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-validation</artifactId><version>3.1.2</version> </dependency> 2:实体类 实体类属性加上NotNull注解…...

【办公自动化】使用Python一键往Word文档的表格中填写数据(文末送书)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
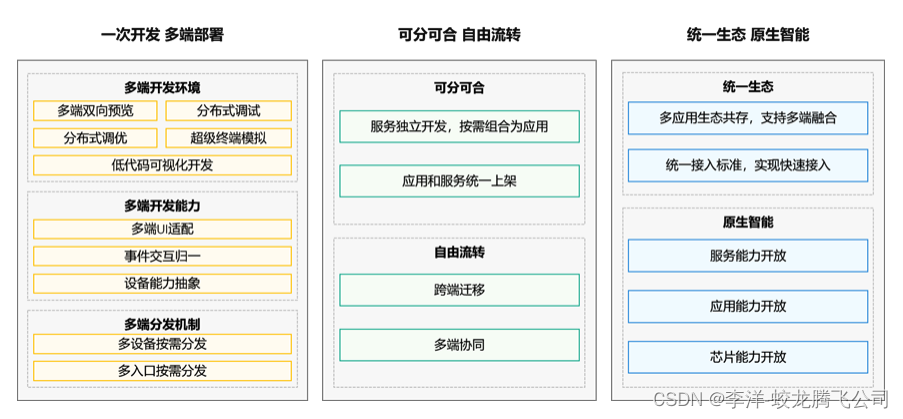
OpenHarmony应用核心技术理念与需求机遇简析
一、核心技术理念 图片来源:OpenHarmony官方网站 二、需求机遇简析 新的万物互联智能世界代表着新规则、新赛道、新切入点、新财富机会;各WEB网站、客户端( 苹果APP、安卓APK)、微信小程序等上的组织、企业、商户等;OpenHarmony既是一次机遇、同时又是一次大的挑战&…...

让Pegasus天马座开发板实现超声波测距
在完成《让Pegasus天马座开发板用上OLED屏》后,我觉得可以把超声波测距功能也在Pegasus天马座开发板上实现。于是在箱子里找到了,Grove - Ultrasonic Ranger 这一超声波测传感器。 官方地址: https://wiki.seeedstudio.com/Grove-Ultrasonic_Ranger 超声…...

C++11 多线程学习
C11学习 一、多线程 1、模板线程是以右值传递的 template <class Fn, class... Args> explicit thread(Fn&& fn, Args&&... args)则需要使用到std::ref和std::cref很好地解决了这个问题,std::ref 可以包装按引用传递的值。 std::cref 可以…...

数学公式测试
MVP变换 MVP变换用来描述视图变换的任务,即将虚拟世界中的三维物体映射(变换)到二维坐标中。 MVP变换分为三步: 模型变换(model tranformation):将模型空间转换到世界空间(找个好的地方,把所…...

机器学习——SVM(支持向量机)
0、前言: SVM应用:主要针对小样本数据进行学习、分类和回归(预测),能解决神经网络不能解决的过学习问题,有很好的泛化能力。(注意:SVM算法的数学原理涉及知识点比较多,所…...

【李沐深度学习笔记】基础优化方法
课程地址和说明 基础优化方法p2 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 基础优化方法 在讲具体的线性回归实现之前,要先讲一下基础的优化模型的方法 梯度下降 当模型没有显示解(…...

tmux 配置vim风格按键,支持gbk编码
vim修改~/.tmux.conf文件,没有则新增,添加如下内容。默认前缀更改为Ctrla。强烈建议更换Caps lock键位与Ctrl键位,用过的都说好,换过就回不来了。 unbind C-b set -g prefix C-a bind a send-prefixset -sg escape-time 1bind r …...
Python —— excel文件操作(超详细)
背景 很多公司还是用excel去管理测试用例的,所以为了减少重复繁琐的导出导出工作,学会如何用代码操作excel表格很实用~ 1、读取excel文件基本步骤 1、操作excel的一些库 1、xlrd:读取库,xlwt:写入,现在…...
什么是AI问答机器人?它的应用场景有哪些?
近年来,由于技术的进步和对个性化客户体验的需求不断增长,AI问答机器人也是获得了巨大的关注。AI问答机器人,也被称为AI聊天机器人,是一种旨在模拟人类对话并通过基于文本或语音的界面与用户交互的计算机程序。其能够自动执行各种…...

静态文件
静态文件 静态文件配置 - settings.py中 1,配置静态文件的访问路径【该配置默认存在】 通过哪个url地址找静态文件 STATIC URL‘/static/’ 说明 指定访问静态文件时是需要通过/static/xxx或http://127.0.0.1:8000/static/xxx [xxx表示具体的静态资源位置] 模…...

Centos7 自部署中间件开机启动,以及java应用开机启动方法
一、zookeeper cd /etc/rc.d/init.d/ touch zookeeper chmod x zookeeper vi zookeeper#以下为内容,自行修改 路径#!/bin/bash ##chkconfig:2345 10 90#description:service zookeeper #修改为自己的目录 export ZOO_LOG_DIR/data/apache-zookeeper-3.7.0/logs…...

密度估计公式
极大似然估计: y p ( x 1 , x 2 , x 3 , . . . , x n ) 1 2 π σ e − ( x 1 − μ ) 2 2 σ 2 1 2 π σ e − ( x 2 − μ ) 2 2 σ 2 . . . 1 2 π σ e − ( x n − μ ) 2 2 σ 2 y p(x_1,x_2,x_3,...,x_n) \frac{1}{\sqrt{2\pi} \sigma} e ^{-\frac{(x_1…...
)
2023 ICPC 网络赛 第一场(补题:F)
7题罚时879, 队排235,校排79。 除了I题dp没注意空间限制第一发没有用滚动数组MLE,以及G题启发式合并脑抽用set当容器T一发,以及K没注意是平方的期望白wa4发这些应当避免的失误外,基本满意。剩下的题基本都是当时写不出…...

MySQL慢查询优化、日志收集定位排查、慢查询sql分析
MySQL慢查询日志收集、定位,慢查询分析、排查。 一 MySQL慢查询定位 1. 确定是否已开启慢查询日志 查看慢查询日志是否已经被开启: SHOW VARIABLES LIKE slow_query_log; 如果返回值是OFF,你需要开启它。 2. 开启慢查询日志 你可以临时在运…...

HZOJ-266:表达式计算
题目描述 给出一个表达式,其中运算符仅包含 ,-,*,/,^ 要求求出表达式的最终值。 数据可能会出现括号情况,还有可能出现多余括号情况,忽略多余括号,正常计算即可; 数据保证不会出现大于 max long int 的数据࿱…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
