LeetCode322. 零钱兑换
322. 零钱兑换
文章目录
- [322. 零钱兑换](https://leetcode.cn/problems/coin-change/)
- 一、题目
- 二、题解
- 方法一:完全背包二维数组
- 方法二:一维数组
- 三、注意
一、题目
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
二、题解
方法一:完全背包二维数组
这个问题可以看作是一个完全背包问题的变形,即每种硬币的数量是无限的,而不是有限的。
-
算法思路:
-
首先,我们要定义一个二维数组
dp,其中dp[i][j]表示用前i+1种硬币(即coins[0]到coins[i])凑成金额j所需的最少硬币个数。 -
然后,我们要初始化
dp数组,对于第一种硬币coins[0],我们只需要看金额j是否能被它整除,如果能,那么dp[0][j] = j / coins[0],否则dp[0][j] = INT_MAX(表示无法凑成)。 -
接下来,我们要逐行更新
dp数组,对于第i+1种硬币coins[i],我们有两种选择:使用它或者不使用它。如果不使用它,那么dp[i][j] = dp[i-1][j],即和前i种硬币的结果一样;如果使用它,那么我们要保证金额j大于等于硬币面额coins[i],并且减去这个面额后的金额能够被前i+1种硬币凑成,即dp[i][j-coins[i]] != INT_MAX,那么dp[i][j] = dp[i][j-coins[i]] + 1,即在减去这个面额后的结果上加一。我们要在这两种选择中取最小值,即dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i]] + 1)。 -
最后,我们要返回
dp[coins.size() - 1][amount],即用所有种类的硬币凑成总金额所需的最少硬币个数。如果这个值等于INT_MAX,说明无法凑成,返回-1;否则返回这个值。
-
-
具体实现:
-
可以用一个嵌套的循环来实现上述算法思路,外层循环遍历硬币种类,内层循环遍历金额。每次更新
dp[i][j]时,先赋值为不使用当前硬币的结果,然后判断是否可以使用当前硬币,并更新为最小值。 -
我们还需要注意一些边界情况,比如当金额为零时,返回零;当硬币数组为空时,返回
-1。
class Solution { public:int coinChange(vector<int>& coins, int amount) {if (amount == 0) return 0;vector<vector<int>> dp(coins.size(), vector<int>(amount + 1, INT_MAX));// 初始化for (int i = 0; i <= amount; i++) {if (i % coins[0] == 0) {dp[0][i] = i / coins[0];}}for (int i = 1; i < coins.size(); i++) {for (int j = 0; j <= amount; j++) {dp[i][j] = dp[i - 1][j];if (j >= coins[i] && dp[i][j - coins[i]]!=INT_MAX) {dp[i][j] = min(dp[i][j], dp[i][j - coins[i]] + 1);}}}return dp[coins.size() - 1][amount] == INT_MAX? -1 : dp[coins.size() - 1][amount];} }; -
-
算法分析:
-
时间复杂度:O(N*M),其中 N 是硬币种类数,M 是总金额。我们需要遍历所有的硬币和金额组合,每次更新一个状态值。
-
空间复杂度:O(N*M),其中 N 是硬币种类数,M 是总金额。需要一个二维数组来存储所有的状态值。
-
方法二:一维数组
算法思路和具体实现和上面的二维数组差不多,不过我也copy了一下~
-
算法思路:
- 首先,我们定义一个一维数组
dp,其中dp[j]表示凑成金额j所需的最少硬币个数。 - 然后,我们初始化
dp数组,对于金额为零的情况,我们不需要任何硬币,所以dp[0] = 0。对于其他金额,我们先设为一个很大的数,比如INT_MAX,表示无法凑成。 - 接下来,我们遍历每种硬币
coins[i],对于每种硬币,我们从小到大遍历金额j,如果j >= coins[i],说明我们可以用这种硬币来凑成金额j,那么我们就比较使用这种硬币和不使用这种硬币的结果,取最小值,即dp[j] = min(dp[j], dp[j - coins[i]] + 1)。注意这里和 01 背包问题的区别,01 背包问题中只能用一次每种物品,所以要从大到小遍历金额,避免重复使用;而完全背包问题中可以用无限次每种物品,所以要从小到大遍历金额,允许重复使用。 - 最后,我们返回
dp[amount],即凑成总金额所需的最少硬币个数。如果这个值等于INT_MAX,说明无法凑成,返回-1;否则返回这个值。
- 首先,我们定义一个一维数组
-
具体实现:
- 这个代码和上一个代码的区别在于,它只用了一个一维数组来存储状态值,而不是一个二维数组。这样做的原因是,对于每种硬币,我们只需要知道上一行的状态值就可以更新当前行的状态值,所以我们可以用一个一维数组来代替二维数组,节省空间。
- 我们可以用一个嵌套的循环来实现上述算法思路,外层循环遍历硬币种类,内层循环遍历金额。每次更新
dp[j]时,先判断是否可以使用当前硬币,并更新为最小值。 - 我们还需要注意一些边界情况,比如当金额为零时,返回零;当硬币数组为空时,返回
-1。
class Solution { public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for (int i = 0; i < coins.size(); i++) {for (int j = 0; j <= amount; j++) {if (j >= coins[i] && dp[j - coins[i]]!=INT_MAX) {dp[j] = min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == INT_MAX? -1 : dp[amount];} }; -
算法分析:
- 时间复杂度:O(N*M),其中 N 是硬币种类数,M 是总金额。我们需要遍历所有的硬币和金额组合,每次更新一个状态值。
- 空间复杂度:O(M),其中 M 是总金额。我们只需要一个一维数组来存储状态值。
三、注意
这道题不在乎硬币是排列还是组合,是因为我们只关心最少的硬币个数,而不关心硬币的顺序。换句话说,我们只要找到一种硬币组合,使得它的总金额等于目标金额,并且硬币个数最少,那么这种组合就是最优解,无论它的硬币顺序如何。例如,如果目标金额是 11 ,硬币面额是 [1, 2, 5] ,那么无论是 [5, 5, 1] 还是 [1, 5, 5] ,都是最优解,因为它们都只用了 3 个硬币。所以,不需要考虑排列和组合的区别,只需要考虑状态转移的逻辑。
相关文章:

LeetCode322. 零钱兑换
322. 零钱兑换 文章目录 [322. 零钱兑换](https://leetcode.cn/problems/coin-change/)一、题目二、题解方法一:完全背包二维数组方法二:一维数组 三、注意 一、题目 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 a…...

AUTOSAR扫盲贴--不是黑神话【基本概念和方法论】
猴子纵有72搬变化,也跳不出如来的手掌 目录 1. 引言 2. AUTOSAR的基本概念 2.1. AUTOSAR的架构和组成部分 2.2. AUTOSAR的规范和...

python抠图(去水印)开源库lama-cleaner入门应用实践
1. 关于 Lama Cleaner Lama Cleaner 是由 SOTA AI 模型提供支持的免费开源图像修复工具。可以从图片中移除任何不需要的物体、缺陷和人,或者擦除并替换(powered by stable diffusion)图片上的任何东西。 特征: 完全免费开源&am…...

Nginx可视化管理工具结合cpolar实现远程访问内网服务
前言 Nginx Proxy Manager 是一个开源的反向代理工具,不需要了解太多 Nginx 或 Letsencrypt 的相关知识,即可快速将你的服务暴露到外部环境,并且支持 SSL 配置。基于 Tabler 的美观且安全的管理界面,无需了解 Nginx 即可轻松创建转发域、重定…...

CCC数字钥匙设计【BLE】 --建立安全测距
1、建立安全测距Establish Secure Ranging 车端总共有三种建立安全测距的方式,具体如下: 1) Optimal Flow 2) Sub-Optimal Flow 3) Ranging Recovery Flow 为了确定建立安全测距需要执行哪条流程,车辆需要进行以下流程选择。当车辆和设备…...

Ubuntu22.04 Opencv4.5.1 CPU和GPU编译攻略,Opencv CPU和GPU编译保姆教程 亲自测试。
1、安装opencv依赖 安装时最好更换一下源。 sudo apt-get -y update sudo apt-get -y install cmake git libgtk2.0-dev pkg-config libavcodec-dev libavformat-dev libswscale-dev sudo apt-get -y install libgtk-3-dev gfortran openexr libatlas-base-dev python3-dev pyt…...

常识判断 --- 党史
目录 中共1~3大 例题 国民党 例题 中共4~5大 例题 中共起义~会议 例题 中共六届六中全会(1938年9月) 中共七大(1945年4月) 例题 中共七届二中全会 例题 中共8~10大 中共11~12届全会 例题 中共13~14大 …...

Rust 基础再理解
Rust堆栈 Rust中各种类型的值默认都存储在栈中,除非显式地使用Box::new()将它们存放在堆上,但数据要存放在栈中,要求其数据类型的大小已知。对于静态大小的类型,可直接存储在栈上,如裸指针、布尔、字符、整数浮点数&a…...
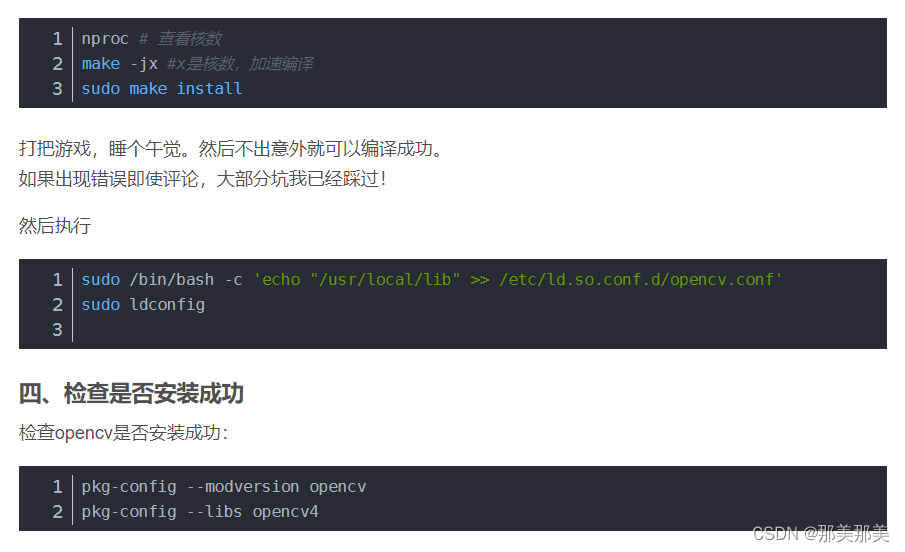
Opencv cuda版本在ubuntu22.04中安装办法,解决Could NOT find CUDNN的办法
文章目录 概要下载cuda的runfile版本配置环境变量官网下载cudann安装Opencv依赖包下载opencv和opencv_contrib并解压准备编译安装anaconda环境执行编译命令安装OpenCV并检查是否安装成功 概要 解决以下安装问题: -- Could NOT find CUDNN: Found unsuitable versi…...

全网首发YOLOv8暴力涨点:Gold-YOLO,遥遥领先,超越所有YOLO | 华为诺亚NeurIPS23
💡💡💡本文独家改进:提出了全新的信息聚集-分发(Gather-and-Distribute Mechanism)GD机制,Gold-YOLO,替换yolov8 head部分 实现暴力涨点 Gold-YOLO | 亲测在多个数据集能够实现大幅涨点 💡💡💡Yolov8魔术师,独家首发创新(原创),适用于Yolov5、Yolov7、…...

BD就业复习第四天
1. 布隆过滤器怎么实现去重 布隆过滤器是一种用于快速检查一个元素是否可能存在于一个大集合中的数据结构,但它并不适用于精确去重。因为布隆过滤器具有一定的误判率(可能会将不存在的元素误判为存在),所以不能确保完全的去重。但…...
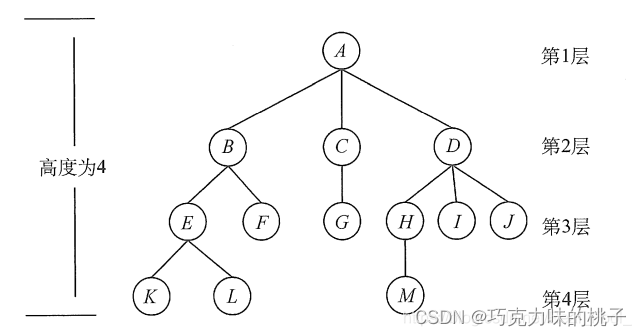
数据结构 | 树
树 树是n(n>0)个结点的有限集。当n 0时,称为空树。在任意一棵非空树中应满足: 有且仅有一个特定的称为根的结点。当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm&#…...
Android11 适配
一、修改targetSdkVersion为30 将build.gradle的目标版本targetSdkVersion修改为30(Android 11) targetSdkVersion 30Android11的改变改变主要影响以Adnroid11 为目标版本的应用(targetSdkVersion>30才有影响),和所…...
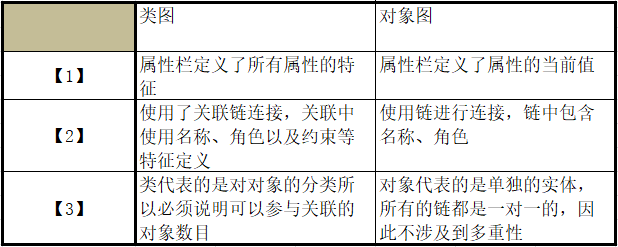
UML基础与应用之对象图
什么是对象图? 对象图表示一组对象及它们之间的关系,是某一时刻系统详细信息的快照,描述系统交互的静态图形,它由协作的对象组成,但不包含在对象之间传递的任何消息。因为对象是类的实例化,所以说某一时刻…...

英码科技精彩亮相火爆的IOTE 2023,多面赋能AIoT产业发展!
9月20日至22日,在这金秋飒爽的季节,为期三天的IOTE 2023第二十届国际物联网展深圳站在深圳国际会展中心盛大举行。英码科技精彩亮相本届展会,并在同期举办的AIoT视觉物联产业生态大会发表了主题演讲,与生态伙伴们共同探讨AIoT产业…...
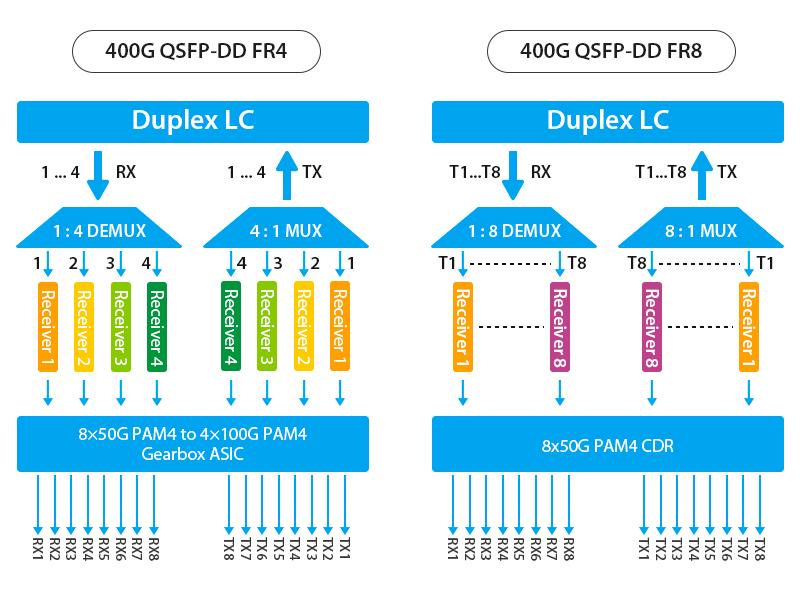
400G QSFP-DD FR4 与 400G QSFP-DD FR8光模块:哪个更适合您的网络需求?
QSFP-DD 光模块随着光通信市场规模的不断增长已成为400G市场中客户需求量最高的产品。其中400G QSFP-DD FR4和400G QSFP-DD FR8光模块都是针对波分中距离传输(2km)的解决方案,它们之间有什么不同?应该如何选择应用?飞速…...
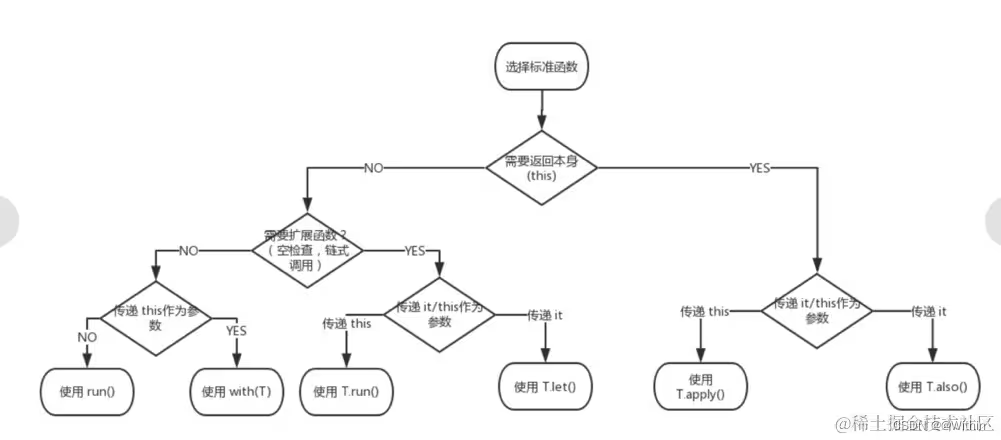
【Android】Kotlin 中的 apply、let、with、also、run 到底有啥区别?
一、图示 二、apply apply 函数接收一个对象并返回该对象本身。它允许您在对象上执行一些操作,同时仍然返回原始对象。 这个函数的语法为: fun <T> T.apply(block: T.() -> Unit): T 其中,T 是对象的类型,block 是一…...

设计模式——职责链模式
职责链模式 职责链模式职责链模式解决什么问题?职责链模式实现 职责链模式 使多个对象都有机会处理请求,从而避免请求的发送者和接收者之间的耦合关系。将这个对象练成一条链,并沿着这条链传递该请求,知道有一个对象处理它为止 …...

小程序自定义tabbar,中间凸起
微信小程序自带tabbar,但无法实现中间按钮凸起样式和功能,因此按照设计重新自定义一个tabbar 1、创建tabbar文件,与pages同级创建一个文件夹,custom-tab-bar,里面按照设计图将底部tabbar样式编写 <view class"tab-bar&q…...

数据结构-顺序栈C++示例
栈(stack)是限定仅在表尾进行插入或删除操作的线性表。 对栈来说,表尾端称为栈顶(top), 表头端称为栈底(bottom),不含元素的空表称为空栈。 假设栈 S ( a 1 , a 2 , a 3 , ⋯ , a n ) S(a_1,a_2,a_3,\cdots,a_n) S(a1,a2,a3,⋯,an…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
