怒刷LeetCode的第8天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:双指针和排序
编辑第二题
题目来源
题目内容
解决方法
方法一:双指针
方法二:递归
方法三:快慢指针
方法四:栈
第三题
题目来源
题目内容
解决方法
方法一:栈
方法二:字符串替换
方法三:链表
方法四:栈和正则表达式
第一题
题目来源
18. 四数之和 - 力扣(LeetCode)
题目内容

解决方法
方法一:双指针和排序
根据题目要求,可以使用双指针和排序法来解决这个问题。
使用双指针解决四数之和问题的算法思路如下:
1、对数组进行排序,将其从小到大排列。
2、使用两重循环分别枚举前两个数,其中第一个数的下标范围是0到n-4,第二个数的下标范围是第一个数的下标加1到n-3。
4、在两重循环中,使用双指针分别指向当前枚举的两个数之后的位置。
5、每次计算四个数的和,并根据和与目标值的比较结果进行如下操作:
- 如果和等于目标值,将四个数加入答案。
- 如果和小于目标值,将左指针右移一位。
- 如果和大于目标值,将右指针左移一位。
- 同时,如果左指针或右指针指向的数字与上一次迭代的数字相同,继续移动指针直到遇到不同的数字。
6、循环结束后,返回所有符合条件的四个数的组合。
class Solution {public List<List<Integer>> fourSum(int[] nums, int target) {List<List<Integer>> quadruplets = new ArrayList<List<Integer>>();if (nums == null || nums.length < 4) {return quadruplets;}Arrays.sort(nums);int length = nums.length;for (int i = 0; i < length - 3; i++) {if (i > 0 && nums[i] == nums[i - 1]) {continue;}if ((long) nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {break;}if ((long) nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {continue;}for (int j = i + 1; j < length - 2; j++) {if (j > i + 1 && nums[j] == nums[j - 1]) {continue;}if ((long) nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {break;}if ((long) nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {continue;}int left = j + 1, right = length - 1;while (left < right) {long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];if (sum == target) {quadruplets.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));while (left < right && nums[left] == nums[left + 1]) {left++;}left++;while (left < right && nums[right] == nums[right - 1]) {right--;}right--;} else if (sum < target) {left++;} else {right--;}}}}return quadruplets;}
}复杂度分析:
- 时间复杂度为O(n^3),其中n是数组的长度。这是因为代码中有两重循环,加上双指针的遍历,总的时间复杂度为O(n^2)。而在双指针的遍历过程中,左右指针最多各自遍历一次数组,所以时间复杂度为O(n)。
- 空间复杂度方面,代码只使用了常数级别的额外空间,主要是存储结果列表,所以空间复杂度为O(1)。
总结起来,该算法的时间复杂度为O(n^3),空间复杂度为O(1)。需要注意的是,在代码中已经进行了一些剪枝操作,以优化算法的效率。
LeetCode运行结果:
 第二题
第二题
题目来源
19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)
题目内容
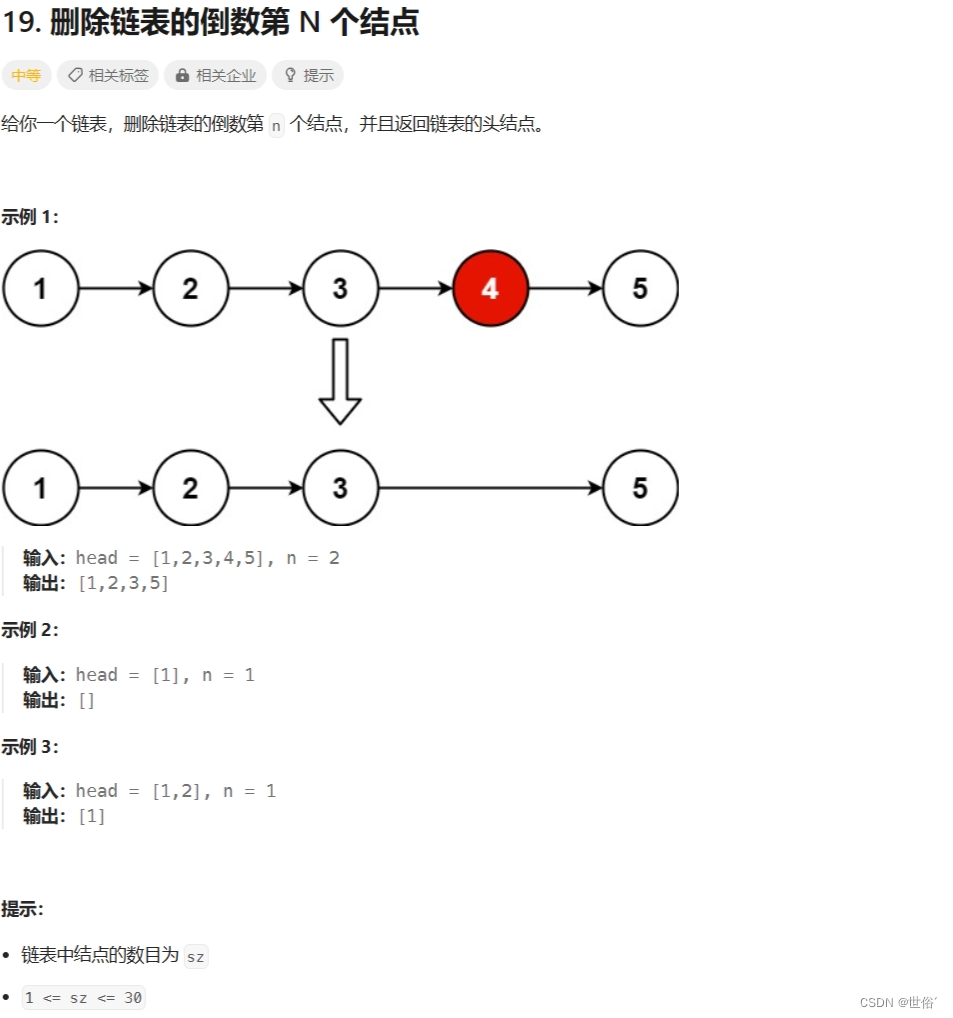

解决方法
方法一:双指针
这道题可以使用双指针来实现。具体做法是,先让第一个指针往前移动n个位置,然后同时移动第一个指针和第二个指针,直到第一个指针到达链表尾部。此时,第二个指针所指向的节点就是要删除的节点的前一个节点,我们只需要将该节点的next指针指向下一个节点,即可完成删除操作。
需要注意的几点是:
- 要处理删除头结点的情况;
- 链表中可能只有一个节点。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {if (head == null) {return null;}ListNode dummy = new ListNode(0, head);ListNode first = head;ListNode second = dummy;for (int i = 0; i < n; i++) {first = first.next;}while (first != null) {first = first.next;second = second.next;}second.next = second.next.next;return dummy.next;
}}复杂度分析:
- 对于给定的链表,我们只需要进行一次遍历即可找到要删除的节点的前一个节点。因此,时间复杂度为O(n),其中n是链表的长度。
- 在空间复杂度方面,我们只使用了常数级别的额外空间,主要是两个指针变量和一个虚拟头节点。因此,空间复杂度为O(1)。
综上所述,该算法的时间复杂度为O(n),空间复杂度为O(1)。
LeetCode运行结果:

方法二:递归
除了双指针法之外,我们还可以使用递归来解决这个问题。具体做法是,在递归的过程中,使用一个计数器来记录当前遍历到的节点位置,并从链表的末尾开始向前遍历。当计数器等于n时,将当前节点的next指针指向下一个节点的next指针,即完成删除操作。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {if (head == null) {return null;}int count = removeHelper(head, n);// 如果计数器等于n,表示要删除的是头结点if (count == n) {return head.next;}return head;
}private int removeHelper(ListNode node, int n) {if (node == null) {return 0;}int count = removeHelper(node.next, n) + 1;// 如果计数器等于n+1,表示要删除的是当前节点的下一个节点if (count == n + 1) {node.next = node.next.next;}return count;
}
}该方法的思路是通过递归实现回溯,每次递归返回当前节点所处的位置。在返回的过程中,不断判断计数器的值是否等于n或n+1,并进行相应的删除操作。
复杂度分析:
- 时间复杂度:在递归过程中,需要遍历整个链表,即O(n)次递归调用。每次递归操作都需要O(1)的时间,因此总体时间复杂度为O(n)。
- 空间复杂度:递归调用会占用栈空间,最坏情况下,递归的深度为链表的长度n,因此空间复杂度为O(n),除去递归栈空间外,不需要额外的空间。
LeetCode运行结果:
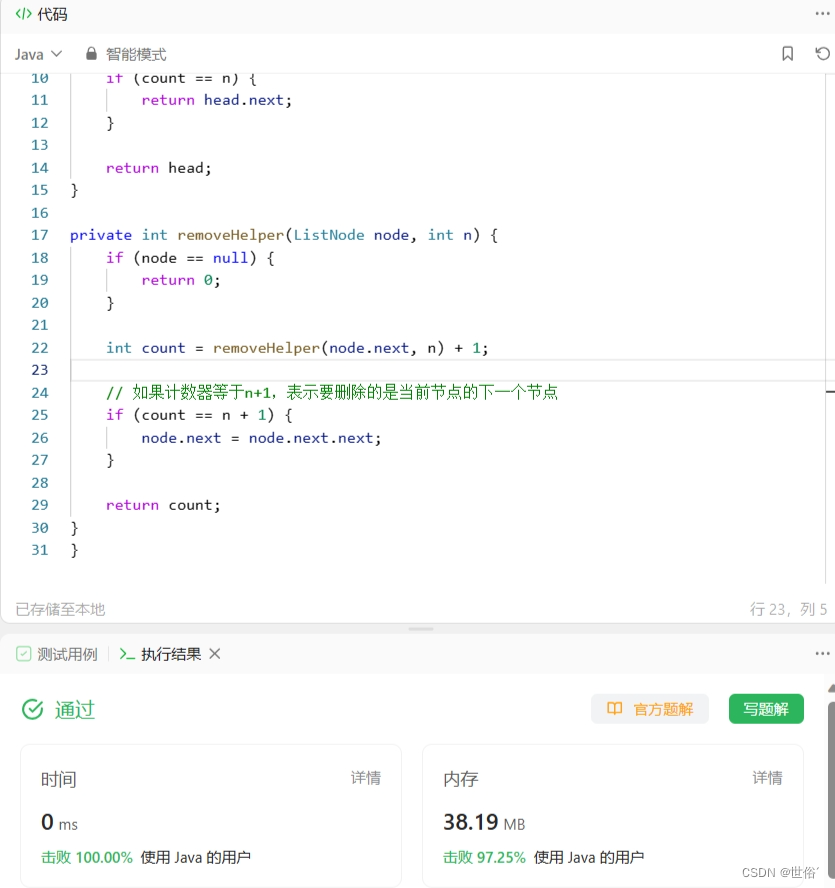
方法三:快慢指针
另一种常见的思路是使用快慢指针。首先,我们让快指针向前移动n个位置。然后,同时移动快指针和慢指针,直到快指针达到链表尾部。此时,慢指针所指的节点就是要删除的节点的前一个节点,我们只需将其next指针指向下一个节点,即可完成删除操作。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {if (head == null) {return null;}ListNode dummy = new ListNode(0, head);ListNode fast = dummy;ListNode slow = dummy;// 快指针先向前移动n个位置for (int i = 0; i < n; i++) {fast = fast.next;}// 同时移动快慢指针,直到快指针达到链表尾部while (fast.next != null) {fast = fast.next;slow = slow.next;}// 删除目标节点slow.next = slow.next.next;return dummy.next;
}}该方法的思路是通过快慢指针的差距来定位要删除的节点的前一个节点。快指针先向前移动n个位置,然后同时移动快慢指针,直到快指针到达链表尾部。这样,慢指针所指的节点就是要删除的节点的前一个节点。
复杂度分析:
- 时间复杂度:需要遍历整个链表,除了初始化指针外,只需一次遍历即可完成任务。因此时间复杂度为O(n)。
- 空间复杂度:只使用了常数级别的额外空间,即定义的指针变量,因此空间复杂度为O(1)。
注意:递归解法和快慢指针解法的时间复杂度都是O(n),其中递归解法的空间复杂度为O(n),而快慢指针解法的空间复杂度为O(1)。因此,在大多数情况下,推荐使用快慢指针解法,因为它的空间复杂度更低。
LeetCode运行结果:
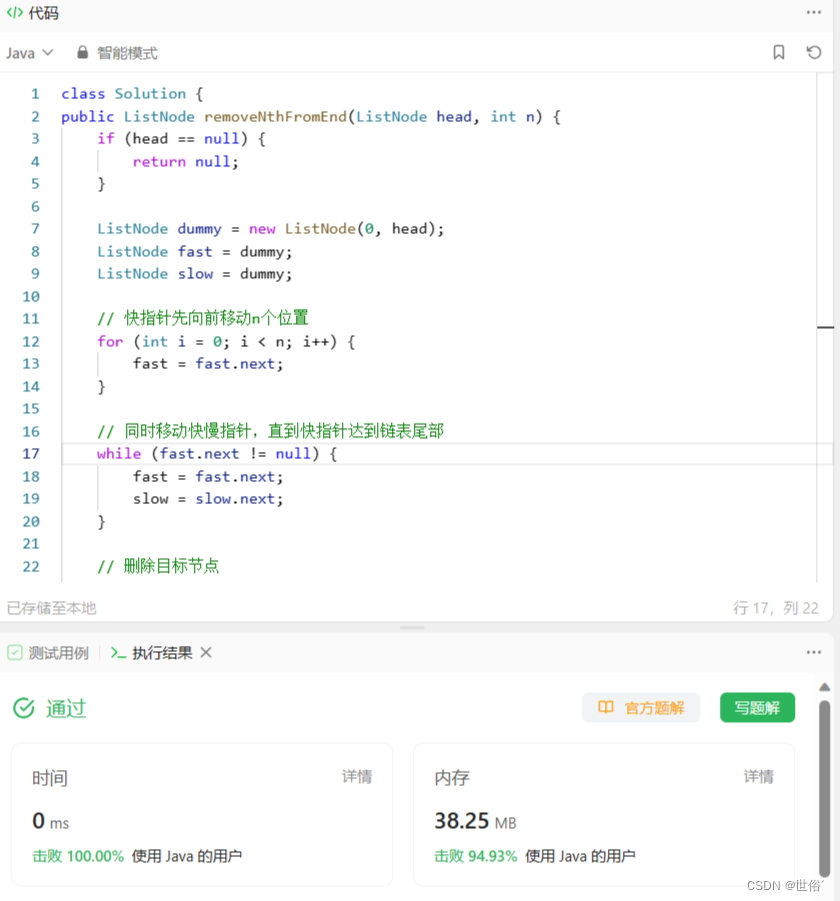
方法四:栈
- 首先,遍历链表并将每个节点都压入栈中。
- 然后,从栈顶开始弹出节点,同时计数。
- 当计数等于n时,表示栈顶节点就是要删除的节点。此时,只需修改相应的指针即可完成删除操作。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {if (head == null) {return null;}Stack<ListNode> stack = new Stack<>();ListNode dummy = new ListNode(0);dummy.next = head;ListNode current = dummy;// 将链表节点依次压入栈中while (current != null) {stack.push(current);current = current.next;}// 弹出第n个节点,并删除for (int i = 0; i < n; i++) {stack.pop();}ListNode prev = stack.peek();prev.next = prev.next.next;return dummy.next;
}
}复杂度分析:
- 时间复杂度:遍历链表将节点压入栈中需要O(n)的时间,弹出第n个节点并删除需要O(n)的时间,因此总体时间复杂度为O(n)。
- 空间复杂度:创建了一个栈来存储链表节点,栈的空间消耗取决于链表的长度,所以空间复杂度为O(n)。
综上所述,使用栈解法删除链表中倒数第n个节点的时间复杂度为O(n),空间复杂度为O(n)。相较于快慢指针解法的O(1)的空间复杂度,栈解法的空间复杂度较高。因此,在大多数情况下,推荐使用快慢指针解法。
LeetCode运行结果:
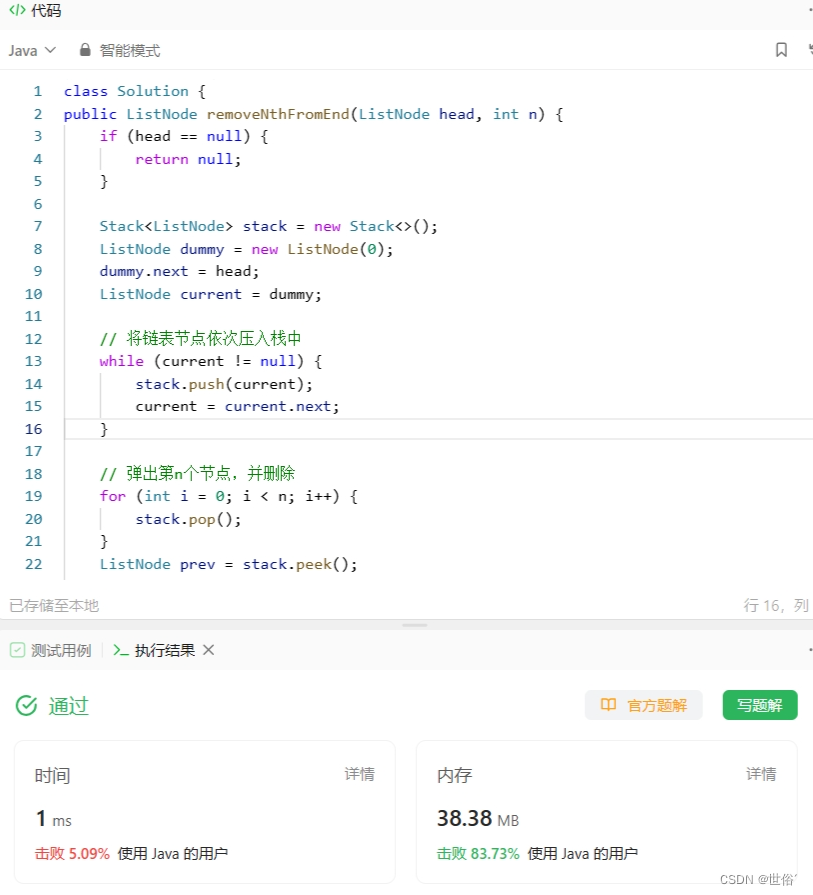
第三题
题目来源
20. 有效的括号 - 力扣(LeetCode)
题目内容

解决方法
方法一:栈
这个问题可以使用栈来解决。我们可以遍历字符串,当遇到左括号时,将其入栈,当遇到右括号时,判断栈顶元素是否与当前右括号匹配。如果匹配,则将栈顶元素出栈,继续遍历;如果不匹配或栈为空,则说明字符串无效。
import java.util.Stack;
class Solution {public boolean isValid(String s) {Stack<Character> stack = new Stack<>();for (char c : s.toCharArray()) {if (c == '(' || c == '{' || c == '[') { // 遇到左括号,入栈stack.push(c);} else if (c == ')' || c == '}' || c == ']') { // 遇到右括号,判断是否匹配if (stack.isEmpty()) {return false; // 栈为空,无法匹配}char top = stack.pop(); // 弹出栈顶元素if ((c == ')' && top != '(') ||(c == '}' && top != '{') ||(c == ']' && top != '[')) {return false; // 括号不匹配}}}return stack.isEmpty(); // 如果栈为空,则所有括号都匹配成功
}
}复杂度分析:
在遍历字符串时,时间复杂度为O(n),其中n是字符串的长度。同样,使用了一个栈来存储字符,空间复杂度也为O(n)。因此,该解法的时间复杂度和空间复杂度均为O(n)。
LeetCode运行结果:

方法二:字符串替换
可以使用字符串替换的方式来判断括号是否匹配。具体思路是:不断替换匹配的括号对"()"、"{}"和"[]"为空字符串,直到字符串中不再包含任何括号对,若最终字符串为空,则说明括号是匹配的。
class Solution {
public boolean isValid(String s) {int length;do {length = s.length();s = s.replace("()", "").replace("{}", "").replace("[]", "");} while (length != s.length());return s.isEmpty();
}
}复杂度分析:
在每次替换操作后,字符串的长度会减少,因此时间复杂度取决于替换操作的次数。最坏情况下,需要进行n/2次替换,其中n是字符串的长度,因此时间复杂度为O(n^2)。由于每次替换操作都会创建新的字符串,因此空间复杂度为O(n)。
需要注意的是:虽然该方法实现简单,但是对于大规模的输入数据,性能可能不理想。因此,在实际应用中,更常用的是栈方法。
LeetCode运行结果:

方法三:链表
可以使用链表来模拟栈的操作,从而判断括号是否匹配。具体思路是:遍历字符串,当遇到左括号时,将其入栈(即链表的头部插入节点),当遇到右括号时,判断栈顶节点与当前右括号是否匹配,如果匹配则出栈(即删除链表的头节点),否则返回false。最后,如果栈为空,则说明所有括号都已匹配。
class Solution {
public boolean isValid(String s) {LinkedList<Character> stack = new LinkedList<>();for (char c : s.toCharArray()) {if (c == '(' || c == '[' || c == '{') {stack.push(c); // 入栈} else if (c == ')' || c == ']' || c == '}') {if (stack.isEmpty() || !isPair(stack.peek(), c)) {return false; // 栈为空或者不匹配,返回false}stack.pop(); // 出栈}}return stack.isEmpty(); // 栈为空,说明所有括号匹配
}private boolean isPair(char left, char right) {return (left == '(' && right == ')') ||(left == '[' && right == ']') ||(left == '{' && right == '}');
}}复杂度分析:
- 在遍历字符串的过程中,每次入栈、出栈操作的时间复杂度为O(1),因此总体时间复杂度是O(n)。
- 链表的空间复杂度与字符串的长度相关,如果所有的字符都是左括号,那么链表的节点个数就是字符串的长度;如果所有的字符都是右括号,链表为空。因此,空间复杂度是O(n)。
需要注意的是,这种方法使用链表模拟栈,可能会产生额外的空间开销。相比直接使用栈数据结构,链表方式相对繁琐一些,并且在插入和删除节点时,需要更多的时间开销。
LeetCode运行结果:
方法四:栈和正则表达式
import java.util.Stack;
import java.util.regex.Pattern;
import java.util.regex.Matcher;
class Solution {public static boolean isValid(String s) {Pattern pattern = Pattern.compile("\\(\\)|\\[\\]|\\{\\}"); // 匹配括号对的模式Matcher matcher;Stack<Character> stack = new Stack<>();while (!s.isEmpty()) {matcher = pattern.matcher(s);if (matcher.find()) {s = matcher.replaceAll(""); // 替换匹配到的括号对为空字符串} else {char c = s.charAt(0);if (c == '(' || c == '[' || c == '{') {stack.push(c); // 左括号入栈} else if (c == ')' || c == ']' || c == '}') {if (stack.isEmpty() || !isPair(stack.pop(), c)) {return false; // 栈为空或者不匹配,返回false}}s = s.substring(1); // 删除已处理的字符}}return stack.isEmpty(); // 栈为空,说明所有括号匹配}private static boolean isPair(char left, char right) {return (left == '(' && right == ')')|| (left == '[' && right == ']')|| (left == '{' && right == '}');}public static void main(String[] args) {String s = "(([]){})";System.out.println(isValid(s)); // 输出 true}}这个方法首先使用正则表达式匹配并替换字符串中的括号对为空字符串,直到字符串中不再包含任何括号对。此后,使用栈来判断剩余的括号是否匹配。最终,如果栈为空,则说明所有括号都已匹配。
请注意,虽然这个方法利用了正则表达式来部分处理括号对的情况,但它依然使用了栈来判断括号是否匹配。这是因为正则表达式无法处理嵌套较深的括号结构。
复杂度分析:
时间复杂度分析:
- 正则表达式匹配和替换的时间复杂度:在每次循环中,使用正则表达式的
replaceAll方法替换字符串中的括号对。假设字符串长度为n,那么这个操作的时间复杂度是O(n)。 - 循环次数的上界:在最坏情况下,当括号都是成对出现且互相嵌套时,需要执行n/2次循环。因此,循环的时间复杂度是O(n)。
- 栈的操作的时间复杂度:在每次循环中,可能进行一次栈的压入或弹出操作,时间复杂度是O(1)。整个算法执行的过程中,最多进行n/2次栈操作,因此栈的时间复杂度是O(n)。
综上所述,基于正则表达式和栈的方法的总体时间复杂度是O(n)。
空间复杂度分析:
- 正则表达式对象的空间复杂度:创建一个Pattern对象来表示匹配括号对的正则表达式,其空间复杂度是O(1)。
- 栈的空间复杂度:在最坏情况下,当所有的括号都是左括号时,栈的深度是n/2。因此,栈的空间复杂度是O(n)。
- 其他临时变量的空间复杂度:除了栈之外,算法只使用了常数级别的额外空间。因此,其他临时变量的空间复杂度是O(1)。
综上所述,基于正则表达式和栈的方法的总体空间复杂度是O(n)。
需要注意的是:这些复杂度分析是基于最坏情况下的分析结果。在实际应用中,具体的时间复杂度和空间复杂度可能会有所不同,具体取决于输入字符串的特点。
LeetCode运行结果:
相关文章:

怒刷LeetCode的第8天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:双指针和排序 编辑第二题 题目来源 题目内容 解决方法 方法一:双指针 方法二:递归 方法三:快慢指针 方法四:栈 第三题 题目来源 题目内容 解决方法…...

Vue Hooks 让Vue开发更简单与高效
Vue Hooks 让Vue开发更简单与高效 介绍 Vue Hooks 是一个基于 Vue.js 的插件,它提供了一种新的方式来编写 Vue 组件,使得开发更加简单和高效。它借鉴了 React Hooks 的概念,通过使用 Hooks,我们可以在不编写类组件的情况下&…...

Go编程规范
文章目录 注释转义符定义变量方法一:指定变量类型,声明后若不赋值,使用默认值方法二:根据值自行判定变量类型(类型推导)方法三:省略var, 注意:左侧的变量不应该是已经声明过的,否则会导致编译错误[推荐]全局…...
premiere 新建 视频导入 视频拼接 视频截取 多余视频删除
1 新建项目 文件 -> 新建 -> 项目 2 导入 2.1 方法一 直接从本地 将 文件拖入对应的文件夹 2.2 方法二 鼠标右键在指定素材文件夹, 选择导入 选择对应本地文件夹对应素材 3 预设 -> 粗剪 -> 在指定模块处 创建序列预设 3.1 指定模块处 鼠标右键 -> 新建项目…...

笔记01:第一行Python
NameError 名字不含特殊符号(只能是英文、数字、下划线、中文等)名字区分大小写名字先定义后使用 SyntaxError 不符合Python语法书写规范除了语法成分中的保留拼写错误输出中文符号if、for、def等语句末尾忘记冒号 IdentationError 缩进错误&#x…...

资产连接支持会话分屏,新增Passkey用户认证方式,支持查看在线用户信息,JumpServer堡垒机v3.7.0发布
2023年9月25日,JumpServer开源堡垒机正式发布v3.7.0版本。在这一版本中,在用户管理层面,为了提高使用JumpServer操作资产的效率,JumpServer支持对会话进行分屏操作,用户可以在一个浏览器页面打开多个会话,方…...
分包优化和游客模式)
uniapp项目实践总结(二十二)分包优化和游客模式
导语:这篇主要介绍应用分包和游客模式相关的内容。 目录 应用分包游客模式 应用分包 微信对于小程序的打包压缩后的代码体积是有限制的,网页和 APP 也可以适用分包功能,因此需要进行分包添加以及分包优化。 分包添加 在pages.json文件中…...
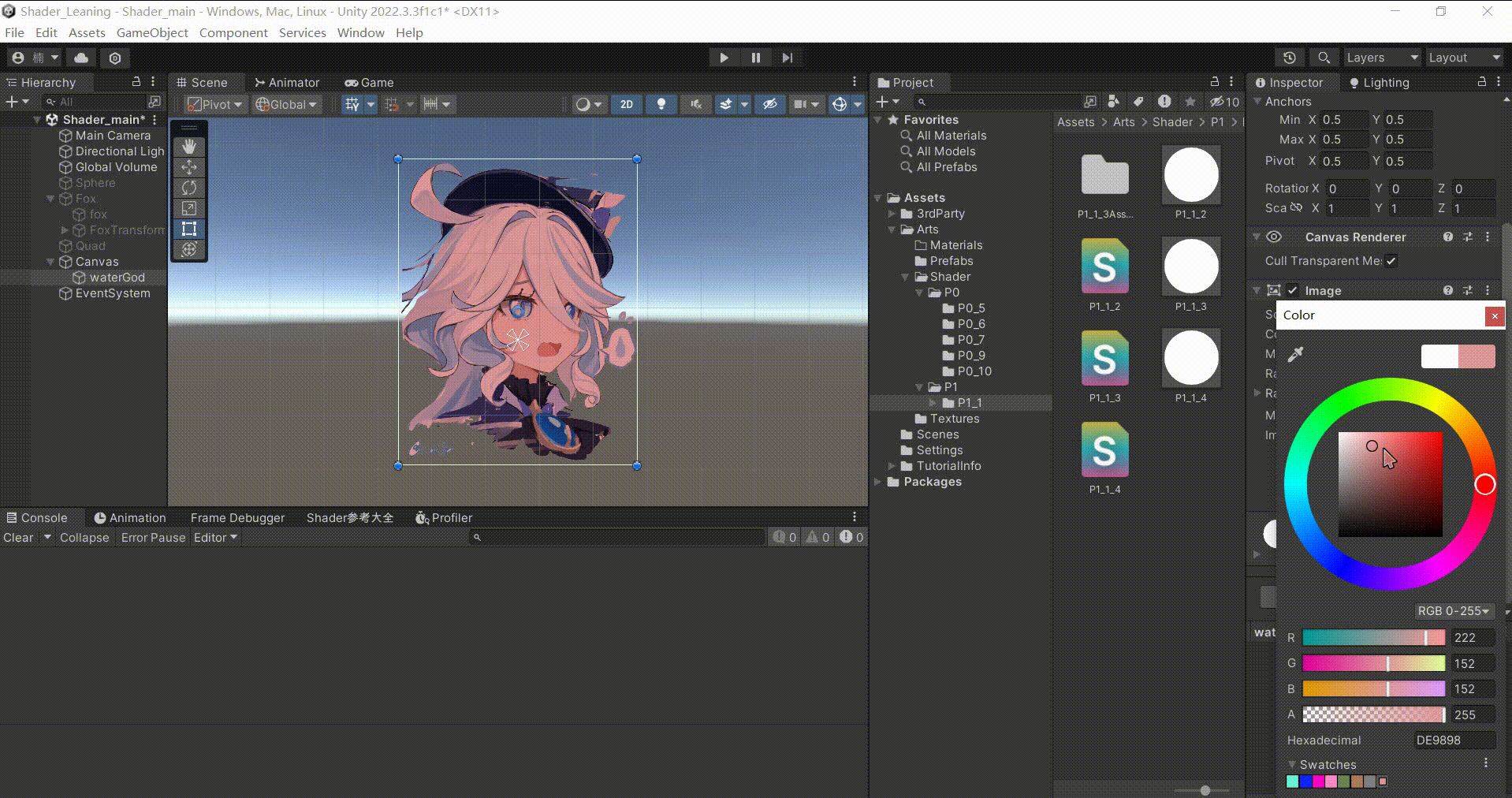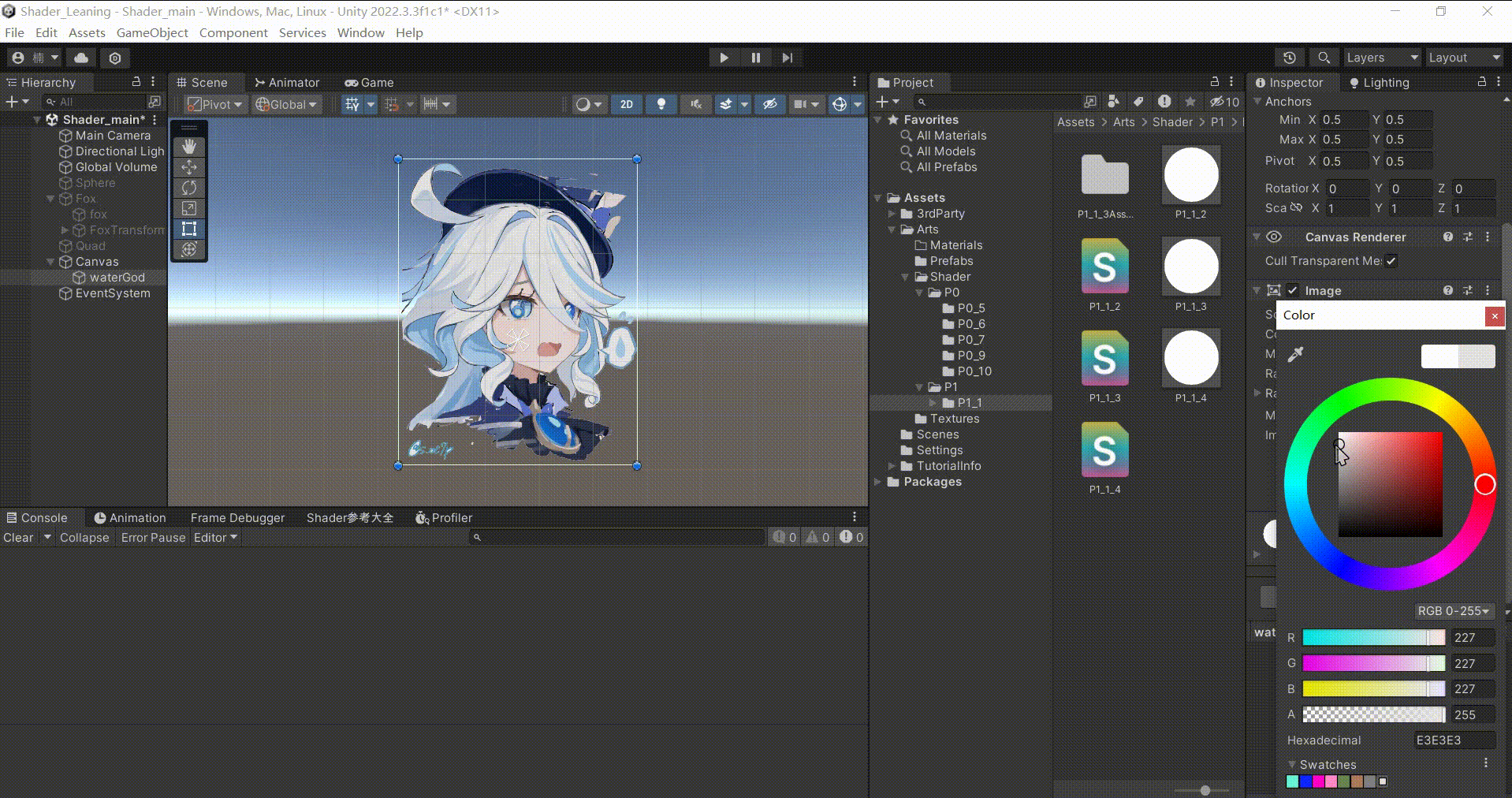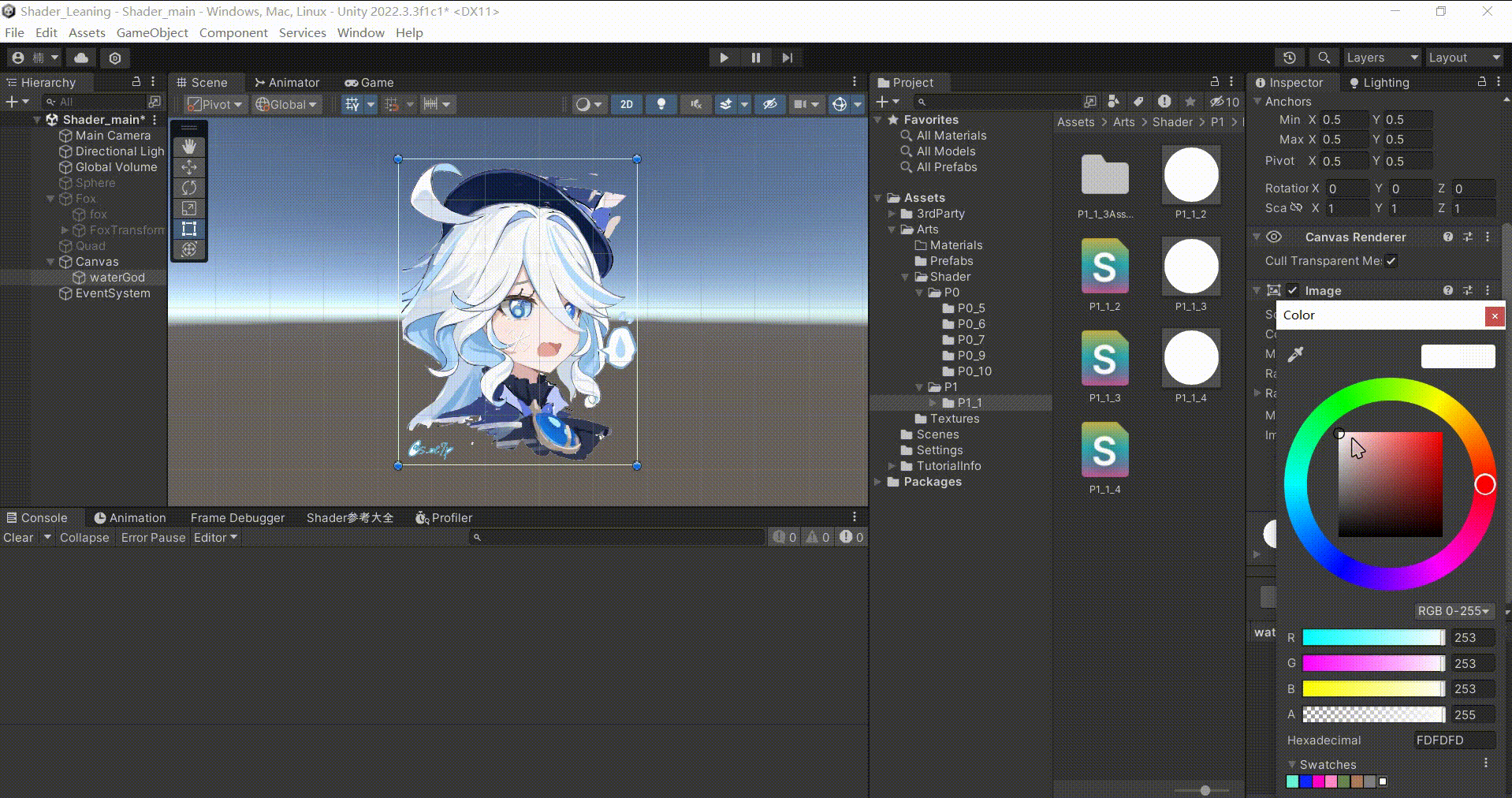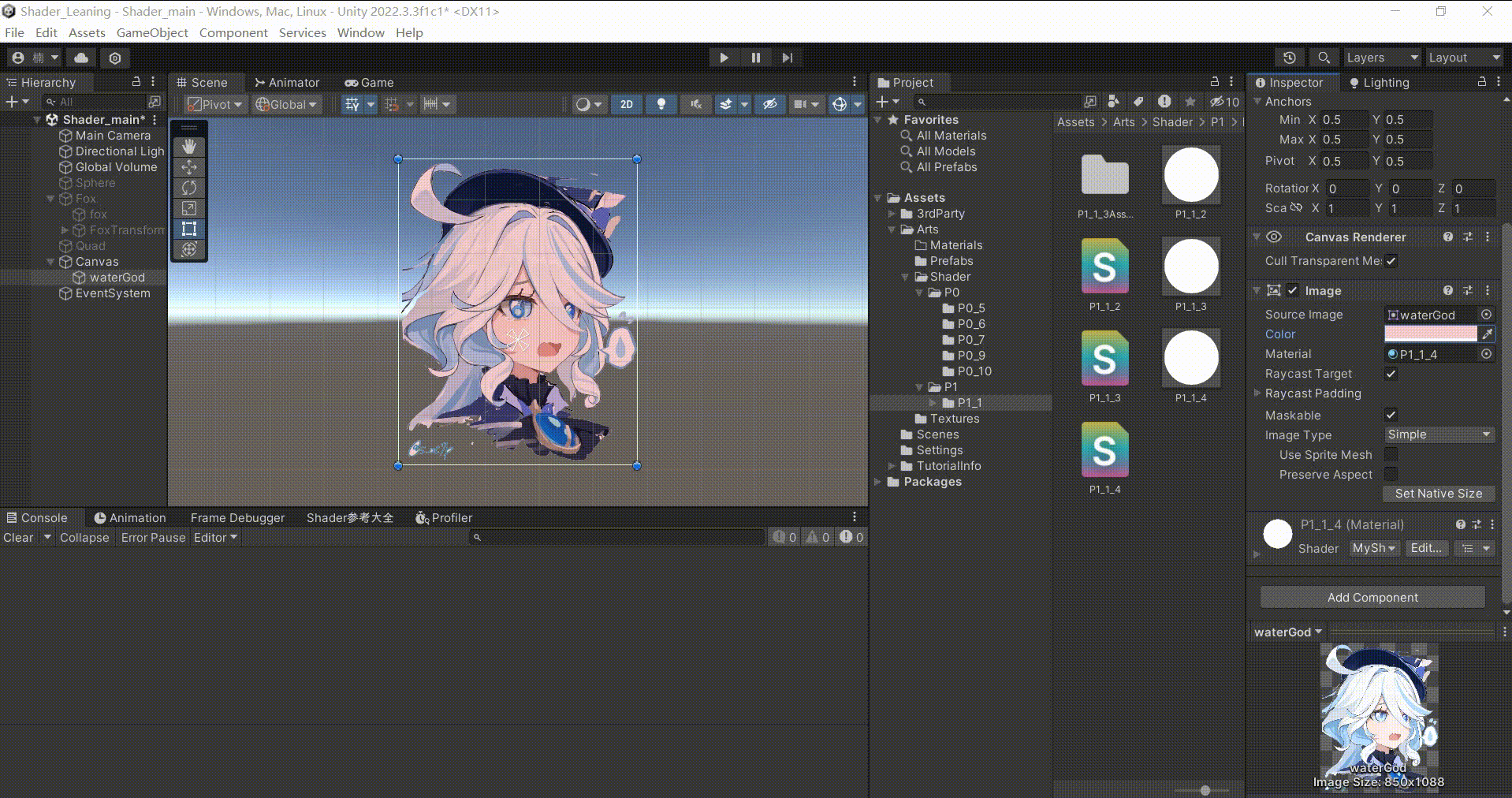
Unity中UI组件对Shader调色
文章目录 前言一、原理在Shader中直接暴露的Color属性,不会与UI的Image组件中的Color形成属性绑定。因为UI的Image组件中更改的颜色是顶点颜色,如果需要在修改组件中的颜色时,使Shader中的颜色也同时改变。那么就需要在应用程序阶段传入到顶点…...

PhpStorm 2023年下载、安装教程和好用插件,保姆级教程
PhpStorm 2023年下载、安装教程和好用插件,保姆级教程 文章目录 PhpStorm 2023年下载、安装教程和好用插件,保姆级教程前言一、安装PhpStorm二、好用的插件简体中文包Chinese(Simplified)Language Pack 三、卸载插件CTRLN 查找类CTRLSHIFTN 全局搜索文件…...
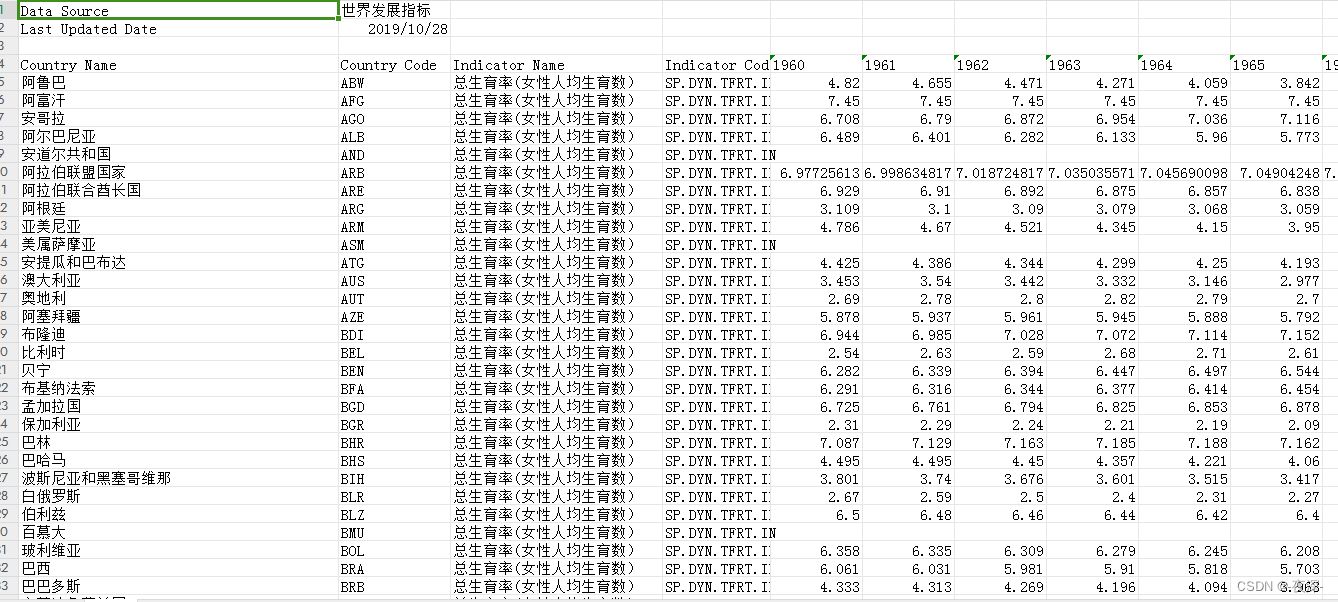
1960-2017年世界各国总和生育率数据
1960-2017年世界各国总和生育率数据 1、时间:1960-2017年 2、指标:生育率 3、范围:全球各国 4、来源:世界银行 5、指标解释: 总生育率表示假设妇女度过整个生育期并按照当期的年龄别生育率生育孩子所生育的孩子数…...

java.math.BigDecimal is not a supported Java type
文章目录 问题描述:结果:原因:Thrif支持的数据类型解决:规范 问题描述: 前端查询后端的pcs总数字段,此字段需要从mydsql的db中获取。PCS字段类型为decimal(26,6),于是打算在response中使用 Big…...

Unity之Hololens开发如何实现UI交互
一.前言 什么是Hololens? Hololens是由微软开发的一款混合现实头戴式设备,它将虚拟内容与现实世界相结合,为用户提供了沉浸式的AR体验。Hololens通过内置的传感器和摄像头,能够感知用户的环境,并在用户的视野中显示虚拟对象。这使得用户可以与虚拟内容进行互动,将数字信…...

二、ubuntu主机端tftp及nfs服务开发环境安装
一.主机端tftp服务环境安装及配置 检查是否已经安装tftp server $dpkg -s tftpd-hpa#如果提示未安装服务,则执行下面安装指令$sudo apt-get install tftpd-hpa tftp-hpa#tftpd-hpa服务端 tftp-hpa客户端创建tftp启动目录,用于存放内核与设备树文件&a…...

Android 12修改usb tp触摸唤醒
前言 Android 12系统休眠时,需要不管接什么型号usb tp都能够触摸唤醒。 Android12系统中,usb tp要能够触摸唤醒,需要在frameworks/native/services/inputflinger/reader/mapper/TouchInputMapper.cpp中将mParameters.wake赋值为trueÿ…...

#define定义标识符详解
0.预定义符号 在讲解#define之前先给大家介绍几个预定义符号 __FILE__ //进行编译的源文件 __LINE__ //文件当前的行号 __DATE__ //文件被编译的日期 __TIME__ //文件被编译的时间 __STDC__ //如果编译器遵循ANSI C(标准C)ÿ…...

开发者必备!如何将闲置iPad Pro打造为编程工具,使用VS Code编写代码
文章目录 前言1. 本地环境配置2. 内网穿透2.1 安装cpolar内网穿透(支持一键自动安装脚本)2.2 创建HTTP隧道 3. 测试远程访问4. 配置固定二级子域名4.1 保留二级子域名4.2 配置二级子域名 5. 测试使用固定二级子域名远程访问6. ipad pro通过软件远程vscode6.1 创建TCP隧道 7. ip…...

【Java 基础篇】Java 模块化详解
Java 9引入了一项重要的功能:模块化(Module System)。模块化是一种将代码和资源封装到可重用和独立的单元中的方法,它有助于改善代码的可维护性、可重用性和安全性。本文将介绍Java模块化的基本概念、如何创建和使用模块以及一些最…...

【2023面试题大全,都是常问面试题】
JAVA基础 面向对象和面向过程的区别 面向过程:基于步骤的编程方式,用函数把这些步骤一步一步地实现,然后在使用的时候一一调用则可 面向对象:基于对象的编程方式,通过定义类来描述对象的属性和行为,面向对…...
Bun 1.0 正式发布,爆火的前端运行时,速度遥遥领先!
文章目录 一、包子1.0二、Bun 是一个一体化工具包为什么包子存在 二、Bun 是一个 JavaScript 运行时Node.js 兼容性速度TypeScript 和 JSX 支持ESM 和 CommonJS 兼容性网络 API热重载插件 一、包子1.0 Bun 1.0终于来了。 Bun 是一个快速、一体化的工具包,用于运行…...

getchar函数设置为非阻塞
一. 前言 我们在学习C语言的时候,getchar都是阻塞的,等待用户输入字符并且输入回车后才返回。但是有时候我们希望把getchar设置为非阻塞,或者说,当我们遇到getchar函数变成非阻塞的了,我们应该怎么解决这个问题&#x…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
