二值贝叶斯滤波计算4d毫米波聚类目标动静属性
机器人学中有些问题是二值问题,对于这种二值问题的概率评估问题可以用二值贝叶斯滤波器binary Bayes filter来解决的。比如机器人前方有一个门,机器人想判断这个门是开是关。这个二值状态是固定的,并不会随着测量数据变量的改变而改变。就像门一样,不是开就是关。
现在我利用二值贝叶斯滤波来在跟踪阶段判断4d毫米波聚类后目标的动态和静态属性
当状态静止时。置信度仅是测量的函数:
b e l t ( x ) = p ( x ∣ z 1 : t , u 1 : t ) = p ( x ∣ z 1 : t ) (1) bel_t(x) = p(x|z_{1:t},u_{1:t}) = p(x|z_{1:t}) \tag 1 belt(x)=p(x∣z1:t,u1:t)=p(x∣z1:t)(1)
这里有两个状态,用 x x x和 ¬ x \neg x ¬x表示,具体来说: b e l t ( ¬ x ) = 1 − b e l t ( x ) bel_t(\neg x)= 1-bel_t(x) belt(¬x)=1−belt(x),状态 x x x不随时间变化。
置信度通常是以概率比的对数(log odds ratio)的形式实现的。 状态x的概率(odds)被定义此事件的概率除以该事件不发生的概率:
p ( x ) p ( ¬ x ) = p ( x ) 1 − p ( x ) (2) \frac{p(x)}{p(\neg x)} = \frac{p(x)}{1-p(x)} \tag 2 p(¬x)p(x)=1−p(x)p(x)(2)
概率对数是这个表达式的对数:
l ( x ) : = p ( x ) 1 − p ( x ) (3) l(x): = \frac{p(x)}{1-p(x)} \tag 3 l(x):=1−p(x)p(x)(3)
概率对数假设值为 − ∞ ∼ ∞ - \infty \sim \infty −∞∼∞,避免了概率接近0或1引起的截断问题
事实上,任何对测量做出反应的变量的递增和递减都可以解释为贝叶斯滤波的概率对数形式。该二值贝叶斯滤波利用一个反向测量模型 p ( x ∣ z t ) p(x|z_t) p(x∣zt)代替熟悉的前向测量模型 p ( z t ∣ x ) p(z_t|x) p(zt∣x)。反向测量模型将关于(二值)状态变量的一个分布指定为测量 z t z_t zt的一个函数。
l t = l t − 1 + l o g p ( x ∣ z t ) 1 − p ( x ∣ z t ) − l o g p ( x ) 1 − p ( x ) (4) l_t = l_{t-1} + log \frac{p(x|z_t)}{1-p(x|z_t)} - log \frac{p(x)}{1-p(x)} \tag 4 lt=lt−1+log1−p(x∣zt)p(x∣zt)−log1−p(x)p(x)(4)
l t l_t lt是状态变量的后验置信度的概率对数,该二值状态变量不随时间变化
根据式(3)概率对数的定义证明,置信度 b e l t ( x ) bel_t(x) belt(x)可以根据概率比对数 l t l_t lt通过下面的方式来求得:
b e l t ( x ) = 1 − 1 1 + e x p { l t } bel_t(x) = 1- \frac{1}{1+exp\{l_t\}} belt(x)=1−1+exp{lt}1
下面证明二值贝叶斯滤波算法的正确性:


在动态和静态属性更新中, p ( x ∣ z t ) p(x|z_t) p(x∣zt)计算为速度大于给定值 v d v_d vd的点数与目标点云中的点总数的比值。
t=0: 机器人对外界环境一无所知,p(x=静态)= p(x=动态)= 0.5
今天写代码验证效果!!!
参考:
- Thrun, S. Probabilistic Robotics. Commun. ACM 2002, 45, 52–57
- Tracking of Multiple Static and Dynamic Targets for 4D Automotive Millimeter-Wave Radar Point Cloud in Urban Environments. Remote. Sens. 15(11): 2923 (2023)
相关文章:

二值贝叶斯滤波计算4d毫米波聚类目标动静属性
机器人学中有些问题是二值问题,对于这种二值问题的概率评估问题可以用二值贝叶斯滤波器binary Bayes filter来解决的。比如机器人前方有一个门,机器人想判断这个门是开是关。这个二值状态是固定的,并不会随着测量数据变量的改变而改变。就像门…...

【刷题笔记9.25】LeetCode:相交链表
LeetCode:相交链表 一、题目描述 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 二、分析及代码 方法一:使用哈希Set集合 (注意…...

打造本地紧密链接的开源社区——KCC@长沙开源读书会openKylin爱好者沙龙圆满举办...
2023年9月9日,由开源社联合 openKylin 社区举办的 KCC长沙开源读书会&openKylin 爱好者沙龙,在长沙圆满举办。这是 KCC长沙首次正式进入公众视野,开展开源交流活动,也是 openKylin 社区长沙首场线下沙龙。长沙地区及其周边的众…...
)
Python 笔记03(多线程)
一 打开命令行,查看本机IP windows r 命令行输入:cmd ipconfig 然后查看IPv4的地址:192.168.1*6.1 ipconfig 二 函数式多进程 from multiprocessing import Process import os, timedef func(name):print(进程的ID:, os.g…...
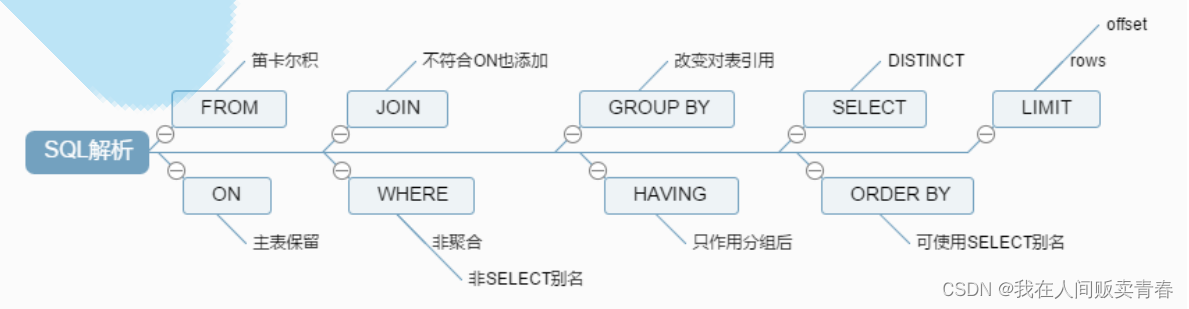
mysql-4:SQL的解析顺序
SQL语句的解析顺序 文章目录 SQL语句的解析顺序编写顺序与解析顺序解析顺序关键字FROMONOUTER JOINWHEREGROUP BYHAVINGSELECTDISTINCTORDER BYLIMIT 解析流程流程分析流程说明WHERE条件解析顺序 编写顺序与解析顺序 编写顺序 SELECT DISTINCT < select_list > FROM &l…...
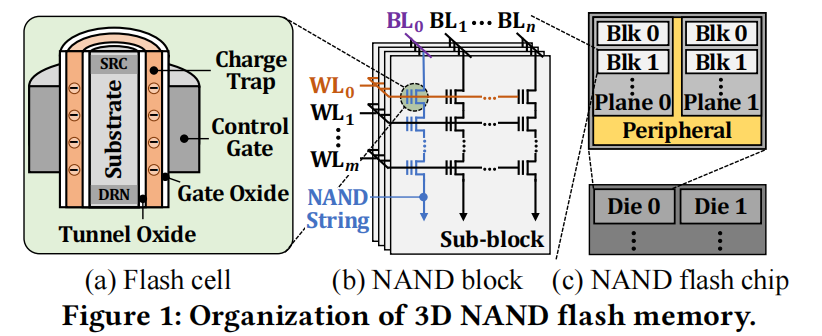
如何通过优化Read-Retry机制降低SSD读延迟?
近日,小编发现发表于2021论文中,有关于优化Read-Retry机制降低SSD读延迟的研究,小编这里给大家分享一下这篇论文的核心的思路,感兴趣的同学可以,可以在【存储随笔】VX公号后台回复“Optimizing Read-Retry”获取下载链接。 本文中主要基于Charge Trap NAND架构分析。NAND基…...

matlab自动生成FPGA rom源码
1 matlab 源码 close all clear all clci=0:1:(300000-100-1); x=300000./(100+i); x=x./2; x=round(...
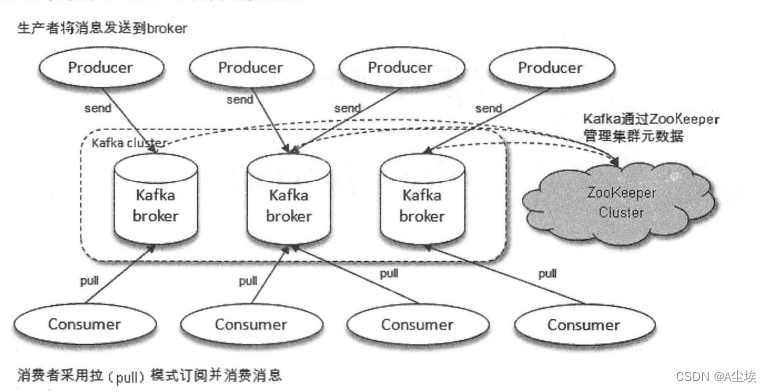
消息队列(RabbitMQ+RocketMQ+Kafka)
消息队列是一种应用程序之间通过异步通信进行数据交换的通信模式 消息队列的类型: 点对点,一对一的消息传递模型,其中每个消息只能被一个接收者消费。发送者将消息发送到队列中,而接收者从队列中获取消息并进行处理,…...

python判断语句
1.布尔类型 进行判断,只有是(True:本质上是一个数字,记作1)和否(False:本质上是一个数字,记作0)。 定义变量存储布尔类型数据: 变量名称 布尔类型字面量 a True代码演示: a True print(type(a))输出结…...

C# 虚方法
在C#中,虚方法(virtual methods)是一种允许派生类(子类)覆盖(重写)基类(父类)中的方法的技术。虚方法的定义和使用如下: 基类中定义虚方法: pub…...
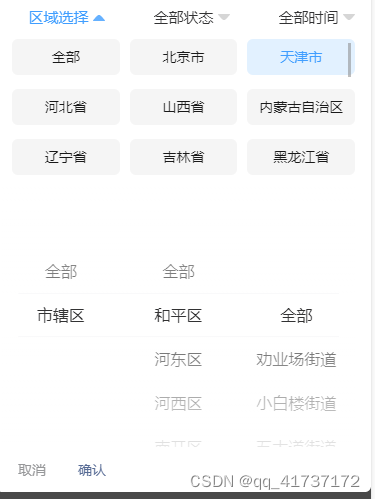
微信小程序,动态设置三级联动, 省市区街道
1.第一步 传parentId0 查询省份 2.第二步 选择省份,传pathId选择省份的pathId, 不传parentId,会查询出 市/县数据 3.第三步 根据选择县的parentId 查询街道数据,传parentId选择的县id 4.选择结果回显 显示所选择的 path 以/分割 取最后一级<van-dropdown-menu…...

Learn Prompt- Midjourney 图片生成:Image Prompts
Prompt 自动生成 前不久,Midjourney 宣布支持图片转 prompt 功能。 原始图片 blueprint holographic design of futuristic Midlibrary --v 5Prompt 生成 直接输入 /describe 指令通过弹出窗口上传图像并发送,Midjourney 会根据该图像生成四种可…...

基于微信小程序的健身房私教预约平台设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言系统主要功能:具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…...
)
安卓Compose(二)
在上一篇博客中,我们已经了解了安卓Compose的一些基本概念以及使用方法,接下来我们将继续深入学习。 一、Compose的基础组件 文本组件(Text) 文本组件是Compose中最基本的组件之一,用于在界面上显示文本。使用方式如下: // 定…...
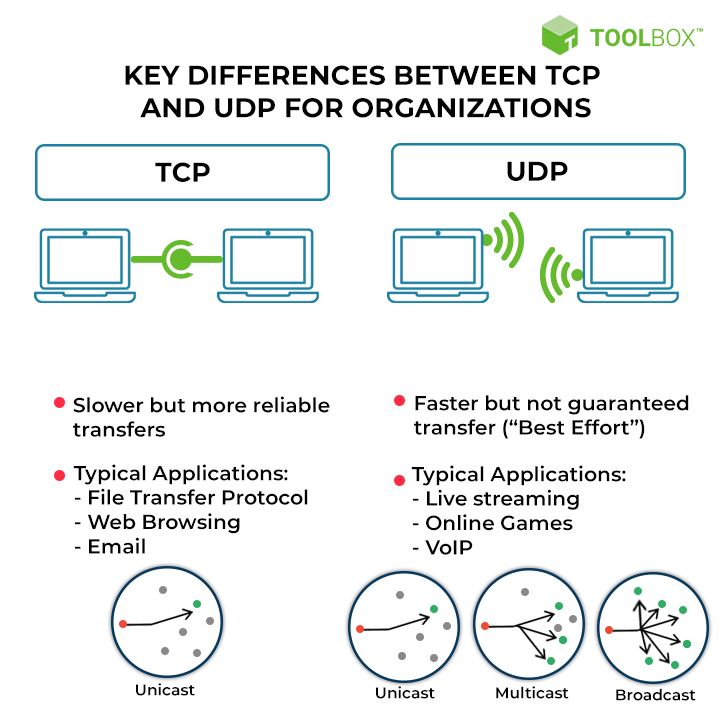
TCP 和 UDP哪个更好
传输控制协议 (TCP) 和用户数据报协议 (UDP) 是互联网的基础支柱,支持从网络源到目的地的不同类型的数据传输。TCP更可靠,而UDP优先考虑速度和效率。本文解释了两种协议的工作原理,并详细讨论了…...

Spring Boot 如何实现单点登录(SSO)
当今的应用程序越来越多地采用了微服务架构,这就引出了一个重要的问题:如何实现单点登录(Single Sign-On,简称SSO)来确保用户在多个微服务之间无需重复登录。Spring Boot是一个流行的Java框架,它提供了一些…...
C#中的(++)和(--)运算符
目录 背景: 的前加 效果展示: 的后加 效果展示 : 总结: 背景: 自增和自减运算符存在于C/C/C#/Java等高级语言中,它的作用是在运算结束前(前置自增自减运算符 )或后(后置自增自减运算符 )将 变量的值加(或减)1。 在C#中,和--是自增和自减运…...

SVG鼠标漫游
鼠标漫游 鼠标漫游就是通过移动光标和滚轮,完成画布缩放、移动的交互过程。 svg 绘图使用原点在左上角的坐标系统,一个单位代表一像素。这里的像素不能简单理解为屏幕像素,是一个用户单位。svg 的 width 和 height 属性决定图像在用户系统的…...

关于Github报SSL_ERROR_SYSCALL的解决方案
最近在运行RN项目的时候发现,在我pod install命令安装pod包时产生了 SSL_ERROR_SYSCALL 的错误,如下所示。 [!] Error installing CocoaAsyncSocket [!] /usr/bin/git clone https://github.com/robbiehanson/CocoaAsyncSocket.git /var/folders/v0/2435fl9178sd4r2_1mdgk_r…...

Redis 集群搭建教程
一、介绍 Redis 集群有着高可用、易扩展、更好的性能等优势,本文主要是实战搭建一个三主三从的 Redis 集群。 正常来说,搭建 Redis 集群需要 6 台服务器。为了简单一点,本文通过一台服务器,6 个端口,搭建一个 Redis …...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
