leetcode 周赛 364
参考视频:
单调栈【力扣周赛 364】
文章目录
- 8048. 最大二进制奇数
- 100049. 美丽塔 I
- 100048. 美丽塔 II
- 100047. 统计树中的合法路径数目
8048. 最大二进制奇数
题目链接
给你一个 二进制 字符串 s ,其中至少包含一个 '1' 。
你必须按某种方式 重新排列 字符串中的位,使得到的二进制数字是可以由该组合生成的 最大二进制奇数 。
以字符串形式,表示并返回可以由给定组合生成的最大二进制奇数。
注意 返回的结果字符串 可以 含前导零。
思路:把第一个 1 放在末尾,其他的 1 从第一个从前往后进行交换,
void swap(char* s, int i, int j) {char t = s[i];s[i] = s[j];s[j] = t;
}char* maximumOddBinaryNumber(char* s) {int length = strlen(s);bool flag = false;int i = 0, j = 0;while (i < length-1) {if (s[i] == '1') {if (!flag) {flag = true;swap(s, i, length - 1);}else {swap(s, i, j);j++;i++;}}else {i++;}}return s;
}
为什么下面这里不管 s[i] 是否等于 s[j]
swap(s, i, j);
j++;
i++;
如果一开始 j 指向了0,那么 i 会往后遍历寻找到下一个 1 ,进行交换后,i、j 都后移 1 位,此时 j 不可能指向 1,因为上一个 1 已经被交换到前面去了。
如果一开始 j 指向了 1 ,那么 i、j 一起后移,直到指向了 0,然后 i 单独后移寻找下一个 1,这就重现了之前的步骤。
也就是说,j 一定会指向在 0 的位置,哪怕它一开始就指向在 1。于是,不会出现 1 和 1交换的情况,除了当前元素与当前元素自身交换时。
100049. 美丽塔 I
题目链接
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。
你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。
如果以下条件满足,我们称这些塔是 美丽 的:
1 <= heights[i] <= maxHeights[i]heights是一个 山状 数组。
如果存在下标 i 满足以下条件,那么我们称数组 heights 是一个 山状 数组:
- 对于所有
0 < j <= i,都有heights[j - 1] <= heights[j] - 对于所有
i <= k < n - 1,都有heights[k + 1] <= heights[k]
请你返回满足 美丽塔 要求的方案中,高度和的最大值 。
1 <= n == maxHeights <= 10^31 <= maxHeights[i] <= 10^9
暴力枚举:每个元素为山顶的情况都枚举一次,计算每一次的数组和,和最大
// 计算数组和
long long calculateSum(int* arr,int length) {long long sum = 0;for (int i = 0; i < length; i++) {sum += arr[i];}return sum;
}long long maximumSumOfHeights(int* maxHeights, int maxHeightsSize) {long long max = 0;int* temp = (int*)malloc(maxHeightsSize * sizeof(int));for (int i = 0; i < maxHeightsSize; i++) {for (int i = 0; i < maxHeightsSize; i++) {temp[i] = maxHeights[i];}// 对 i 左边进行同化,削平山顶for (int j = i; j >= 1; j--) {if (temp[j] < temp[j - 1]) {temp[j - 1] = temp[j];}}// 对 i 右边进行同化for (int j = i; j < maxHeightsSize - 1; j++) {if (temp[j] < temp[j + 1]) {temp[j + 1] = temp[j];}}long long t = calculateSum(temp, maxHeightsSize);max = max > t ? max : t;}free(temp); // 释放动态分配的内存return max;
}
100048. 美丽塔 II
题目链接
给你一个长度为 n 下标从 0 开始的整数数组 maxHeights 。
你的任务是在坐标轴上建 n 座塔。第 i 座塔的下标为 i ,高度为 heights[i] 。
如果以下条件满足,我们称这些塔是 美丽 的:
1 <= heights[i] <= maxHeights[i]heights是一个 山状 数组。
如果存在下标 i 满足以下条件,那么我们称数组 heights 是一个 山状 数组:
- 对于所有
0 < j <= i,都有heights[j - 1] <= heights[j] - 对于所有
i <= k < n - 1,都有heights[k + 1] <= heights[k]
请你返回满足 美丽塔 要求的方案中,高度和的最大值 。
1 <= n == maxHeights <= 10^51 <= maxHeights[i] <= 10^9
思路:单调栈+前后缀数组
维护一个单调栈,栈元素为数组元素下标,对应的值从栈底到栈顶严格递增。
从后往前遍历数组,如果栈非空且当前元素小于等于栈顶元素,那么出栈,直到当前元素大于栈顶元素,更新 sum 值,减去出栈的,注意栈为空的情况。退出循环后,sum 加上要进栈的当前元素,它会覆盖前面 n-i 或 st.top()-previous 个元素。将当前 sum 值加入到 suffix 数组。
从前往后遍历时要完成的操作目的是一样的。
最后,选出 suffix[i]+prefix[i]-maxHeights[i] 最大的值。
#include<iostream>
#include<stack>
#include<vector>
#include<math.h>
using namespace std;
typedef long long ll;
long long maximumSumOfHeights(vector<int>& maxHeights) {int n = maxHeights.size();vector<ll> suffix(n);stack<int> st;ll sum = 0;for (int i = n - 1; i >= 0; i--) {while (!st.empty() && maxHeights[i] <= maxHeights[st.top()]) {int previous = st.top();st.pop();if (st.empty()) {sum -= (ll)maxHeights[previous] * (n - previous);}else {sum -= (ll)maxHeights[previous] * (st.top() - previous);}}if (st.empty()) {sum += (ll)maxHeights[i] * (n - i);}else {sum += (ll)maxHeights[i] * (st.top() - i);}suffix[i] = sum;st.push(i);}st = stack<int>();sum = 0;vector<ll> prefix(n);for (int i = 0; i < n; i++) {while (!st.empty() && maxHeights[i] <= maxHeights[st.top()]) {int previous = st.top();st.pop();if (st.empty()) {sum -= (ll)maxHeights[previous] * (previous + 1);}else {sum -= (ll)maxHeights[previous] * (previous - st.top());}}if (st.empty()) {sum += (ll)maxHeights[i] * (i + 1);}else {sum += (ll)maxHeights[i] * (i-st.top());}prefix[i] = sum;st.push(i);}ll maxSum = 0;for (int i = 0; i < n; i++) {maxSum = max(maxSum, prefix[i] + suffix[i] - maxHeights[i]);}return maxSum;
}
int main() {vector<int> maxHeights = {5, 3, 4, 1, 1};cout << maximumSumOfHeights(maxHeights);
}
100047. 统计树中的合法路径数目
题目链接
给你一棵 n 个节点的无向树,节点编号为 1 到 n 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示节点 ui 和 vi 在树中有一条边。
请你返回树中的 合法路径数目 。
如果在节点 a 到节点 b 之间 恰好有一个 节点的编号是质数,那么我们称路径 (a, b) 是 合法的 。
注意:
- 路径
(a, b)指的是一条从节点a开始到节点b结束的一个节点序列,序列中的节点 互不相同 ,且相邻节点之间在树上有一条边。 - 路径
(a, b)和路径(b, a)视为 同一条 路径,且只计入答案 一次 。 1 <= n <= 10^5edges.length == n - 1edges[i].length == 21 <= ui, vi <= n- 输入保证
edges形成一棵合法的树。
const int MAX_NUM = 1e5;
bool isNonPrime[MAX_NUM + 1]; // 非质数=true,质数=falseint initialize = []() {isNonPrime[1] = true;for (int num = 2; num * num <= MAX_NUM; num++) {if (!isNonPrime[num]) {for (int multiple = num * num; multiple <= MAX_NUM; multiple += num) {isNonPrime[multiple] = true;}}}return 0;
}();class Solution {
public:long long countPaths(int numNodes, vector<vector<int>> &edges) {// 创建邻接列表表示图的结构vector<vector<int>> adjacencyList(numNodes + 1);for (auto &edge : edges) {int node1 = edge[0], node2 = edge[1];adjacencyList[node1].push_back(node2);adjacencyList[node2].push_back(node1);}// 用于记录DFS遍历的节点vector<int> visitedNodes;// 定义DFS函数,遍历与当前节点相关的非质数节点function<void(int, int)> dfs = [&](int currentNode, int parentNode) {visitedNodes.push_back(currentNode);for (int adjacentNode : adjacencyList[currentNode]) {if (adjacentNode != parentNode && isNonPrime[adjacentNode]) {dfs(adjacentNode, currentNode);}}};// 用于记录每个节点所在子树的节点数量vector<int> subtreeSize(numNodes + 1);long long result = 0;for (int currentNode = 1; currentNode <= numNodes; currentNode++) {if (isNonPrime[currentNode]) continue; // 跳过非质数节点int nonPrimeNodesSum = 0;for (int adjacentNode : adjacencyList[currentNode]) {if (!isNonPrime[adjacentNode]) continue; //跳过质数节点if (subtreeSize[adjacentNode] == 0) {visitedNodes.clear();// 执行DFS遍历,记录子树中的节点dfs(adjacentNode, -1);for (int node : visitedNodes) {subtreeSize[node] = visitedNodes.size();}}// 计算与当前节点相关的路径数量result += (long long)subtreeSize[adjacentNode] * nonPrimeNodesSum;nonPrimeNodesSum += subtreeSize[adjacentNode];}// 加上从当前节点出发的路径数量result += nonPrimeNodesSum;}return result;}
};相关文章:

leetcode 周赛 364
参考视频: 单调栈【力扣周赛 364】 文章目录 8048. 最大二进制奇数100049. 美丽塔 I100048. 美丽塔 II100047. 统计树中的合法路径数目 8048. 最大二进制奇数 题目链接 给你一个 二进制 字符串 s ,其中至少包含一个 1 。 你必须按某种方式 重新排列 字…...
开机自启动Linux and windows
1、背景 服务器由于更新等原因重启,部署到该服务上的响应的应用需要自启动 2、Linux 2.1 方式一 编写启动应用的sh脚本授权该脚本权限 chmod 777 xxx.sh 修改rc.loacl 位置:/etc/rc.local 脚本:sh /home/xxxx.sh & 授权rc.local …...

科技云报道:大模型的阴面:无法忽视的安全隐忧
科技云报道原创。 在AI大模型的身上,竟也出现了“to be or not to be”问题。 争议是伴随着大模型的能力惊艳四座而来的,争议的核心问题在于安全。安全有两个方面,一个是大模型带来的对人类伦理的思考,一个是大模型本身带来的隐…...

2023年前端流行什么技术和框架了?
Web前端三大主流框架有React、Vue.js和Angular,由于接触过Vue.js,接下来主讲最新的Vue3.0! Vue3.0作为最新版本的Vue.js框架,拥有更强大的性能和更丰富的功能,为低代码开发平台注入了全新的活力。而JNPF快速开发平台作…...

Nginx 背锅解析漏洞
Nginx 背锅解析漏洞 文章目录 Nginx 背锅解析漏洞1 在线漏洞解读:2 环境搭建3 影响版本:4 漏洞复现4.1 访问页面4.2 上传文件 4.3 上传失败4.4 使用bp进行分析包4.5 对返回图片位置进行访问4.6 执行php代码技巧-图片后缀加./php4.7 分析原因 --》cgi.fix_pathinfo--…...

AI与传统数据库 - ChatGPT风过之后 | 从Duet AI说开来
作者:Ni Demai,是NineData数据库产品专家,曾任阿里云数据库国际产品总负责人,华为高斯 GaussDB 创始团队核心架构师,IBM Db2 资深研发工程师。 Demai 专注 Cloud-Native database 架构设计,分析型 MPP&…...

L1-032 Left-pad C++解法
一、题目再现 根据新浪微博上的消息,有一位开发者不满NPM(Node Package Manager)的做法,收回了自己的开源代码,其中包括一个叫left-pad的模块,就是这个模块把javascript里面的React/Babel干瘫痪了。这是个…...
Python 用列表实现模拟手机通讯录(简易版)
"""列表实现好友管理系统知识点:1、列表存储信息2、列表增删改查3、嵌套循环4、字符串分割和拼接(重点)5、列表索引"""# 暂存好友信息(程序结束数据删除) friend_info list()input_buf…...
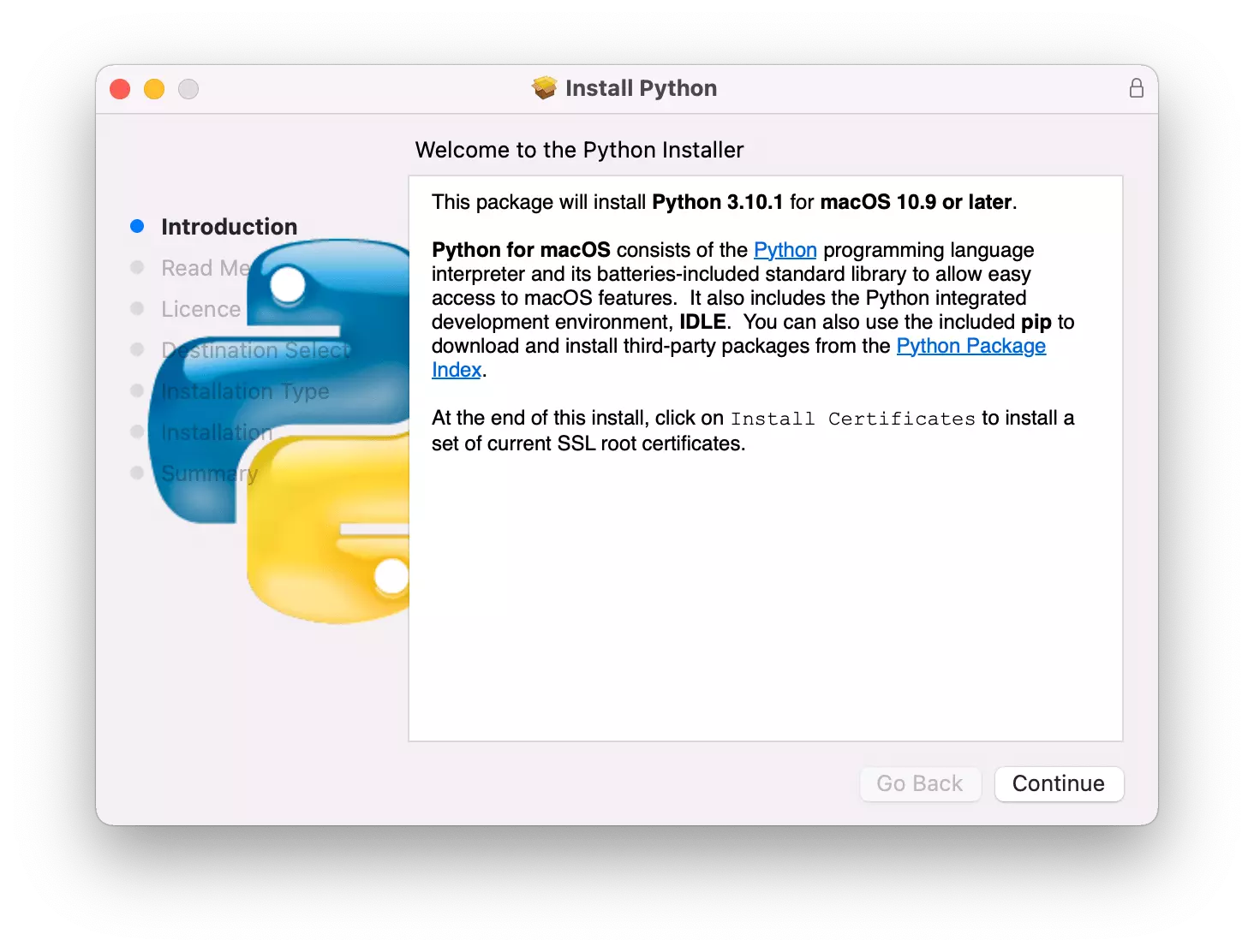
macOS使用官方安装包安装python
新手程序员可能想知道如何在 Mac 上正确安装 Python,这里介绍在 macOS 上安装 Python 的方法。 操作步骤 1.从 Python 官方网站 (python.org) 下载最新的 Python 版本. 单击 macOS 链接并选择最新的 Python 版本。 2.下载完成后,双击包开始安装Python…...
如何重装Windows Mirosoft Store
重装Windows Mirosoft Store 如何重装Windows Mirosoft Store呢?如何下载Windows Mirosoft Store呢?Windows Mirosoft Store不见了咋办?Windows 自带软件不见了咋办等等?写在前面 1.文件准备2.安装 如何重装Windows Mirosoft Stor…...

软考高级系统架构设计师系列论文真题七:基于构件的软件开发
软考高级系统架构设计师系列论文真题七:基于构件的软件开发 一、基于构件的软件开发二、找准核心论点三、理论素材准备四、精品范文赏析1.摘要2.正文3.总结软考高级系统架构设计师系列论文之:百篇软考高级架构设计师论文范文软考高级系统架构设计师系列之:论文题目类型、论文…...

git rebase 修改中间的commit
0. 前言 今天在移植最新版本 kfence 功能的时候,一共需要移植大概40多个 patch,中间有很多patch 存在冲突,需要手动修改后才能合并。当所有的patch 都合并完成进行编译的时候,发现其中一个 patch 手动合并出了个错误。 假如共有…...
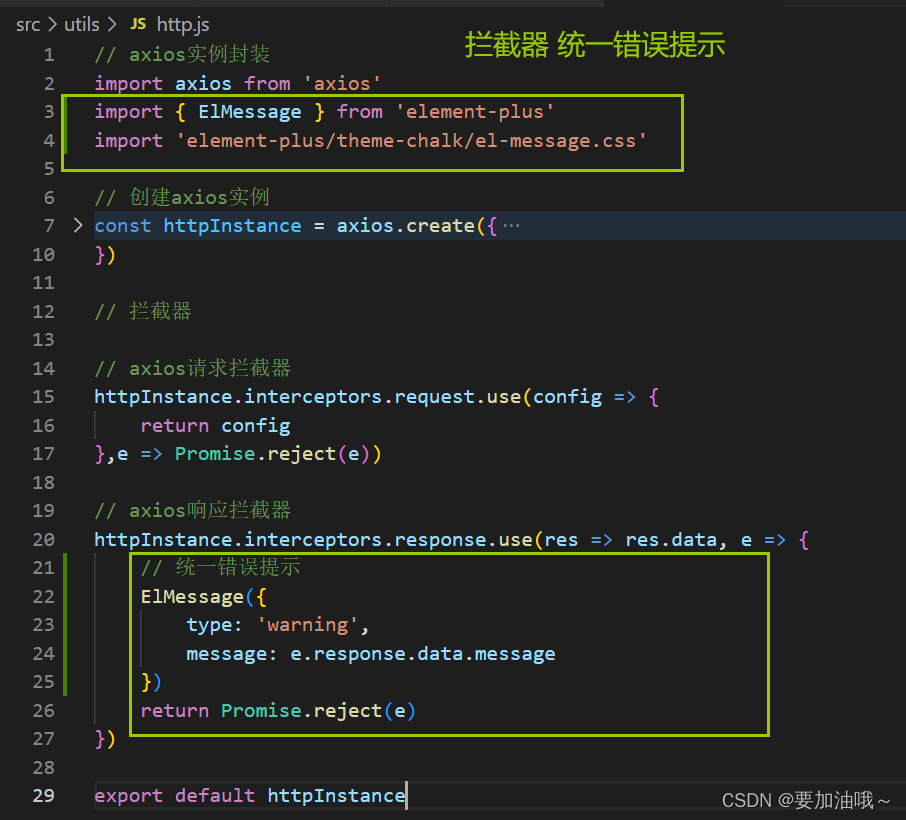
登录业务实现 - token登录鉴权
登录业务实现: 登录成功/失败实现 -> pinia管理用户数据及数据持久化 -> 不同登录状态的模板适配 -> 请求拦截器携带token(登录鉴权) -> 退出登录实现 -> token失效(401响应拦截) 1. 登录成…...

内存对齐--面试常问问题和笔试常考问题
1.内存对齐的意义 C 内存对齐的主要意义可以简练概括为以下几点: 提高访问效率:内存对齐可以使数据在内存中以更加紧凑的方式存储,从而提高了数据的访问效率。处理器通常能够更快地访问内存中对齐的数据,而不需要额外的字节偏移计…...

贪心算法-会议室问题
1、题目描述 一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目。现在给你两个长度一样的数组,starts数组代码每个会议开始的时间,ends数组代表每个会议结束的时间。 在给你一个当前时间,请你求出当日可以利用会议室宣讲的…...
单日 5000 亿行 / 900G 数据接入,TDengine 3.0 在中国地震台网中心的大型应用
小T导读:为满足地震预警数据存储、检索和处理的建设与集成需求,以及响应国家国产软件自主可控的号召,中国地震台网中心决定选用国产数据库 TDengine 来存储和处理地震波形数据。本文将针对 TDengine 3.0 在地震领域的应用展开详细讲解。 关于…...

【VIM系列】cscope命令
cscope...

Vue的自定义事件(Custom Events):实现组件间通信的强大工具
Vue的自定义事件(Custom Events):实现组件间通信的强大工具 Vue.js是一款流行的JavaScript框架,用于构建交互式的Web应用程序。在Vue中,组件是构建应用程序的基本单元,它们之间的通信对于构建复杂的应用非…...
)
简易实现通讯录(1.0)
前言 我们还是像以前一样,分为三个文件来书写,分别是contact.h,contact.c,test.c 分别用来声明函数,实现函数和测试函数功能,现在就让我们开始吧. 1.基本逻辑 首先我们定义通讯录里的数据,我们定义为结构体 typedef struct PeoInfo {char name[NAME_MAX];int age;char sex[SEX_…...

CSS笔记——触发式动画Transition、主动式动画Animation、Transfrom 动画、CSS 3D 动画、阴影和滤镜样式
CSS动画 一、触发式动画Transition transition过渡动画,一般配合伪类使用 属性值: transition-duration: 指定过渡效果的持续时间,以秒或毫秒为单位。 transition-timing-function: 指定过渡效果的时间函数ÿ…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
