CMU15-213 课程笔记 04-Floating Point
文章目录
- 浮点数如何用二进制表示
- IEEE 浮点数标准
- IEEE 浮点数实现
- IEEE 浮点数在内存里
- E = exp - bias 计算指数
- M = 1.xxx 尾数计算
- 举例:对一个浮点数进行转换
- 一些关于浮点数的计算等等
浮点数如何用二进制表示
计算机内部的浮点数不是这样存在内存里的(至少C语言不是)但我们可以这样使用二进制来表示浮点数:
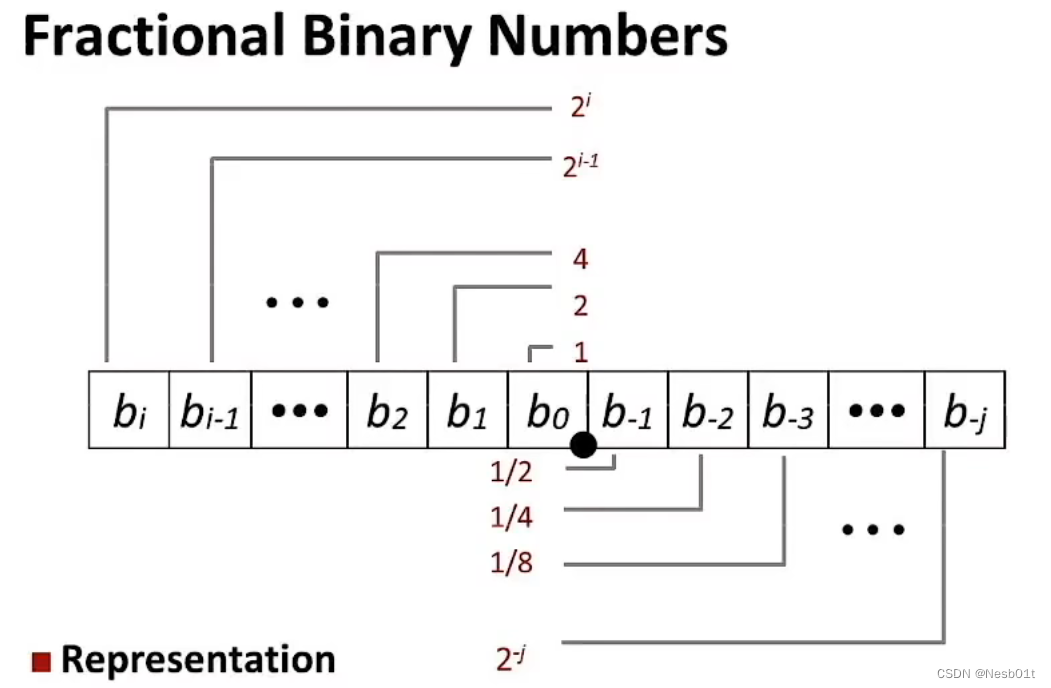
这样的表示方法有很大的局限,我们只能方便地表示 1/2,1/4 这样的数,如果要表示 1/3 之类的数字,那么只能是近似值

IEEE 浮点数标准
在1985以前,每一种计算机都可能有他自己的实现浮点数的方法,直到1985年计算机协会发布了 IEEE 754 标准,使得计算机厂商采用了一致的标准来支持浮点数

IEEE 浮点数实现
它使用一种类似科学计数法的方法来表示数字
其中:
- S 是符号位(0 或 1,用来设置是正还是负)
- M 是尾数(是一个在 1 ~ 2 之间的数字)
- 然后乘以 2 的 E 次幂(E 会以二进制幂形式用来扩大或减小 M 尾数,无论是32bits还是64bits)
所有浮点数都必须用这种方式来实现

IEEE 浮点数在内存里
32 bits 计算机中的 float:
- 1 位的 s 用来表示符号
- 8 位的 exp 指数,用来表示一种类似科学计数法的位数
- 23 位的 frac 尾数,也就是科学技术法的前半部分数值

E = exp - bias 计算指数
exp = 000…0 和 exp = 111…1 都是特殊的值,我们稍后讨论
指数 E 的值被解释为:以 偏置 biased 形式表示
所以 E 的实际值是 exp - bias
简单来说,exp 就是那个 7 位的值,把 exp 减去一个 bias 偏置值,就得到了 E 值!
对于 32 bits 的 float 浮点数来说,bias = 127,8 bits 的最高位权重是 128,128 - 1 = 127 就是 bias 了
那么 64 bits 呢?64 bits 的 exp 有 11 位,那么 11 bits 的最高权重就是 1024,1024 - 1 = 1023 就是 bias
我们此时得到了 bias = 127,接下来计算 exp 值
exp 值只需要把 除了第一位 以外 剩下的 7 位 当做二进制数字来计算就好了(这其实也是正负数补码的计算方式!)
这样做的好处是,如果要比较2个浮点数,刨去第一位以后就可以直接进行位运算比较!十分方便
- 最大的值就是 011111…1
- 最小的值就是 10000…0
M = 1.xxx 尾数计算
最小的尾数是 0000…0,此时 M = 1.0
最大的尾数是 1111…1,此时 M 超级接近 2.0
尾数就是 1.xxx 后面的 xxx,你把一堆 0 加起来当然是 0
你把一堆 1 加起来,那就是 1/2 + 1/4 + 1/8 … 最后当然是非常接近 1 的一个数
举例:对一个浮点数进行转换
多说无益,我们来举个例子,令 float F = 15213.0
经过二进制 表示,得到 15213(10进制的)= 11101101101101(二进制的)
使用科学计数法表示,得到 1.1101101101101 乘以 2的13次方
这样我们就得到了尾数 frac 和 M 的值:
- M = (去掉1.) 1101101101101
- frac = 11011011011010000000000
同时我们也得到了:
- E = 13(因为指数是13)
- Bias = 127(32 bits 的 float 就是127)
- Exp = 140(10001100,因为 Exp - Bias = 13,所以 Exp = 140)
这就是结果了,我们成功把 15213 这个十进制数,存到内存这个二进制结构里了~

一些关于浮点数的计算等等
后续关于浮点数在计算机里应用的细节内容可能会补上,暂时跳过,请看原视频~
相关文章:

CMU15-213 课程笔记 04-Floating Point
文章目录 浮点数如何用二进制表示IEEE 浮点数标准IEEE 浮点数实现IEEE 浮点数在内存里 E exp - bias 计算指数M 1.xxx 尾数计算举例:对一个浮点数进行转换一些关于浮点数的计算等等 浮点数如何用二进制表示 计算机内部的浮点数不是这样存在内存里的(至…...
DockerKubernetes ❀ Service下Port端口区分
文章目录 概述案例 概述 在Kubernetes中,Service(svc)是一种抽象机制,用于将一组 Pod 暴露给其他应用程序或服务。Service 可以有三种类型的端口: nodePort:这是 Service 在节点上公开的端口。可以使用此…...

【C++】笔试训练(一)
目录 一、选择题二、编程1、组队竞赛2、删除公共字符 一、选择题 1、以下for循环的执行次数是() for (int x 0, y 0; (y 123) && (x < 4); x);A 是无限循环 B 循环次数不定 C 4次 D 3次 答案:C 2、以下程序的运行结果是&…...
)
数据结构与算法之集合: Leetcode 349. 两个数组的交集 (Typescript版)
两个数组的交集 https://leetcode.cn/problems/intersection-of-two-arrays/description/ 描述 给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。 示例 1 输入:nums1 [1,2,…...
Unity 内存性能分析器 (Memory Profiler)
一、 安装 安装有两种方式一: add package : com.unity.memoryprofiler方式二: From Packages : Unity Registry 搜索 Memory Profiler 二、 使用 打开:Windows - > Analysis - > Memory Profiler 打开MemoryProfiler界面࿰…...

前端携带Bearer Token
前端携带Bearer Token 在前端使用 axios 发送请求时,可以通过设置请求头来携带 Bearer Token。Bearer Token 是一种常用的身份验证方式,它通常用于 OAuth2 授权流程中。 要在 axios 中携带 Bearer Token,可以通过设置 Authorization 请求头…...

leetcode 周赛 364
参考视频: 单调栈【力扣周赛 364】 文章目录 8048. 最大二进制奇数100049. 美丽塔 I100048. 美丽塔 II100047. 统计树中的合法路径数目 8048. 最大二进制奇数 题目链接 给你一个 二进制 字符串 s ,其中至少包含一个 1 。 你必须按某种方式 重新排列 字…...
开机自启动Linux and windows
1、背景 服务器由于更新等原因重启,部署到该服务上的响应的应用需要自启动 2、Linux 2.1 方式一 编写启动应用的sh脚本授权该脚本权限 chmod 777 xxx.sh 修改rc.loacl 位置:/etc/rc.local 脚本:sh /home/xxxx.sh & 授权rc.local …...

科技云报道:大模型的阴面:无法忽视的安全隐忧
科技云报道原创。 在AI大模型的身上,竟也出现了“to be or not to be”问题。 争议是伴随着大模型的能力惊艳四座而来的,争议的核心问题在于安全。安全有两个方面,一个是大模型带来的对人类伦理的思考,一个是大模型本身带来的隐…...

2023年前端流行什么技术和框架了?
Web前端三大主流框架有React、Vue.js和Angular,由于接触过Vue.js,接下来主讲最新的Vue3.0! Vue3.0作为最新版本的Vue.js框架,拥有更强大的性能和更丰富的功能,为低代码开发平台注入了全新的活力。而JNPF快速开发平台作…...

Nginx 背锅解析漏洞
Nginx 背锅解析漏洞 文章目录 Nginx 背锅解析漏洞1 在线漏洞解读:2 环境搭建3 影响版本:4 漏洞复现4.1 访问页面4.2 上传文件 4.3 上传失败4.4 使用bp进行分析包4.5 对返回图片位置进行访问4.6 执行php代码技巧-图片后缀加./php4.7 分析原因 --》cgi.fix_pathinfo--…...

AI与传统数据库 - ChatGPT风过之后 | 从Duet AI说开来
作者:Ni Demai,是NineData数据库产品专家,曾任阿里云数据库国际产品总负责人,华为高斯 GaussDB 创始团队核心架构师,IBM Db2 资深研发工程师。 Demai 专注 Cloud-Native database 架构设计,分析型 MPP&…...

L1-032 Left-pad C++解法
一、题目再现 根据新浪微博上的消息,有一位开发者不满NPM(Node Package Manager)的做法,收回了自己的开源代码,其中包括一个叫left-pad的模块,就是这个模块把javascript里面的React/Babel干瘫痪了。这是个…...
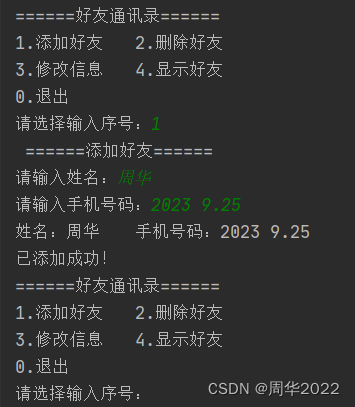
Python 用列表实现模拟手机通讯录(简易版)
"""列表实现好友管理系统知识点:1、列表存储信息2、列表增删改查3、嵌套循环4、字符串分割和拼接(重点)5、列表索引"""# 暂存好友信息(程序结束数据删除) friend_info list()input_buf…...
macOS使用官方安装包安装python
新手程序员可能想知道如何在 Mac 上正确安装 Python,这里介绍在 macOS 上安装 Python 的方法。 操作步骤 1.从 Python 官方网站 (python.org) 下载最新的 Python 版本. 单击 macOS 链接并选择最新的 Python 版本。 2.下载完成后,双击包开始安装Python…...
如何重装Windows Mirosoft Store
重装Windows Mirosoft Store 如何重装Windows Mirosoft Store呢?如何下载Windows Mirosoft Store呢?Windows Mirosoft Store不见了咋办?Windows 自带软件不见了咋办等等?写在前面 1.文件准备2.安装 如何重装Windows Mirosoft Stor…...

软考高级系统架构设计师系列论文真题七:基于构件的软件开发
软考高级系统架构设计师系列论文真题七:基于构件的软件开发 一、基于构件的软件开发二、找准核心论点三、理论素材准备四、精品范文赏析1.摘要2.正文3.总结软考高级系统架构设计师系列论文之:百篇软考高级架构设计师论文范文软考高级系统架构设计师系列之:论文题目类型、论文…...

git rebase 修改中间的commit
0. 前言 今天在移植最新版本 kfence 功能的时候,一共需要移植大概40多个 patch,中间有很多patch 存在冲突,需要手动修改后才能合并。当所有的patch 都合并完成进行编译的时候,发现其中一个 patch 手动合并出了个错误。 假如共有…...
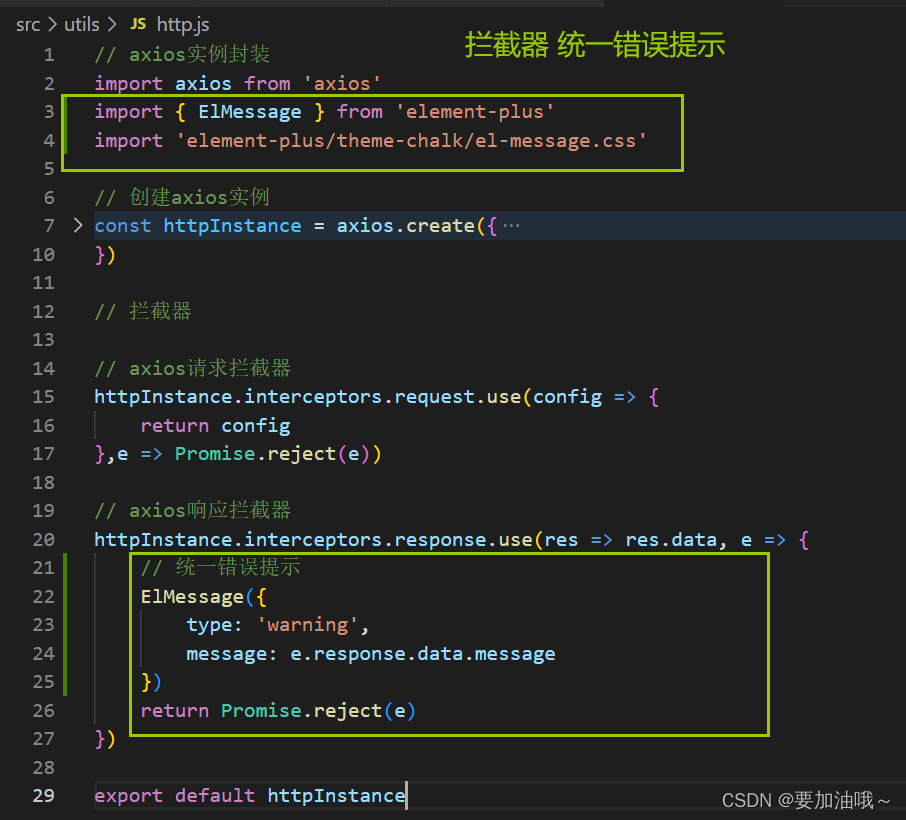
登录业务实现 - token登录鉴权
登录业务实现: 登录成功/失败实现 -> pinia管理用户数据及数据持久化 -> 不同登录状态的模板适配 -> 请求拦截器携带token(登录鉴权) -> 退出登录实现 -> token失效(401响应拦截) 1. 登录成…...

内存对齐--面试常问问题和笔试常考问题
1.内存对齐的意义 C 内存对齐的主要意义可以简练概括为以下几点: 提高访问效率:内存对齐可以使数据在内存中以更加紧凑的方式存储,从而提高了数据的访问效率。处理器通常能够更快地访问内存中对齐的数据,而不需要额外的字节偏移计…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...
