机器学习西瓜书+南瓜书吃瓜教程第三章学习笔记
本次学习为周老师的机器学习西瓜书+谢老师南瓜书+Datawhale视频
视频地址
下面为本人的学习笔记,最近很忙还没学多少,之后补!!!
u1s1,边看视频边自己手推一遍真的清楚很多,强烈推荐自己手推虽然花时间,但真的很有用很清晰
线性模型
- 1、基本形式
- 2、最小二乘估计&&极大似然估计
- 3、求解w和b
- 4、举例
机器学习是想要通过现有的数据,找到隐藏在事物背后的规律。
而大部分规律是符合线性模型的形式
为了能进行数学运算,样本中的非数值类属性都需要进行数值化。
机器学习三要素:
1.模型:根据具体问题,确定假设空间
2.策略:根据评价标准,确定选取最优模型的策略(通常会产出一个“损失函数”)
3.算法:求解损失函数,确定最优模型
1、基本形式
给定由d个属性描述的示例
其中xi是x在第i个属性上的取值,线性模型试图学的一个通过属性的线性组合来进行预测的函数,即: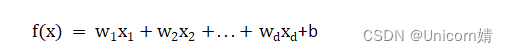
一般用向量形式写成

其中w = (w1;w2;…;wd),模型就得以确定。
2、最小二乘估计&&极大似然估计

极大似然估计的直观想法:使得观测样本出现概率最大的分布就是待求分布,也就是使得联合概率(似然函数)L( θ \theta θ )取得最大值的 θ \theta θ 即为 θ \theta θ 的估计值。

3、求解w和b
凸集介绍:向下凹的函数叫凸函数,相当于数学里面最优化的思路

梯度:多元函数的一阶导数

列向量为分母布局,行向量为分子布局。求梯度即为求偏导数。
Hessian(海塞)矩阵(多元函数的二阶导数):

其本质上是一个多元函数求最值点的问题,更具体点是凸函数求最值的问题
推导思路:
1、证明 E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 E\left( w,b\right) =\sum ^{m}_{i=1}\left( y_{i}-wx_{i}-b\right) ^{2} E(w,b)=∑i=1m(yi−wxi−b)2是关于w和b的凸函数。
2、用凸函数求最值的思路求解出w和b。

半正定矩阵的判定定理之一:
若实对称矩阵的所有顺序主子式均为非负,则该矩阵为半正定矩阵。

好的到这里我们已经完成了第一步证明,接下来我们要完成第二步证明即用凸函数求最值的思路求解出w和b。

这边手写忘拍照啦,就写一下思路吧~
首先令对b的一阶导等于0,可以求出b,为了后续求解方便首先将b化简,再对令的一阶导等于0,然后把b代进去算…
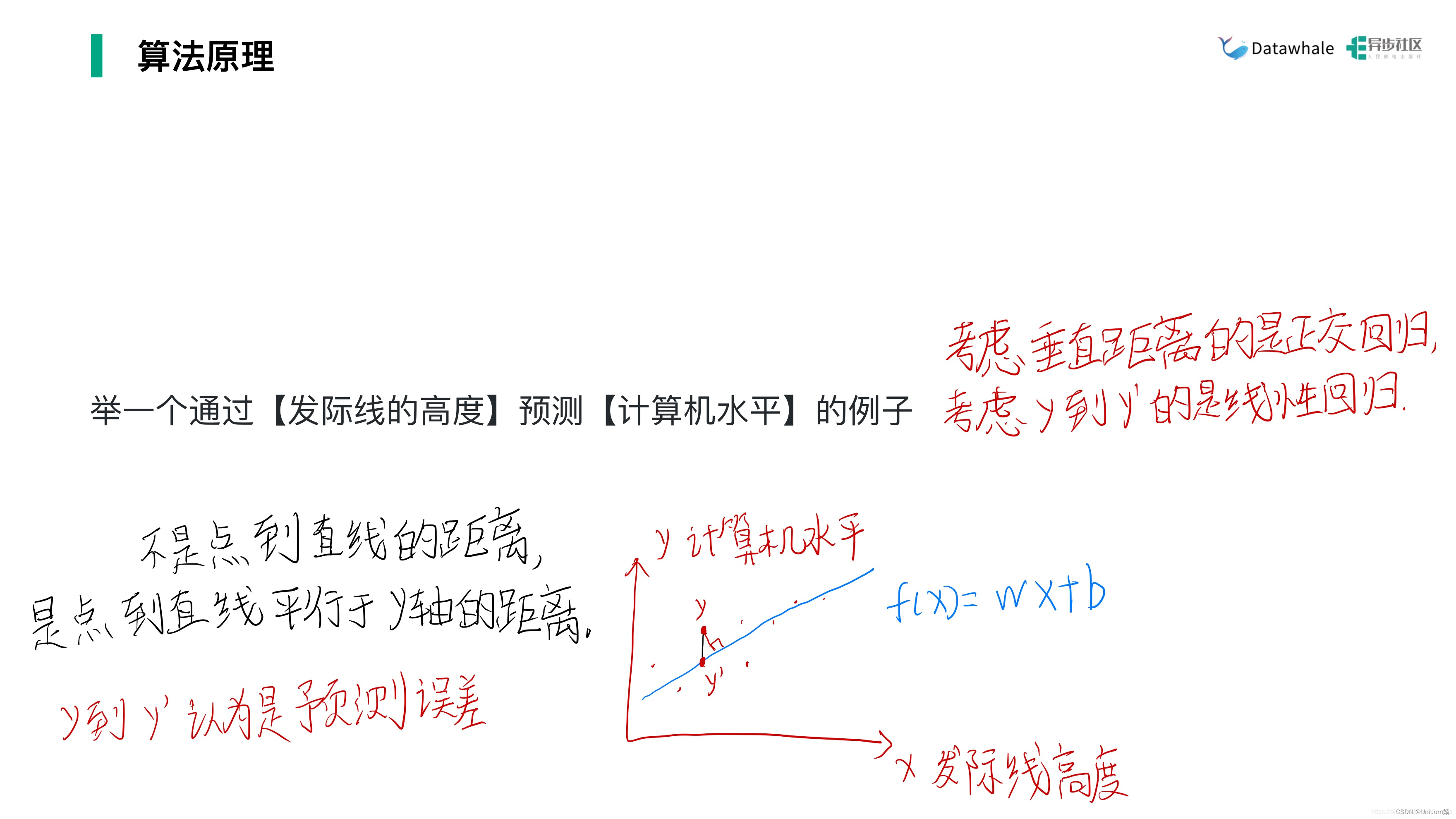
从几何的角度,让全体训练样本经过投影后:
- 异类样本的中心尽可能远
- 同类样本的方差尽可能小
对数几率回归算法的机器学习三要素:
1.模型:线性模型,
输出值的范围为,近似阶跃的单调可微函数
2.策略:
极大似然估计,信息论
3.算法:
梯度下降,牛顿法
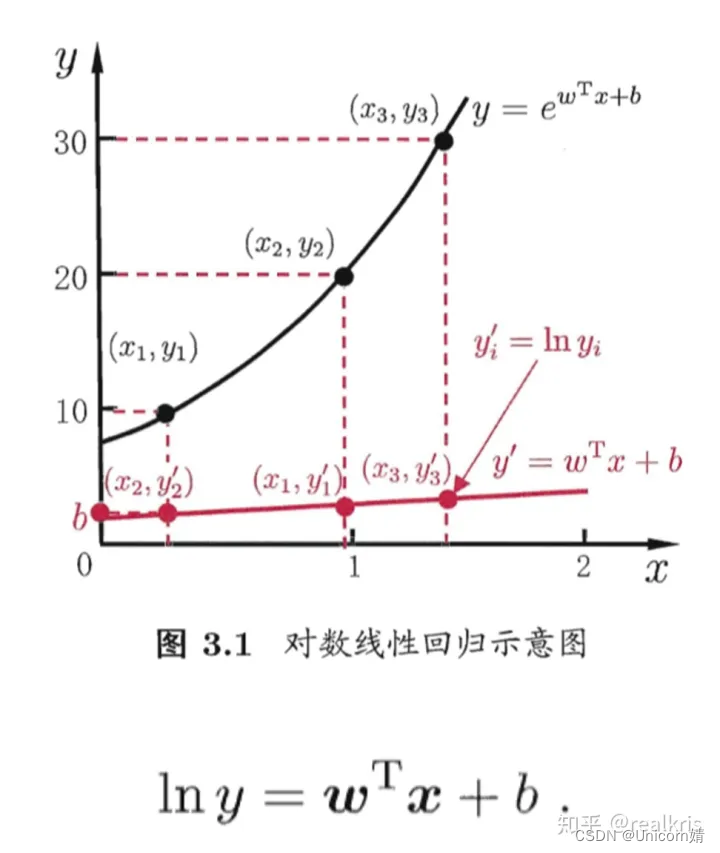
它实际是让ewTx+b逼近y,虽然形式上是线性回归,但是实际是求取输入空间到输出空间的非线性函数映射。这里的对数函数起到了将线性回归模型的预测值与真实标记相联系的作用。
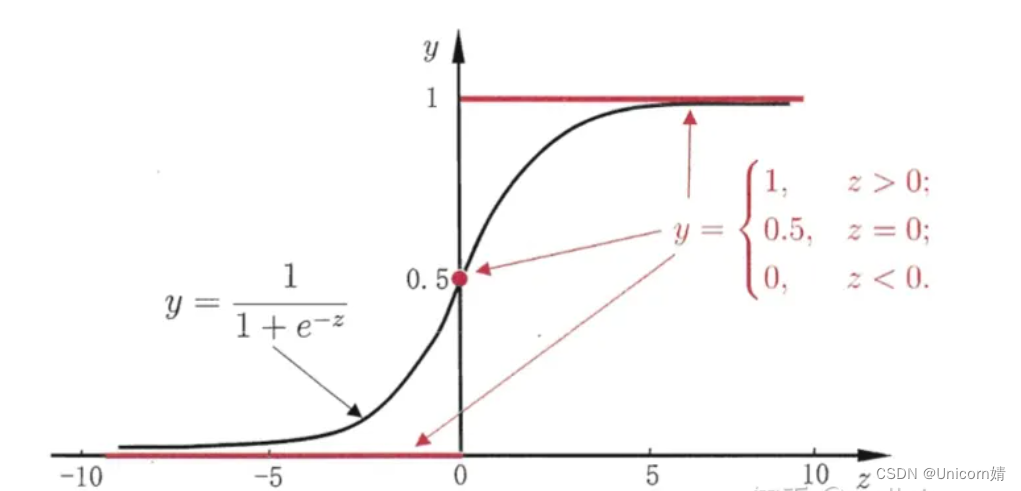
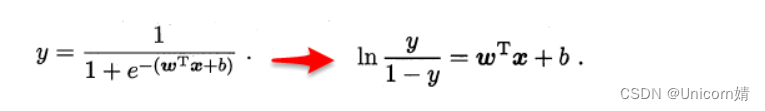
若将y视为x为正例的可能性,1-y为其为反例的可能性,两者的比值为x为正例的相对可能性。对于几率取对数得到的就是“对数几率”。对数几率回归也叫逻辑回归。
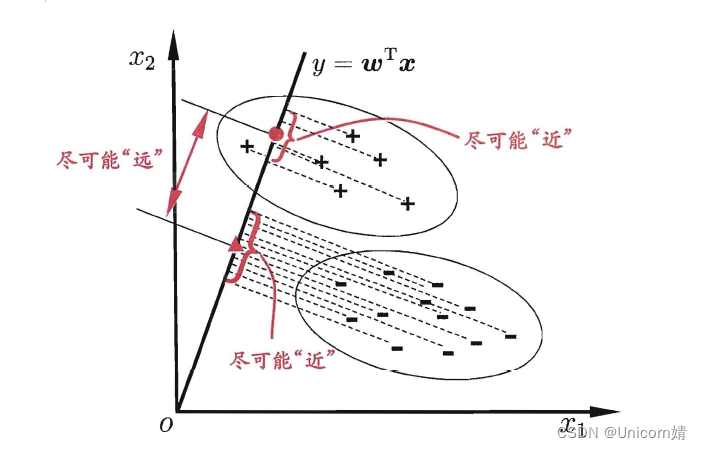
线性判别分析(Linear Discriminant Analysis,简称LDA),其基本思想是:将训练样本投影到一条直线上,使得同类的样例尽可能近,不同类的样例尽可能远。如图所示:

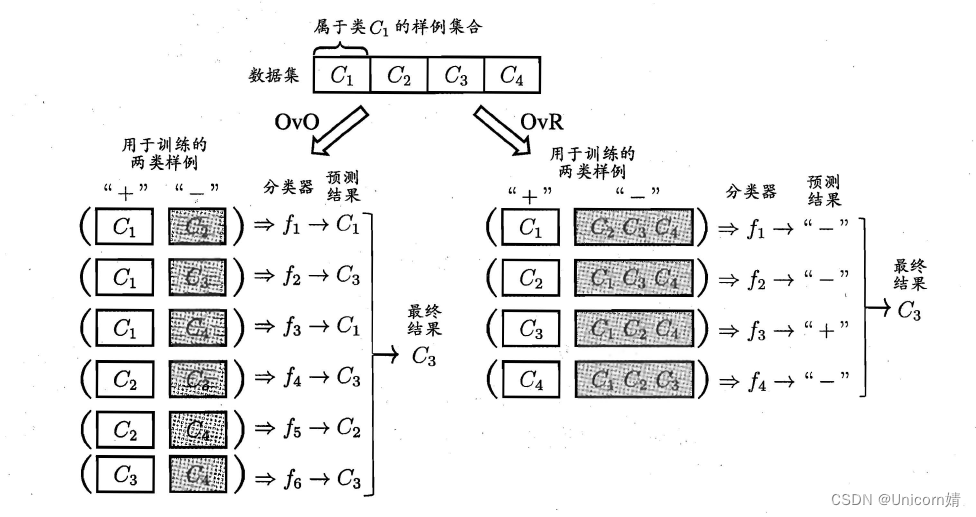
现实中我们经常遇到不只两个类别的分类问题,即多分类问题,在这种情形下,我们常常运用“拆分”的策略,通过多个二分类学习器来解决多分类问题,即将多分类问题拆解为多个二分类问题,训练出多个二分类学习器,最后将多个分类结果进行集成得出结论。最为经典的拆分策略有三种:“一对一”(OvO)、“一对其余”(OvR)和“多对多”(MvM),核心思想与示意图如下所示。
👉基于一些基本策略,利用二分类学习器来解决多分类问题
·“一对一”(One vs.One,简称OvO)
·“一对其余”(One vs.Rest,简称OvR)
·“多对多”(Many vs.Many,简称MvM)
OvO:给定数据集D,假定其中有N个真实类别,将这N个类别进行两两配对(一个正类/一个反类),从而产生N(N-1)/2个二分类学习器,在测试阶段,将新样本放入所有的二分类学习器中测试,得出N(N-1)个结果,最终通过投票产生最终的分类结果。
OvM:给定数据集D,假定其中有N个真实类别,每次取出一个类作为正类,剩余的所有类别作为一个新的反类,从而产生N个二分类学习器,在测试阶段,得出N个结果,若仅有一个学习器预测为正类,则对应的类标作为最终分类结果。
MvM:给定数据集D,假定其中有N个真实类别,每次取若干个类作为正类,若干个类作为反类(通过ECOC码给出,编码),若进行了M次划分,则生成了M个二分类学习器,在测试阶段(解码),得出M个结果组成一个新的码,最终通过计算海明/欧式距离选择距离最小的类别作为最终分类结果。
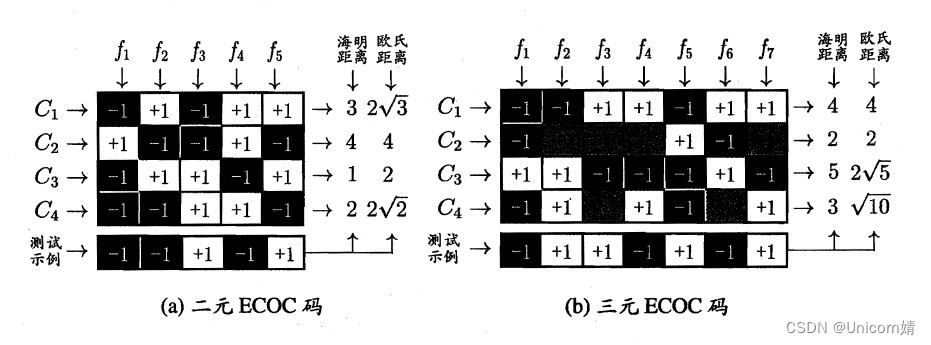
类别不平衡(class-imbanlance)就是指分类问题中不同类别的训练样本相差悬殊的情况,例如正例有900个,而反例只有100个,这个时候我们就需要进行相应的处理来平衡这个问题。常见的做法有三种:
- 在训练样本较多的类别中进行“欠采样”(undersampling),比如从正例中采出100个,常见的算法有:EasyEnsemble。
- 在训练样本较少的类别中进行“过采样”(oversampling),例如通过对反例中的数据进行插值,来产生额外的反例,常见的算法有SMOTE。
- 直接基于原数据集进行学习,对预测值进行“再缩放”处理。其中再缩放也是代价敏感学习的基础。
欠采样:去除一些反例使得正、反例数目接近
·过采样:增加一些正例使得正、反例数目接近
·阈值移动:直接基于原始数据集进行学习,但是预测时改变预测为正例的阈值(不再为0.5)
4、举例
1、sklearn中的线性回归
sklearn中的线性回归模型如下:
from sklearn.linear_model import LinearRegression
sklearn.learn_model.LinearRegression()
它表示最小二乘线性回归,线性回归拟合具有系数w = (w1,…,wp)的线性模型,以最小化数据集中观察到的目标与通过线性近似预测的目标之间的残差平方和,它的完整参数如下:
sklearn.linear_model.LinearRegression(fit_intercept=True,normalize=False,copy_X=True)
参数解释:
-
fit_intercept,是否计算此模型的截距,默认True,如果设置为False,则不会在计算中使用截距
-
normalize:数据标准化,默认为False,官方给的建议是用StandardScaler,
-
copy_X:如果为True,则X将被复制;否则,它可能会被覆盖、默认为True。
参数解释: -
fit(X,y[,sanmple_weight]):拟合线性模型(也可以叫做训练线性模型)
-
predict(X):使用线性模型进行预测。
-
score(X,y[,sample_weight]):返回预测的确定系数,即R^2.
2、案例实现:价格预测
假设有例子,x和y分别表示某面积和总价,需要根据面积来预测总价。
第一步导入模块:
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
第二步:导入数据并绘制散点图
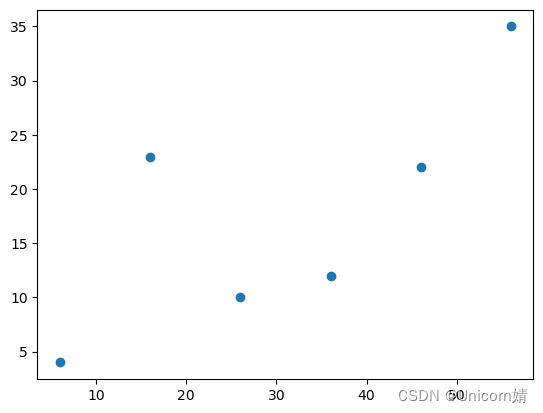
#创建数据
x = np.array([6,16,26,36,46,56]).reshape((-1,1))
y = np.array([4,23,10,12,22,35])plt.scatter(x,y)#绘制散点图
plt.show()
第三步:创建模型并拟合
model = LinearRegression().fit(x,y)
第四步:评估模型
r_sq = model.score(x,y)
print('确定系数:',r_sq)
确定系数: 0.5417910447761195
第五步:获取线性回归模型中的参数
#打印截距
print('截距:',model.intercept_)#打印斜率
print('斜率:',model.coef_)#预测一个响应并打印它:
y_pred = model.predict(x)
print('预测结果:',y_pred,sep='\n')
截距: 4.026666666666664
斜率: [0.44]
预测结果:
[ 6.66666667 11.06666667 15.46666667 19.86666667 24.26666667 28.66666667]
3、销售预测
数据集如下:
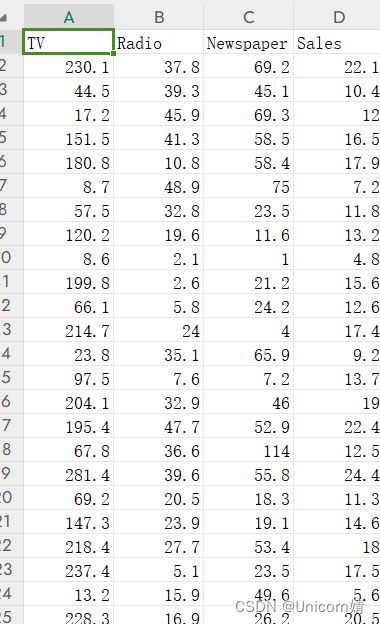
分别表示:
- TV:电视台
- Radio:广播
- Newspaper: 报纸
- sales: 销售价格
第一步:读取数据并展示数据
import pandas as pd
data=pd.read_csv(r"D:\advertising.csv")
data
如图:
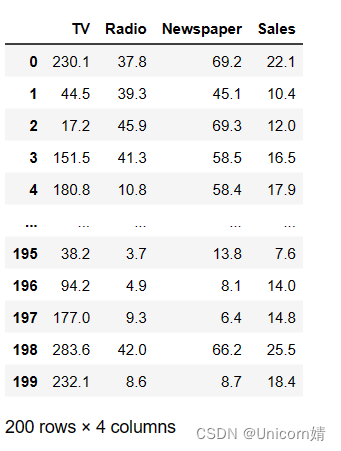
回归方程别忘了:y = c+m1x1+m2x2+…+mn*xn
- y是预测值,是因变量
- c是截距
- m1是第一个特征
- m2是第二个特征
- m3是第三个特征
- mn是第n个特征
在这里我们只做电视和销售的关系,因此方程为:y = c+m1xTV
第二步:提取自变量和因变量
X = data['TV'].values.reshape(-1,1)#使其成为数组
y = data['Sales'].values
第三步:分隔训练集和测试集。将70%的数据保留在训练数据集中,其余30%保留在测试数据集中。
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,train_size=0.7,test_size=0.3,random_state=100)
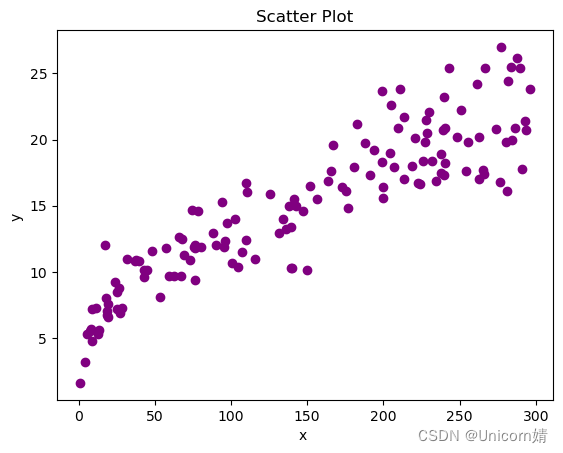
第四步:数据可视化
plt.scatter(X_train,y_train,color='purple')
plt.xlabel('x ')
plt.ylabel('y ')
plt.title("Scatter Plot")
plt.show()
如图:
第五步:建立线性回归模型
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
第六步:训练模型并使用选项回归模型预测
lr.fit(X_train,y_train)
y_predict = lr.predict(X_test)
第七步:评估模型 使用训练精确度和测试精确度。可以根据这两个指标判断是否过拟合还是欠拟合,训练精度大于测试精度则过拟合,如果两者都很小就是欠拟合。
print(f'Training accuracy:{round(lr.score(X_train,y_train)*100,2)}%')
print(f'Testing accuracy:{round(lr.score(X_test,y_test)*100,2)}%')
输出:
Training accuracy:81.58%
Testing accuracy:79.21%
4、线性回归优缺点
优点:
- 建模速度快,不需要很复杂的计算,在数据量大的情况下依然运行速度很快。
- 可以根据系数给出每个变量的理解和解释。
缺点:
不能很好地拟合非线性数据,所以需要先判断变量之间是否为线性关系。
南瓜书地址
相关文章:

机器学习西瓜书+南瓜书吃瓜教程第三章学习笔记
本次学习为周老师的机器学习西瓜书谢老师南瓜书Datawhale视频 视频地址 下面为本人的学习笔记,最近很忙还没学多少,之后补!!! u1s1,边看视频边自己手推一遍真的清楚很多,强烈推荐自己手推虽然花…...
JUnit5单元测试提示“Not tests were found”错误
JUnit5单元测试提示“Not tests were found”错误,如下图所示: 或者 问题解析: 1)使用Test注解时,不能有返回值; 2)使用Test注解时,不能使用private关键字; 存在以上情…...
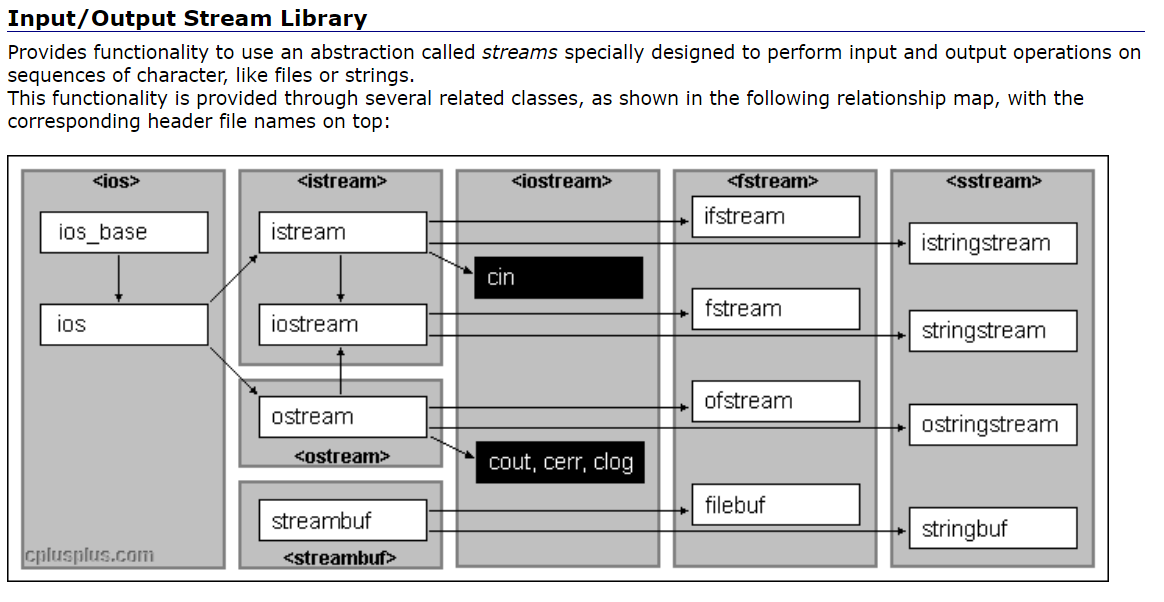
C++ -- IO流
目录 C语言的输入与输出 CIO流 C标准IO流 C文件IO流 文件常见的打开方式如下 以二进制的形式操作文件 以文本的形式操作文件 读写结构体 stringstream的简单介绍 C语言的输入与输出 C语言中我们用到的最频繁的输入输出方式就是scanf ()与printf()。 scanf(): 从标准输…...
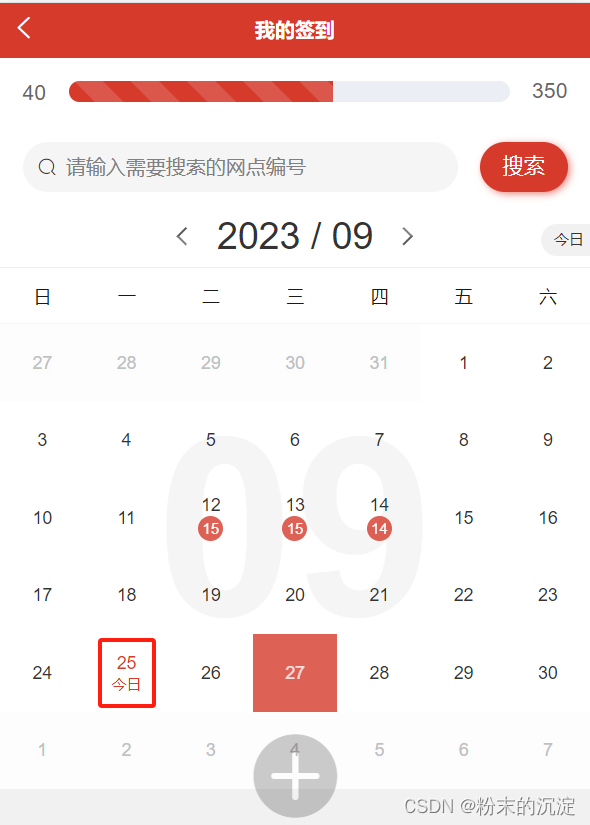
uniapp:如何修改组件默认样式
日历组件默认样式如下图,但是我不想要右上角的红点,并且日期下面的数字要加红色背景,变成圆形,还是先用元素检查找到元素的类名,然后通过/deep/来覆盖样式,需要注意的是,lang要scss或者less&…...
 导致 FastJson parsObject()对父类属性失效)
Lombok @Accessors(chain = true) 导致 FastJson parsObject()对父类属性失效
我们在项目中经常会用到lombok工具对POJO类进行简化,但不可避免的存在父类和子类的设计,并且会对父类和子类进行序列化和反序列化,今天遇到了一个问题,序列化的json字符串转化为子类对象时无法获取到父类属性值,对象中所有父类属性均为空值或默认值,很是奇怪,代码如下: 父类:P…...
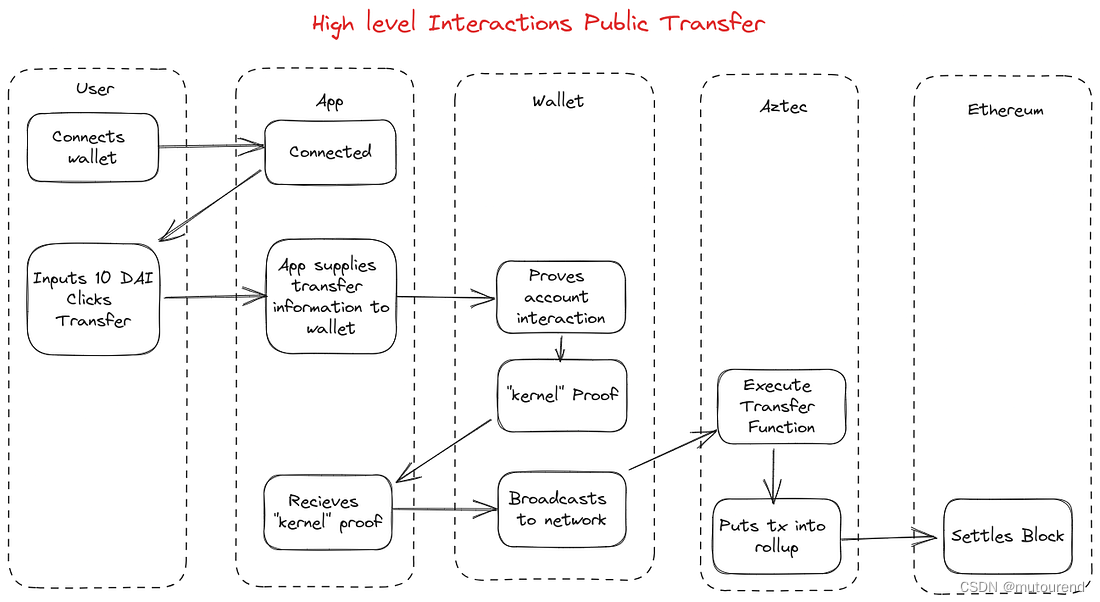
Aztec交易架构解析
1. 引言 前序博客有: Aztec的隐私抽象:在尊重EVM合约开发习惯的情况下实现智能合约隐私完全保密的以太坊交易:Aztec网络的隐私架构Aztec.nr:Aztec的隐私智能合约框架——用Noir扩展智能合约功能Account Abstraction账号抽象——…...
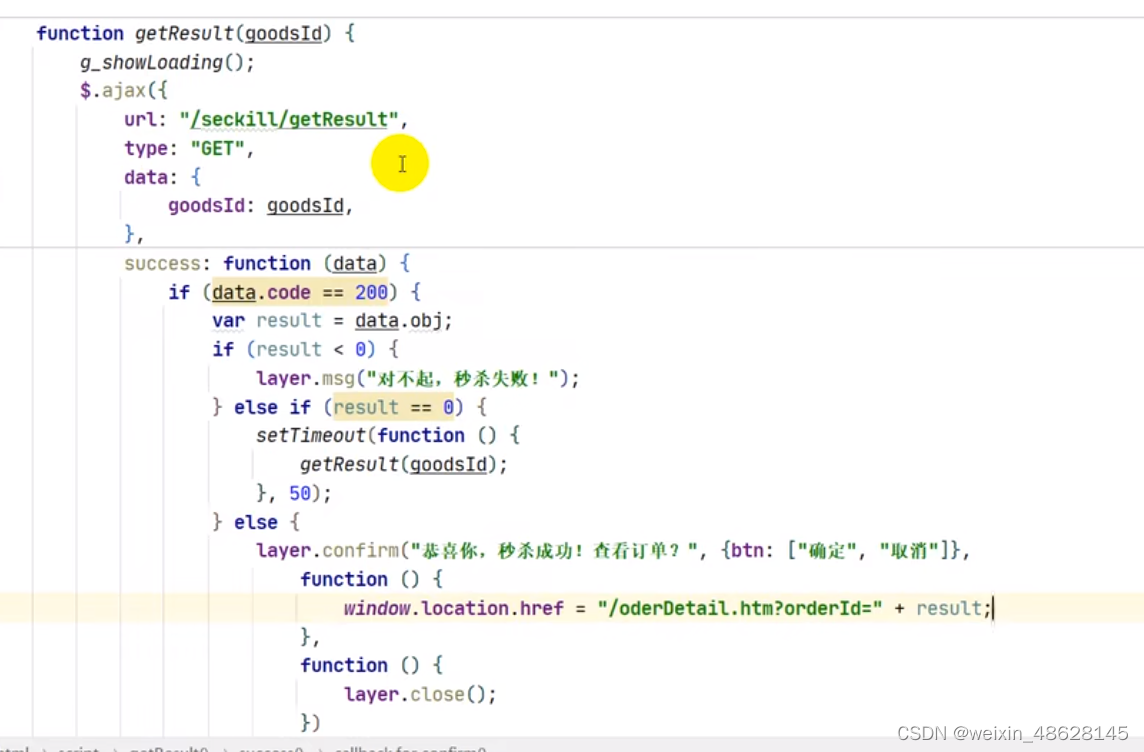
商品秒杀系统整理
1、使用redis缓存商品信息 2、互斥锁解决缓存击穿问题,用缓存空值解决缓存穿透问题。 3、CAS乐观锁解决秒杀超卖的问题 4、使用redission实现一人一单。(分布式锁lua)脚本。 5、使用lua脚本进行秒杀资格判断(将库存和用户下单…...

C语言实现八种功能的通讯录(添加、删除、查找、修改、显示、排序、退出、清空)
通讯录功能概要及前提说明 此通讯录利用C语言完成,可以实现八种功能的通讯录(添加、删除、查找、修改、显示、排序、退出、清空) 代码由三部分组成,为什么要写成三部分而不写成一部分可以参考我以前的博客,如下&…...

视频监控/视频汇聚/安防视频监控平台EasyCVR配置集群后有一台显示离线是什么原因?
开源EasyDarwin视频监控TSINGSEE青犀视频平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,TSINGSEE青犀视频安防监控汇聚平台可支持1、4、9、16个画面窗口播放,可同时播放多…...
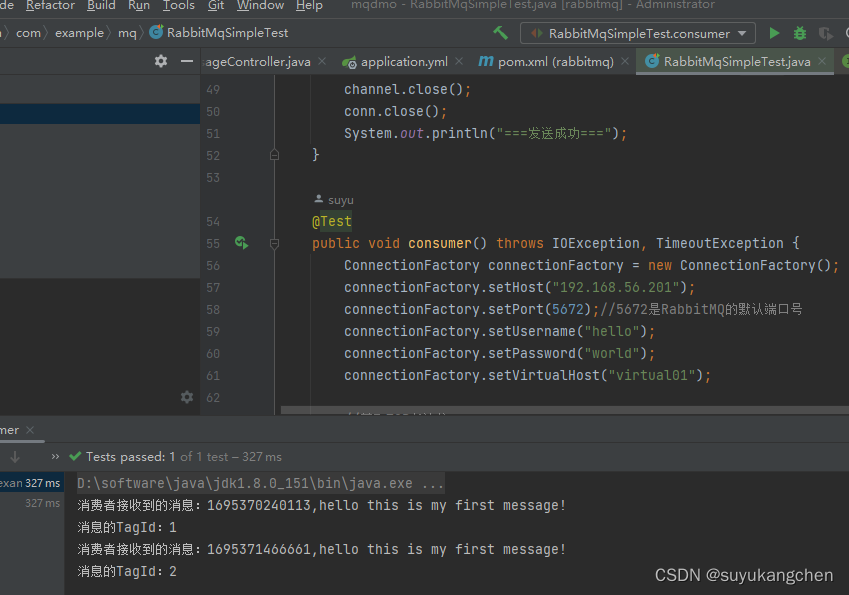
【RabbitMQ实战】02 生产者和消费者示例
在上一节中,我们使用docker部署了RabbitMQ,这一节我们将写一段生产者和消费者的代码。将用到rabbitmq的原生API来进行生产和发送消息。 一、准备工作 开始前,我们先在RabbitMQ控制台建相好关的数据 本机的RabbitMQ部署机器是192.168.56.201…...
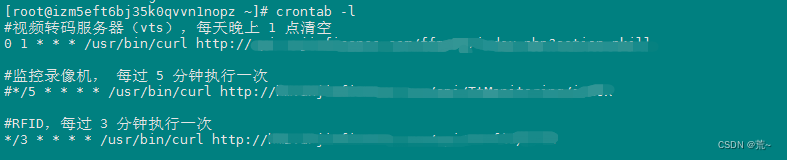
Linux下ThinkPHP5实现定时器任务 - 结合crontab
实例一: 1.在/application/command创建要配置的PHP类文件,需要继承Command类,并重写configure和execute两个方法,例如: <?php namespace app\command; use think\console\Command; use think\console\Input; use think\cons…...
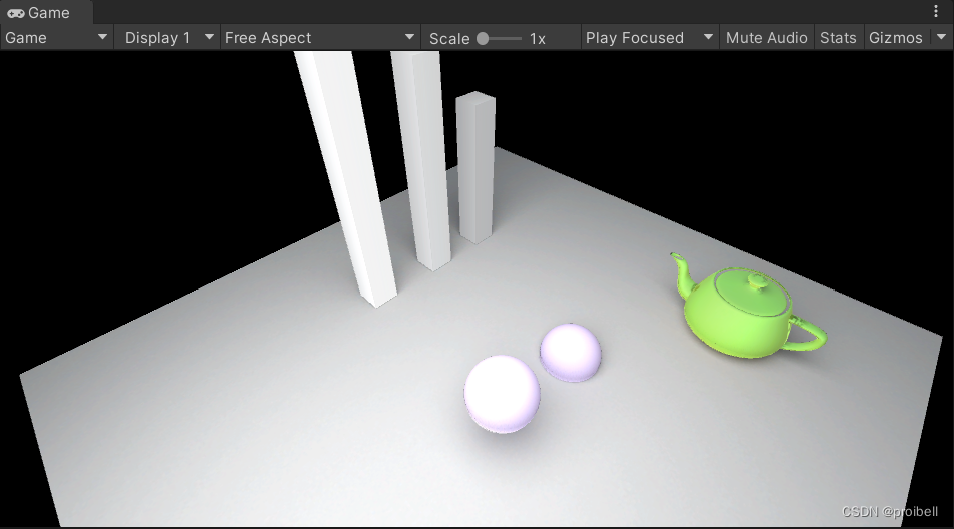
3dsmax模型烘焙光照贴图并导入unity流程详解
目录 前言 软件环境 前置知识储备 一、模型场景搭建 二、模型材质处理 三、vray渲染准备 四、烘焙至贴图 五、unity场景准备 六、贴图与材质 前言 该流程针对某些固定场景(模型发布、无法使用实时渲染引擎等)情况下的展示,本文记录烘…...
安卓生成公钥和md5签名
安卓公钥和md5证书签名 大家好,最近需要备案app,用到了公钥和md5,MD5签名我倒是知道,然而对于公钥却一下子不知道了, 现在我讲一下我的流程。 首先是md5证书签名的查看, 生成了apk和签名.jks后&…...

pwndbg安装(gdb插件)
pwndbg安装(gdb插件) 源地址:https://github.com/pwndbg/pwndbg 手动安装 git clone https://github.com/pwndbg/pwndbg cd pwndbg ./setup.sh 没啥问题运行gdb的话就可以看到明显的不同了 如果安装成功了,但没有生效 如果有问…...

SpringBoot 学习(二)配置
2. SpringBoot 配置 2.1 配置文件类型 配置文件用于修改 SpringBoot 的默认配置。 2.1.1 properties 文件 **properties ** 是属性文件后缀。 文件名:application.properties 只能保存键值对。 基础语法:keyvalue namewhy注入配置类 Component //…...

西门子828d授权密钥破解经验分享 I7I54833762
操作数组的方法 Array.prototype.toSorted(compareFn) //返回一个新数组,其中元素按升序排序,而不改变原始数组。 Array.prototype.toReversed() //返回一个新数组,该数组的元素顺序被反转,但不改变原始数组。 Array.prototype.to…...

06贪心:跳跃游戏
06贪心:跳跃游戏 55. 跳跃游戏 刚看到本题一开始可能想:当前位置元素如果是 3,我究竟是跳一步呢,还是两步呢,还是三步呢,究竟跳几步才是最优呢? 其实跳几步无所谓,关键在于可跳的…...

鄙视测试,理解测试,成为测试
首先,其实题主的问题还是很实诚的,我刚开始做测试的时候其实也是这个心态,想转开发,也学习了很多的语言,个人觉得这是职业危机感的表现,挺好的,也相信题主不管去做开发和测试都会去不断的学习和…...
MySQL数据库基础知识要点总结
目录 前言 一.数据库构成 1.1 表 1.2 关系 1.3 索引 1.4 查询语言 1.5 数据库管理系统 二.数据类型 2.1 整数 2.2 浮点 2.3 日期与时间 2.4 字符串 三.约束条件 3.1 主键约束 3.2 唯一约束 3.3 外键约束 3.4 非空约束 3.5 默认值约束 总结 前言 数据库是…...
基础运维(一)YUM仓库
一 自定义YUM仓库 1 Yum仓库特点 作为yum源需要准备的内容 大量的rpm 软件安装包文件针对这些软件包的 repodata/ 仓库档案 repodata/ 仓库档案数据 filelists.xml.gz // 软件包的文件安装清单primary.xml.gz // 软件包的基本/主要信息other.xml.gz // 软件包…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
