《动手学深度学习 Pytorch版》 7.5 批量规范化
7.5.1 训练深层网络
训练神经网络的实际问题:
-
数据预处理的方式会对最终结果产生巨大影响。
-
训练时,多层感知机的中间层变量可能具有更广的变化范围。
-
更深层的网络很复杂容易过拟合。
批量规范化对小批量的大小有要求,只有批量大小足够大时批量规范化才是有效的。
用 x ∈ B \boldsymbol{x}\in B x∈B 表示一个来自小批量 B B B 的输入;$\hat{\boldsymbol{\mu}}_B $ 表示小批量 B B B 的样本均值; σ ^ B \hat{\boldsymbol{\sigma}}_B σ^B 表示小批量 B B B 的样本标准差;批量规范化 BN 根据以下表达式转换 x \boldsymbol{x} x:
B N ( x ) = γ ⊙ x + μ ^ B σ ^ B + β BN(\boldsymbol{x})=\gamma\odot\frac{\boldsymbol{x}+\hat{\boldsymbol{\mu}}_B}{\hat{\boldsymbol{\sigma}}_B}+\beta BN(x)=γ⊙σ^Bx+μ^B+β
应用标准化后生成的小批量的均值为 0,单位方差为 1。此外,其中还包含与 x \boldsymbol{x} x 形状相同的拉伸参数 γ \gamma γ 和偏移参数 β \beta β。需要注意的是, γ \gamma γ 和 β \beta β 是需要与其他模型一起参与学习的参数。
从形式上看,可以计算出上式中的 $\hat{\boldsymbol{\mu}}_B $ 和 σ ^ B \hat{\boldsymbol{\sigma}}_B σ^B:
μ ^ B = 1 ∣ B ∣ ∑ x ∈ B x σ ^ B = 1 ∣ B ∣ ∑ x ∈ B ( x − μ ^ B ) 2 + ϵ \begin{align} \hat{\boldsymbol{\mu}}_B &= \frac{1}{\left|B\right|}\sum_{\boldsymbol{x}\in B}\boldsymbol{x}\\ \hat{\boldsymbol{\sigma}}_B &= \frac{1}{\left|B\right|}\sum_{\boldsymbol{x}\in B}(\boldsymbol{x}-\hat{\boldsymbol{\mu}}_B)^2+\epsilon \end{align} μ^Bσ^B=∣B∣1x∈B∑x=∣B∣1x∈B∑(x−μ^B)2+ϵ
式中添加的大于零的常量 ϵ \epsilon ϵ 可以保证不会发生除数为零的错误。
7.5.2 批量规范化层
全连接层和卷积层需要两种略有不同的批量规范化策略:
-
全连接层
通常,我们将批量规范化层置于全连接层中的仿射变换和激活函数之间。 设全连接层的输入为 x x x,权重参数和偏置参数分别为 W \boldsymbol{W} W 和 b b b,激活函数为 ϕ \phi ϕ,批量规范化的运算符为 B N BN BN。那么,使用批量规范化的全连接层的输出的计算详情如下:
h = ϕ ( B N ( W x + b ) ) \boldsymbol{h}=\phi(BN(\boldsymbol{W}x+b)) h=ϕ(BN(Wx+b))
-
卷积层
对于卷积层,可以在卷积层之后和非线性激活函数之前应用批量规范化。而且需要对多个输出通道中的每个输出执行批量规范化,每个通道都有自己的标量参数:拉伸和偏移参数。
-
预测过程中的批量规范化
批量规范化在训练模式和预测模式下的行为通常不同。
7.5.3 从零实现
import torch
from torch import nn
from d2l import torch as d2l
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):if not torch.is_grad_enabled(): # 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)else:assert len(X.shape) in (2, 4)if len(X.shape) == 2: # 使用全连接层的情况,计算特征维上的均值和方差mean = X.mean(dim=0) # 按行求均值var = ((X - mean) ** 2).mean(dim=0) # 按行求方差else: # 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。mean = X.mean(dim=(0, 2, 3), keepdim=True) # 保持X的形状(即第1维,输出通道数)以便后面可以做广播运算,结果的形状是1*n*1*1var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)X_hat = (X - mean) / torch.sqrt(var + eps) # 训练模式下,用当前的均值和方差做标准化# 更新移动平均的均值和方差moving_mean = momentum * moving_mean + (1.0 - momentum) * meanmoving_var = momentum * moving_var + (1.0 - momentum) * varY = gamma * X_hat + beta # 缩放和移位return Y, moving_mean.data, moving_var.data
class BatchNorm(nn.Module):# num_features:完全连接层的输出数量或卷积层的输出通道数。# num_dims:2表示完全连接层,4表示卷积层def __init__(self, num_features, num_dims):super().__init__()if num_dims == 2:shape = (1, num_features)else:shape = (1, num_features, 1, 1)# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成1和0self.gamma = nn.Parameter(torch.ones(shape))self.beta = nn.Parameter(torch.zeros(shape))# 非模型参数的变量初始化为0和1self.moving_mean = torch.zeros(shape)self.moving_var = torch.ones(shape)def forward(self, X):# 如果X不在内存上,将moving_mean和moving_var# 复制到X所在显存上if self.moving_mean.device != X.device:self.moving_mean = self.moving_mean.to(X.device)self.moving_var = self.moving_var.to(X.device)# 保存更新过的moving_mean和moving_varY, self.moving_mean, self.moving_var = batch_norm(X, self.gamma, self.beta, self.moving_mean,self.moving_var, eps=1e-5, momentum=0.9)return Y
7.5.4 使用批量规范化层的 LeNet
net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),nn.Linear(84, 10))
学习率拉的好大。
lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
loss 0.262, train acc 0.902, test acc 0.879
20495.7 examples/sec on cuda:0

7.5.5 简明实现
net1 = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),nn.Linear(84, 10))
d2l.train_ch6(net1, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
loss 0.263, train acc 0.903, test acc 0.870
36208.4 examples/sec on cuda:0

7.5.6 争议
这个东西就是玄学,有效但是不知大为什么有效。作者给出的解释是“减少内部协变量偏移”,但是也是处于直觉而不是证明。
练习
(1)在使用批量规范化之前,我们是否可以从全连接层或者卷积层中删除偏置函数?为什么?
我认为可以,偏置会在减去均值时消去,此外,BN 中也是带偏移参数的。
(2)比较 LeNet 在使用和不使用批量规范化情况下的学习率。
a. 绘制训练和测试精准度的提高。b. 学习率有多高?
学习率相同的话,使用批量规范化的收敛速度会非常快。
(3)我们是否需要在每个层中进行批量规范化?尝试一下?
net2 = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),nn.Linear(256, 120), nn.Sigmoid(),nn.Linear(120, 84), nn.Sigmoid(),nn.Linear(84, 10))lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net2, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
loss 0.349, train acc 0.871, test acc 0.856
37741.0 examples/sec on cuda:0

去掉后面两个之后曲线稳多了。
(4)可以通过批量规范化来替换暂退法吗?行为会如何改变?
看来还是批量规范化好些
net3 = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),nn.Linear(256, 120), nn.Sigmoid(),nn.Dropout(p=0.1),nn.Linear(120, 84), nn.Sigmoid(),nn.Dropout(p=0.1),nn.Linear(84, 10))lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net3, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
loss 0.541, train acc 0.790, test acc 0.748
40642.6 examples/sec on cuda:0

(5) 确定参数 gamma 和 beta,并观察和分析结果。
net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))
(tensor([3.1800, 1.6709, 4.0375, 3.4801, 2.6182, 2.3103], device='cuda:0',grad_fn=<ReshapeAliasBackward0>),tensor([ 3.5415, 1.6295, 1.8926, -1.5510, -2.4556, 1.1020], device='cuda:0',grad_fn=<ReshapeAliasBackward0>))
(6)查看高级 API 中关于 BatchNorm 的在线文档,以了解其他批量规范化的应用。
略。
(7)研究思路:可以应用的其他“规范化”变换有哪些,可以应用概率积分变换吗,全秩协方差估计呢?
略。
相关文章:

《动手学深度学习 Pytorch版》 7.5 批量规范化
7.5.1 训练深层网络 训练神经网络的实际问题: 数据预处理的方式会对最终结果产生巨大影响。 训练时,多层感知机的中间层变量可能具有更广的变化范围。 更深层的网络很复杂容易过拟合。 批量规范化对小批量的大小有要求,只有批量大小足够…...

Toaster - Android 吐司框架,专治 Toast 各种疑难杂症
官网 https://github.com/getActivity/Toaster 这可能是性能优、使用简单,支持自定义,不需要通知栏权限的吐司 想了解实现原理的可以点击此链接查看:Toaster 源码 集成步骤 如果你的项目 Gradle 配置是在 7.0 以下,需要在 bui…...

2023年9月26日,历史上的今天大事件早读
1620年9月26日大明皇帝朱常洛驾崩 1815年9月26日俄、普、奥三国在巴黎发表缔结“神圣同盟” 1841年9月26日清代思想家、诗人龚自珍逝世 1849年9月26日“生理学之父”巴甫洛夫诞生 1909年9月26日云南陆军讲武堂创办 1953年9月26日画家徐悲鸿逝世 1980年9月26日国际宇航联合…...

CListCtrl控件为只显示一列,持滚动显示其他,不用SetScrollFlags
CListCtrl控件为只显示一列,持滚动显示其他,不用SetScrollFlags 2023/9/5 下午4:52:58 如果您不希望使用 SetScrollFlags 函数来设置滚动条样式,可以使用以下代码将 CListCtrl 控件设置为只显示一列,并支持滚动显示其他内容: cpp // 设置控件样式和属性 m_listCtrl.Se…...

spring博客实现分页查询
1、首先创建dto下的分页类PageBean package com.zzz.blog.dto;import java.util.List;public class PageBean {private Integer pageSize; //页面大小private Integer currentPage; //当前页private Integer totalCount; //总条数private Integer totalPage; //总页数private …...
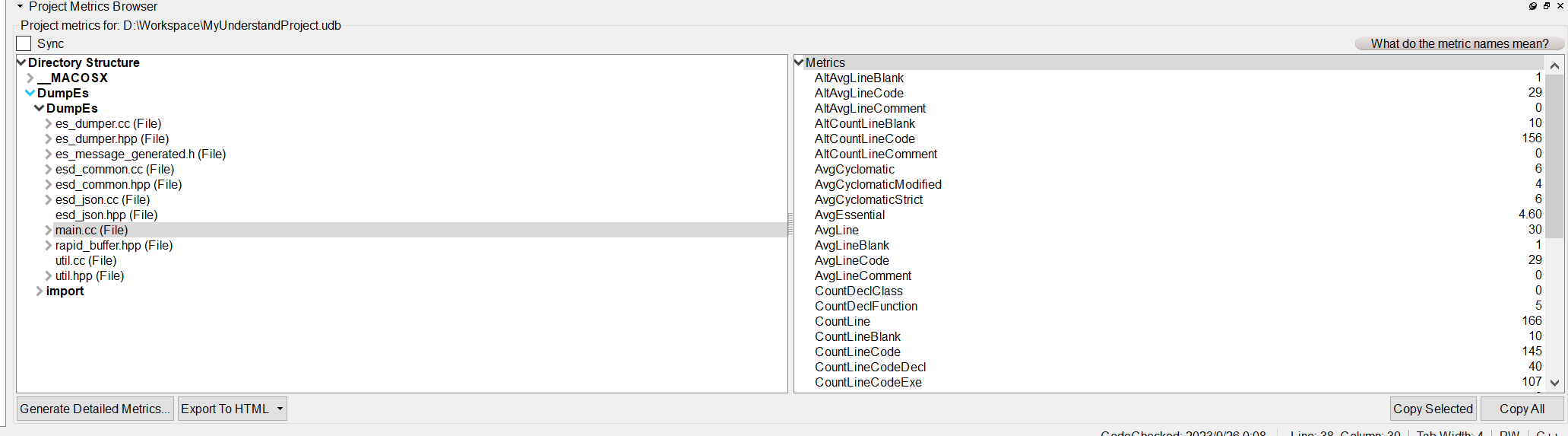
代码阅读分析神器-Scitools Understand
这里写目录标题 前言概要功能介绍1.代码统计2.图形化分析3.代码检查 使用方法下载及使用 前言 作为一名程序员,阅读代码是一个必须要拥有的能力,但无奈很多代码逻辑嵌套非常多,看起来非常吃力,看了那段逻辑就忘记了刚才的逻辑&am…...

学霸吐血整理‼《2023 年 IC 验证岗面试真题解析》宝藏干货!
Q1.定宽数组、动态数组、关联数组、队列各自的特点和使用方式。 Q2.fork…join/fork…join_any/fork…join_none 之间的异同 Q3.mailbox、event、semaphore 之间的异同 Q4.(event_handle)和 wait(event_handle.triggered)区别 Q5.task 和 function 异同区别 Q6.使用 clocking b…...

稳定性、可靠性、可用性、灵活性、解耦性
稳定性 平衡的能力 Linux系统的OOM机制、tcp的拥塞控制 可靠性 确定的能力 tcp的ACK、HA机制、加密 可用性 复原的能力 负债均衡、tcp的重传、冗余机制、故障域 灵活性 界限的能力 用户态、restful api、IP地址掩码 解耦性 不依赖的能力 分布式、SDN、容器、操作…...

docker搭建Redis三主三从
docker搭建Redis三主三从 首先启动6个redis进入容器构建主从关系连接进入6381作为切入点,查看集群状态 首先启动6个redis [rootdocker redis-node-1]# cat /etc/hosts 127.0.0.1 localhost localhost.localdomain localhost4 localhost4.localdomain4 ::1 …...

亚马逊要求的UL报告的产品标准是什么?如何区分
亚马逊为什么要求电子产品有UL检测报告? 首先,美国是一个对安全要求非常严格的国家,美国本土的所有电子产品生产企业早在很多年前就要求有相关安规检测。 其次,随着亚马逊在全球商业的战略地位不断提高,境外的电子设…...
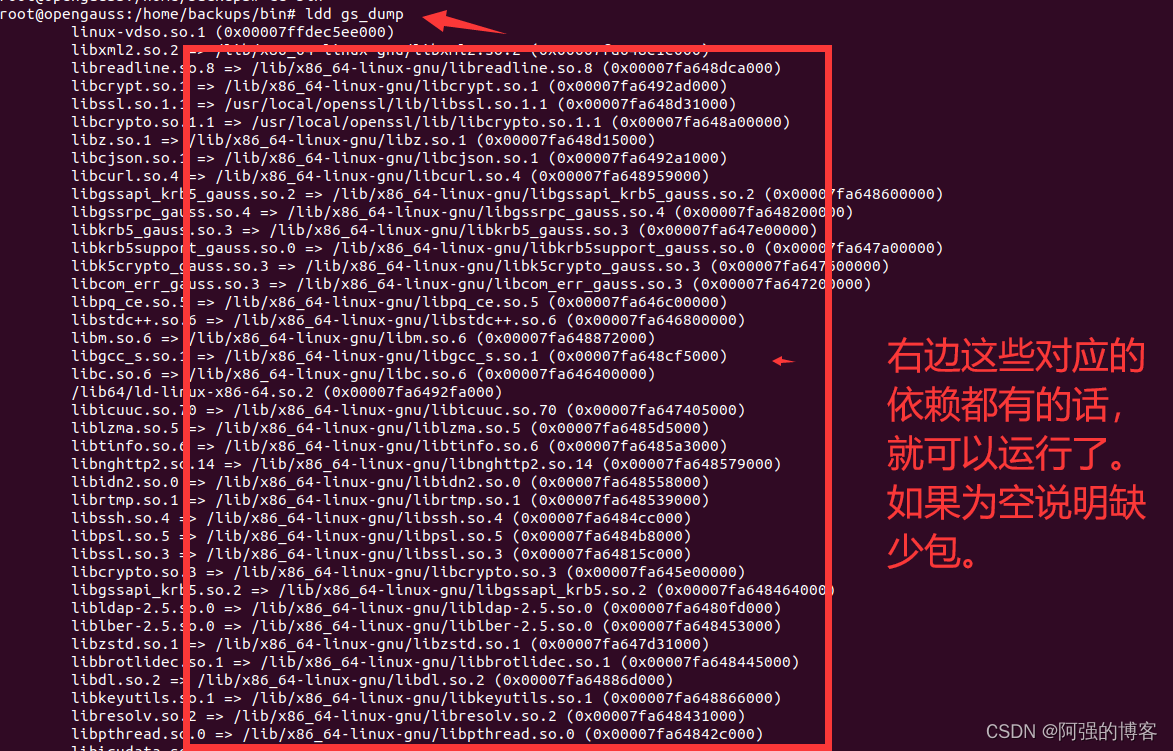
如何在linux定时备份opengauss数据库(linux核心至少在GLIBC_2.34及以上)
前提环境,linux的核心至少在GLIBC_2.34及以上才能使用。 查看linux的glibc版本的命令如下 strings /lib64/libc.so.6 | grep GLIBC 如下图 或者用ldd --version 如下图 在官网下载对应的依赖包, 只需要这个lib文件即可,将这个包放在lin…...
——Skywalking UI 界面简介)
SkyWalking快速上手(七)——Skywalking UI 界面简介
文章目录 前言1. 仪表盘1.1 指标展示1.2 自定义仪表盘 2. 拓扑图2.1 节点展示2.2 连接展示 3. 追踪3.1 请求链路3.2 请求详情 4. 性能剖析4.1 方法级别性能分析4.2 代码级别性能分析 5. 告警5.1 告警规则设置5.2 告警通知 6. 日志记录6.1 日志展示6.2日志分析6.3代码示例 总结 …...
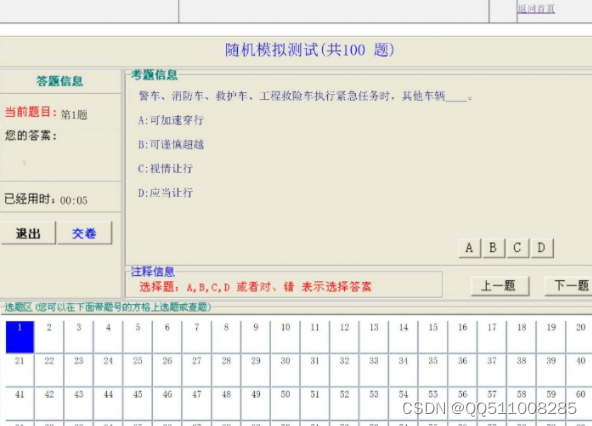
python+vue驾校驾驶理论考试模拟系统
管理员的主要功能有: 1.管理员输入账户登陆后台 2.个人中心:管理员修改密码和账户信息 3.用户管理:管理员可以对用户信息进行添加,修改,删除,查询 4.添加选择题:管理员可以添加选择题目…...

go-redis 框架基本使用
文章目录 redis使用场景下载框架和连接redis1. 安装go-redis2. 连接redis 字符串操作有序集合操作流水线事务1. 普通事务2. Watch redis使用场景 缓存系统,减轻主数据库(MySQL)的压力。计数场景,比如微博、抖音中的关注数和粉丝数…...
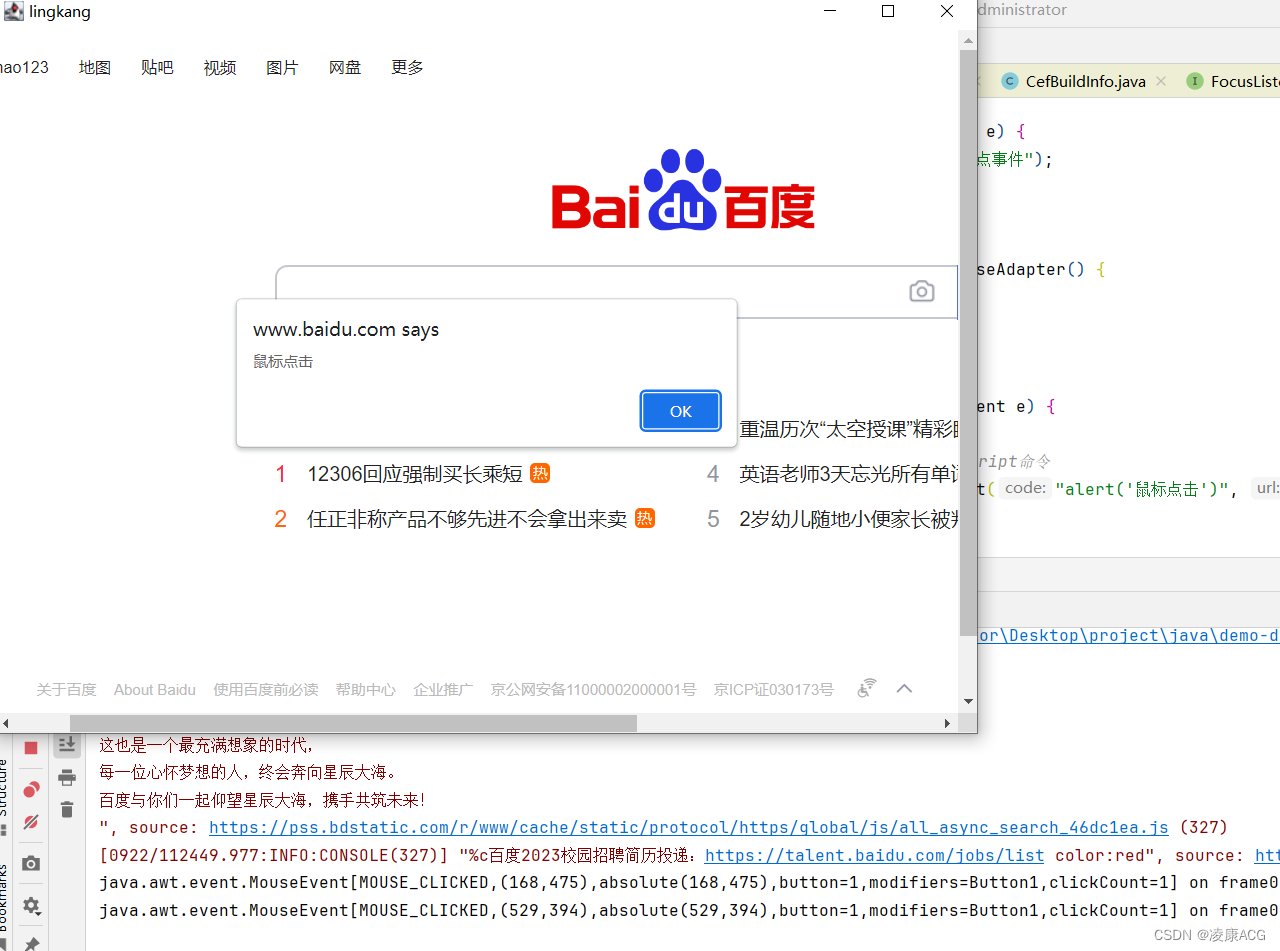
java内嵌浏览器CEF-JAVA、jcef、java chrome
java内嵌浏览器CEF-JAVA、jcef、java chrome jcef是老牌cef的chrome内嵌方案,可以进行java-chrome-h5-桌面开发,下面为最新版本(2023年9月22日10:33:07) JCEF(Java Chromium Embedded Framework)是一个基于…...

string类模拟实现——C++
一、构造与析构 1.构造函数 构造函数需要尽可能将成员在初始化列表中初始化,string类的成员这里自定义的和顺序表相似,有_str , _size , _capacity , 以及一个静态成员 npos ,构造函数这里实现两种,一种是传参为常量字符串的&am…...
来拼接字符串。但是,如果需要拼接多个字符串或表中的字段,就需要使用内置的拼接函数了)
在 SQL Server 中,可以使用加号运算符(+)来拼接字符串。但是,如果需要拼接多个字符串或表中的字段,就需要使用内置的拼接函数了
以下是 SQL Server 中的一些内置拼接函数: 1. CONCAT:将两个或多个字符串拼接在一起。语法为: CONCAT (string1, string2, ...)示例: SELECT CONCAT(Hello, , World) as combined_string;输出结果为:Hello World&a…...
蓝桥杯每日一题2023.9.25
4406. 积木画 - AcWing题库 题目描述 分析 在完成此问题前可以先引入一个新的问题 291. 蒙德里安的梦想 - AcWing题库 我们发现16的二进制是 10000 15的二进制是1111 故刚好我们可以从0枚举到1 << n(相当于二的n次方的二进制表示) 注:奇数个0…...
)
前端面试的话术集锦第 20 篇博文——高频考点(输入 URL 到页面渲染的整个流程)
这是记录前端面试的话术集锦第二十篇博文——高频考点(输入 URL 到页面渲染的整个流程),我会不断更新该博文。❗❗❗ 借用这道经典面试题,将之前学习到的浏览器以及网络几章节的知识联系起来。 首先是DNS查询,如果这一步做了智能DNS解析的话,会提供访问速度最快的IP地址…...
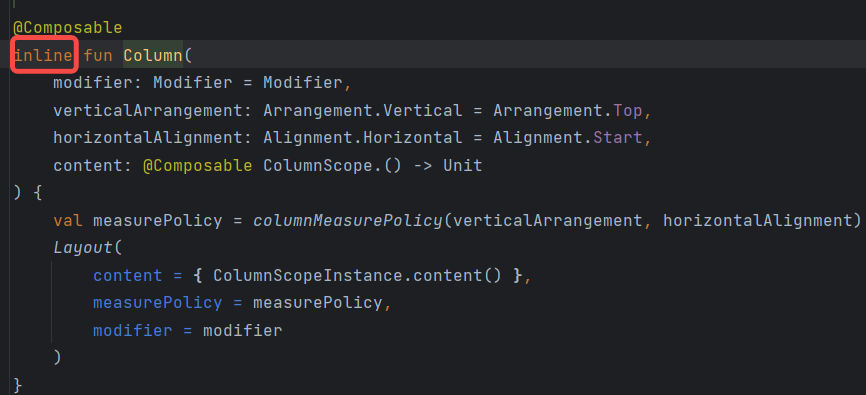
Android Jetpack Compose之确定重组范围并优化重组
目录 1.概述2.确定Composable重组的范围3.优化重组的性能3.1 Composable 位置索引3.2 通过Key添加索引信息3.3 使用注解Stable优化重组 1.概述 前面的文章提到Compose的重组是智能的,Composable函数在进行重组时会尽可能的跳过不必要的重组,只对需要变化…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
