前端碎知识点
1 统计字符串中每个字符出现的频率
const str = 'fgasdfadfdasd';const result = str.split('').reduce((a, b) => {if (a[b]) {a[b]++;} else {a[b] = 1;}return a;
}, {});const resultNew = str.split('').reduce((a, b) => {// undefined++,就是NaNa[b]++ || (a[b] = 1);return a;
}, {});const resultNew2 = str.split('').reduce((a, b) =>(a[b]++ || (a[b] = 1), a), {});// { f: 3, g: 1, a: 3, s: 2, d: 4 }
2 类型转化
const res = ++[[]][+[]] + [+[]];
// 使用优先级最低的进行分割,优先级最低的是 + 1. 分解
++[[]][+[]]
+
[+[]] 2. 分解 ++
++ [[]][+[]]
+
[+[]] 3. 计算 [[]][+[]]
[[]],创建了数组,数组只有一个元素[]
+[],首先调用[].valueOf(),得到的结果还是[];
+[],接着调用[].toString(),得到的结果是'';
+[],最终结果为 0;
表达式相当于 [[]][0],即[]4. 计算 ++[]
结果为1;5. 计算 [+[]]
+[]为0, [+[]]为[0]6. 最终结果
最终结果变为 1 + [0]
[0]转化为'0',最终结果是'10';
3 复合属性
backgroud属于复合属性,包括url背景,尺寸等等;
如果在关闭背景closed样式中直接更改backgroud,那么之前的backgroud样式将被全部覆盖;
正确的做法:只更改backgroud-img样式,其他样式正常使用;
正常背景
<div class="head-music"></div>
.head-music {backgroud: url(../asset/music.png)width: 30px;height: 30px;
}关闭背景
<div class="head-music closed"></div>
.head-music.closed {backgroud: url(../asset/closed.png);
}正确关闭背景
<div class="head-music closed"></div>
.head-music.closed {backgroud-image: url(../asset/closed.png);
}
4 算法
给定一个仅包含数字2-9的字符串,返回所有它能表示的字母组合;答案可以按任意顺序返回。
给出数字到字母的映射如下:
2:abc
3:def
4:ghi
5:jkl
6:mno
7:pqrs
8:tuv
9:wxyz
function _compose(arr1, arr2) {let r = []; // 组合结果if (arr1.length === 0) return arr2;if (arr2.length === 0) return arr1;for (let i = 0; i < arr1.length; i++) {for (let j = 0; j < arr2.length; j++) {r.push(arr1[i] + arr2[j]);}}return r;
};const keyboardMap = (digits) => {let result = [];const map = [, , 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz'];for (let i = 0; i < digits.length; i++) {result = _compose(result, map[digits[i]]);}return result;
}const res = keyboardMap('2345');
console.log('===>res', res);5 Promise
Promise调用then方法,会产生新的promise
Promise.resolve().then(() => {console.log(0);return Promise.resolve(4);}).then((res) => {console.log('res', res);});Promise.resolve().then(() => {console.log(1);}).then((res) => {console.log('===>res', res);console.log(2);}).then(() => {console.log(3);}).then(() => {console.log(5);}).then(() => {console.log(6);});// 0
// 1
// ===> res undefined
// 2
// 3
// res 4
// 5
// 6相关文章:

前端碎知识点
1 统计字符串中每个字符出现的频率 const str fgasdfadfdasd;const result str.split().reduce((a, b) > {if (a[b]) {a[b];} else {a[b] 1;}return a; }, {});const resultNew str.split().reduce((a, b) > {// undefined,就是NaNa[b] || (a[b] 1);ret…...

【Leetcode Sheet】Weekly Practice 7
Leetcode Test 1462 课程表Ⅳ(9.12) 你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] [ai, bi] 表示如果你想选 bi 课程,你 必须 先选 ai 课程。 有的课会有直接…...
回文链表)
leetcode Top100(23)回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 输入:head [1,2,2,1] 输出:true采用动态数组,判断数组对称就可以了(这解法空间…...
WebGL绘制圆形的点
目录 前言 如何实现圆形的点? 片元着色器内置变量(gl_FragCoord、gl_PointCoord) gl_PointCoord的含义 示例程序(RoundedPoint.js) 代码详解 前言 本文将讨论示例程序RoundedPoint,该程序绘制了圆…...

《The Rise and Potential of Large Language Model Based Agents: A Survey》全文翻译
The Rise and Potential of Large Language Model Based Agents: A Surve - 基于 LLMs 的代理的兴起和潜力:一项调查 论文信息摘要1. 介绍2. 背景2.1 AI 代理的起源2.2 代理研究的技术趋势2.3 为什么大语言模型适合作为代理大脑的主要组件 论文信息 题目࿱…...
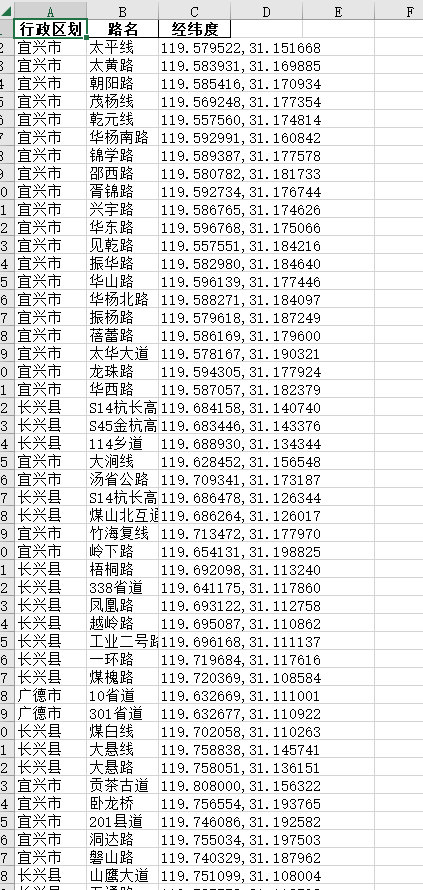
在线地图获取城市路网数据
在线地图获取城市路网数据 近期科研项目中,需要获取城市路网数据,于是详细阅读各大在线地图api接口,总结出来这么一条可行的思路: 首先获取城市轮廓根据城市轮廓把城市分割成若干个小块在每个小块中根据在线地图的POI检索接口&a…...
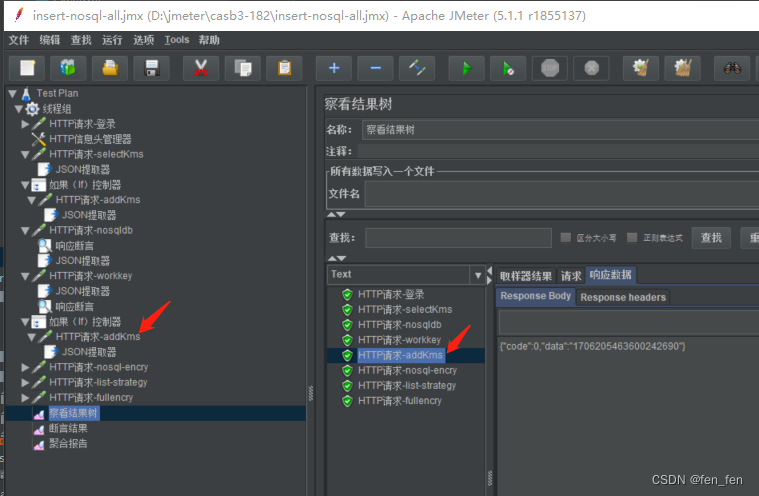
8.2 Jmeter if控制器使用
前提:jmeter脚本需要用到if控制器,if判断如果查询不到,则去新增。 1、添加if控制器 线程组-->逻辑控制器-->如果(if)控制器 1)、Expression (must evaluate to true or false) :表达式(值必须是tru…...

科技云报道:青云科技打出“AI算力牌”,抢跑“云+AI”新增市场
科技云报道原创。 近三年,中国云计算市场在多个维度同时发生着剧烈变化——疫情极大加速了全社会对于数字化的认知和接受程度;一系列云原生技术依托着开源和蓬勃的市场而迅速发展演变,更多产品和技术名词同时涌向市场;国际关系复…...
学习路之PHP--lumen安装配置
一、下载lumen源码 composer create-project --prefer-dist laravel/lumen blog 安装lumen-generator composer require flipbox/lumen-generator 二、配置 bootstrap\app.php 97行 $app->register(Flipbox\LumenGenerator\LumenGeneratorServiceProvider::class);三、生成…...
【C++】构造函数和析构函数第一部分(构造函数和析构函数的作用)--- 2023.9.25
目录 前言初始化和清理的概念构造函数和析构函数的作用构造函数的作用析构函数的作用 使用构造函数和析构函数的注意事项默认的构造函数和析构函数结束语 前言 在使用c语言开发的项目场景中,我们往往会遇到申请空间的需求,同时也肯定遇到过程序运行一段…...
CocosCreator Tween系统理解)
CocosCreator3.8研究笔记(二十一)CocosCreator Tween系统理解
在 Cocos Creator 3.x 版本中, Tween系统代替了原来的Action系统。很多朋友不明白Tween到底是什么,Tween原理是什么?怎么使用Tween? 今天就来详细了解一下,希望能帮助到大家加深对Tween的了解,并快速掌握Tw…...

大数据学习-目录
学习内容持续更新ing 1.大数据学习1.0-Centos8虚拟机安装 大数据学习1.0-Centos8虚拟机安装_汉卿HanQ的博客-CSDN博客 2.大数据学习1.1-Centos8网络配置 大数据学习1.1-Centos8网络配置_汉卿HanQ的博客-CSDN博客 3.大数据学习1.2-yum配置 大数据学习1.2-yum配置_汉卿HanQ的…...

《动手学深度学习 Pytorch版》 7.5 批量规范化
7.5.1 训练深层网络 训练神经网络的实际问题: 数据预处理的方式会对最终结果产生巨大影响。 训练时,多层感知机的中间层变量可能具有更广的变化范围。 更深层的网络很复杂容易过拟合。 批量规范化对小批量的大小有要求,只有批量大小足够…...

Toaster - Android 吐司框架,专治 Toast 各种疑难杂症
官网 https://github.com/getActivity/Toaster 这可能是性能优、使用简单,支持自定义,不需要通知栏权限的吐司 想了解实现原理的可以点击此链接查看:Toaster 源码 集成步骤 如果你的项目 Gradle 配置是在 7.0 以下,需要在 bui…...

2023年9月26日,历史上的今天大事件早读
1620年9月26日大明皇帝朱常洛驾崩 1815年9月26日俄、普、奥三国在巴黎发表缔结“神圣同盟” 1841年9月26日清代思想家、诗人龚自珍逝世 1849年9月26日“生理学之父”巴甫洛夫诞生 1909年9月26日云南陆军讲武堂创办 1953年9月26日画家徐悲鸿逝世 1980年9月26日国际宇航联合…...

CListCtrl控件为只显示一列,持滚动显示其他,不用SetScrollFlags
CListCtrl控件为只显示一列,持滚动显示其他,不用SetScrollFlags 2023/9/5 下午4:52:58 如果您不希望使用 SetScrollFlags 函数来设置滚动条样式,可以使用以下代码将 CListCtrl 控件设置为只显示一列,并支持滚动显示其他内容: cpp // 设置控件样式和属性 m_listCtrl.Se…...

spring博客实现分页查询
1、首先创建dto下的分页类PageBean package com.zzz.blog.dto;import java.util.List;public class PageBean {private Integer pageSize; //页面大小private Integer currentPage; //当前页private Integer totalCount; //总条数private Integer totalPage; //总页数private …...
代码阅读分析神器-Scitools Understand
这里写目录标题 前言概要功能介绍1.代码统计2.图形化分析3.代码检查 使用方法下载及使用 前言 作为一名程序员,阅读代码是一个必须要拥有的能力,但无奈很多代码逻辑嵌套非常多,看起来非常吃力,看了那段逻辑就忘记了刚才的逻辑&am…...

学霸吐血整理‼《2023 年 IC 验证岗面试真题解析》宝藏干货!
Q1.定宽数组、动态数组、关联数组、队列各自的特点和使用方式。 Q2.fork…join/fork…join_any/fork…join_none 之间的异同 Q3.mailbox、event、semaphore 之间的异同 Q4.(event_handle)和 wait(event_handle.triggered)区别 Q5.task 和 function 异同区别 Q6.使用 clocking b…...

稳定性、可靠性、可用性、灵活性、解耦性
稳定性 平衡的能力 Linux系统的OOM机制、tcp的拥塞控制 可靠性 确定的能力 tcp的ACK、HA机制、加密 可用性 复原的能力 负债均衡、tcp的重传、冗余机制、故障域 灵活性 界限的能力 用户态、restful api、IP地址掩码 解耦性 不依赖的能力 分布式、SDN、容器、操作…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
