EM@基本初等函数@幂和根式@指数函数
abstract
- 基本初等函数@幂和根式@指数函数
指数和幂
正整指数幂
-
a n a^{n} an= a ⋯ a ⏟ n 个 \underbrace{a\cdots{a}}_{n个} n个 a⋯a, n ∈ N + n\in\mathbb{N^{+}} n∈N+
-
其中 a n a^{n} an称为** a a a的 n n n次幂**
-
a a a叫做幂的底数, n n n叫做幂的指数
-
正整指数幂满足: a m a n = a m − n \frac{a^{m}}{a^{n}}=a^{m-n} anam=am−n, ( m > n , a ≠ 0 ) (m>n,a\neq{0}) (m>n,a=0)
-
也可以递归地定义成:
a n = { 1 ( n = 0 ) a ⋅ a n − 1 ( n > 0 ) ( 1 a ) − n ( n < 0 ) {\displaystyle a^{n}={\begin{cases}1&(n=0)\\ a\cdot a^{n-1}&(n>0)\\ \left({\frac {1}{a}}\right)^{-n}&(n<0)\end{cases}}} an=⎩ ⎨ ⎧1a⋅an−1(a1)−n(n=0)(n>0)(n<0)
整数指数幂
-
将 a m a n = a m − n , ( m > n , a ≠ 0 ) \frac{a^{m}}{a^{n}}=a^{m-n},(m>n,a\neq{0}) anam=am−n,(m>n,a=0)的条件 m > n m>n m>n取消,则推广到了整数指数幂( m − n ∈ Z m-n\in{\mathbb{Z}} m−n∈Z)
- 例如 a 3 a 5 \frac{a^{3}}{a^{5}} a5a3= a − 2 a^{-2} a−2
-
整数指数幂中规定 a 0 = 1 , ( a ≠ 0 ) a^{0}=1,(a\neq{0}) a0=1,(a=0), a − n = 1 a n a^{-n}=\frac{1}{a^{n}} a−n=an1, a ≠ 0 a\neq{0} a=0, n ∈ N + n\in{\mathbb{N^{+}}} n∈N+
-
即任何负整数次幂的计算都可以转化为含正整数指数幂的算式表示和计算
-
例如 a − 2 a^{-2} a−2= a 0 a 2 \frac{a^{0}}{a^{2}} a2a0= 1 a 2 \frac{1}{a^{2}} a21
-
Note: a = 0 a=0 a=0时 a 0 a^{0} a0比较特殊,参考幂 (wikipedia.org)
- 如果要给它( 0 0 0^0 00)指定一个值,通常是1
- 若 a = 0 a=0 a=0, a − 2 = a 0 a 2 a^{-2}=\frac{a^{0}}{a^{2}} a−2=a2a0没有意义,但在其他地方,使用有定义的 0 0 0^{0} 00是方便的
- 在中学阶段可姑且认为 0 0 0^{0} 00没有定义
方根和分数指数幂
- 下面讨论实数范围内的方根概念
- 和根的个数相关的结论都限定在实数范围内
- 复数范围内在此不讨论
简单低次方根
- x 2 = a x^2=a x2=a,则 x x x称为 a a a的平方根或二次方根
- 实数范围i内的平方根情况分析:
- 若 a > 0 a>0 a>0,则 x = ± a x=\pm{\sqrt{a}} x=±a,共2个平方根
- 若 a = 0 a=0 a=0,则 x = 0 x=0 x=0,仅一个平方根
- 若 a < 0 a<0 a<0,则实数范围内没有平方根
- 实数范围i内的平方根情况分析:
- x 3 = a x^3=a x3=a,则 x x x称为 a a a的立方根或三次方根
- 实数范围内, x 3 = a x^3=a x3=a有且仅有1个根 a 3 \sqrt[3]{a} 3a
- Note:根据代数学基本定理,复数范围内有3个立方根(包含重根)
n n n次方根
-
若 ∃ x \exist{x} ∃x s.t. x n = a x^{n}=a xn=a, ( a ∈ R , n > 1 , n ∈ N + ) (a\in{\mathbb{R}},n>1,n\in{\mathbb{N}_{+}}) (a∈R,n>1,n∈N+),则 x x x是实数** a a a的 n n n次方根**
-
Note: n n n次方根是 n n n为正整数的范围内讨论的
-
求 a a a的 n n n次方根,称为"把 a a a开 n n n次方",称为开方运算
-
为了把 a a a的 n n n次方根 x x x表示为形如 x = f ( a ) x=f(a) x=f(a)的形式,引入记号 a n \sqrt[n]{a} na,
- 当 a > 0 a>0 a>0且 n n n为偶数时, a n \sqrt[n]{a} na表示的是 a a a的两个 n n n次方根中的正根
- 所以正数的偶次方根(共2个)使用该符号的算式表示为 a n \sqrt[n]{a} na, − a n -\sqrt[n]{a} −na
- 当 a < 0 a<0 a<0时,其只有奇次方根,表示为 a n \sqrt[n]{a} na
- n n n为奇数时, a a a的 n n n次方根只有一个,也记为 a n \sqrt[n]{a} na
- 当 a > 0 a>0 a>0且 n n n为偶数时, a n \sqrt[n]{a} na表示的是 a a a的两个 n n n次方根中的正根
-
总之 a n \sqrt[n]{a} na表示的是 a a a的唯一奇数次方根或者两个互为相反数的偶次方根中的正根(非负根),具体要视 a , n a,n a,n的取值而定
- 例如 a n n \sqrt[n]{a^n} nan,若 n n n是偶数,则 a n ⩾ 0 a^{n}\geqslant{0} an⩾0, b = a n n b=\sqrt[n]{a^n} b=nan是 a n a^{n} an的 n n n次方根中的非负根
- b n = a n b^{n}=a^{n} bn=an,任意 ∣ b ∣ = ∣ a ∣ |b|=|a| ∣b∣=∣a∣都满足该等式
- 因为 b ⩾ 0 b\geqslant{0} b⩾0,所以 b = ∣ a ∣ b=|a| b=∣a∣,即 a n n = ∣ a ∣ \sqrt[n]{a^n}=|a| nan=∣a∣( n n n为偶数)
- 例如: ( − 3 ) 2 2 = ∣ − 3 ∣ = 3 \sqrt[2]{(-3)^2}=|-3|=3 2(−3)2=∣−3∣=3
- 同样是 b = a n n b=\sqrt[n]{a^n} b=nan,若 n n n为奇数, a , a n , b a,a^{n},b a,an,b同号,由 n n n次方根的定义,仍有 b n = a n b^{n}=a^{n} bn=an,从而 b = a b=a b=a( n n n为奇数)
- 例如 a n n \sqrt[n]{a^n} nan,若 n n n是偶数,则 a n ⩾ 0 a^{n}\geqslant{0} an⩾0, b = a n n b=\sqrt[n]{a^n} b=nan是 a n a^{n} an的 n n n次方根中的非负根
n次方根的表示
任意数可以开奇次方,但不是任意数都可以开偶次方
- 偶次方根:正数可以开偶次方根
- 正数 a a a的偶次方根有2个互为相反数的根,它们分别表示为 a n \sqrt[n]{a} na, − a n -\sqrt[n]{a} −na,( a a a为偶数)
- 负数 a a a的偶次方根没有意义(没有实根,但是在复数范围内有意义)
- 奇次方根:任何实数可以开奇次方根
- ∀ a ∈ R \forall a\in\mathbb{R} ∀a∈R与其唯一的奇次方根 a n \sqrt[n]{a} na同号,即 a a n ⩾ 0 a\sqrt[n]a\geqslant{0} ana⩾0,( n n n为奇数)
根式@根指数
- 当 a n \sqrt[n]{a} na有意义时, a n \sqrt[n]{a} naj叫做根式,其中 n n n为根式的指数,称为根指数
- 例如, 2 \sqrt{2} 2, 5 3 \sqrt[3]{5} 35, − 2 3 \sqrt[3]{-2} 3−2,它们都有意义,都是根式
算术根
- 正数 a a a的正 n n n次方根(大于0的那个 n n n次方根)叫做** a a a的 n n n次算术根**
- 任意正数的奇次方根都是正数和偶次方根也恰好有一个正数,所以任意正数 a a a总是存在任意次算术根
- 任意负数的奇次方根是负数,偶次方根无意义,所以负数不存在任意次算术根
- 例如 a = 5 a=5 a=5的 2 2 2次算术根为 5 \sqrt{5} 5,而平方根有 − 5 , 5 -\sqrt{5},\sqrt{5} −5,5两个, a = 5 a=5 a=5的 3 3 3次算术根为 5 3 \sqrt[3]{5} 35,立方根也是仅有 5 3 \sqrt[3]{5} 35
- a = 0 , a = − 2 a=0,a=-2 a=0,a=−2是都不是正数,因此它们不存在任何次算术平方根
几个"总是"
- 任意数的奇次方根总是有意义的
- 正数的任意次方根总是存在(偶次方根和奇次方根都存在)
根式性质
- 根据 n n n次方根的定义,有
- ( a n ) n = a (\sqrt[n]{a})^{n}=a (na)n=a, ( n > 1 , n ∈ N + ) (n>1,n\in{\mathbb{N}_{+}}) (n>1,n∈N+)
- a n n \sqrt[n]{a^{n}} nan= { a n 为奇数 ∣ a ∣ n 为偶数 \begin{cases}a&n为奇数\\|a|&n为偶数\end{cases} {a∣a∣n为奇数n为偶数
分数指数幂
既约分数
- 本节讨论的分数是既约分数,即最简分数,
- 例如 4 3 \frac{4}{3} 34是既约分数,而 8 6 \frac{8}{6} 68不是既约的
正分数指数幂
- 我们借助 n n n次方根来规定和定义正分数指数幂
- 若约定 a 1 n = a n a^{\frac{1}{n}}=\sqrt[n]{a} an1=na, ( a > 0 , n ∈ N + ) (a>0,n\in\mathbb{N_{+}}) (a>0,n∈N+)
- a m n a^{\frac{m}{n}} anm= ( a n ) m (\sqrt[n]{a})^{m} (na)m= a m n \sqrt[n]{a^{m}} nam, ( a > 0 , n , m ∈ N + , m n 是既约分数 ) (a>0,n,m\in{\mathbb{N_{+}}},\frac{m}{n}是既约分数) (a>0,n,m∈N+,nm是既约分数)
负分数指数幂
- 和负整数指数幂的意义相同,同样可以规定
- a − m n a^{-\frac{m}{n}} a−nm= 1 a m n \frac{1}{a^{\frac{m}{n}}} anm1, ( a > 0 , m , n ∈ N + ) (a>0,m,n\in\mathbb{N_{+}}) (a>0,m,n∈N+), m n 是既约分数 \frac{m}{n}是既约分数 nm是既约分数
判定一个分数指数幂是否有意义
- a = ( − 2 ) 4 3 a=(-2)^{\frac{4}{3}} a=(−2)34= ( − 2 ) 4 3 \sqrt[3]{(-2)^{4}} 3(−2)4,而 b = ( − 2 ) 8 6 b=(-2)^{\frac{8}{6}} b=(−2)68= ( − 2 ) 8 6 \sqrt[6]{(-2)^{8}} 6(−2)8,显然 a = b a=b a=b
- 第一个式子 a a a我们只需要看到分数指数 4 3 \frac{4}{3} 34中分母为奇数 3 3 3,就可以断言 a a a一定有意义
- 第二个式子 b b b,其分数指数 8 6 \frac{8}{6} 68的分子式偶数,那么也可以确定 b b b必定有意义
- 总之, a < 0 a<0 a<0;分子 m m m,为奇数,分母 n n n为偶数,则 a m n a^{\frac{m}{n}} anm无意义
- 其中分母 n n n和偶次方根挂钩,负数的偶次方根无意义
- 分子 m m m若为偶数,那么 a n a^{n} an非负,其任意次方根均有意义
- a a a本身若非负,那么 a n a^{n} an非负,则 a m n a^{\frac{m}{n}} anm相当于非负数的方根,其任意次方根均有意义
小结@有理指数幂
-
上述讨论中,我们从正整数指数幂一路推广到分数指数幂(有理指数幂)
-
设 a , b > 0 a,b>0 a,b>0, ∀ α , β ∈ Q \forall{\alpha,\beta}\in\mathbb{Q} ∀α,β∈Q,有理数指数幂有运算法则:
- a α α β a^{\alpha}\alpha^{\beta} aααβ= a α + β a^{\alpha+\beta} aα+β
- ( a α ) β (a^{\alpha})^{\beta} (aα)β= a α β a^{\alpha\beta} aαβ
- ( a b ) α = a α b α (ab)^{\alpha}=a^{\alpha}b^{\alpha} (ab)α=aαbα
-
其中性质2是幂的幂的性质,性质3体现了指数运算对乘运算的分配律
无理数指数幂和实数指数幂
- 无理数指数幂 a n a^{n} an, n ∈ R − Q n\in\mathbb{R-Q} n∈R−Q,其中 R − Q \mathbb{R-Q} R−Q表似乎无理数集合
- 设 n 1 , n 2 n_1,n_2 n1,n2分别是 n n n的有理不足近似和过剩近似,并将 n n n的任意一个不足近似记为 p n p_n pn,任意一个过剩近似值记为 q n q_n qn
- 当 p n , q n p_n,q_n pn,qn越来越接近 n n n时 a p n , a q n a^{p_n},a^{q_n} apn,aqn也就越 a n a^{n} an
- 即,我们可以用两个有理数幂的序列 { a p n } , { a q n } \set{a^{p_n}},\set{a^{q_n}} {apn},{aqn}无限逼近 a n a^{n} an
- 综上,一般的, a > 0 , ∀ α ∈ R a>0,\forall \alpha\in\mathbb{R} a>0,∀α∈R,实指数幂 a α a^{\alpha} aα就都有意义了,即正数的实指数幂都有意义
- 有理指数幂的运算法则也适用于无理数指数幂,即对实指数幂都适用
其他定义实指数的方法
- 方式1:因为所有实数可以近似地表示为有理数,任意实数指数x可以定义成: b x = lim r → x b r , b^x = \lim_{r \to x} b^r, bx=limr→xbr,
例如: x ≈ 1.732 x \approx 1.732 x≈1.732于是 5 x ≈ 5 1.732 = 5 433 250 = 5 433 250 ≈ 16.241 5^{x}\approx 5^{{1.732}}=5^{{{\frac {433}{250}}}}={\sqrt[ {250}]{5^{{433}}}}\approx 16.241 5x≈51.732=5250433=2505433≈16.241 - 方式2:实数指数幂通常使用对数来定义,而不是近似有理数。
- 自然对数 ln x \ln{x} lnx是指数函数 e x e^{x} ex的反函数。 它的定义是:对于任意 b > 0 b>0 b>0,满足 b = e ln b b = e^{\ln b} b=elnb
- 根据对数和指数运算的规则: b x = ( e ln b ) x = e x ⋅ ln b b^x = (e^{\ln b})^x = e^{x \cdot\ln b} bx=(elnb)x=ex⋅lnb
- 这就是实数指数幂的定义: b x = e x ⋅ ln b b^x = e^{x\cdot\ln b}\, bx=ex⋅lnb
- 实数指数幂 b x b^x bx的这个定义和上面使用有理数指数和连续性的定义相吻合。对于复数,这种定义更加常用。
特别的幂
- 0的正实指数幂为0;
- 0 0 0的负整数次幂无意义
- 0 0 0的0次幂可以定义为1,一种极限的看法: lim x → 0 + x x = 0 0 {\displaystyle \lim _{x\to 0^{+}}x^{x}=0^{0}} x→0+limxx=00
1的幂🎈
- 1的任何次幂都为1。
0的幂
- 0的正数幂都等于0。
- 0的负数幂没有定义。因为 0 − n = 1 0 n , n ∈ R + 0^{-n}=\frac{1}{0^{n}},n\in\mathbb{R^+} 0−n=0n1,n∈R+,这遇到了0作为除数的问题,因而未定义0的负指数幂
- 任何非0之数的0次方都是1;
- 而0的0次方是悬而未决的,
- 某些领域下常用的惯例是约定为1。
- 但某些教科书表示0的0次方为无意义。
- 也有人主张定义为1。
负1的幂
- -1的奇数幂等于-1
- -1的偶数幂等于1
幂的补充资料
-
来源是wikipedia,部分内容和前面章节重复
-
在数学中,重复连乘的运算叫做乘方,乘方的结果称为 幂[1](英语:mathematical power,power);由此,若 n n n 为正整数, n n n 个相同的数 b b b 连续相乘(即 b b b 自乘 n n n 次),就可将 b n {\displaystyle b^{n}} bn 看作乘方的结果 ——“幂”。
-
b n = b × ⋯ × b ⏟ n b^{n}=\underbrace {b\times \cdots \times b}_{n} bn=n b×⋯×b
-
幂运算(exponentiation)又称指数运算、取幂,是数学运算,表达式为 b n {\displaystyle b^{n}} bn,读作“ b b b 的 n n n 次方”或“ b b b 的 n n n 次幂”。
-
其中, b b b 称为底数,而 n n n 称为指数,通常指数写成上标,放在底数的右边。
-
当不能用上标时,例如在编程语言或电子邮件中, b n {\displaystyle b^{n}} bn 通常写成
b^n或b**n;也可视为超运算,记为b[3]n;亦可以用高德纳箭号表示法,写成 b↑n。 -
当指数为 1 时,通常不写出来,因为运算出的值和底数的数值一样;
-
指数为 2 时,可以读作“ b b b 的平方”;
-
指数为 3 时,可以读作“ b b b 的立方”。
-
由于在十进制中,10的幂很容易计算,只需在后面加零即可,所以科学记数法借此简化记录的数字;2的幂则在计算机科学中相当重要。
-
起始值 1(乘法的单位元)乘上底数( b b b)自乘指数( n n n)这么多次。这样定义了后,很易想到如何一般化指数 0 和负数的情况:
- 指数是零时,底数不为零,幂均为一(即除 0 外,所有数的 0 次方都是 1 );
- 指数是负数时,就等于重复除以底数(或底数的倒数自乘指数这么多次),即:
- b 0 = 1 ( b ≠ 0 ) {\displaystyle b^{0}=1\qquad (b\neq 0)} b0=1(b=0)
- b − n = 1 b × ⋯ × b ⏟ n = 1 b n = ( 1 b ) n ( b ≠ 0 ) {\displaystyle b^{-n}={1 \over \underbrace {b\times \cdots \times b} _{n}}={\frac {1}{b^{n}}}=\left({\frac {1}{b}}\right)^{n}\qquad (b\neq 0)} b−n=n b×⋯×b1=bn1=(b1)n(b=0)。
-
若以分数为指数的幂,则定义:
- b n m = b n m {\displaystyle b^{\frac {n}{m}}={\sqrt[{m}]{b^{n}}}} bmn=mbn,
- 即 b b b 的 n n n 次方再开 m m m 次方根。
-
0的0次方( 0 0 0^{0} 00)目前没有数学家给予正式的定义;
- 在部分数学领域中,如组合数学,常用的惯例是定义为 1 ,也有人主张定义为 1 。
- 此外,当 n n n 是复数,且 b b b 是正实数时, b n = exp ( n ln ( b ) ) {\displaystyle b^{n}=\exp(n\ln(b))} bn=exp(nln(b))
- exp 是指数函数,而 ln 是自然对数。
运算法则🎈
- 同底数幂相乘,底数不变,指数相加:
- a m × a n = a m + n a^m \times a^n = a^{m + n} am×an=am+n
- 同底数幂相除,底数不变,指数相减:
- a m ÷ a n = a m − n {\displaystyle a^{m}\div a^{n}=a^{m-n}} am÷an=am−n
- 同指数幂相除,指数不变,底数相除( b b b不为0):
- a n b n = ( a b ) n {\frac {a^{n}}{b^{n}}}=\left({\frac {a}{b}}\right)^{n} bnan=(ba)n
指数函数
- 一般地,函数 y = a x y=a^{x} y=ax, a > 0 , a ≠ 1 , x ∈ R a>0,a\neq{1},x\in{\mathbb{R}} a>0,a=1,x∈R
- 解析式中 a a a是非1的正数,不讨论负数
- 幂 a x a^{x} ax的底数为负数时,自变量 x x x的定义域将不连续
基本性质
- 定义域 D f D_f Df= R \mathbb{R} R,且 ∀ x ∈ R , y > 0 \forall{x}\in{\mathbb{R}},y>0 ∀x∈R,y>0,值域是 ( 0 , + ∞ ) (0,+\infin) (0,+∞)
- 函数图象在 x x x轴上且总是过 ( 0 , 1 ) (0,1) (0,1),因为 a 0 = 1 a^{0}=1 a0=1
- 当 a > 1 a>1 a>1这个函数是增函数,当 0 < a < 1 0<a<1 0<a<1时,函数是减函数
相关文章:

EM@基本初等函数@幂和根式@指数函数
abstract 基本初等函数幂和根式指数函数 指数和幂 正整指数幂 a n a^{n} an a ⋯ a ⏟ n 个 \underbrace{a\cdots{a}}_{n个} n个 a⋯a, n ∈ N n\in\mathbb{N^{}} n∈N 其中 a n a^{n} an称为** a a a的 n n n次幂** a a a叫做幂的底数, n n n叫做幂的指数 正整指数…...

时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测
时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测 目录 时序预测 | MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现NGO-GRU北方苍鹰算法优化门控循环单元时间序列预测&#…...

element 二次确认框,内容自定义处理
上代码: async inspectionTypeOff(row) {console.log(row.id);let taskArray await this.getTaskList(row.id); // 查询关联的任务console.log("taskArray", taskArray);let messageTip taskArray.length > 0? <div><p>确认禁用巡检项&…...

【软件设计师-中级——刷题记录4(纯干货)】
目录 进度管理工具Grantt图:程序语言基础:高级语言源程序模式: 每日一言:持续更新中... 个人昵称:lxw-pro 个人主页:欢迎关注 我的主页 个人感悟: “失败乃成功之母”,这是不变的道理…...

9.24 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表 1、自动驾驶一周资讯 - 小马智行在京开展“车内无人”出行服务商业化试点,余承东将升任车BU董事长 自动驾驶一周资讯 - 小马智行在京开展“车内无人”出行服务商业化试点࿰…...
持续更新)
第二章:25+ Python 数据操作教程(第二十五节用 PYTHON 和 R 制作祝福圣诞节)持续更新
这篇文章献给所有 Python 和 R 编程爱好者...通过以下程序在同行中炫耀您的知识。作为一名数据科学专业人士,您希望自己的愿望在圣诞节前夕变得特别。如果您观察代码,您还可以学到 1-2 个技巧,您可以在以后的日常任务中使用这些技巧。 方法 1:运行以下程序,看看我的意思 R…...
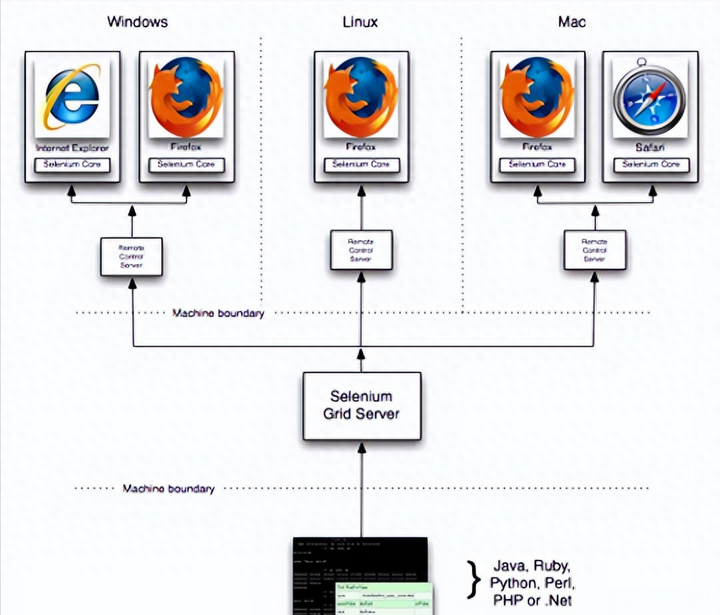
你是怎么理解自动化测试的?理解自动化测试的目的和本质
其实自动化测试很好理解,由两部分组成,“自动化”和“测试”,所以我们要理解自动化测试,就必须理解“自动化”和“测试”,只有理解了这些概念,才能更轻松的做好的自动化测试。其中“自动化”可以想象成通过…...

二十六、MySQL并发事务问题:脏读/不可重复读/幻读
1、事务的隔离级别 (1)隔离级别 Read uncommitted # 读,未提交 Read committed # 读,已提交 Repeatable Read(默认) # 可重复读 Serializable # 串读 (2)基础语法 set transaction isolation level 事…...

RK3588平台开发系列讲解(项目篇)视频监控之RTMP推流
文章目录 一、RTMP协议是什么二、RTMP 的原理三、Nginx 流媒体服务器四、FFmpeg 推流沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 目前常见的视频监控和视频直播都是使用了 RTMP、RTSP、HLS、MPEG-DASH、WebRTC流媒体传输协议等。 视频监控项目组成,分为三部分:…...
http基础教程(超详细)
HTTP HTTP 一 、基础概念 请求和响应报文URL 二、HTTP 方法 GETHEADPOSTPUTPATCHDELETEOPTIONSCONNECTTRACE 三、HTTP 状态码 1XX 信息2XX 成功3XX 重定向4XX 客户端错误5XX 服务器错误 四、HTTP 首部 通用首部字段请求首部字段响应首部字段实体首部字段 五、具体应用 连接管理…...

Vue3 <script setup> 单文件组件 组合式 API 相关语法
1.vue3使用vuex <script setup> import {ref} from "vue" import {useStore} from "vuex"//获取store const storeuseStore(); const count ref(0); //获取store状态 const type store.state.type //给count赋值 count.value1;</script>2.vue…...
为什么说网络安全是IT行业最后的红利?是风口行业?
前言 “没有网络安全就没有国家安全”。当前,网络安全已被提升到国家战略的高度,成为影响国家安全、社会稳定至关重要的因素之一。 网络安全行业特点 1、就业薪资非常高,涨薪快 2021年猎聘网发布网络安全行业就业薪资行业最高人均33.77万…...

DD5 进制转换
目录 一、题目 二、分析 三、代码 一、题目 进制转换_牛客题霸_牛客网 二、分析 三、代码 #include <iostream> #include <vector> #include <string> using namespace std; string Greater_than_Ten(int digit)//余数大于等于10的时候转换成对应的字母…...
之数据库提权-MySQL MOF提权)
操作系统权限提升(二十七)之数据库提权-MySQL MOF提权
MySQL MOF提权 MOF介绍 mof是windows系统的一个“托管对象格式”文件(位置:C:/windows/system32/wbem/mof/),其作用是每隔五秒就会去监控进程创建和死亡,mof目录下有两个文件夹(good与bad)。Windows server 2003及以下系统每5秒会执行一次mof目录下的文件,执行成功会…...

springcloud:四、nacos介绍+启动+服务分级存储模型/集群+NacosRule负载均衡
nacos介绍 nacos是阿里巴巴提供的SpringCloud的一个组件,算是eureka的替代品。 nacos启动 安装过程这里不再赘述,相关安装或启动的问题可以见我的另一篇博客: http://t.csdn.cn/tcQ76 单价模式启动命令:进入bin目录࿰…...
人生第一个java项目 学生管理系统
开始编程 建类 开始主要部分 main()部分 方法部分...

Oracle统计信息手动收集与修改
Oracle统计信息手动收集与修改 检查统计信息收集统计信息Schema统计信息收集表统计信息收集 修改统计信息锁定统计信息 检查统计信息 查看表统计信息是否过期: select owner,table_name,partition_name from dba_tab_statistics where STATTYPE_LOCKED is null a…...
鸿鹄工程项目管理系统 Spring Cloud+Spring Boot+Mybatis+Vue+ElementUI+前后端分离构建工程项目管理系统
. 项目背景 一、随着公司的快速发展,企业人员和经营规模不断壮大。为了提高工程管理效率、减轻劳动强度、提高信息处理速度和准确性,公司对内部工程管理的提升提出了更高的要求。 二、企业通过数字化转型,不仅有利于优化业务流程、提升经营管…...

ubuntu安装freeswitch 1.10.10
1、安装ffmpeg4.2 1.1、安装依赖库 sudo apt install yasm libogg-dev pkg-config libopus-dev libvpx-dev libx264-dev libx265-dev libfdk-aac-dev libsdl2-dev libfdk-aac-dev libmp3lame-dev libopencore-amrwb-dev libopencore-amrnb-dev libvorbis-dev libxvidcore-dev…...

什么类型的企业适合应用RPA?
在如今快速发展的商业环境中,企业不断面临挑战和机会。数字化转型不仅是一个选项,而是一个必要条件,尤其对于具有特定需求和挑战的企业来说。但究竟哪些类型的企业最适合通过RPA(Robotic Process Automation)进行数字化…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
