python 探索分形世界|曼德布洛特|np.frompyfunc()
文章目录
- 分形的重要特征
- 曼德布洛特集合
- 曼德布洛特集合有一个以证明的结论:
- 图像展示
- np.ogrid[]
- np.frompyfunc()
- 集合转图像
- julia集合
无边的奇迹源自简单规则的无限重复 ---- 分形之父Benoit B.Mandelbrot
分形的重要特征
- 自相似性
- 无标度性
- 非线性
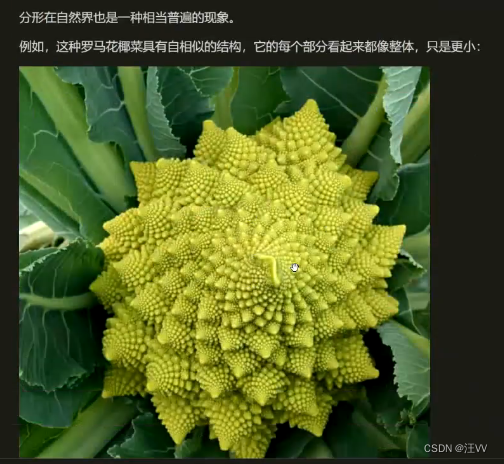
曼德布洛特集合
- z 0 = 0 z_0 = 0 z0=0
- z n + 1 = z n 2 + c z_{n+1} = z_{n}^2 + c zn+1=zn2+c
想要确定复数c是否属于曼德布洛特集合,只要将c代入上面公式,当n足够大时,如果序列没有发散,则说明c输入曼德布洛特集合。
def iter_m(c):z = cfor i in range(1, 10):z = z**2 + cprint(round(z, 3), end = '->')print('\n' + '*' * 20)
iter_m(-1)
iter_m(-0.5)
iter_m(0.5)# 输出
0->-1->0->-1->0->-1->0->-1->0->
********************
-0.25->-0.438->-0.309->-0.405->-0.336->-0.387->-0.35->-0.377->-0.358->
********************
0.75->1.062->1.629->3.153->10.444->109.567->12005.476->144131442.662->2.0773872763941816e+16->
********************
可以看到-1和0.5不收敛
从图像理解-0.5为什么收敛:
由 z n + 1 = z n 2 + c z_{n+1} = z_{n}^2 + c zn+1=zn2+c知道 z 1 = − 0.5 z_1 = -0.5 z1=−0.5, z 1 z_1 z1要作下一步的横坐标,因此由 y = x y =x y=x找到横坐标为 z 1 z_1 z1的点,然后再在曼德布洛特的迭代函数中计算。(win11的计算器绘图不是方格,我稍微查了一下也没找到解决办法,如果有人知道怎么改,希望能留言,感谢)可以看到收敛于交点,至于-1和0.5也可以用同样的方法从图中看出来。

曼德布洛特集合有一个以证明的结论:
复平面上的曼德布洛特集合在一个半径为2的圆内
# 改进后的函数
def iter_m3(c):z = cfor i in range(0, 200):if abs(z) > 2: # 迭代200次后还没有发散则说明很有可能就属于曼德布洛特集合return Falsez = z**2 + creturn True
图像展示
现提出想要对一个复数区域内的点进行区分是否属于曼德布洛特集合该如何做呢?
先学习两个方法
np.ogrid[]
x, y = np.ogrid[0:1:5j, -1:1:5j] # 前列后行
# 切片第三个参数如果以j结尾则是将其等分划分
# 如果没有j,只是一个数,则是以该数为间隔划分
print('x:\n', x)
print('y:\n', y)
z = x + y * 1j
print('z:\n', z)# 输出
x:[[0. ][0.25][0.5 ][0.75][1. ]]
y:[[-1. -0.5 0. 0.5 1. ]]
z:[[0. -1.j 0. -0.5j 0. +0.j 0. +0.5j 0. +1.j ][0.25-1.j 0.25-0.5j 0.25+0.j 0.25+0.5j 0.25+1.j ][0.5 -1.j 0.5 -0.5j 0.5 +0.j 0.5 +0.5j 0.5 +1.j ][0.75-1.j 0.75-0.5j 0.75+0.j 0.75+0.5j 0.75+1.j ][1. -1.j 1. -0.5j 1. +0.j 1. +0.5j 1. +1.j ]]
np.frompyfunc()
优点类似于map的功能,但不完全相同。对于上面的iter_m3()方法只能传入一个复数,如果传入一个包含复数的数组则不可以。为了解决这个问题,使用np.frompyfunc(func, nin, nout)
其中func是自定义函数,nin是传入参数的个数,nout是传出参数的个数。
mande = np.frompyfunc(iter_m3, 1, 1)
mande(z)# 输出
array([[True, True, True, True, True],[False, True, True, True, False],[False, False, False, False, False],[False, False, False, False, False],[False, False, False, False, False]], dtype=object)
同样也可以使用map达到该功能,但是复杂一些
result = np.array(list(map(lambda row: list(map(iter_m3, row)), z)))
# 注意:对于二维数组,一层map取的是一维数组
print(result)# 输出
[[ True True True True True][False True True True False][False False False False False][False False False False False][False False False False False]]
集合转图像
import numpy as np
import matplotlib.pylab as plt
from matplotlib import cmdef iter_m3(c):z = cfor i in range(0, 200):if abs(z) > 2: # 迭代200次后还没有发散则说明很有可能就属于曼德布洛特集合return Falsez = z**2 + creturn Truedef draw_set(cx, cy, d, ufunc:np.ufunc):x0, x1, y0, y1 = cx - d, cx + d, cy - d, cy + dy, x = np.ogrid[y0:y1:400j, x0:x1:400j]z = x + y * 1jplt.imshow(ufunc(z).astype(float), cmap=cm.jet, extent=[x0, x1, y0, y1])mande = np.frompyfunc(iter_m3, 1, 1)
draw_set(-0.5, 0, 1.5, mande)
输出图像:
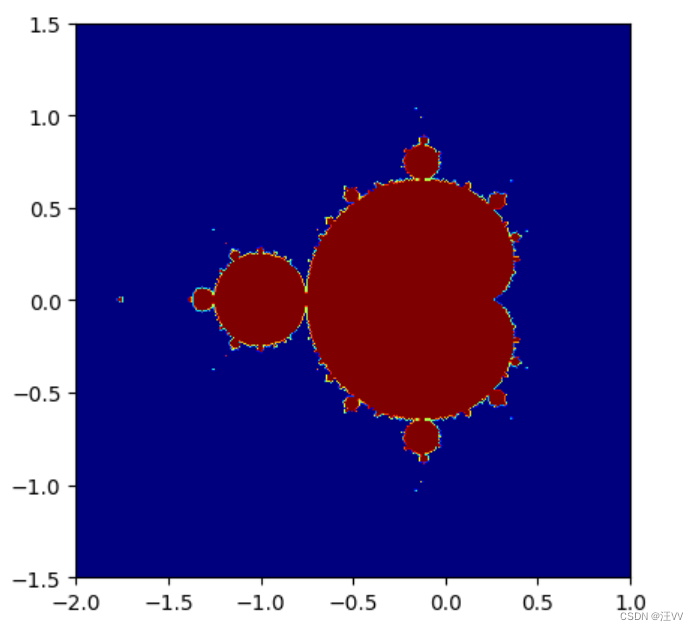
但是颜色不够鲜艳,希望每一个不同的发散点都能显示不同的颜色。
def iter_m4(c):z = cfor i in range(0, 200):if abs(z) > 2: # 迭代200次后还没有发散则说明很有可能就属于曼德布洛特集合breakz = z**2 + creturn i
mande = np.frompyfunc(iter_m4, 1, 1)
draw_set(-0.5, 0, 1.5, mande)
放大
对(0.273, 0.5921)处进行放大
x, y = 0.273, 0.5921
plt.subplot(2, 3, 1)
draw_set(-0.5, 0, 1.5, mande)
for i in range(2, 7):plt.subplot(2, 3, i)draw_set(x, y, 0.25**(i-1.5), mande)
输出:
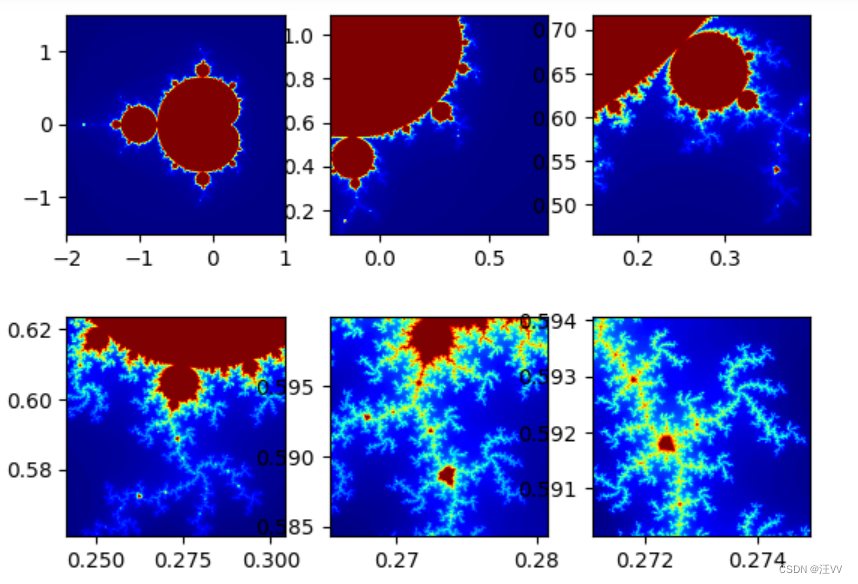
julia集合
迭代公式与曼德布洛特唯一区别在于 z 0 z_0 z0不是0,而是输入数据,c给定一个值,因此曼德布洛特集合只有一个,而julia集合有无数个。
def iter_j(z):c = -0.4 + 0.6jfor i in range(0, 200):if abs(z) > 2: # 迭代200次后还没有发散则说明很有可能就属于曼德布洛特集合breakz = z**2 + creturn i
julia = np.frompyfunc(iter_j, 1, 1)
draw_set(0, 0, 1.5, julia)
输出:
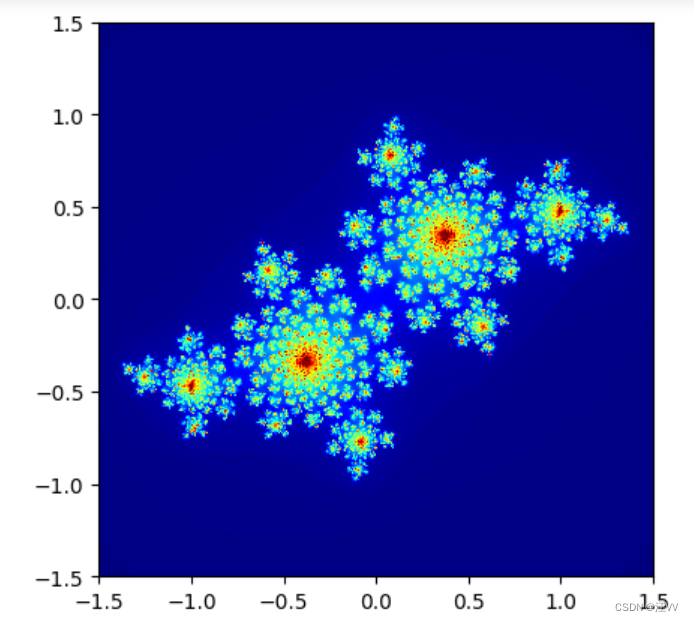
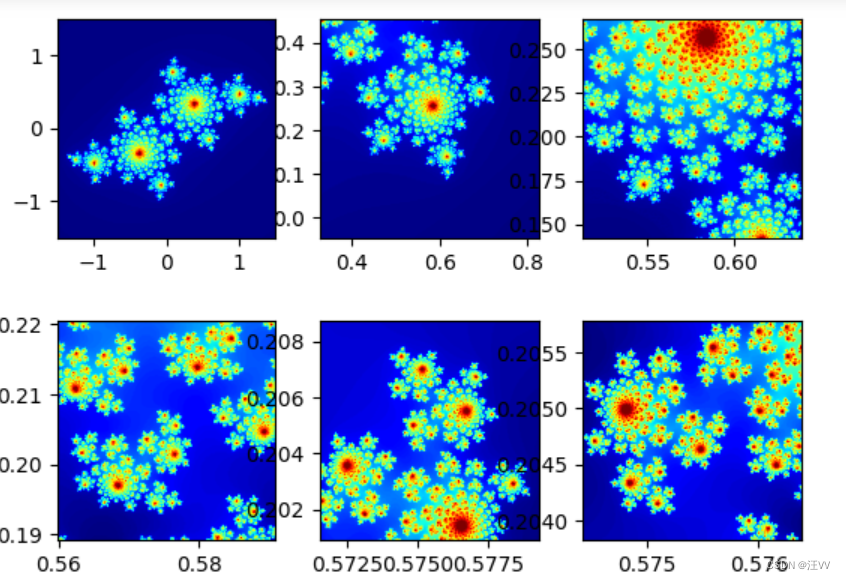
放大
x, y = 0.5754, 0.2048
plt.subplot(2, 3, 1)
draw_set(0, 0, 1.5, julia)
for i in range(2, 7):plt.subplot(2, 3, i)draw_set(x, y, 0.25**(i-1), julia)
输出:
相关文章:

python 探索分形世界|曼德布洛特|np.frompyfunc()
文章目录 分形的重要特征曼德布洛特集合曼德布洛特集合有一个以证明的结论:图像展示np.ogrid[]np.frompyfunc()集合转图像 julia集合 无边的奇迹源自简单规则的无限重复 ---- 分形之父Benoit B.Mandelbrot 分形的重要特征 自相似性无标度性非线性 曼德布洛特集合…...

Android MVVM示例项目
项目地址 GitHub - yaolunwei/Androidbbc at androidx 项目简介 BBC(基础业务组件) 业务组件的基础,所有业务组件必须基于该组件进行开发,提供一站式开发 快速使用 gradle: implementation com.bigoat.android:bbc:0.0.1 约定成俗 以下继承关系…...
迅为龙芯2K1000开发板通过汇编控制GPIO
上一小节,我们使用了 C 语言控制了 gpio,这一小节我们来看一下如何使用汇编来控制 gpio 呢?有的 同学可能会有疑问了,既然我们可以使用 C 语言来控制 gpio,为什么我们还要使用更底层的汇编语言呢, 如果我…...

合合信息、上海大学、华南理工大学发布业内首个古彝文编码“大字典” ,为古文字打造“身份证”
“乌蒙山连着山外山,月光洒向了响水滩。”近期在各大短视频平台爆火的《奢香夫人》你听过吗?奢香夫人是一位彝族“巾帼英雄”,这首同名歌曲早在2009年便已发布,如今突然“翻红”,不仅体现了大众对于少数民族文化高涨的…...

Django — 类视图和中间件
目录 一、类视图1、基于类的结构2、常见的类视图基类3、类视图的优点4、代码案例 二、中间件1、定义2、工作原理3、自带中间件4、中间件开发流程5、自定义中间件6、案例 一、类视图 类视图(Class-Based Views)是 Django 中用于处理 HTTP 请求和生成 HTT…...

VMware安装CentOS Stream 8以及JDK和Docker
一、下载镜像源 地址:https://developer.aliyun.com/mirror/?spma2c6h.25603864.0.0.285b32d48O2G8Y 二、安装配置 配置项 一共有以下这些,其中软件、软件选择 、安装目的地、网络主机名需要讲一下,其他都简单,自行设置即可。 …...
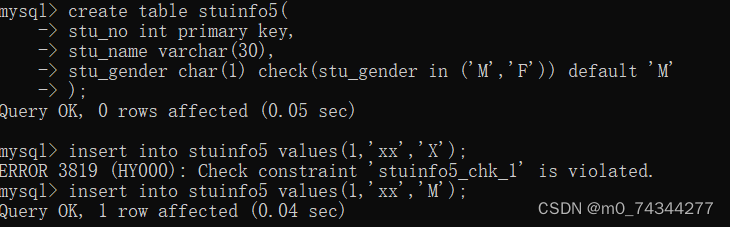
MySQL作业1
目录 一.创建一张表,包含以下所有数据类型 建表:编辑 二.使用以下六种约束 1.非空约束 2.唯一约束 3.主键约束 4.外键约束 5.检查约束 6.默认值约束 一.创建一张表,包含以下所有数据类型 Text 类型: Number 类型&#…...

基于微信小程序的家校通系统设计与实现(亮点:选题新颖、上传作业、批改作业、成绩统计)
文章目录 前言运行环境说明家长微信小程序端的主要功能有:教师微信小程序端的主要功能有:管理员的主要功能有:具体实现截图详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考论文…...
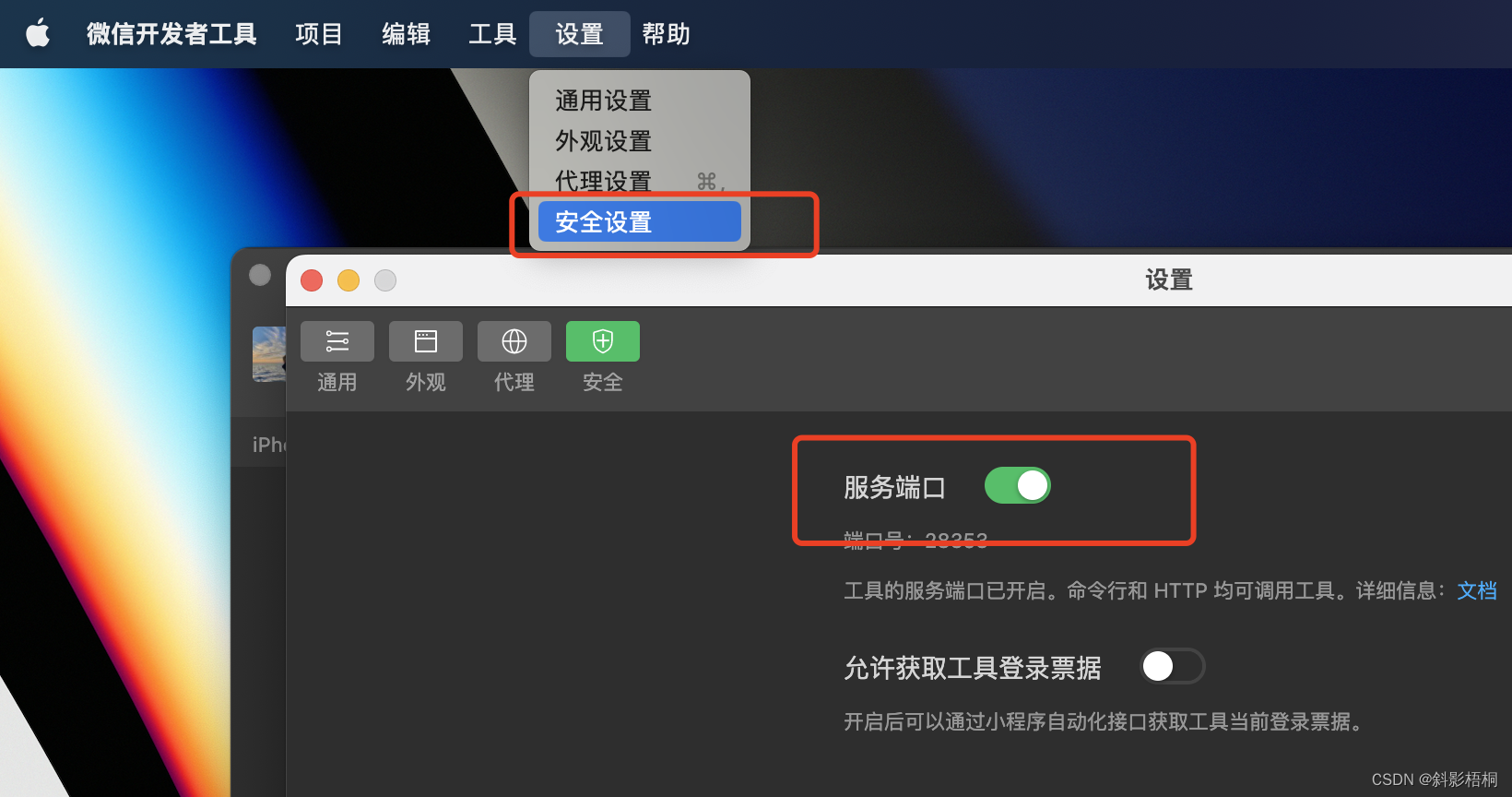
uni-app问题记录
一、启动问题记录 1. 报错1 解决办法: 开启微信开发者工具服务端口 2. 报错2:调用getLocation获取位置信息时报错以下内容 {errMsg: “getLocation:fail the api need to be declared in the requiredPrivateInfos field in app.json/ext.json”} 解决办法: manifest.json文…...

Leetcode---363周赛
题目列表 2859. 计算 K 置位下标对应元素的和 2860. 让所有学生保持开心的分组方法数 2861. 最大合金数 2862. 完全子集的最大元素和 一、计算k置为下标对应元素的和 简单题,直接暴力模拟,代码如下 class Solution { public:int sumIndicesWithKS…...

Netty粘包与拆包问题
先看一下下面的例子: 服务端代码为: public class TimeServer {public static void main(String[] args) throws InterruptedException {EventLoopGroup bossGroupnew NioEventLoopGroup();EventLoopGroup workerGroupnew NioEventLoopGroup();try{Serv…...

JS下载链接的两种方式
1、window.open() 弹出新窗口下载,需要用户进行交互之后触发,否则会被拦截,Safari始终会拦截弹窗 2、a标签下载 不会触发弹窗,更安全 let a document.createElement(a) a.href 下载链接; a.download 文件名称; document.bod…...
手把手教你实现:将后端SpringBoot项目部署到华为云服务器上
前言 前提:有一个后端项目,项目能够运行在本地,可以通过本地访问(localhost) 如果没有可以看这篇:一个基于SpringBoot的后端项目 注册华为云账号 华为云官网 购买云服务器 产品 -> 华为云耀云服务器…...
【红队攻防】从零开始的木马免杀到上线
0、环境配置说明 应该全部使用云服务器完整演示比较好,奈何太穷了买不起服务器,只能用本地环境演示。所需环境如下: 系统环境: CentOS 7 ,Windows 10 软件环境 Cobalt Strike 4.7 , ShellQMaker, 360杀…...

Linux命令行操作:使用“more“命令进行分页显示
文章目录 1. 引言1.1 介绍Linux操作系统和命令行界面什么是Linux操作系统?为什么命令行界面在Linux中如此重要? 1.2 介绍Linux中的分页显示命令分页显示命令的作用与意义不同分页显示命令的比较 2. "more"命令的基本用法2.1 安装和启动"m…...
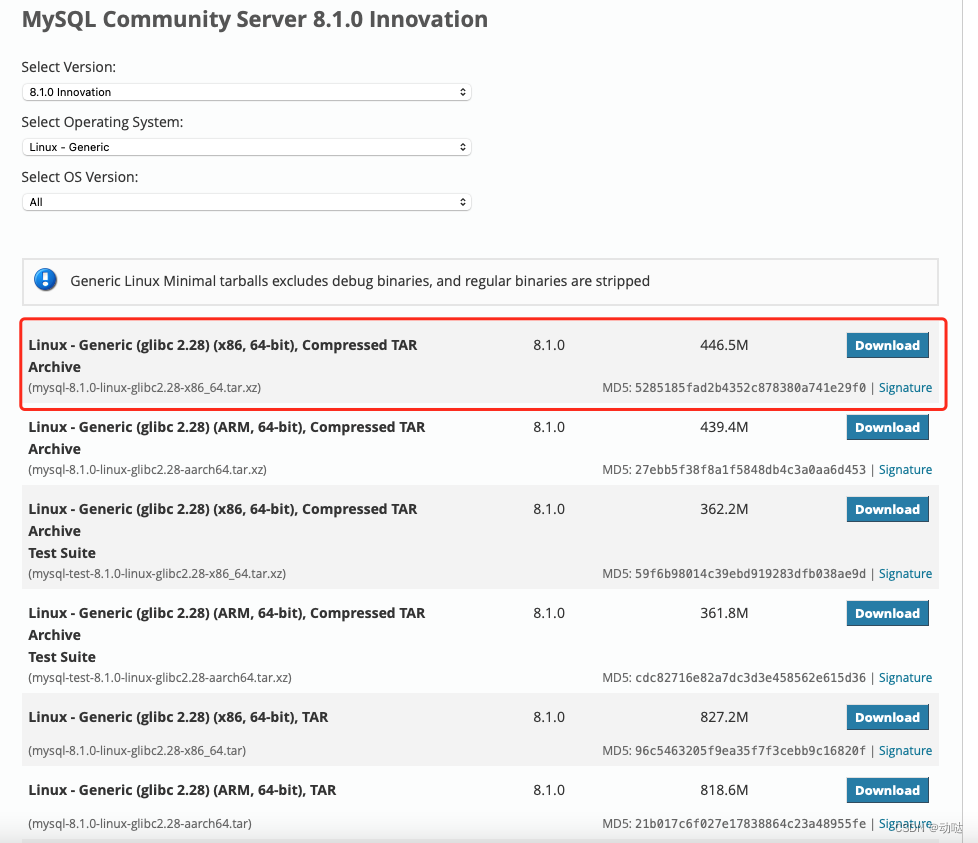
CentOS下安装MySQL 8.1及备份配置
1 卸载原来的MySQL版本 移除之前部署的mysql软链接 # unlink /etc/init.d/mysql # unlink /usr/bin/mysql2 下载最新的MySQL版本 https://dev.mysql.com/downloads/mysql/8.0.html 我这里直接把地址放在这里:https://cdn.mysql.com//Downloads/MySQL-8.1/mysql…...
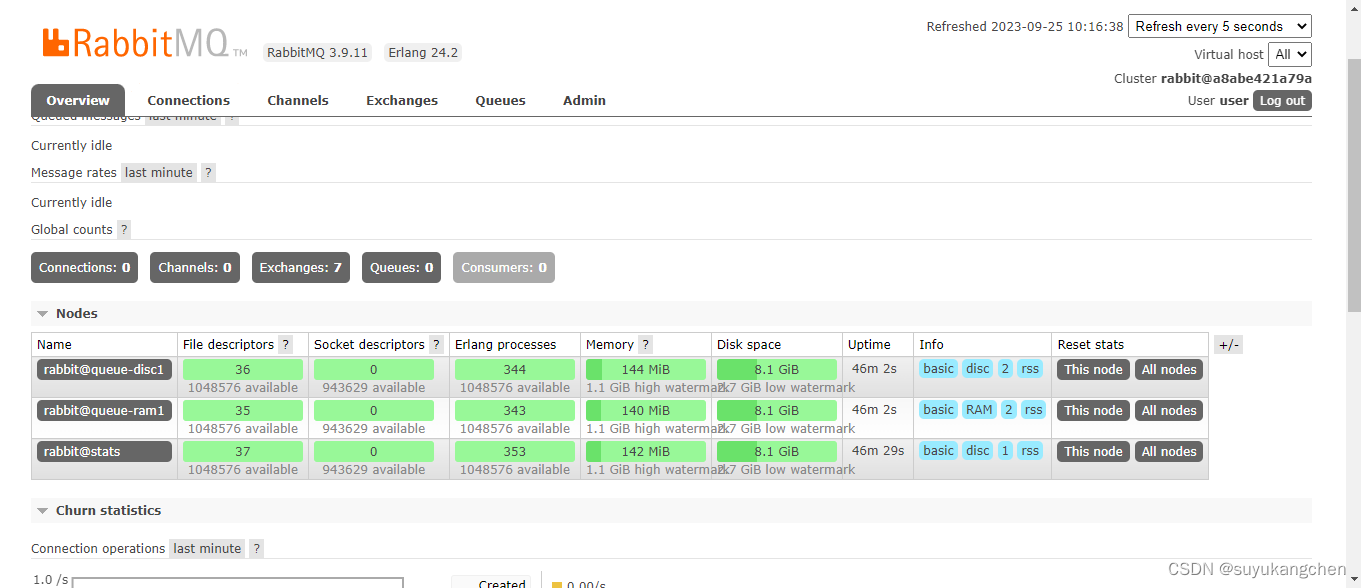
【RabbitMQ实战】06 3分钟部署一个RabbitMQ集群
一、集群的安装部署 我们还是利用docker来安装RabbitMQ集群。3分钟安装一个集群,开始。 前提条件,docker安装了docker-compose。如果没安装的话,参考这里 docker-compose文件参考bitnami官网:https://github.com/bitnami/contai…...
整形提升)
(c语言)整形提升
#include<stdio.h> //整形提升 int main() { char a 5; //字符型的内存大小为8个比特位,故在进行加法之类的线性运算时需要整形提升 //00000000000000000000000000000101->5 因为字符型的内存大小不足,故在存放整形时需要裁切 …...

上传文件报错:The temporary upload location [/tmp/tomcat/xxx] is not valid
1.上传附加时报错找不到临时目录 Failed to parse multipart servlet request; nested exception is java.io.IOException: The temporary upload location [/tmp/tomcat/work/Tomcat/localhost/ROOT] is not valid 发生改报错原因为 (1)、SpringBoot项目启动后,系…...

直线模组的品牌有哪些?
中国工业制造业快速发展,工业自动化领域也进入了飞速发展的阶段,直线模组作为工业自动化领域不可缺少的机器人之一,有着重要的不可或缺的作用,在行业内做得好的直线模组品牌有哪些呢? 1、NSK:日本精工株式会…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
