扩展欧几里得
扩展欧几里得算法
求 a x + b y = d ax+by=d ax+by=d 的一组解, d = gcd ( a , b ) d = \gcd(a,b) d=gcd(a,b)。
辗转相除递归求解。
假设已经求出 b x + ( b m o d a ) y = d bx + (b \bmod a)y = d bx+(bmoda)y=d 的一组解。
a x + b y = b x ′ + ( b m o d a ) y ′ = b x ′ + ( b − b × ⌊ a b ⌋ ) y ′ = a y ′ + b ( x ′ − ⌊ a b ⌋ y ′ ) ax+by=bx'+(b\bmod a)y'\\ =bx'+(b-b \times \lfloor\frac{a}{b} \rfloor)y'\\ =ay'+b(x'- \lfloor\frac{a}{b}\rfloor y') ax+by=bx′+(bmoda)y′=bx′+(b−b×⌊ba⌋)y′=ay′+b(x′−⌊ba⌋y′)
则 x = y ′ , y = x ′ − ⌊ a b ⌋ y ′ x = y', y = x' - \lfloor\frac{a}{b} \rfloor y' x=y′,y=x′−⌊ba⌋y′。递归计算即可。 b = 0 b = 0 b=0 时,由辗转相除得 a = d a = d a=d,则 x = 1 , y = 0 x=1,y=0 x=1,y=0 显然是一组解。
void exgcd(int a, int b, int &x, int &y)
{if(b == 0) return x = 1, y = 0, void();exgcd(b, b%a, y, x), y -= (a / b) * x;
}
扩欧求逆元
求 a a a 在模 p p p 下得逆元,等价于求 a x ≡ 1 ( m o d p ) ax \equiv 1 \pmod p ax≡1(modp),等价于 a x + p y ≡ 1 ( m o d p ) ax +py \equiv 1 \pmod p ax+py≡1(modp)。 gcd ( a , p ) = 1 \gcd(a,p)=1 gcd(a,p)=1 时才有解,即 a a a 有逆元。
裴属定理
我们对问题加以扩展,求解 a x + b y = c ax + by = c ax+by=c。
裴属定理:方程有解当且仅当 gcd ( a , b ) ∣ c \gcd(a,b) \mid c gcd(a,b)∣c。
若方程有解,则用扩欧求出 a x + b y = d ax + by = d ax+by=d 对一组特解后乘以 c d \frac c d dc 即可(由裴属定理得 c d \frac c d dc 为整数)。
再找出特解后,加上 a x + b y = 0 ax+by=0 ax+by=0 的解即可得到该不定方程的通解。
相关文章:

扩展欧几里得
扩展欧几里得算法 求 a x b y d axbyd axbyd 的一组解, d gcd ( a , b ) d \gcd(a,b) dgcd(a,b)。 辗转相除递归求解。 假设已经求出 b x ( b m o d a ) y d bx (b \bmod a)y d bx(bmoda)yd 的一组解。 a x b y b x ′ ( b m o d a ) y ′ b x …...
)
MySQL 事务介绍 (事务篇 一)
什么是事务? 事务是一组操作的集合,它是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。 注意点:默认MySQL的事务是自动提交…...

nvm nodejs的版本管理工具
nvm 全英文名叫 node.js version management,是一个 nodejs 的版本管理工具,为了解决 nodejs 各种版本存在不兼容现象可以通过他安装和切换不同版本的 nodejs。 一、完全删除之前的 node 和 npm 1. 打开 cmd 命令窗口,输入 npm cache clean…...
terraform简单的开始-vpc cvm创建
从网络开始 从创建VPC开始 复用前面的main.tf的代码: terraform {required_providers {tencentcloud {source "tencentcloudstack/tencentcloud"version "1.81.25"}} } variable "region" {description "腾讯云地域"…...
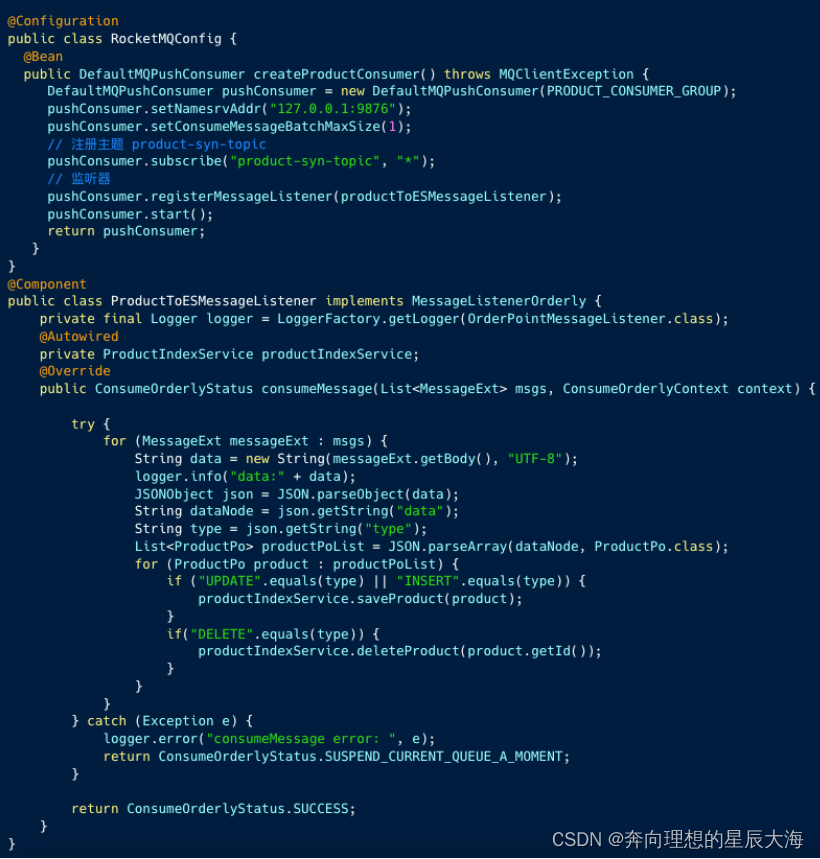
【MySQL】开启 canal同步MySQL增量数据到ES
开启 canal同步MySQL增量数据到ES canal 是阿里知名的开源项目,主要用途是基于 MySQL 数据库增量日志解析,提供增量数据订阅和消费。示使用 canal 将 MySQL 增量数据同步到ES。 一、集群模式 图中 server 对应一个 canal 运行实例 ,对应一…...
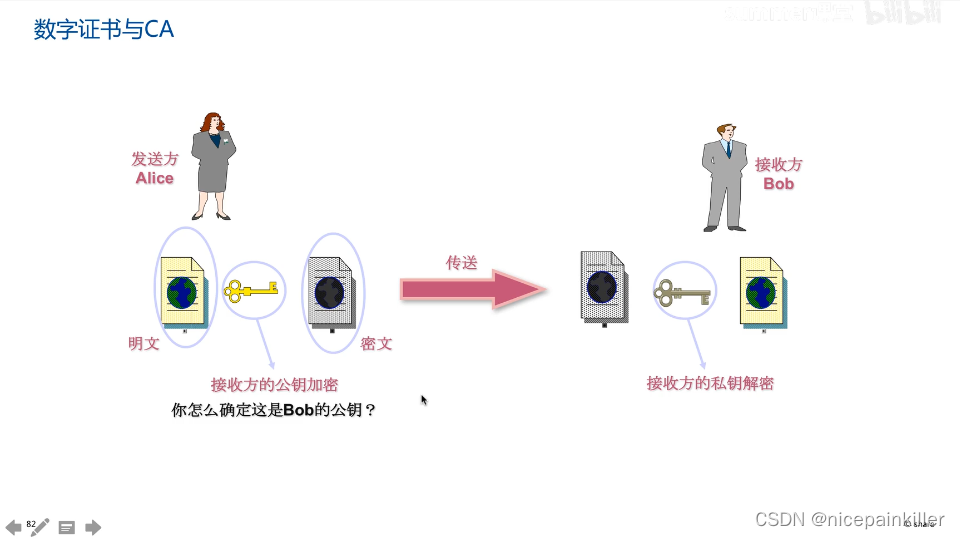
密码学概论
1.密码学的三大历史阶段: 第一阶段 古典密码学 依赖设备,主要特点 数据安全基于算法的保密,算法不公开,只要破译算法 密文就会被破解, 在1883年第一次提出 加密算法应该基于算法公开 不影响密文和秘钥的安全ÿ…...

渗透测试中的前端调试(一)
前言 前端调试是安全测试的重要组成部分。它能够帮助我们掌握网页的运行原理,包括js脚本的逻辑、加解密的方法、网络请求的参数等。利用这些信息,我们就可以更准确地发现网站的漏洞,制定出有效的攻击策略。前端知识对于安全来说,…...
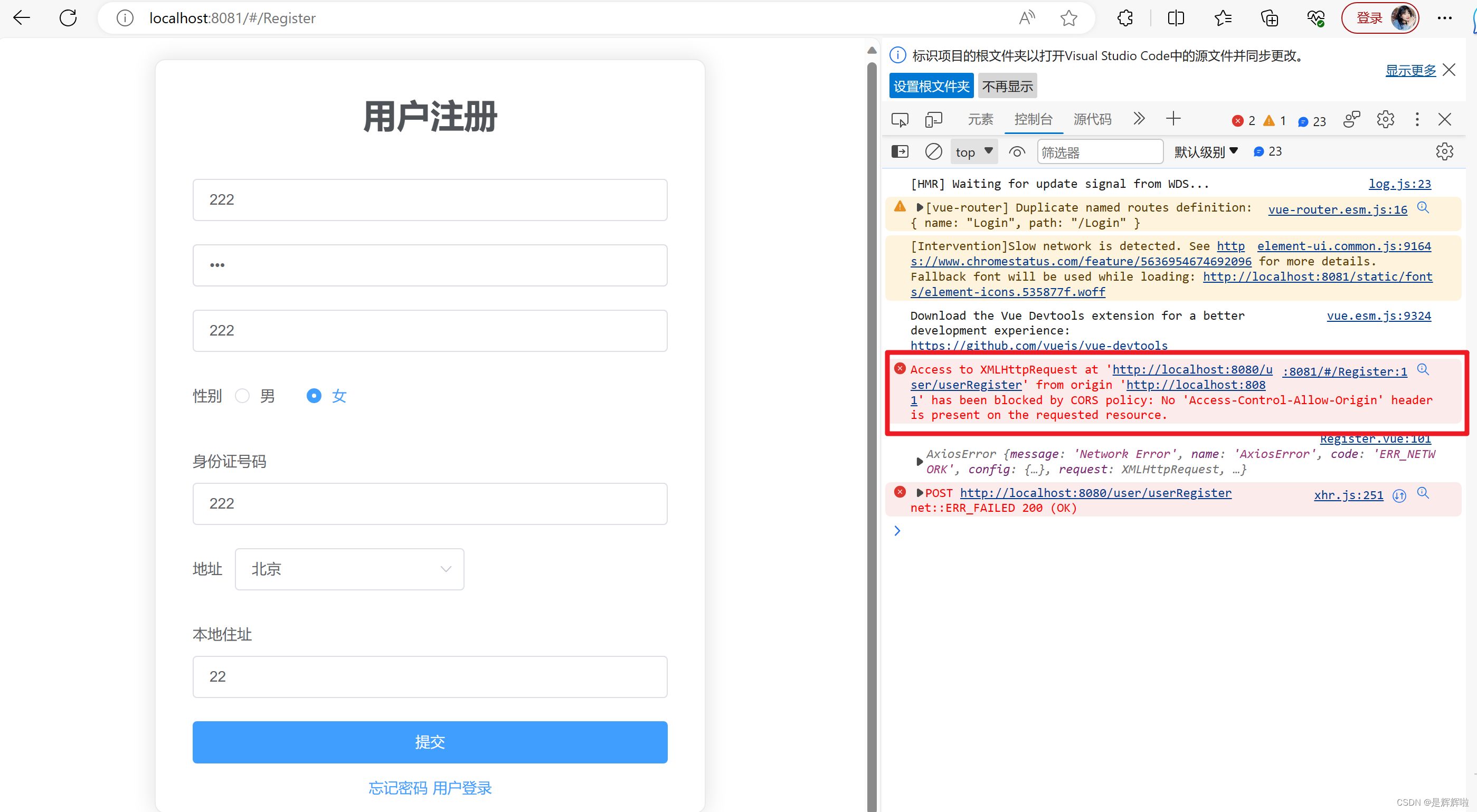
SPA项目之登录注册--请求问题(POSTGET)以及跨域问题
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于VueElementUI的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.ElementUI是什么 💡…...

Spring Cloud Alibaba Gateway全局token过滤、局部过滤访问时间超过50ms日志提示
文章目录 Spring Cloud Alibaba Gateway验证token在前篇的基础上加入依赖在filter包中创建tokenFilter Spring Cloud Alibaba Gateway局部过滤1.继承AbstractGatewayFilterFactory2.仿照AddRequestHeaderGatewayFilterFactory Spring Cloud Alibaba Gateway验证token 基础搭建…...

运算符 - Go语言从入门到实战
运算符 - Go语言从入门到实战 算术运算符 假设A变量等于10,B变量等于20。 运算符描述实例相加A B 输出结果 30-相减A - B 输出结果 -10*相乘A * B 输出结果 200/相除B / A 输出结果 2%求余B % A 输出结果 0⾃增A 输出结果 11–⾃减A-- 输出结果 9 特性…...

jupyterlab开发环境最佳构建方式
文章目录 背景jupyterlab环境构建运行虚拟环境构建以及kernel映射验证总结 背景 从jupyter notebook切换到了jupyter lab. 这里记录一下本地环境的最佳构建方式. jupyter lab 安装在jupyterlab-local的anaconda 虚拟环境中.建立多个其他虚拟环境安装各种python包实现环境隔离,…...
Qt_C++读写NFC标签Ntag支持windows国产linux操作系统
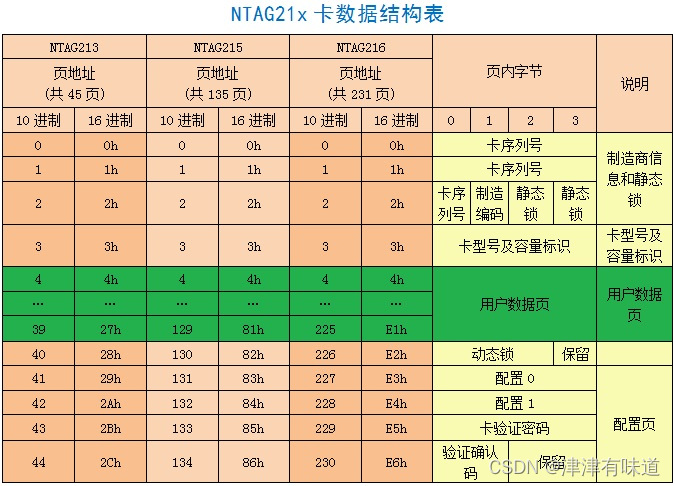
本示例使用的发卡器:Android Linux RFID读写器NFC发卡器WEB可编程NDEF文本/智能海报/-淘宝网 (taobao.com) ntag2标签存储结构说明 #include "mainwindow.h" #include "./ui_mainwindow.h" #include <QDebug> #include "QLibrary&…...

Web开发-基础知识扫盲
目录 Web 服务器Web 服务器例子 MVC架构Web 项目运行过程负载均衡和反向代理持久化Java对象JPA Web 服务器 Web 服务器是一种计算机程序,它通过 HTTP 协议接收和响应客户端发送的请求。Web 服务器将 HTML、CSS、JavaScript 和其他资源文件发送给客户端,…...

SpringMVC 学习(四)RestFul 风格
5. RestFul 风格 5.1 简介 概念 Restful就是一个资源定位及资源操作的风格。不是标准也不是协议,只是一种风格。基于这个风格设计的软件可以更简洁,更有层次,更易于实现缓存等机制。 功能 资源:互联网所有的事物都可以被抽象为…...

消息中间件相关知识
1、概述 消息队列已经逐渐成为企业IT系统内部通信的核心手段。它具有低耦合、可靠投递、广播、流量控制、最终一致性等一系列功能,成为异步RPC的主要手段之一。当今市面上有很多主流的消息中间件,如老牌的ActiveMQ、RabbitMQ,炙手可热的Kafka…...

JackJson多态
JsonTypeInfo 处理多态、序列化对象类型_赵丙双的博客-CSDN博客 JsonTypeInfo实现jackson的多态解析_MonkeyKing_sunyuhua的博客-CSDN博客 Java Jackson JsonTypeInfo 多态类型处理 - 简书 JsonTypeInfo 逻辑名称 JsonSubTypes、JsonTypeName_赵丙双的博客-CSDN博客...

孟晚舟最新发声!华为吹响人工智能的号角,发布“全面智能化”战略部署
原创 | 文 BFT机器人 1、华为孟晚舟新发声,华为发布“全面智能化”战略 上周三(9月30号)上午,华为全联接大会2023正式在上海举行,作为华为副董事长、轮值董事长、CFO的孟晚舟代表华为再次发声!在演讲上&am…...
open62541开发:添加sqlite3 历史数据库
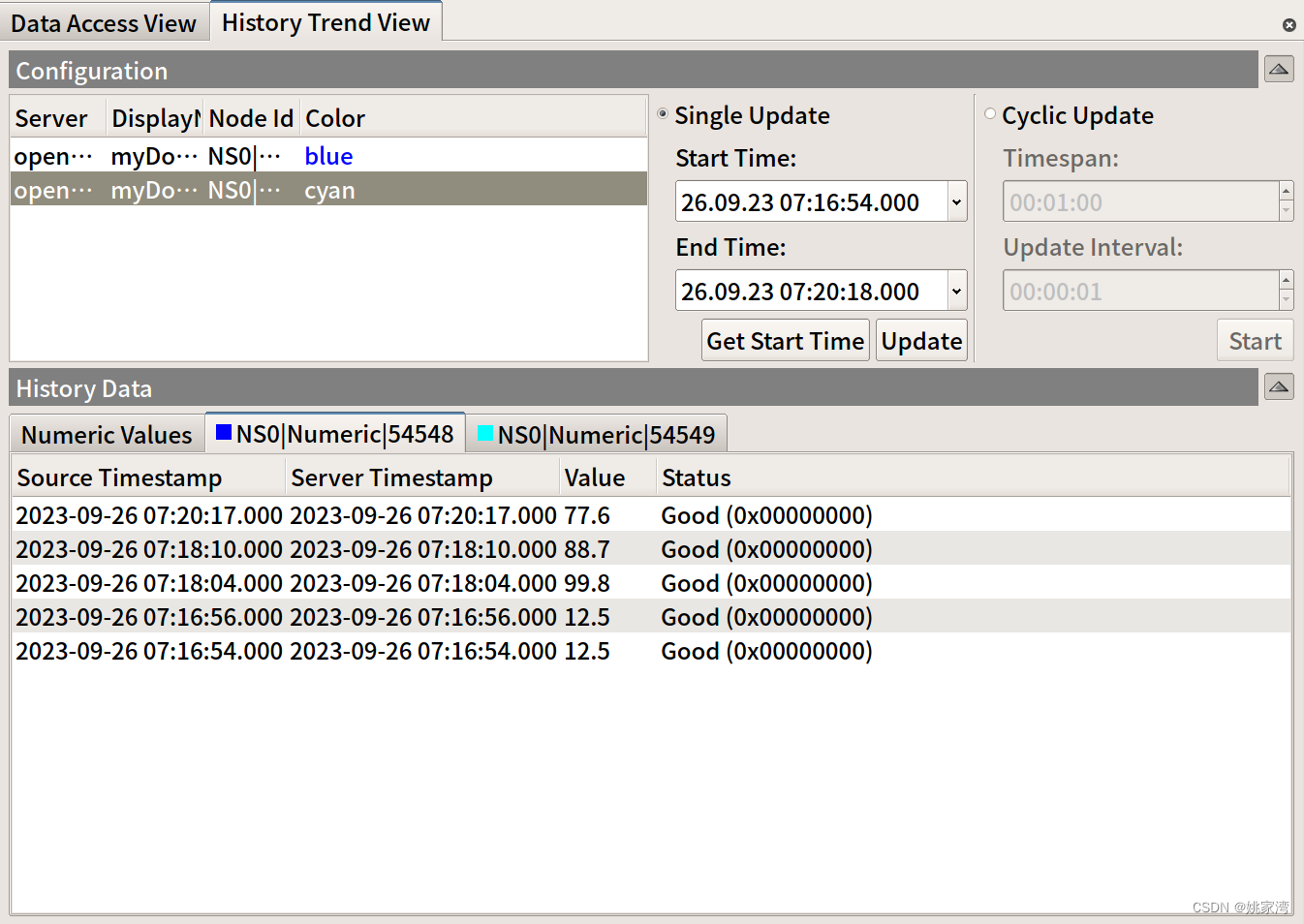
历史数据库在OPCUA 应用中十分重要,例如OPCUA 网关和OPCUA 汇聚服务器中都需要历史数据库功能。但是open62541 协议栈中仅包含了基于内存的历史数据库,在实际应用中是不够的。本博文讨论open62541 中添加sqlite3 为基础的历史数据库若干问题。 借鉴 Gi…...
美国零售电商平台Target,值得入驻吗?如何入驻?
Target 是美国最大的零售商之一,在品牌出海为大势所趋的背景下,它在北美电商中的地位节节攀升。Target 商店在众多垂直领域提供各种价格实惠的自有品牌,吸引越来越多的跨境商家入驻,如美妆、家居、鞋服、日用百货等,随…...

docker freeswitch mysql驱动相关
1. docker环境 的freeswitch要连mysql数据库 2. centos版本:7.9 3. mysql版本:mysql8.0 4. odbc版本:适用以下命令查询 rpm -qa | grep -E "unixODBC|mysql-connector-odbc" mysql-connector-odbc-5.2.5-8.el7.x86_64 unixODB…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
