【算法】分治法
文章目录
- 概念
- 原理和步骤
- 代码示例
- 总结
概念
分治法(Divide and Conquer)是一种算法设计策略,其思想是将一个大问题划分为若干小规模的子问题,然后递归地解决每个子问题,并将它们的解合并起来以得到原始问题的解。分治法包含三个基本步骤:分解、解决和合并。
分解(Divide):将原始问题划分为若干个规模较小且相互独立的子问题。这个步骤通常通过递归地将问题分解为更小的子问题来实现。分解的过程要求每个子问题的规模都比原始问题的规模小,且子问题之间没有重叠。
解决(Conquer):递归地解决每个子问题。当子问题足够小,可以直接求解时,可以采用基本的求解方法或直接返回已知的解。
合并(Combine):将子问题的解合并起来,得到原始问题的解。这个步骤通常是将各个子问题的解组合成原问题的解。在合并的过程中,可能需要进行一些额外的计算或操作。
分治法的核心思想是将复杂的问题分解为一系列相对简单的子问题,然后通过递归地求解子问题,最终将子问题的解合并起来得到原始问题的解。该算法设计策略通常用于解决一些具有重复性结构的问题,如排序、查找、图搜索等。通过将大问题划分为小问题,并使用递归思想求解,可以降低问题的复杂度,提高算法的效率。
值得注意的是,分治法在应用时需要满足以下两个基本要求:子问题的规模较小且相互独立,以及问题的结构具有递归性质。只有满足这两个要求,分治法才能够发挥其优势并得到正确的解。
原理和步骤
当使用分治法解决问题时,我们遵循以下详细步骤:
分解(Divide):将原始问题划分为若干个规模较小且相互独立的子问题。这个步骤的关键是找到一种方法将大问题划分为小问题,确保子问题的规模比原问题更小,并且子问题之间没有重叠。
解决(Conquer):递归地求解每个子问题。每个子问题的解可以通过直接求解或进一步分解为更小的子问题来获得。如果子问题足够小,可以使用基本的解决方法或直接返回已知的解。
合并(Combine):合并子问题的解来获得原始问题的解。在这个步骤中,我们将子问题的解合并起来,通常需要进行一些额外的计算或操作。
下面我们以计算数组中元素和的问题为例来详细说明分治法的原理。
假设我们有一个数组,我们想要计算数组中所有元素的和。
分解(Divide):将数组划分为两个部分,每个部分包含大约一半的元素。例如,将数组从中间位置拆分成两个子数组。
解决(Conquer):递归地对每个子数组进行求和。如果子数组足够小,我们可以直接对每个子数组进行求和并返回结果。
合并(Combine):将子数组的和相加以获得原始数组的总和。在这个例子中,我们只需将两个子数组的和相加即可得到原始数组的总和。
通过以上步骤,我们就成功地使用分治法解决了计算数组元素和的问题。
需要注意的是,对于某些情况下,我们可能需要考虑优化合并操作的方法。例如,在归并排序算法中,我们可以使用合并操作的线性时间复杂度的方法来优化整体算法的效率。
分治法是一种将大问题划分为小问题、递归地求解子问题并合并子问题解的算法设计策略。它的基本步骤包括分解、解决和合并。分治法的核心思想在于将问题划分为规模更小且相互独立的子问题,并通过递归地求解每个子问题来最终解决原始问题。通过合理地应用分治法,我们可以提高算法的效率并解决各种复杂的问题。
代码示例
public class DivideAndConquer {public static int sum(int[] nums) {return sumHelper(nums, 0, nums.length - 1);}private static int sumHelper(int[] nums, int start, int end) {if (start == end) { // 基本情况:只有一个元素return nums[start];} else {int mid = (start + end) / 2; // 求中间位置int leftSum = sumHelper(nums, start, mid); // 递归求左半部分的和int rightSum = sumHelper(nums, mid + 1, end); // 递归求右半部分的和return leftSum + rightSum; // 合并左右两部分的和}}public static void main(String[] args) {int[] nums = {1, 2, 3, 4, 5};int totalSum = sum(nums);System.out.println("数组的和为:" + totalSum);}
}在上述代码中,sum 函数是调用方接口,用户只需传入整数数组,然后调用 sumHelper 函数进行辅助计算。sumHelper 函数是实际的递归函数,它根据传入的起始位置 start 和结束位置 end 来确定当前子问题的规模。
在 sumHelper 函数中,首先判断基本情况,即子数组只有一个元素时直接返回该元素的值。否则,通过求取中间位置 mid 将问题分解为两个较小的子问题,分别递归地计算左半部分和右半部分的和。最后,将左右两部分的和相加得到原始数组的总和。
在 main 函数中,我们创建一个示例数组 nums,然后调用 sum 函数计算数组的和,并打印结果。
运行该代码,输出结果为:数组的和为:15
总结
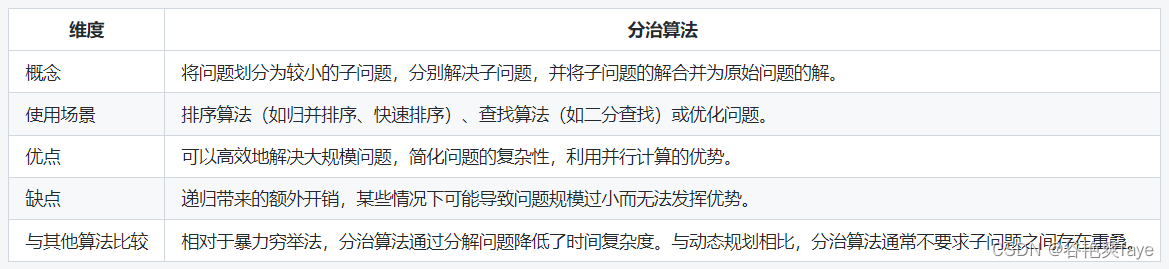
分治算法通过将问题划分为较小的子问题来解决复杂问题。它通常用于排序和查找问题,以及一些优化问题。分治算法的优点包括可以高效地解决大规模问题,简化问题的复杂性,并利用并行计算的优势。然而,分治算法的缺点在于递归过程中可能带来额外的开销,并且在某些情况下问题规模过小无法发挥优势。与暴力穷举法相比,分治算法通过分解问题降低了时间复杂度。与动态规划相比,分治算法通常不要求子问题之间存在重叠。
请注意,这只是一个简单的表格分析,实际上,随着问题的不同,分治算法的使用场景、优缺点等方面可能会有所变化。因此,在实际应用中,需要根据具体情况进行进一步评估和分析。
相关文章:

【算法】分治法
文章目录 概念原理和步骤代码示例 总结 概念 分治法(Divide and Conquer)是一种算法设计策略,其思想是将一个大问题划分为若干小规模的子问题,然后递归地解决每个子问题,并将它们的解合并起来以得到原始问题的解。分治…...
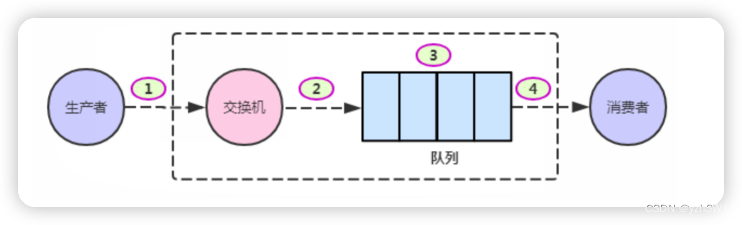
Rabbit消息的可靠性
生产者重连 消费者重试 Confirm模式简介 消息的confirm确认机制,是指生产者投递消息后,到达了消息服务器Broker里面的exchange交换机,则会给生产者一个应答,生产者接收到应答,用来确定这条消息是否正常的发送到Broker…...

Java中的网络编程是什么?
Java中的网络编程是指使用Java编程语言进行网络通信的过程和技术。它允许Java程序在互联网或局域网上进行数据交换、通信和传输。 Java提供了许多类和接口,用于实现网络编程。主要的网络编程相关的类在java.net包中可以找到。以下是一些常用的类和接口:…...

Oracle 常用命令大全
数据库 ----数据库启动 & 关闭 启动数据库 SQL> startup nomount; SQL> alter database mount; SQL> alter database open;关闭数据库 SQL> shutdown immediate;更多内容请参考:Oracle数据库启动和关闭 ----连接数据库 登陆普通用…...

Mysql 开启ssl连接
本文是针对Mysql 5.7版本以上数据库 1. 检查当前SSL / TLS状态 我们将使用-h指定IPv4本地环回接口,以强制客户端与TCP连接,而不是使用本地套接字文件。 这将允许我们检查TCP连接的SSL状态: mysql -u root -p -h 127.0.0.1键入以下内容以显示SSL / TLS变量的状态: SHOW …...

Java Stream流对List集合进行分页
有一种情况,我们有时不便在数据库层面进行分页。我们知道Mybatis的startPage();方法也是对数据库进行limit操作,有没有一种方式,只对List集合进行分页呢? 当然有,我们可以使用Stream流的方式对List集合进行操作&#…...
Docker(二)、linux环境Docker的部署以及构建镜像
linux环境Docker的部署以及构建镜像 一、docker部署1、快速部署常用的命令:1.1、demo-部署tomcat1.2、tomcat容器内部结构1.2.1、每个tomcat容器,都包含三个组件1.2.2、在容器内部执行命令 1.3、容器生命周期 二、Dockerfile构建镜像1、demo-Dockerfile自…...
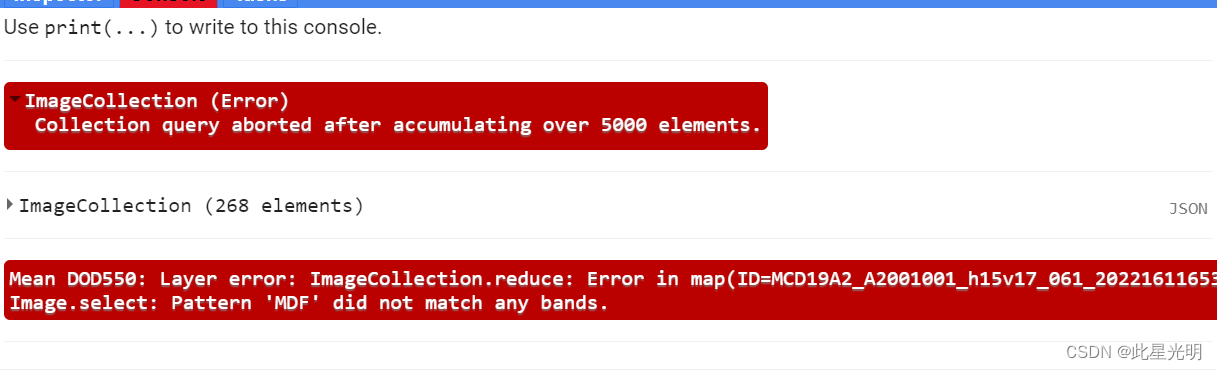
GEE错误——Image.select: Pattern ‘MDF‘ did not match any bands
问题 ImageCollection (Error) Collection query aborted after accumulating over 5000 elements. ImageCollection (268 elements) Mean DOD550: Layer error: ImageCollection.reduce: Error in map(ID=MCD19A2_A2001001_h15v17_061_2022161165308_01): Image.select: Patte…...

前端JavaScript入门到精通,javascript核心进阶ES6语法、API、js高级等基础知识和实战 —— JS基础(四)
开始吧,做时间的主人! 把时间分给睡眠,分给书籍,分给运动, 分给花鸟树木和山川湖海, 分给你对这个世界的热爱, 而不是将自己浪费在无聊的人和事上。 思维导图 函数 为什么需要函数 <!DO…...
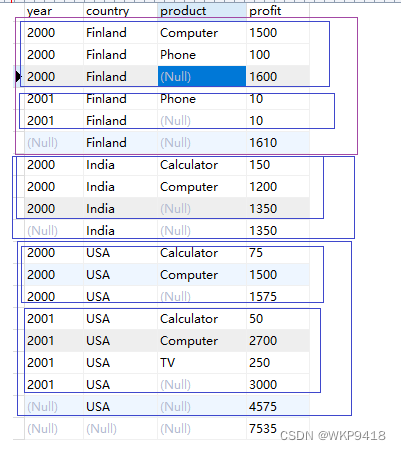
mysql超级聚合with rollup
超级聚合,是在group by的基础上,再次进行聚合。 它再次聚合的列,是select中没有用到聚合函数的列。 文章目录 例子1解释例子2表以及数据 例子1 mysql> SELECT year, country, product, SUM(profit) AS profitFROM salesGROUP BY year, c…...

浅谈电动汽车充电桩设计与应用研究
安科瑞 华楠 摘要:目前,随着我国社会经济的快速发展,我国的各个领域都取得了突破性的发展,尤其是在电动汽车充电桩的设计方法,新型的电动汽车充电桩设计已经广泛的受到了人民群众的青睐与认可,而这种发展前…...

tensorflow Windows安装说明
TensorFlow官网教程 Tensorflow 2.10是最后一个在本地windows上支持GPU的版本。从2.11版本开始,需要在windows WLS2(适用于 Linux 的 Windows 子系统)上安装才能使用GPU。 在anaconda shell控制台中,切换至虚拟环境, 安装TensorFlow 这是用…...

【Leetcode热题】打卡 day11——20(更新至11)
1、合并两个有序链表 - 链表 暴力 / 递归 21. 合并两个有序链表 (1)暴力 class Solution {public ListNode mergeTwoLists(ListNode l1, ListNode l2) {ListNode dummynew ListNode();ListNode curdummy;while(l1!null&&l2!null){if(l1.val&l…...

linux使用操作[3]
文章目录 版权声明环境变量$符号自行设置环境变量 上传、下载rz、sz命令 压缩、解压tar命令压缩tar解压zip 命令压缩文件unzip 命令解压文件 版权声明 本博客的内容基于我个人学习黑马程序员课程的学习笔记整理而成。我特此声明,所有版权属于黑马程序员或相关权利人…...

梦想让生活得以忍受-寄语机器视觉工程师
我,曾梦想梦想走天涯,看看这世界的繁华,年少的心总有些轻狂,如今四海为家。 大家都听过这首歌,迎来很多打工人的共鸣,著名作家海明威曾说,“一个人可以被打败,但不可以被毁灭”&…...
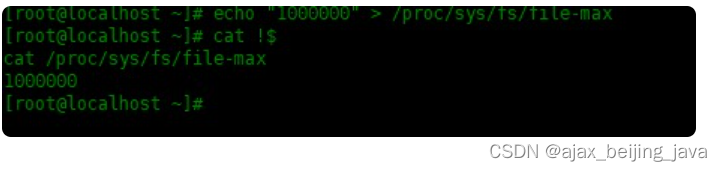
linux 设置打开文件数
可以使用下面的文件进行设置 /etc/security/limits.d/90-nproc.conf 先来看/etc/security/limits.d/90-nproc.conf 配置文件: [root ~]# cat /etc/security/limits.d/90-nproc.conf # Default limit for number of users processes to prevent # accidental fork…...

MySQL基础篇-约束
目录 1.约束概述 2.分类 3.测试user表的约束情况 主键约束 非空约束及唯一约束 检查约束 默认约束 4.外键约束 外键约束的语法 外键约束的删除/更新行为 小结 1.约束概述 MySQL约束(Constraints)是用于确保表中数据完整性和一致性的规则。它们定…...

系统工程知识体系(SEBoK)
介绍 《系统工程知识体系》(SEBoK)是以一种理念设计的,即如果工程师有一个实时更新、实用的指南,他们就能做出更优秀的工作。如果你以前没有使用过这个资源,也没有关系;因为已经有一个完整的指南供你参考&…...
)
Spring DI (Dependency Injection)
What Is DI? 当一个类需要依赖另一个对象,把另一个对象实例化之后注入给这个对象的过程我们称之为DI # Create an object dependency in traditional programming public class Store {private Item item;public Store() {item new ItemImpl1(); } }# Using …...
Spring Boot : ORM 框架 JPA 与连接池 Hikari
数据库方面我们选用 Mysql , Spring Boot 提供了直接使用 JDBC 的方式连接数据库,毕竟使用 JDBC 并不是很方便,需要我们自己写更多的代码才能使用,一般而言在 Spring Boot 中我们常用的 ORM 框架有 JPA 和 Mybaties ,本…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
