关于坐标的旋转变换和坐标系的旋转变换
不管是坐标的旋转变换还是坐标系下的旋转变换,只和旋转的顺时针和逆时针有关。然坐标系间的顺时针和逆时针是根据当前坐标系在目标坐标系下的相对位置确定。
一。逆时针旋转belta角度的公式

二。顺时针旋转belta角度的公式

三。坐标的旋转变换
1.坐标的旋转变换相对简单,逆时针旋转theta
如下图, 在2维坐标上,有一点p(x, y) , 直线op的长度为r, 直线op和x轴的正向的夹角为a。 直线op围绕原点做逆时针方向b度的旋转,到达p’ (s,t)

二。坐标系的旋转变换
1.建立坐标系,坐标系可以是左手坐标系,或者右手坐标系.
2.根据建立的坐标系,得到当前坐标系在目标坐标系下的旋转角度,如下,xoy坐标系在sot坐标系下的-theta角度方向,xoy需要逆时针转theta到sot。
3.假定现在是右手坐标系,当前坐标系转到目标坐标系是逆时针旋转theta,那么当前坐标系下的坐标转换到目标坐标系下的坐标就是逆时针旋转-theta,等于顺时针旋转theta。
4.例如在原坐标系xoy中, 绕原点沿逆时针方向旋转theta度, 变成座标系 sot。
设有某点p,在原坐标系中的坐标为 (x, y), 旋转后的新坐标为(s, t)。如下

5.例如左手坐标系下
原坐标系xoy中, 绕原点沿逆时针方向旋转theta度, 变成座标系 sot。
设有某点p,在原坐标系中的坐标为 (x, y), 旋转后的新坐标为(s, t)。如下,在sot坐标系下的-theta角度是xoy,即顺时针方向theta角度,xoy坐标系转到sot坐标系需要逆时针旋转theta,所以xoy坐标系下的坐标转到sot坐标系下的坐标需要逆时针旋转-theta,等于顺时针旋转theta,公式入下。

总结,坐标或者坐标系的旋转变换和建立的坐标系是左手还是右手没有关系,只和旋转的方向有关。假如我们只知道坐标系之间的角度关系,可通过建立的坐标系类型确定顺时针还是逆时针。
参考文章 :
二维坐标系旋转矩阵的求解(坐标系不变和坐标系改变两种情况)_二维坐标旋转矩阵-CSDN博客
旋转变换(一)旋转矩阵-CSDN博客
相关文章:

关于坐标的旋转变换和坐标系的旋转变换
不管是坐标的旋转变换还是坐标系下的旋转变换,只和旋转的顺时针和逆时针有关。然坐标系间的顺时针和逆时针是根据当前坐标系在目标坐标系下的相对位置确定。 一。逆时针旋转belta角度的公式 二。顺时针旋转belta角度的公式 三。坐标的旋转变换 1.坐标的旋转变换相…...
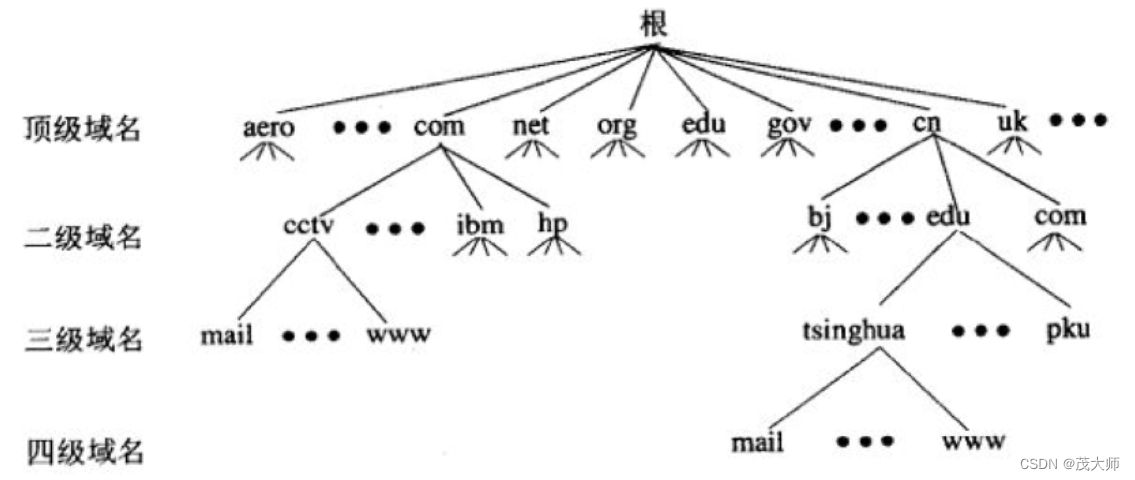
2023.9.19 关于 数据链路层 和 DNS 协议 基本知识
目录 数据链路层 MTU DNS 协议 补充 DHCP协议 数据链路层 基本概念: 考虑相邻两个节点之间的传输(通过 网线 / 光纤 / 无线 直接相连的两个设备)以太网协议 规定了 数据链路层 和 物理层 的内容 IP地址 与 mac地址 的相互配合 IP地址 描…...

如何保证接口幂等性
简介 接口幂等性就是说用户使用相同的参数请求同一个接口无论是一次还是多次都应该是一样的。不会因为多次的点击产生不同效果。 举个栗子:一个用户在手机APP上提200块钱,然后一不小心点击了两次,那么就应该只提取出200块钱,不应…...
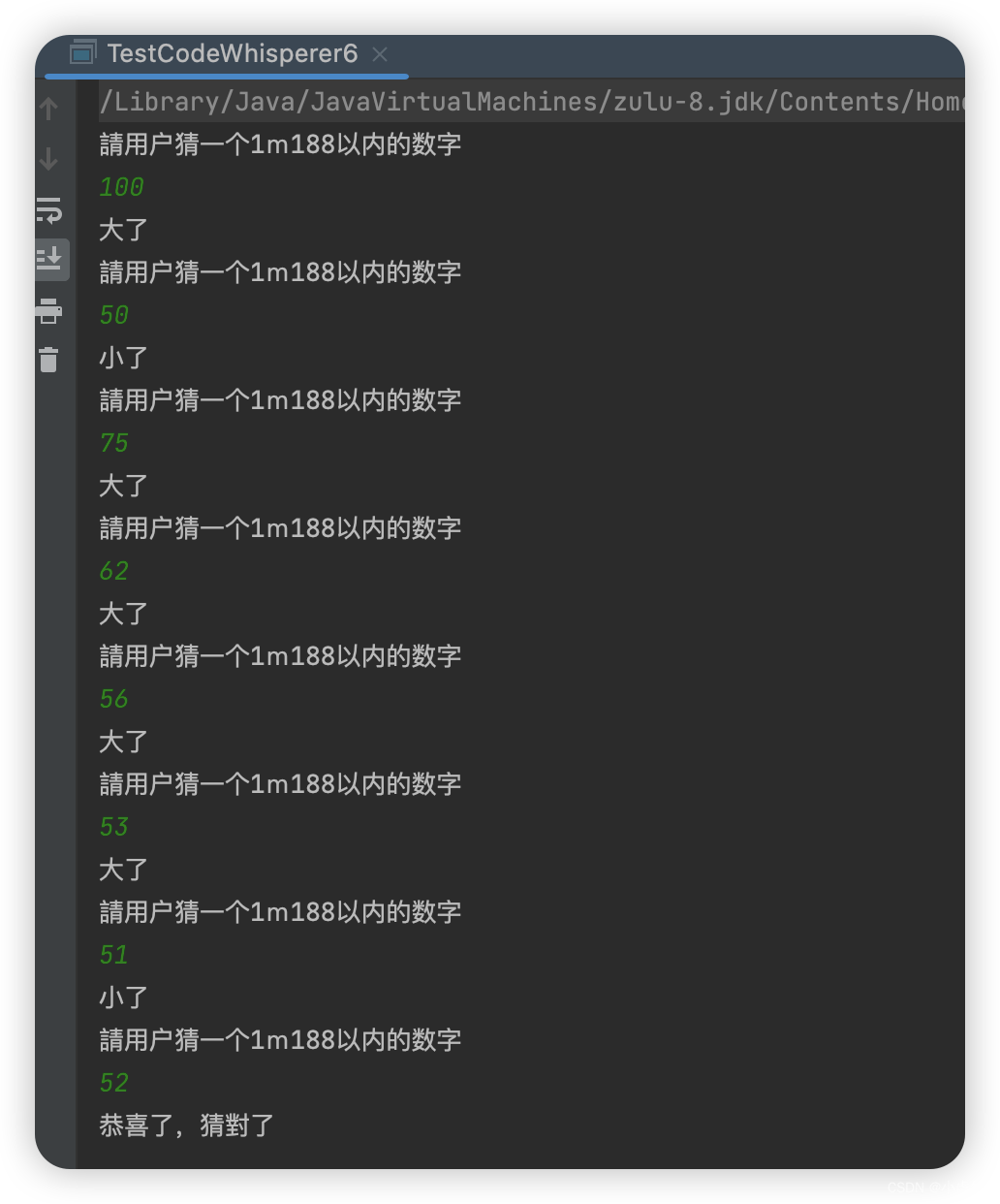
搭建智能桥梁,Amazon CodeWhisperer助您轻松编程
零:前言 随着时间的推移,人工智能技术以惊人的速度向前发展,正掀起着全新的编程范式革命。不仅仅局限于代码生成,智能编程助手等创新应用也进一步提升了开发效率和代码质量,极大地推动着软件开发领域的快速繁荣。 当前…...
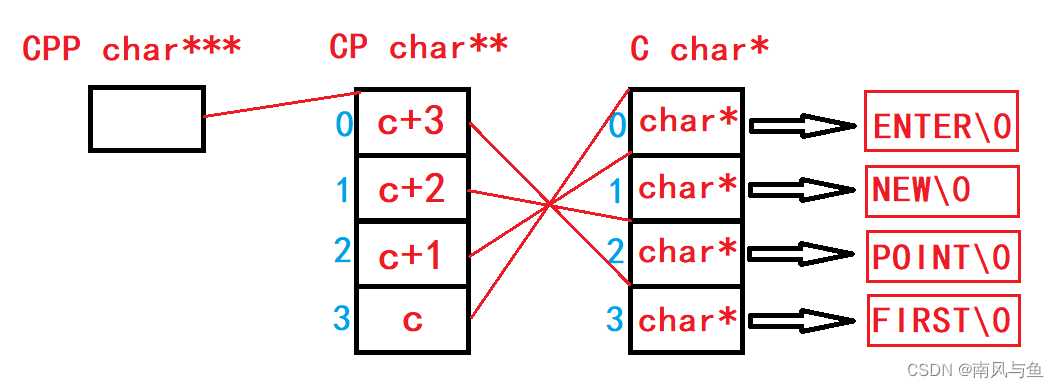
数组和指针笔试题解析之【指针】
目录 🍂笔试题1: 🍂笔试题2: 🍂笔试题3: 🍂笔试题4: 🍂笔试题5: 🍂笔试题6: 🍂笔试题7: 🍂笔试题…...
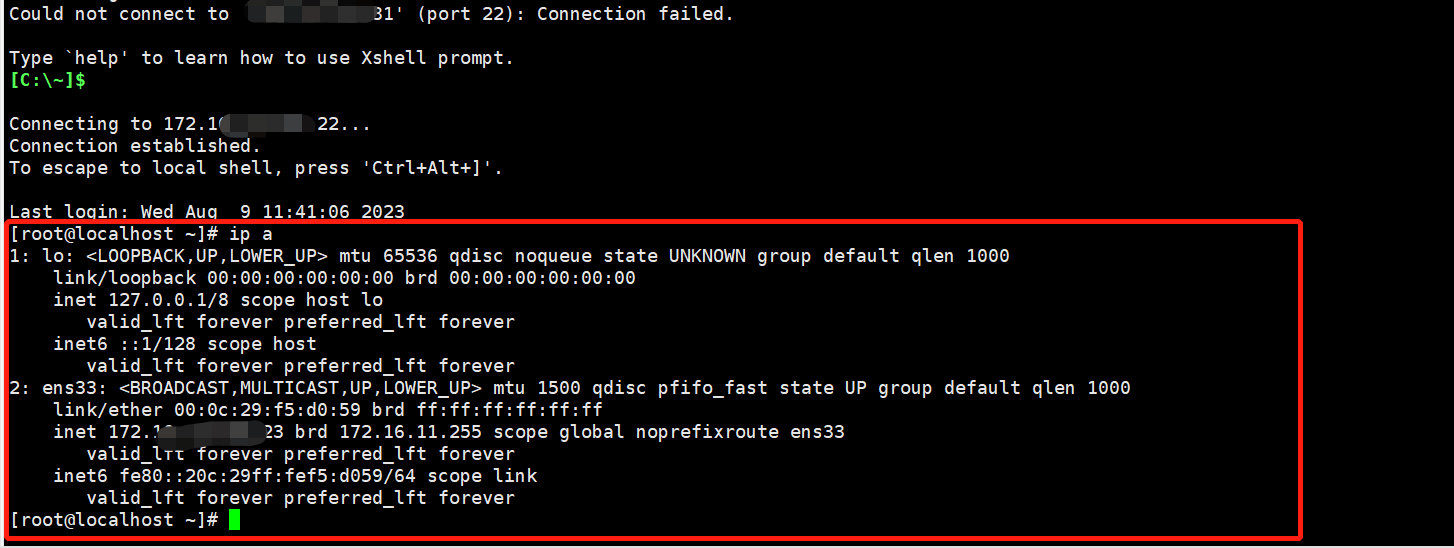
【Linux】之Centos7卸载KVM虚拟化服务
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...
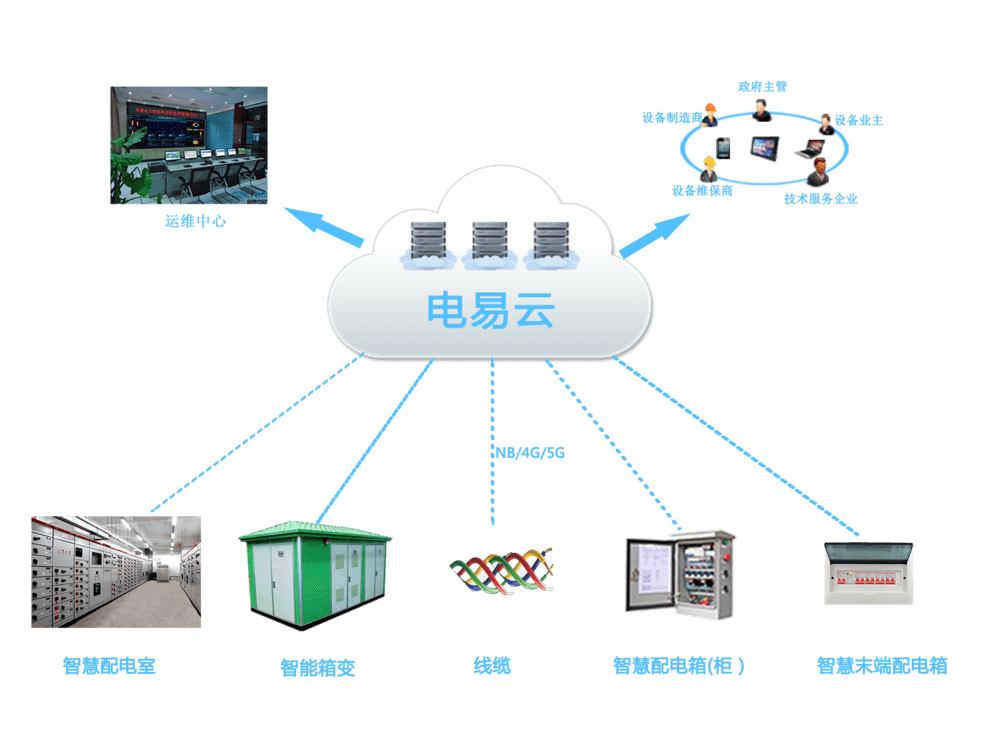
智能电力运维系统:数字化转型在电力行业的关键应用
随着信息技术、人工智能等的飞速发展,数字化改造已成为各行各业的重要发展趋势。在电力行业中,智能电力运维系统是数字化转型的关键应用之一。 力安科技智能电力运维系统是一种集自动化、智能化、云计算、物联网等先进技术于一体的电力运维管理解决方…...

eslint报错:no-empty-source
问题: 提交代码时,eslint校验没有通过,报错 esc[2m183:9esc[22m esc[31mesc[31m✖esc[39m Unexpected empty source esc[2mno-empty-sourceesc[22m 1 problem (esc[31m1 erroresc[39m, esc[33m0 warnings esc[39m) 原因: …...
)
图论17(Leetcode864.获取所有钥匙的最短路径)
用二进制表示获得的钥匙,假设n钥匙个数 000000000代表没有钥匙,0000000001代表有idx为1的钥匙,0000000011代表有idx1,2的钥匙 (这方法巧妙又复杂.. 代码: class Solution {static int[][] dirs {{-1,0}…...
vue 脚手架 入门 记录
vue 脚手架 入门 记录 以管理员身份运行PowerShell执行:get-ExecutionPolicy,回复Restricted,表示状态是禁止的 3.执行:set-ExecutionPolicy RemoteSigned 4.选择Y 注意:一定要以管理员的身份运行PowerShellÿ…...

汽车租赁系统演示租车小程序H5开发
一款适合汽车租赁业务的程序系统,支持在线支付、一键续租、在线签名。 为了方便用户端方便租车和查看已租车辆的信息和费用,支持上门取车和到店取车两种模式,支持待付款、待取车、待还车、订单管理、已完成、全部订单等订单状态查看和处理功…...

【MySQL】 MySQL 更新数据机制
MySQL 更新数据机制 一、问题描述 假设我们有这样一张表,且包含一条记录: CREATE TABLE mytest ( id int(11) NOT NULL, c1 int(11) DEFAULT NULL, c2 int(11) DEFAULT NULL, c3 int(11) DEFAULT NULL, PRIMARY KEY (id), KEY c1 (c1), KEY c2 (c2) 包…...

批次管理在MES管理系统中有哪些应用
在制造企业中,批次管理是一项至关重要的管理方法,它贯穿于企业的整个生产过程中。特别是在流程制造行业中,如药品、食品等行业,批次管理显得尤为重要。这些行业的产品通常需要进行严格的质量控制和追踪,以便在问题发生…...

python命名规范
一、概述 以前写python代码没有个代码,写出的代码一点也不规范 二、命名规范 2.1类的命名规范 总是使用首字母大写单词串。如MyClass、ClassName。内部类可以使用额外的前导下划线。 2.2函数和方法的命名规范 小写下划线,如method_name。 2.3函数…...

Redis学习笔记--002
Redis的JAVA客户端 文章目录 Redis的JAVA客户端一、Redis的Java客户端的种类二、Jedis2.1、使用步骤2.2、Jedis连接池 三、[SpringDataRedis](https://spring.io/projects/spring-data-redis)3.1、介绍3.2、RedisTemplate3.3、SpringDataRedis使用步骤3.4、SpringDataRedis的序…...

Visual Stdio 2019 win10 64bit下 无法找到 资源编译器DLL,请确认路径是否正确,和无法下载 win10SDK_10.0
上面的2个原因 第一个原因是因为安装时候,漏掉勾选 vistual stdio sdk 和 windows 通用c运行时 其中的一项目 第2个原因是没有安装 sdk...
)
设计模式:中介者模式(C++实现)
在中介者模式中,中介者对象负责协调多个对象之间的交互,将对象之间的耦合度降低。 #include <iostream> #include <string> #include <vector>class Colleague;// 中介者接口 class Mediator { public:virtual void sendMessage(Coll…...

Python常用函数
最近跑实验,记录一些常用的 Python 函数,便于自己复习和学习,仅用来学习。 1.Python 中的 os.path.join() 参考该文章 深度了解 在 Python 中,处理文件和目录路径是常见的任务。为了简化路径的拼接和操作,Python 提供…...
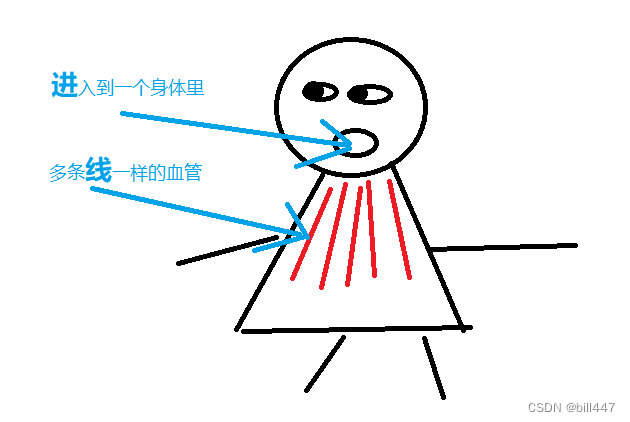
进程与线程的记忆方法
有很多人经常会分不清进程与线程的关系, 嗯。。。。。。可能只有我自己记不清吧 举个例子: 进程:登录一个qq号,就是一个进程。 线程:同时打开多个窗口聊天,就是多个线程。 每次记忆完,过了一段…...

支持私有化部署的 WorkPlus,助您构建定制化的即时通讯平台
随着信息技术的飞速发展,企业对于即时通讯平台的需求也不断提升。而在信息安全日益重要的时代背景下,随之而来的是对数据保护和隐私安全的高度关注。私有化即时通讯平台应运而生,成为企业保护数据安全的守护者。在众多品牌中,Work…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
