面试算法13:二维子矩阵的数字之和
题目
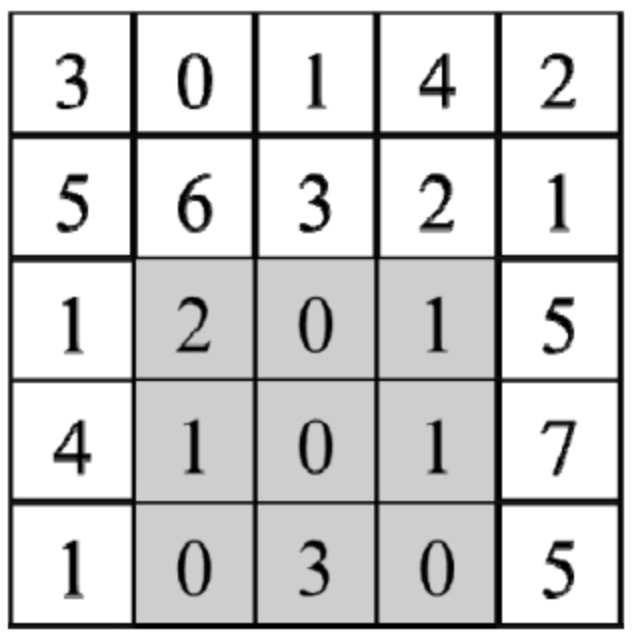
输入一个二维矩阵,如何计算给定左上角坐标和右下角坐标的子矩阵的数字之和?对于同一个二维矩阵,计算子矩阵的数字之和的函数可能由于输入不同的坐标而被反复调用多次。例如,输入图2.1中的二维矩阵,以及左上角坐标为(2,1)和右下角坐标为(4,3)的子矩阵,该函数输出8。
分析
如果不考虑时间复杂度,则采用蛮力法用两个嵌套的循环总是可以求出一个二维矩阵的数字之和。如果矩阵的行数和列数分别是m和n,那么这种蛮力法的时间复杂度是O(mn)。
只是这个题目提到,对于一个二维矩阵,可能由于输入不同的坐标而反复求不同子矩阵的数字之和,这说明应该优化求和的过程,要尽可能快地实现子矩阵的数字求和。
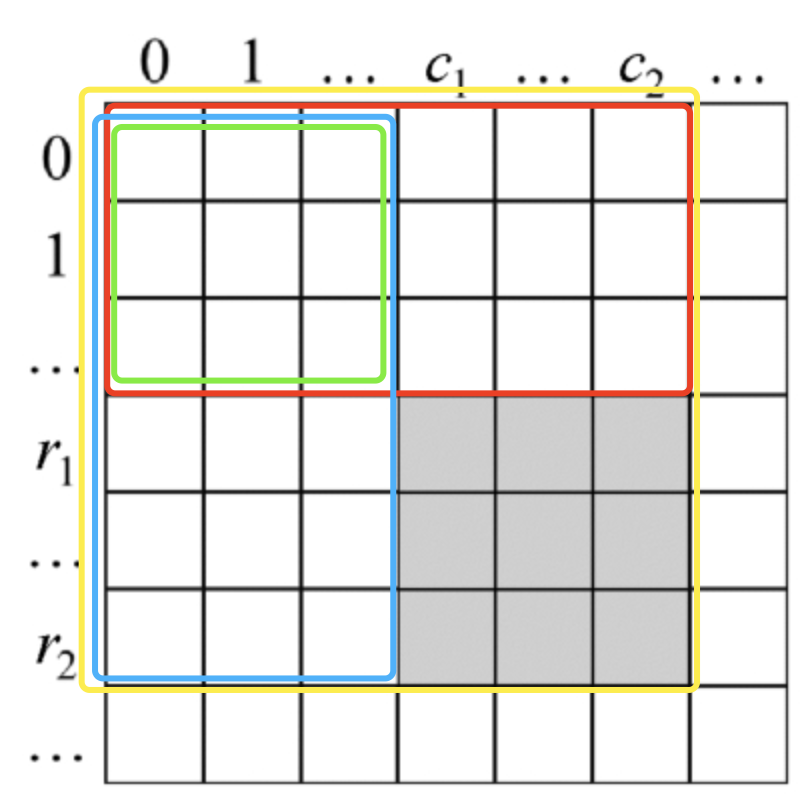
阴影面积 = 黄色正方形面积 + 绿色正方行面积 - 红色长方形面积 - 蓝色长方形面积
因此,可以在预处理阶段求出从左上角坐标为(0,0)到每个右下角坐标的子矩阵的数字之和。首先创建一个和输入矩阵大小相同的辅助矩阵sums,该矩阵中的坐标(i,j)的数值为输入矩阵中从左上角坐标(0,0)到右下角坐标(i,j)的子矩阵的数字之和。
下面分析如何生成辅助矩阵sums,即求得数组中的每个数字sums[i][j]。按照生成辅助矩阵sums的规则,sums[i][j]的值等于输入矩阵中从左上角坐标为(0,0)到右下角坐标为(i,j)的子矩阵的数字之和。可以把从左上角坐标为(0,0)到右下角坐标为(i,j)的子矩阵的数字看成由两部分组成。第1部分是从左上角坐标为(0,0)到右下角坐标为(i-1,j)的子矩阵,该子矩阵的数字之和等于sums[i-1][j]。第2部分是输入矩阵中第i行中列号从0到j的所有数字。如果按照从左到右的顺序计算sums[i][j],则可以逐个累加第i行的数字,从而得到子矩阵第2部分的数字之和。
解
public class Test {public static void main(String[] args) {int[][] nums = {{3, 0, 1, 4, 2},{5, 6, 3, 2, 1},{1, 2, 0, 1, 5},{4, 1, 0, 1, 7},{1, 0, 3, 0, 5}};sums = generateNumMatrix(nums);int result = sumRegion(2, 1, 4, 3);System.out.println(result);}private static int[][] sums;public static int[][] generateNumMatrix(int[][] matrix) {if (matrix.length == 0 || matrix[0].length == 0) {return null;}int[][] sums = new int[matrix.length + 1][matrix[0].length + 1];for (int i = 0; i < matrix.length; i++) {int rowSum = 0;for (int j = 0; j < matrix[0].length; j++) {rowSum += matrix[i][j];sums[i + 1][j + 1] = sums[i][j + 1] + rowSum;}}return sums;}public static int sumRegion(int row1, int col1, int row2, int col2) {//return sums[row2][col2] + sums[row1-1][col1-1] - sums[row1-1][col2] - sums[row2][col1-1];return sums[row2 + 1][col2 + 1] + sums[row1][col1] - sums[row1][col2 + 1] - sums[row2 + 1][col1];}
}
如果输入矩阵的行数和列数分别是m和n,那么辅助数组sums的行数和列数分别为m+1和n+1,这样只是为了简化代码逻辑。如果用公式sums[r2][c2]+sums[r1-1][c2]-sums[r2][c1-1]+sums[r1-1][c1-1]求解左上角坐标为(r1,c1)、右下角坐标为(r2,c2)的子矩阵的数字之和,由于坐标值r1或c1有可能等于0,因此r1-1或c1-1可能是负数,不再是有效的数组下标。如果在矩阵的最上面增加一行,最左面增加一列,这样就不必担心出现数组下标为-1的情形。
相关文章:

面试算法13:二维子矩阵的数字之和
题目 输入一个二维矩阵,如何计算给定左上角坐标和右下角坐标的子矩阵的数字之和?对于同一个二维矩阵,计算子矩阵的数字之和的函数可能由于输入不同的坐标而被反复调用多次。例如,输入图2.1中的二维矩阵,以及左上角坐标…...

Vue安装插件时候中遇到冲突依赖解决方案
错误如下: npm ERR! code ERESOLVE npm ERR! ERESOLVE could not resolve npm ERR! npm ERR! While resolving: vue/eslint-config-standard6.1.0 npm ERR! Found: eslint-plugin-vue8.7.1 npm ERR! node_modules/eslint-plugin-vue npm ERR! dev eslint-pl…...
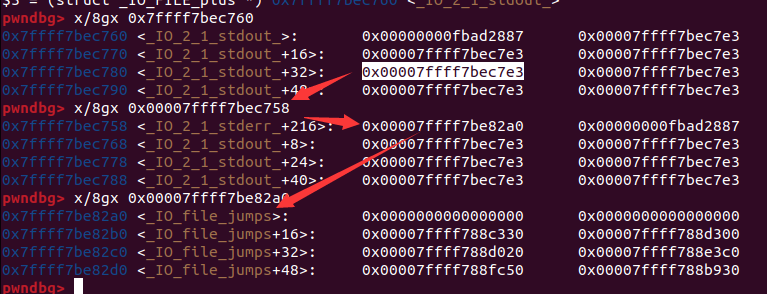
realloc函数应用IO泄露体验
本题主要介绍realloc函数,平时我们使用realloc最多便是在打malloc_hook–>onegadget的时候,使用realloc_hook调整onegadget的栈帧,从而getshell。 在realloc函数中,也能像malloc一样创建堆,并且比malloc麻烦一些&a…...
野指针)
(c语言)野指针
#include<stdio.h> //野指针 int* test() { int a 10; return &a; } int main() { //野指针一: int* p; *p 10; //非法访问内存 //p没有初始化,就意味着没有明确的指向 //一个局部变量不初始化的话ÿ…...

【Git】轻松学会 Git(一):掌握 Git 的基本操作
文章目录 前言一、创建 Git 本地仓库1.1 什么是仓库1.2 创建本地仓库1.3 .git 目录结构 二、配置 Git三、认识 Git 的工作区、暂存区和版本库3.1 什么是 Git 的工作区、暂存区和版本库3.2 工作区、暂存区和版本库之间的关系 四、添加文件4.1 添加文件到暂存区和版本库中的命令4…...

rust trait对象
在拥有继承的语言中,可以定义一个名为shape的基类,该类上有一个draw方法。其他的类比如Button、SelectBox继承shape。它们各自覆盖draw方法。调用这些子类的draw方法时,就可以把它们统一当作shape来使用。不过Rust并没有继承,如果…...
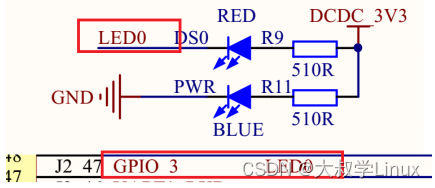
Linux学习第21天:Linux内核定时器驱动开发: 流淌的时间长河
Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 在人类的发展进化中,时间是一个非常重要神秘的物质量。任何事物都是在时间的长河中流淌发生、发展、变化。我们进行驱动开发中对时间的定义和使用也是…...

Centos服务在服务器重启后自启
以Dolphin为例 打开rc.local文件以编辑: sudo vi /etc/rc.d/rc.local在文件中添加您的启动命令。在您的情况下,要添加的命令如下: sh /opt/dolphinscheduler/zookeeper/bin/zkServer.sh start sh /opt/dolphinscheduler/dolphinscheduler/…...
慢性疼痛治疗服务公司Kindly MD申请700万美元纳斯达克IPO上市
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,慢性疼痛治疗服务公司Kindly MD近期已向美国证券交易委员会(SEC)提交招股书,申请在纳斯达克IPO上市,股票代码为(KDLY),Kindly MD计划通过…...
代码随想录 Day6 哈希 LeetcodeT454 四数之和II T383赎金信 T15 三数之和 T18 四数之和
本文代码思路来源于: 代码随想录 前言 希望大家在刷这部分题的时候先熟悉熟悉哈希结构的基本常用api,比较方便理解. LeetCode T454 四数之和 题目链接:454. 四数相加 II - 力扣(LeetCode) 题目思路 暴力解法仍然是遍历四个数组解决此题, 哈希的思路有…...

干货速来|教你如何撰写毕业论文
撰写毕业论文对于正常大学毕业至关重要。毕业论文是对学生在大学期间所学知识的综合运用和深入研究的体现,也是对学术能力和独立思考能力的考验。 撰写毕业论文的过程需要学生投入大量的时间和精力,包括选题、文献综述、研究方法选择、数据收集和分析、…...

【ROS 2】-2 话题通信
飞书原文链接: Docs...

Unity之NetCode多人网络游戏联机对战教程(2)--简单实现联机
文章目录 1.添加基本组件2.创建NetworkManager组件3.创建Player4.创建地面5.创建GameManager6.编译运行7. 测试联机后话 1.添加基本组件 NetworkManagerPlayerScene 2.创建NetworkManager组件 创建一个空物体,命名为NetworkManager 选择刚刚创建的NetworkManager…...
makdown文法
这里写自定义目录标题 欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题,有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants 创建一个自定义列表如何创建一个…...

新手程序员怎么接单?
程序员如何在自己年富力强的时候,最大化发挥自己的能力?将超能力转化为“钞能力”? 有人还在苦哈哈当老黄牛,一身使不完的牛劲,有人已经另辟蹊径,开创了自己的一片致富小天地。 接单找兼职,就…...
接口测试——接口协议抓包分析与mock_L2
目录: 抓包工具charles抓包工具fiddler抓包工具证书配置app抓包实战练习接口测试实战练习 1.抓包工具charles 工具介绍 支持 SSL 代理支持流量控制支持重发网络请求,方便后端调试支持修改网络请求参数支持网络请求的截获并动态修改可以自动将 json 或…...
Seata入门系列【1】安装seata 1.7.1+nacos 2.1.1
1 介绍 Seata 是一款开源的分布式事务解决方案,致力于提供高性能和简单易用的分布式事务服务。Seata 将为用户提供了 AT、TCC、SAGA 和 XA 事务模式,为用户打造一站式的分布式解决方案。 Github: https://github.com/seata/seata 官方文档:h…...
2023年职业院校技能大赛中职组----大数据应用与服务赛项任务书试题
2023年职业院校技能大赛中职组----大数据应用与服务赛项任务书试题 模块一:数据库系统运维(25分)任务一:数据库系统搭建(10分)任务二:房源数据库系统运维(15分) 模块二&a…...

产品经理的职业前景怎么样?一文为你全面解答!
随着科技的迅速发展和市场竞争的日益激烈,产品经理这个职业变得越来越炙手可热。产品经理负责一款产品的全生命周期管理,从需求收集到设计、开发、测试、发布,再到市场推广和用户反馈,都需要产品经理参与决策。因此,这…...

【深度学习】图像去噪(2)——常见网络学习
【深度学习】图像去噪 是在 【深度学习】计算机视觉 系列文章的基础上,再次针对深度学习(尤其是图像去噪方面)的基础知识有更深入学习和巩固。 1 DnCNN 1.1 网络结构 1.1.1 残差学习 1.1.2 Batch Normalization (BN) 1.1.2.1 背景和目标…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
