基于遗传算法解决的多仓库多旅行推销员问题（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

我们提出了一个使用遗传算法（GA）解决多仓库的改进型旅行商问题（MTSP）的解决方案。在这个问题中，我们考虑了具有可变数量的销售人员的情况。

我们的算法以找到（近乎）最佳解决方案为目标，该解决方案能满足一些约束条件，如每个城市只被访问一次，每个销售人员从一个仓库开始并结束行程等。

我们的算法是基于约瑟夫·柯克（Joseph Kirk）的MTSPV_GA算法，但我们进行了一些改进。首先，每个销售人员都有一个特定的起始和结束仓库，以确保他们的路线是闭合的。其次，我们引入了两个可能的成本函数，允许我们寻找最小总和的游览长度（与原始版本相似），或者找到最短的游览长度。后者有时被称为MinMaxMDMTSP。

总体而言，我们的算法的关键特点如下：
1. 每个销售人员从一个仓库开始，按照特定的路线访问一组唯一的城市，最后返回起始仓库。
2. 每个城市仅由一个销售人员访问，确保每个城市只被访问一次。

通过使用这个改进的遗传算法解决方案，我们可以找到多仓库MTSP问题的最佳或接近最佳的解决方案。这将有助于优化商业配送、旅行路线规划等各种现实应用场景，并提高效率和效益。我们的研究为该领域的进一步探索和改进提供了有价值的基础。

📚2 运行结果

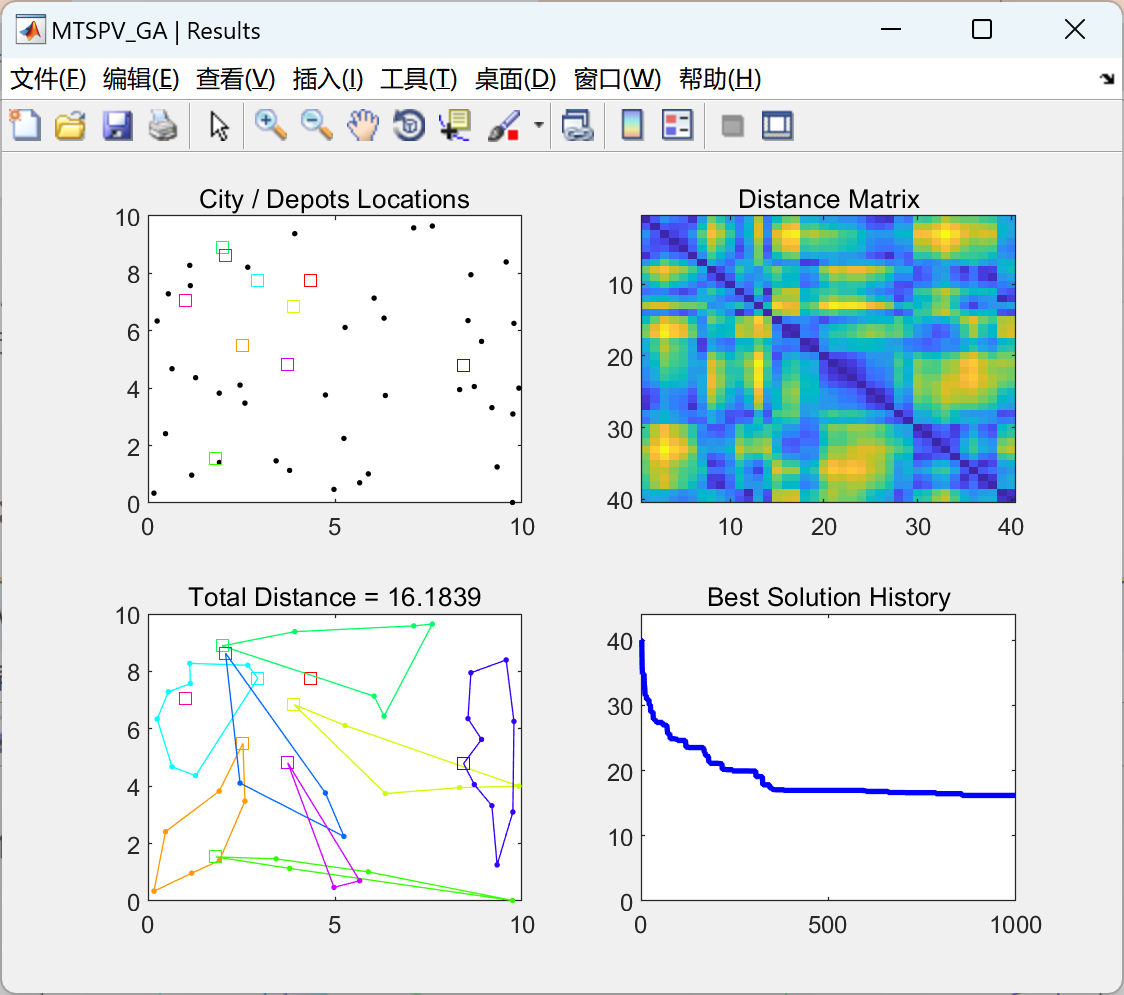
部分代码：

% Run the GA
global_min = Inf;
total_dist = zeros(1,pop_size);
dist_history = zeros(1,num_iter);
tmp_pop_rte = zeros(8,n);
tmp_pop_brk = cell(8,1);
new_pop_rte = zeros(pop_size,n);
new_pop_brk = cell(pop_size,1);
if show_progpfig = figure('Name','MTSPV_GA | Current Best Solution','Numbertitle','off');
end
iter=0;
iter2go=0;
while iter2go < num_iteriter2go=iter2go+1;iter=iter+1;% Evaluate Each Population Member (Calculate Total Distance)for p = 1:pop_sized = [];p_rte = pop_rte(p,:);p_brk = pop_brk{p};salesmen = length(p_brk)+1;rng=CalcRange(p_brk,n);

% Run the GA
global_min = Inf;
total_dist = zeros(1,pop_size);
dist_history = zeros(1,num_iter);
tmp_pop_rte = zeros(8,n);
tmp_pop_brk = cell(8,1);
new_pop_rte = zeros(pop_size,n);
new_pop_brk = cell(pop_size,1);
if show_prog
    pfig = figure('Name','MTSPV_GA | Current Best Solution','Numbertitle','off');
end
iter=0;
iter2go=0;
while iter2go < num_iter
    iter2go=iter2go+1;
    iter=iter+1;
    % Evaluate Each Population Member (Calculate Total Distance)
    for p = 1:pop_size
        d = [];
        p_rte = pop_rte(p,:);
        p_brk = pop_brk{p};
        salesmen = length(p_brk)+1;
        rng=CalcRange(p_brk,n); 

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]赵赫,杜端甫.遗传算法求解旅行推销员问题时算子的设计与选择[J].系统工程理论与实践, 1998(02):62-65.DOI:10.3321/j.issn:1000-6788.1998.02.012.

[2]吴云,姜麟,刘强.基于并行遗传算法多旅行商问题的求解[J].微型电脑应用, 2011(7):4.DOI:10.3969/j.issn.1007-757X.2011.07.015.

[3]孙文彬,王江.一种基于遗传算法的TSP问题多策略优化求解方法[J].地理与地理信息科学, 2016, 32(4):4.DOI:10.3969/j.issn.1672-0504.2016.04.001.

🌈4 Matlab代码实现