《计算机视觉中的多视图几何》笔记(7)
7 Computation of the Camera Matrix P P P
这章讲的是摄像机参数估计。摄像机标定,本质上就是求摄像机矩阵 P P P,当我们知道足够多的 X ↔ x X \leftrightarrow x X↔x,我们该如何计算 P P P?如果知道3D和2D点的对应,那么内参和外参可以由基本的线性方程求解问题算出。遇到超定解时的解决办法也跟前面讲的第4章射影变换的情况非常类似。值得注意的是,第4章求的是 3 × 3 3 \times 3 3×3射影变换矩阵,而本章求的是 3 × 4 3 \times 4 3×4相机矩阵。
文章目录
- 7 Computation of the Camera Matrix P P P
- 7.1 Basic equations
- 7.2 Geometric error
- 7.2.1 Geometric interpretation of algebraic error
- 7.2.2 Estimation of an affine camera
- 7.3 Restricted camera estimation
- 7.4 Radial distortion
7.1 Basic equations
问题描述:我们假设有一些3D空间上的点 X i X_{i} Xi和2D图像上的点 x i x_{i} xi的对应关系已经给出。我们的目标是找到一个 3 × 4 3 \times 4 3×4的摄像机矩阵 P P P,满足对于所有 i i i都满足 x i = P X i x_{i}=PX_{i} xi=PXi。
我们可以发现,这个问题和在第4章里面说的求解2D射影变换矩阵 H H H非常像,唯一的区别是需要求解的矩阵维度变了而已。
最基本的方法就是方程 P X = x PX=x PX=x,然后变成 x × P X = 0 x \times PX = 0 x×PX=0 取该矩阵前两行,因为第三行是线性相关的。这样,我们可以写成 A p = 0 Ap=0 Ap=0,这 A A A就是一个 2 n × 12 2n \times 12 2n×12的矩阵。我们要求解摄像机矩阵,其实也就是要求解这个等式里面的 p p p。
最小解 因为 P P P是 3 × 4 = 12 3 \times 4 = 12 3×4=12个元素,那么就有11个自由度,理论上我们需要5.5对对应点就行,0.5对对应点就是知道x或者y坐标就可以了。
超定的情况 如果我们有多于6对点,那我们就求 m i n ∣ ∣ A p ∣ ∣ = 0 min||Ap||=0 min∣∣Ap∣∣=0,并且让他满足约束 ∣ ∣ p ∣ ∣ = 1 ||p||=1 ∣∣p∣∣=1, ∣ ∣ p ^ 3 ∣ ∣ ||\hat{p}^3|| ∣∣p^3∣∣=1, p ^ 3 \hat{p}^3 p^3就是p最后一行的前三个元素。
退化的情况 有两种情况可以使我们不能唯一确定 p p p:
- 相机和点都在一个扭曲的立方体上
- 相机和点都在平面上,且该平面一直线通过相机的中心
对于这样的配置,不能从点的图像中唯一地获得相机。 相反,它可以分别沿着扭曲的立方体或直线任意移动。 如果数据接近退化的情况,则获得的 P P P估计值很差。 例如,如果相机距离场景较远,例如鸟瞰图,则这种情况接近平面退化。
点的归一化 我们需要把所有点到直线的平均距离归一化到 3 \sqrt{3} 3。
从线对应来计算 P P P 如果我们能找到一对对应线,那么我们就有方程 l T P X j = 0 l^TPX_j=0 lTPXj=0其中 j = 0 , 1 j=0,1 j=0,1, X X X在 l l l上。
7.2 Geometric error
回忆我们在第4章提到的几何损失函数,我们可以把它用在这里:
min P ∑ i d ( x , P X ) 2 \min_P \sum_{i} d(x,PX)^2 Pmini∑d(x,PX)2

世界坐标系里的误差 我们考虑世界坐标系,也就是标定板上的误差。因为 P X PX PX不可能完全等于 x x x。反过来, x x x对应的世界坐标系里的点,也不会完全是 X X X,那么我们就假设 x x x对应的世界坐标系里的点是 X ^ \hat{X} X^,然后我们同时考虑世界坐标系的误差,和图像上的误差
∑ i = 1 n d M a h ( x i , P X i ^ ) 2 + d M a h ( X i , X i ^ ) 2 \sum_{i=1}^{n} d_{Mah}(x_{i}, P \hat{X_{i}})^2 + d_{Mah}(X_{i}, \hat{X_{i}})^2 i=1∑ndMah(xi,PXi^)2+dMah(Xi,Xi^)2
也就是说在图像上 x i x_{i} xi要靠近 P X i ^ P \hat{X_{i}} PXi^,在世界坐标系里 X i X_{i} Xi也要靠近 P X i ^ P \hat{X_{i}} PXi^。
7.2.1 Geometric interpretation of algebraic error
代数误差的几何解释:代数误差找一个点 X ′ X' X′尽可能的接近 X X X。
7.2.2 Estimation of an affine camera
上述所有方法都可以直接用在仿射摄像机上。
7.3 Restricted camera estimation
通常我们会对 P P P矩阵做出一些限制:
- 偏斜系数 s s s是0
- 像素是正方形,即 a x = a y a_{x}=a_{y} ax=ay
- 主点 ( x 0 , y 0 ) (x_{0},y_{0}) (x0,y0)已知
- K K K已知
这几点假设不是同时成立的。比如我们可以只用1和2,那么 P P P矩阵就只剩下3+6=9个系数了。
迭代方法的初始化 如果我们求几何损失函数,要用迭代的方法。那么迭代的初值从哪里来? 可以用DLT先解出一个值作为初始值。
7.4 Radial distortion
相机畸变主要是径向畸变,所谓径向就是圆的直径的方向。该畸变会使正方形变得接近于一个圆,所以叫径向畸变。
校正的思想很简单。所谓畸变,就是给像素坐标 ( x , y ) (x,y) (x,y)乘上一个函数 L ( r ) L(r) L(r),我们只需要用泰勒展开去近似这个函数就好了,剩下的工作就是确定泰勒展开的系数。这个展开的系数作为内参,把它们一起标定出来就可以了。
相关文章:

《计算机视觉中的多视图几何》笔记(7)
7 Computation of the Camera Matrix P P P 这章讲的是摄像机参数估计。摄像机标定,本质上就是求摄像机矩阵 P P P,当我们知道足够多的 X ↔ x X \leftrightarrow x X↔x,我们该如何计算 P P P?如果知道3D和2D点的对应ÿ…...

Python经典练习题(四)
文章目录 🍀第一题🍀第二题🍀第三题 🍀第一题 题目:打印出如下图案(菱形): 我们首先分析一下,本题实现的步骤主要有两个,分别是前四行和后三行 前四行:第一…...

Mac Pro在重装系统时提示“未能与恢复服务器取得联系”
检查网络连接: 确保你的Mac Pro连接到稳定的网络。尝试更换其他网络,例如切换到不同的Wi-Fi或使用有线连接。 系统时间校正: 错误的系统时间有时会导致与恢复服务器的连接问题。在恢复模式下打开终端(在实用工具菜单中选择终端&a…...

【C/C++】指针常量、常量指针、指向常量的常指针
目录 1.概念2. const pointer3. pointer to a constant3.1 (pointer to a constant)-constant3.2 poiner-constant3.3 (pointer to a constant)-variable3.4 poiner-variable3.5 多层级关系时的兼容3.6 用处 4. a constant pointer to a constant 1.概念 首先明确这几个术语的…...
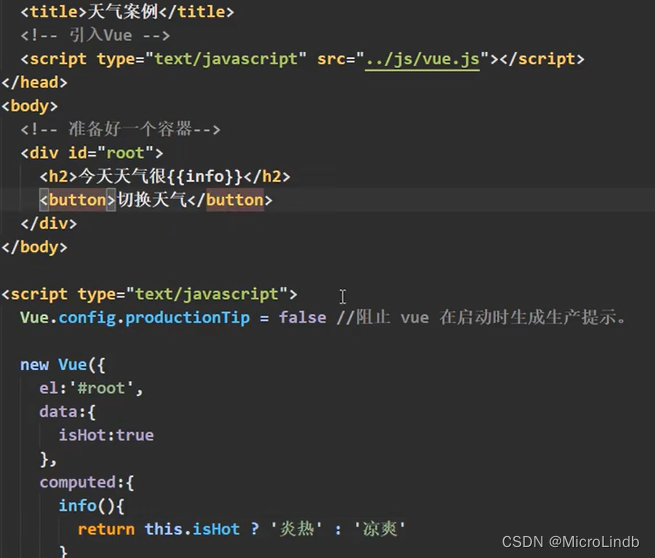
【VUE复习·4】计算属性computed:原理、完整写法(不常用)、与 methods 的区别、简写(最常用)、应用案例!
总览 1.简介计算属性 2.computed 与 methods 的区别 3.computed 的简写(不修改计算属性,只显示) 4.经典应用场景 一、计算属性 1.为什么需要计算属性? 首先,如果我们要写一个插值语法,而 {{ }} 内的内容…...

Linux 基本语句_编译C过程
Linux撰写C语言并编译的过程 1、预处理 将所有的#define删除,并且展开所有的宏定义,并且处理所有的条件预编译指令,比如#if #ifdef #elif #else #endif等。处理#include预编译指令,将被包含的文件插入到该预编译指令的位置。删除…...

MYSQL8解压版 windows 主从部署步骤及配置(包含配置文件,教程文件,免积分下载)
MYSQL8解压版 windows 主从部署步骤及配置 一.安装MSYQL 这里只讲大概,详细步骤、my.ini文件、安装包等会在页尾文件中(正常情况按首个mysql安装,只是名字有区别) 1.主库my.ini配置 [mysqld] #典型的值是5-6GB(8GB内存),8-11GB(16GB内存), 20-25GB(32GB内存)&…...

RabbitMQ的基本介绍
什么是MQ 本质是一个队列,只不过队列中存放的信息是message罢了,还是一种跨进程的通信机制,用于上下游传递信息。在互联网架构中,MQ是一种非常常见的上下游“逻辑解耦物理解耦”的消息通信服务。使用了MQ之后,信息发送…...
AI智能视频监控技术如何助力美好乡村建设?
随着城市化发展,很多乡村设施也在逐渐完善,智能监控也成了乡村发展必不可少的一环,智能视频监控应该在乡村建设里如何发挥作用呢? 1、有效提升安全意识 通过在乡村重要区域、公共场所、道路等设置智能视频监控设备,可…...

【网络安全】2023年堡垒机品牌大全
随着大家网络安全意识的增加,随着国家等保政策的严格执行,越来越多的企业开始采购堡垒机。这里就给大家总结了部分堡垒机品牌,让大家参考参考。 2023年堡垒机品牌大全 1、行云堡垒 2、JumpServer 3、安恒 4、骞云 5、齐治 6、阿里云 …...
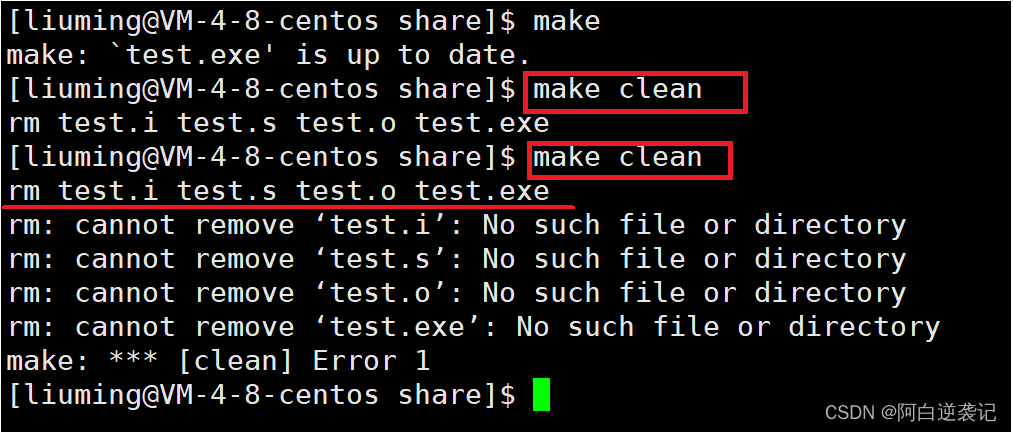
makefile相关知识的讲解
目录 makefile文件的介绍 step1:手动创建一个makefile文件 step2:在文件当中编辑指定的命令 step3:退出makefile文件并使用make执行文件当中的命令 step4:使用clean指令清除生成的文件 makefile当中的命令编写方式 目标文件和依…...
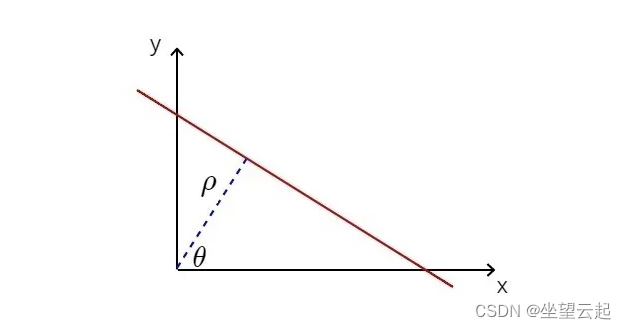
OpenCV中的HoughLines函数和HoughLinesP函数到底有什么区别?
一、简述 基于OpenCV进行直线检测可以使用HoughLines和HoughLinesP函数完成的。这两个函数之间的唯一区别在于,第一个函数使用标准霍夫变换,第二个函数使用概率霍夫变换(因此名称为 P)。概率版本之所以如此,是因为它仅分析点的子集并估计这些点都属于同一条线的概率。此实…...
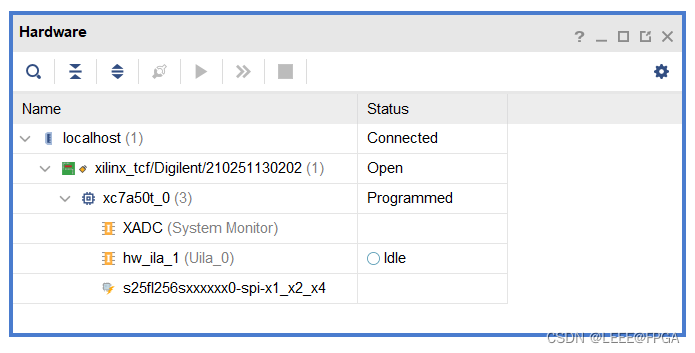
Xilinx FPGA 程序固化重新上电程序不运行的问题
问题描述 FPGA直接下载bit文件,功能正常。 FPGA擦除FLASH,烧写FLASH,正常。 电源断电,重新上电,FALSH里面的程序没有启动,FPGA程序没有跑起来。–FLASH启动不正常。 解决办法 在XDC约束文件里边增加约束: ## Configuration options, can be used for all designs se…...
c++ 使用rapidjson对数据序列化和反序列化(vs2109)
RapidJSON是腾讯开源的一个高效的C JSON解析器及生成器,它是只有头文件的C库,综合性能是最好的。 1. 安装 在NuGet中为项目安装tencent.rapidjson 2. 引用头文件 #include <rapidjson/document.h> #include <rapidjson/memorystream.h> #…...

4.迭代最近点ICP及非线性优化求解
使用非线性优化方法求解ICP 文章目录 使用非线性优化方法求解ICP前情提要ICP问题回顾对矩阵变量求导数 ICP问题的非线性解法代码示例 欢迎访问个人网络日志🌹🌹知行空间🌹🌹 前情提要 在迭代最近点算法ICP及SVD求解中介绍了ICP问…...
【redis总结】
文章目录 1、redis简介2、为什么要选择redis做缓存3、数据结构4、redis多线程模型redis6.0的变化 5、redis持久化AOF的实现过程RDB的实现过程 6、redis集群的搭建7、 redis过期删除和淘汰策略8、redis的内存淘汰策略 1、redis简介 Redis(Remote Dictionary Server&…...

图数据库:释放关系的力量
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 在数据管理领域,图数据库已经成为一种强大的工具,它彻底改变了我们处理和分析复杂关系的方式。与依赖表和列的传统关系数据库不同,图…...

Windows系统如何临时关闭“Windows安全中心实时保护”
前言 启动windows depender实时保护可能会使系统不太流畅,也可能会导致我们的程序无法正常运行,因为它会拦截或搜索我们的正常工作。 暂时关闭windows depender的实时保护对许多用户来说非常重要。 一、Win10系统关闭方法 打开Windows安全中心&#…...
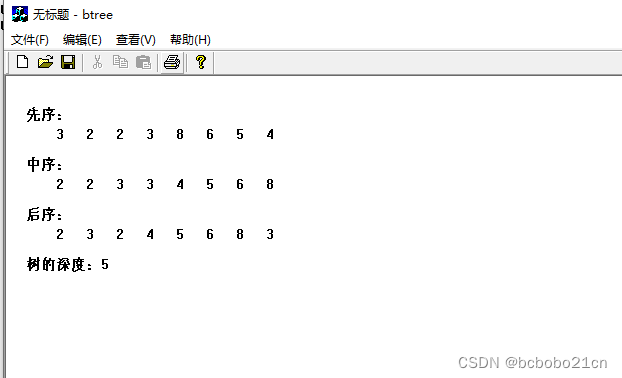
二叉树MFC实现
设有一颗二叉树如下; 这似乎是一颗经常用作示例的二叉树; 对树进行遍历的结果是, 先序为:3、2、2、3、8、6、5、4, 中序为:2、2、3、3、4、5、6、8, 后序为2、3、2、4、5、6、8、3;…...

Nginx之客户并发数限制解读
目录 基本介绍 配置指令 limit_conn_zone limit_conn 其他 limit_rate limit_rate_after limit_req_zone limit_req 基本介绍 在我们进行系统开发设计中,要考虑服务器流量异常,负载过大等问题。对于大流量恶意的攻击访问,会带来带宽…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...
