代码随想录 Day - 51|#309 最佳买卖股票时机含冷冻期|#714 买卖股票的最佳时机含手续费
清单
● 309.最佳买卖股票时机含冷冻期
● 714.买卖股票的最佳时机含手续费
LeetCode #309 最佳买卖股票时机含冷冻期
1. 题目
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
2. 思路
- dp数组含义: dp[i][j] 为第i天所能获取的最大利润, i 代表天数, j代表交易状态。 存在四种交易状态: 1. 买入 2. 保持卖出 3. 卖出 4. 冷冻期
- 递推公式:
1) 买入: dp[i][0] = max(dp[i-1][0], max(dp[i-1][3], dp[i-1][1]) - prices[i])
2) 保持卖出: dp[i][1] = max(dp[i-1][1], dp[i-1][3])
3) 卖出: dp[i][2] = dp[i-1][0] + prices[i]
4) 冷冻期: dp[i][3] = dp[i-1][2] - 初始化 dp[0][0] = - prices[0]
- 正序遍历
3. 代码实现
class Solution:def maxProfit(self, prices: List[int]) -> int:l = len(prices)#Initial dpdp = [[0] * 4 for _ in range(l)]#Original Settingdp[0][0] = - prices[0]for i in range(1, l):dp [i][0] = max(dp[i-1][0], max(dp[i-1][3], dp[i-1][1]) - prices[i])dp [i][1] = max(dp[i-1][1], dp[i-1][3])dp [i][2] = dp[i-1][0] + prices[i]dp [i][3] = dp[i-1][2]return max(dp[l-1][1], dp[l-1][2], dp[l-1][3])
LeetCode #714 买卖股票的最佳时机含手续费
1. 题目
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费
2. 思路
- dp数组含义: dp[i][j] 为第i天所能获取的最大利润, i 代表天数, j代表交易状态。 存在四种交易状态: 1. 买入 2. 卖出
- 递推公式:
1) 买入: dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])
2) 卖出: dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i] - fee) - 初始化 dp[0][0] = - prices[0]
- 正序遍历
3. 代码实现
class Solution:def maxProfit(self, prices: List[int], fee: int) -> int:l = len(prices)#Initial DPdp = [[0] * 2 for _ in range(l)]#Original Settingdp[0][0] = - prices[0]for i in range(1,l):dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i] - fee)return max(dp[-1][1], dp[-1][0])
相关文章:

代码随想录 Day - 51|#309 最佳买卖股票时机含冷冻期|#714 买卖股票的最佳时机含手续费
清单 ● 309.最佳买卖股票时机含冷冻期 ● 714.买卖股票的最佳时机含手续费 LeetCode #309 最佳买卖股票时机含冷冻期 1. 题目 给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。 设计一个算法计算出最大利润。在满足以下约束条件下,你可…...

.net 使用IL生成代理类实现AOP对比Java Spring Boot的AOP
首先,我们需要定义一个接口,代表我们要代理的目标对象的功能: // 日志记录器接口 public interface ILogger {/// <summary>/// 记录日志/// </summary>/// <param name"message">日志消息</param>void L…...
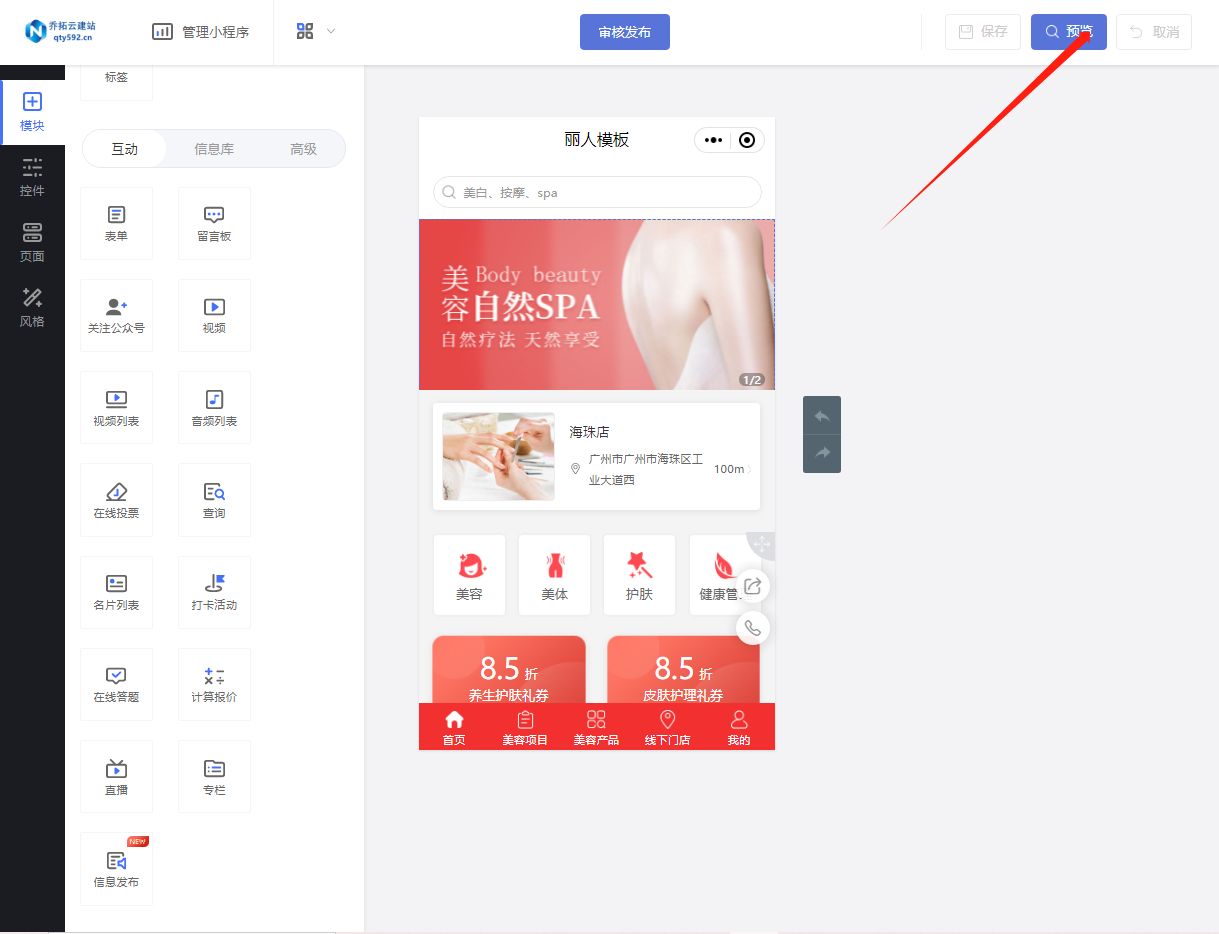
美容店预约小程序搭建流程
随着科技的不断发展,小程序已经成为了人们生活中不可或缺的一部分。对于美容店来说,搭建一个预约小程序不仅可以提高工作效率,还可以增加客户数量、提高服务质量。那么,如何搭建一个美容店预约小程序呢?本文将为你详细…...
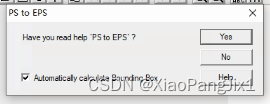
ppt 作图 如何生成eps格式
需求 ppt中画的图,按照eps格式导出。 环境 软件: ppt, Gsview(用来将ps格式转成eps), Adobe 操作系统: win11 思路 直接在ppt里选择adobe打印机,将图片以文件形式打印到ps格式的文件中,再由gsview转化成eps。 建议在本身就…...
渗透测试中的前端调试(上)
一、前言 前端调试是安全测试的重要组成部分。它能够帮助我们掌握网页的运行原理,包括js脚本的逻辑、加解密的方法、网络请求的参数等。利用这些信息,我们就可以更准确地发现网站的漏洞,制定出有效的攻击策略。前端知识对于安全来说ÿ…...

跨境电商引流之Reddit营销,入门保姆级攻略
在当今竞争激烈的在线市场中,企业不断寻求新的方法来加强其数字营销工作。Reddit 是最受欢迎的社交媒体平台之一,为企业提供了巨大的潜力,可以通过引人入胜且相关的内容来接触目标受众。然而,将 Reddit 用于营销目的需要仔细考虑某…...

Linux下虚拟网卡的基本命令
文章目录 创建虚拟网卡查看虚拟网卡删除虚拟网卡 创建虚拟网卡 # 创建tap模式的虚拟网卡tap0 sudo ip tuntap add mode tap tap0 # 开启网卡 sudo ip link set tap0 up # 设置网卡的ip地址和子网掩码 sudo ip addr add 192.168.1.1/24 dev tap0查看虚拟网卡 # 查看虚拟网卡ta…...

conan入门(二十七):因profile [env]字段废弃导致的boost/1.81.0 在aarch64-linux-gnu下交叉编译失败
今天在尝试用conan 1.60.0使用aarch64-linux-gnu编译器交叉编译boost/1.81.0时报错了: conan install boost/1.81.0 -pr:h aarch64-linux-gnu.jinja -pr:b default --build boost输出如下: Configuration (profile_host): [settings] archarmv8 arch_b…...
BFS专题7 多终点迷宫问题
题目: 样例: 输入 3 3 0 0 0 1 0 0 0 1 0 输出 0 1 2 -1 2 3 -1 -1 4 思路: 单纯的 BFS 迷宫问题,只是标记一下每个点的 step,注意初始化答案数组都为 -1. 代码详解如下: #include <iostream> #…...

ES6中对象新增了哪些扩展?
一、属性的简写 当对象字面量的属性名与变量名相同时,可以省略属性名,直接使用变量名作为属性名。 const x 10; const y 20;// ES6之前 const obj1 { x: x, y: y };// ES6属性简写 const obj2 { x, y };注意:简写的对象方法不能用作构造…...

蓝桥杯每日一题2023.9.22
4960. 子串简写 - AcWing题库 题目描述 题目分析 原本为纯暴力但是发现会超时,可以加入前缀和,从前往后先记录一下每个位置c1出现的次数 再从前往后扫一遍,如果遇到c2就将答案加上此位置前的所有c1的个数(直接加上此位置的前缀…...

vscode左键无法跳转到定义的文件
之前用vscode的时候,明明是可以ctrl键鼠标左键跳转到定义文件的,突然之间就不行了,鼠标移到引入上根本都没有下划线,无法跳转 解决方法: 项目的根目录新建 jsconfig.json 文件,代码如下 {"compiler…...
)
c、c++排序的相关知识(归并排序、计数排序、稳定性等)
排序,是对给定的一组数,按照某种逻辑关系,进行位置上的移动。由于排序至少需要将所有数过一遍(正常情况下,非特殊数组),因此排序的时间复杂度一定不能小于O(N)。 归并排…...

oracle定时任务的使用
常见错误: PLS-00225: subprogram or cursor xxx reference is out of scope # job名字太长PLS-00201: identifier COUNT_JOB.SUBMIT must be declared # DBMS_JOB.SUBMIT是固定写法创建存储过程 -- 建表 CREATE TABLE TEST_A(TEST_ADD_DATA DATE); -- 存储过程 C…...
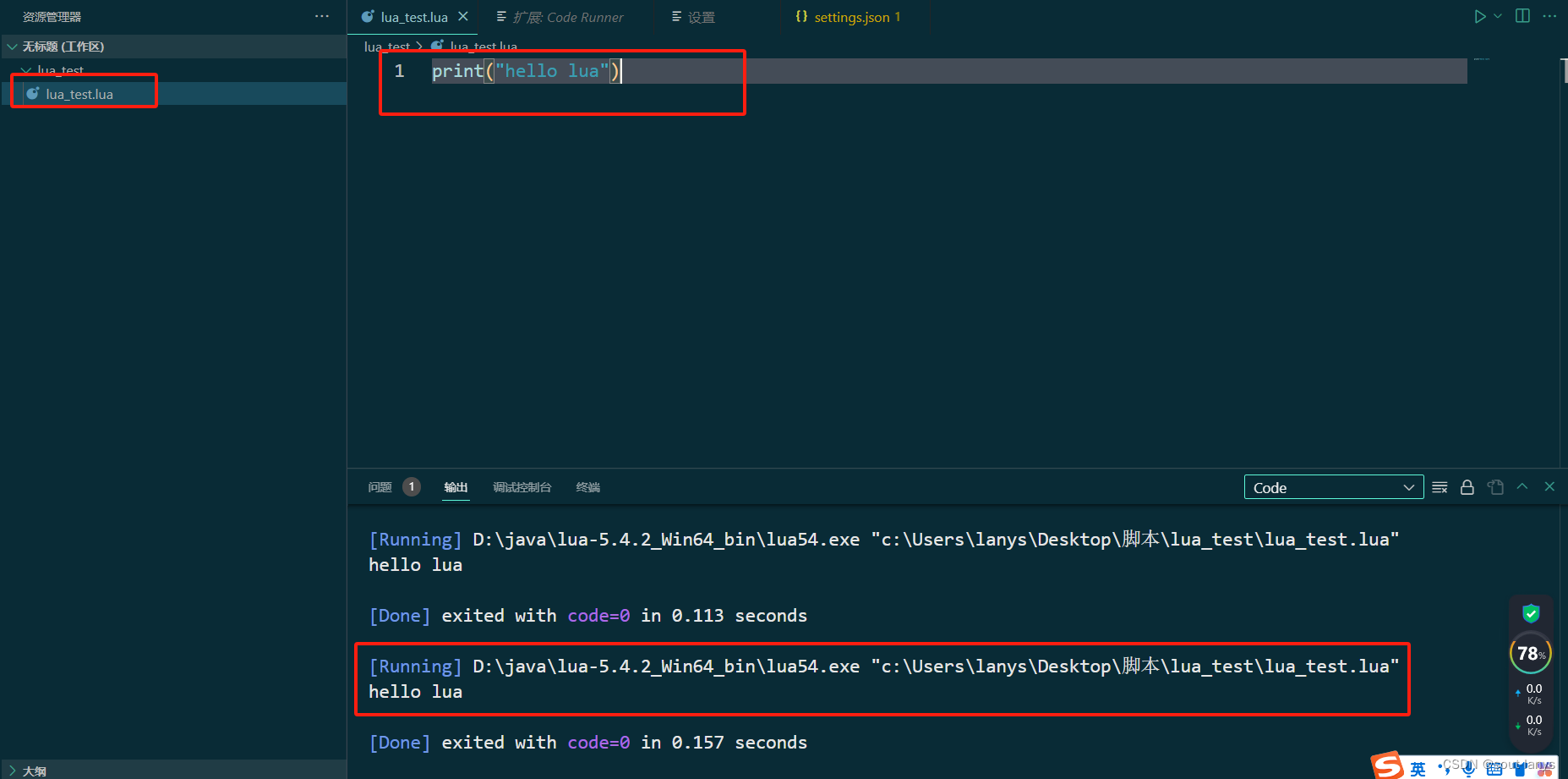
VSCode 配置 Lua 开发环境(清晰明了)
概述 由于 AutoJS 学得已经差不多了,基本都会了,现在开始向其他游戏脚本框架进发, Lua 语言很强大,就不多说, 按键精灵、触动精灵等等都是用该语言编程脚本的,由于按键精灵、触动精灵 和 AutoJS 类似,不是…...

JS合并2个远程pdf
要在HTML和JavaScript中读取远程PDF文件的矢量数据并合并两个PDF文件,您可以使用pdf-lib和Axios库。以下是使用pdf-lib和Axios在HTML和JavaScript中读取和合并远程PDF文件的步骤: 1. 引入 首先,确保您在HTML文件中引入了pdf-lib和Axios库。…...

TikTok的伦理挑战:虚拟世界与现实世界的交汇
在数字时代,社交媒体平台已经不再只是一个信息传播的工具,它已经深刻地改变了我们的社交行为、价值观和伦理观。 而在这一领域的佼佼者之一,TikTok,正面临着伦理挑战,这是虚拟世界与现实世界交汇的产物。 本文将深入…...

C# 获取磁盘空间大小的方法
方法一:利用System.IO.DriveInfo.GetDrives方法来获取 /// 获取指定驱动器的空间总大小(单位为B)////// 只需输入代表驱动器的字母即可 (大写)///public static long GetHardDiskSpace(string str_HardDiskName){long totalSize new long();…...

JVM机制理解与调优方案
作者:逍遥Sean 简介:一个主修Java的Web网站\游戏服务器后端开发者 主页:https://blog.csdn.net/Ureliable 觉得博主文章不错的话,可以三连支持一下~ 如有需要我的支持,请私信或评论留言! 前言 很多Java开发…...
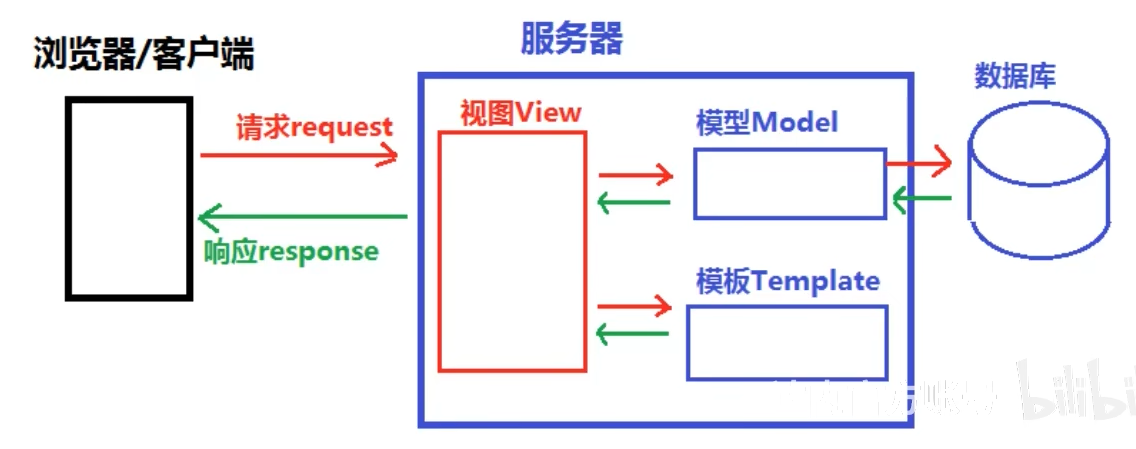
Django的设计模式及模板层
Django的设计模式及模板层 设计模式MVC和MVT MVC 代表 Model-View-Controller(模型-视图-控制器)模式。 M 模型层(Model),主要用于对数据库层的封装 V 视图层(View),用于向用户展示结果 (WHAT HOW) C 控制(Controller,用于处理请求、获取数据、返回结果(重要) 作…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
