【算法分析与设计】动态规划(上)
目录
- 一、学习要点
- 二、算法总体思想
- 三、动态规划基本步骤
- 四、矩阵连乘问题
- 4.1 完全加括号的矩阵连乘积
- 4.2 穷举法
- 4.3 动态规划
- 4.3.1 分析最优解的结构
- 4.3.2 建立递归关系
- 4.3.3 计算最优值
- 4.3.4 用动态规划法求最优解
- 五、动态规划算法的基本要素
- 5.1 最优子结构
- 5.2 重叠子问题
- 5.3 备忘录方法
- 六、思考题:捡硬币问题
一、学习要点
理解动态规划算法的概念。
掌握动态规划算法的基本要素:
(1)最优子结构性质
(2)重叠子问题性质
掌握设计动态规划算法的步骤:
(1)找出最优解的性质,并刻划其结构特征。
(2)递归地定义最优值。
(3)以自底向上的方式计算出最优值。
(4)根据计算最优值时得到的信息,构造最优解。
通过应用范例学习动态规划算法设计策略。
(1)矩阵连乘问题;
(2)最长公共子序列;
(3)最大子段和
(4)凸多边形最优三角剖分;
(5)多边形游戏;
(6)图像压缩;
(7)电路布线;
(8)流水作业调度;
(9)背包问题;
(10)最优二叉搜索树。
二、算法总体思想
动态规划算法与分治法类似,其 基本思想也是将待求解问题分解成若干个子问题。
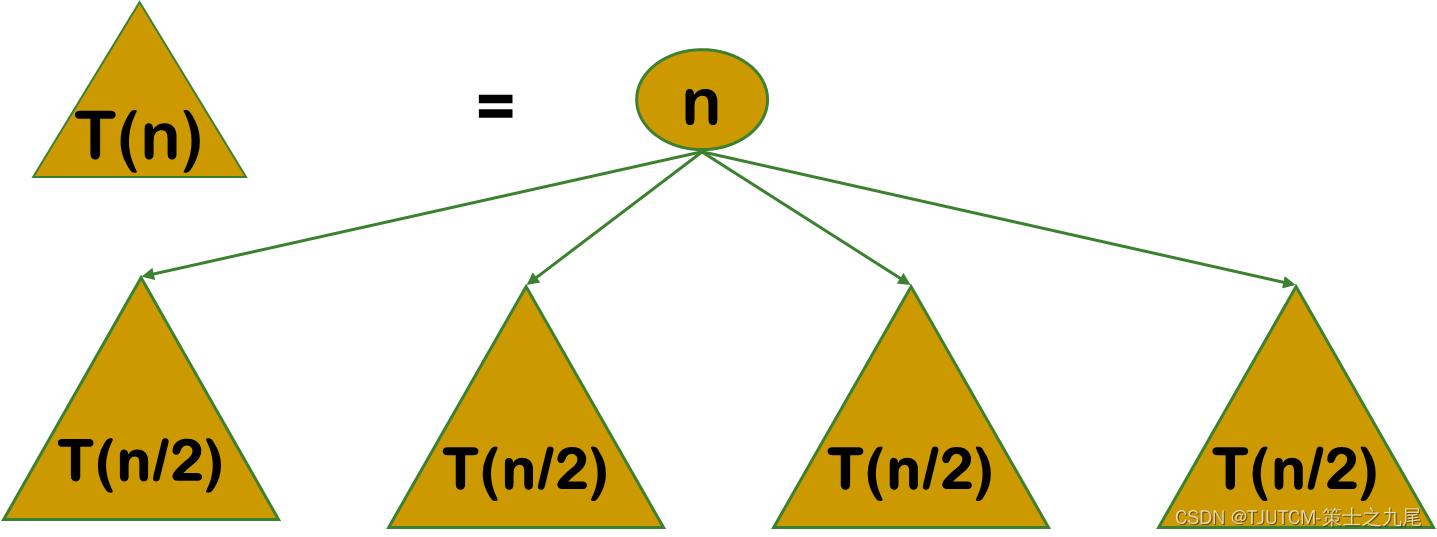
但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时,有些子问题被重复计算了许多次。
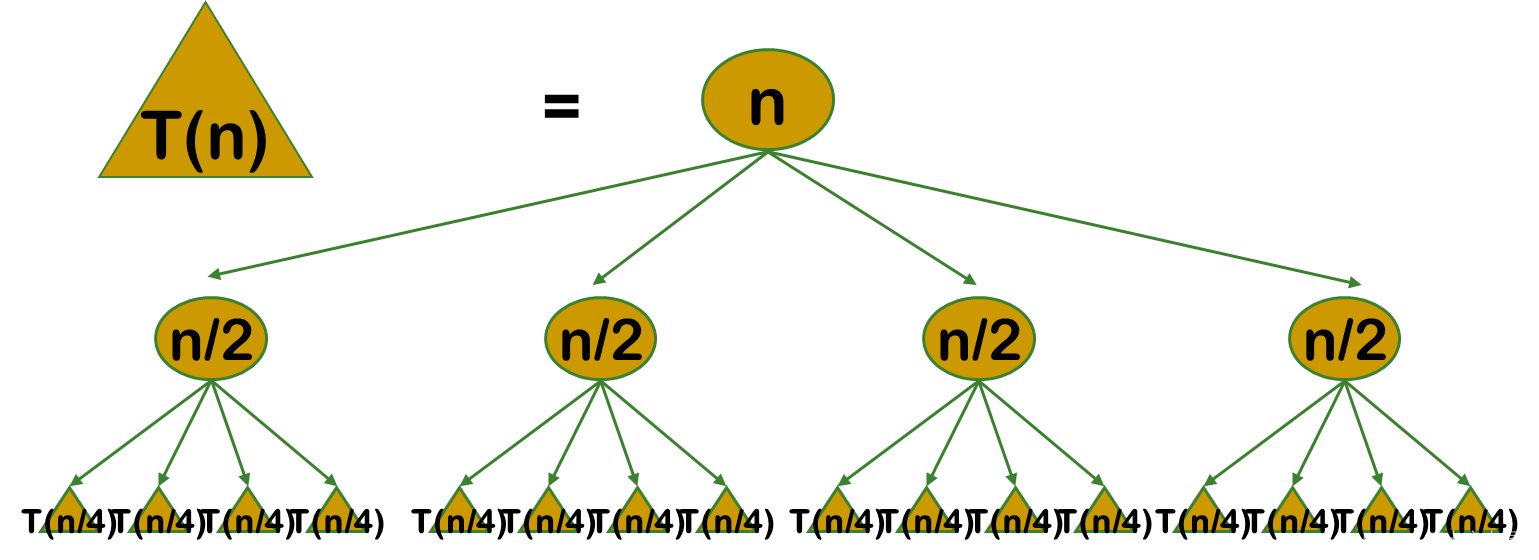
如果 能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法。
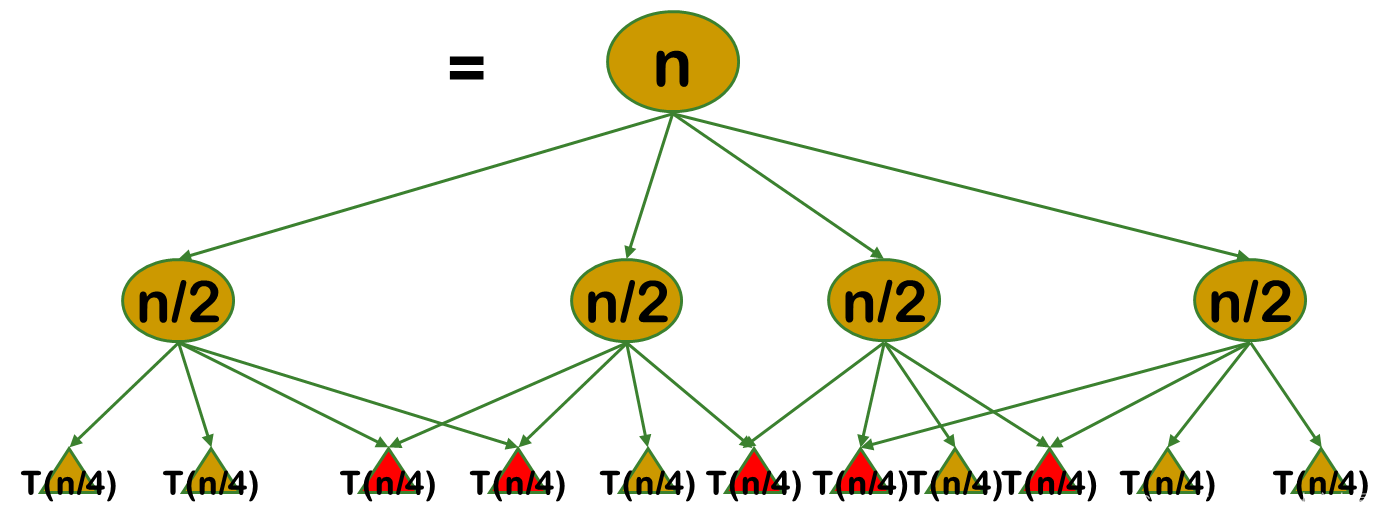
三、动态规划基本步骤
找出最优解的性质,并刻划其结构特征。
递归地定义最优值。
以自底向上的方式计算出最优值。
根据计算最优值时得到的信息,构造最优解。
四、矩阵连乘问题
问题:给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2,…n-1。我们要计算出这 n个矩阵的连乘积。
因为矩阵乘积满足结合律,所以哪两个矩阵先乘哪两个后乘结果是一样的,但是 计算次数不一样,我们要找计算次数最小的那个次序!
4.1 完全加括号的矩阵连乘积
完全加括号的矩阵连乘积可递归地定义为:

设有四个矩阵A,B,C,D;它们的维数分别是:
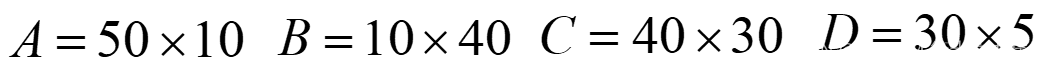
总共有五中完全加括号的方式:
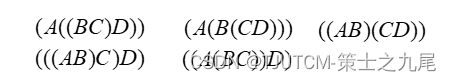
16000, 10500, 36000, 87500, 34500
给定n个矩阵: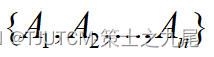 其中Ai与Ai+1是可乘的,i=1,2,…,n-1。考察这n个矩阵的连乘积
其中Ai与Ai+1是可乘的,i=1,2,…,n-1。考察这n个矩阵的连乘积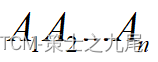
由于 矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2…,n-1。如何确定计算 矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
4.2 穷举法
列举出所有可能的计算次序,并计算出每一种计算次序相应需要的数乘次数,从中找出一种数乘次数最少的计算次序。
算法复杂度分析:
对于n个矩阵的连乘积,设其不同的计算次序为P(n)。
由于每种加括号方式都可以分解为两个子矩阵的加括号问题:(A1…Ak)(Ak+1…An)可以得到关于P(n)的递推式如下:
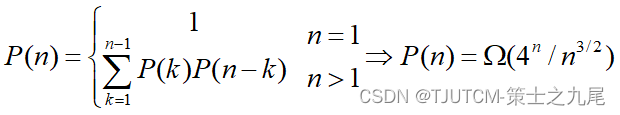
4.3 动态规划
将矩阵连乘积AiAi+1…Aj简记为A[i:j],这里i≤j
考察计算A[i:j]的最优计算次序。设 这个计算次序在矩阵
Ak和Ak+1之间将矩阵链断开,i≤k<j,则其相应完全加括号方式为: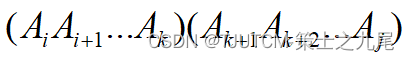
计算量:A[i:k]的计算量加上A[k+1:j]的计算量,再加上A[i:k]和A[k+1:j]相乘的计算量。
4.3.1 分析最优解的结构
特征:计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。
4.3.2 建立递归关系
设计算A[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]
当i=j时,A[i:j]=Ai,因此,m[i,i]=0,i=1,2,…,n
当i<j时,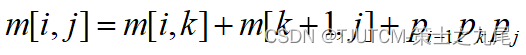

可以递归地定义m[i,j]为:
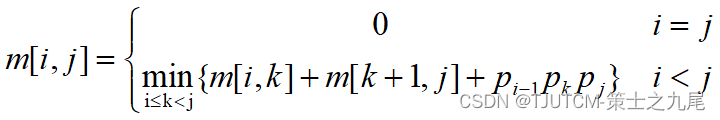
(k的位置只有j-i种可能)
4.3.3 计算最优值
对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问题。因此,不同子问题的个数最多只有
由此可见,在递归计算时,许多子问题被重复计算多次。这也是该问题可用动态规划算法求解的又一显著特征。
用动态规划算法解此问题,可依据其递归式以自底向上的方式进行计算。在计算过程中,保存已解决的子问题答案。每个子问题只计算一次,而在后面需要时只要简单查一下,从而避免大量的重复计算,最终得到多项式时间的算法。

1.计算A1,A2,A3,A4,A5,A6
2.计算(A1A2),(A2A3),(A3A4),(A4A5),(A5A6)
3.计算(A1A2A3),…,(A4A5A6)
4.计算A[1,4],A[2,5],A[3,6]
5.计算A[1,5],A[2,6]
6.计算A[1,6]
4.3.4 用动态规划法求最优解
void MatrixChain(int *p,int n,int **m,int **s)
{for (int i = 1; i <= n; i++) m[i][i] = 0;for (int r = 2; r <= n; r++)for (int i = 1; i <= n - r+1; i++) {int j=i+r-1;m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];s[i][j] = i;for (int k = i+1; k < j; k++) {int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}}}
}

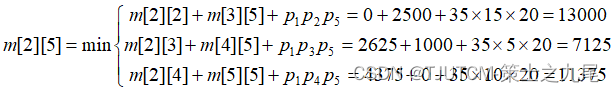
算法复杂度分析:
算法matrixChain的主要计算量取决于算法中对r,i和k的3重循环。循环体内的计算量为O(1),而3重循环的总次数为O(n3)。因此算法的计算时间上界为O(n3)。算法所占用的空间显然为O(n2)。

五、动态规划算法的基本要素
5.1 最优子结构
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
在分析问题的最优子结构性质时,所用的方法具有普遍性:首先假设由问题的最优解导出的子问题的解不是最优的,然后再设法说明在这个假设下可构造出比原问题最优解更好的解,从而导致矛盾。
利用问题的最优子结构性质,以自底向上的方式 递归地从子问题的最优解逐步构造出整个问题的最优解。最优子结构是问题能用动态规划算法求解的前提。
同一个问题可以有多种方式刻划它的最优子结构,有些表示方法的求解速度更快(空间占用小,问题的维度低)
5.2 重叠子问题
递归算法求解问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。这种性质称为子问题的重叠性质。
动态规划算法,对每一个子问题只解一次,而后将其解保存在一个表格中,当再次需要解此子问题时,只是简单地用常数时间查看一下结果。
通常不同的子问题个数随问题的大小呈多项式增长。因此用动态规划算法只需要多项式时间,从而获得较高的解题效率。
5.3 备忘录方法
备忘录方法的控制结构与直接递归方法的控制结构相同,区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解。
int LookupChain(int i,int j)
{if (m[i][j] > 0) return m[i][j];if (i == j) return 0;int u = LookupChain(i,i) + LookupChain(i+1,j) + p[i-1]*p[i]*p[j];s[i][j] = i;for (int k = i+1; k < j; k++) {int t = LookupChain(i,k) + LookupChain(k+1,j) + p[i-1]*p[k]*p[j];if (t < u) { u = t; s[i][j] = k;}}m[i][j] = u;return u;
}
六、思考题:捡硬币问题
现有n个硬币按顺序依次排列在你面前,可以看为一个数组coins[]={5,1,2,10,6,2},请在此中捡取若干个硬币,使得所取硬币累加值最大,捡取个数不限,但相邻两个硬币不得捡取,请设计相应算法,并输出累加值
提示:硬币面值必须是正数,不能有负值。建立数组dp[i]存储选取前i个硬币的累加值
相关文章:

【算法分析与设计】动态规划(上)
目录 一、学习要点二、算法总体思想三、动态规划基本步骤四、矩阵连乘问题4.1 完全加括号的矩阵连乘积4.2 穷举法4.3 动态规划4.3.1 分析最优解的结构4.3.2 建立递归关系4.3.3 计算最优值4.3.4 用动态规划法求最优解 五、动态规划算法的基本要素5.1 最优子结构5.2 重叠子问题5.…...
Java多线程篇(6)——AQS之ReentrantLock
文章目录 1、管程2、AQS3、ReentrantLock3.1、lock/unlock3.1.1、lock3.1.2、unlock 3.2、一些思考 1、管程 什么是管程? 管理协调多个线程对共享资源的访问,是一种高级的同步机制。 有哪些管程模型? hansen:唤醒其他线程的代码…...

【计算机网络】IP协议第二讲(Mac帧、IP地址、碰撞检测、ARP协议介绍)
IP协议第二讲 1.IP和Mac帧2.碰撞检测2.1介绍2.2如何减少碰撞发生2.3MTU2.4一些补充 3.ARP协议3.1协议介绍3.2报文格式分析 1.IP和Mac帧 IP(Internet Protocol)和MAC(Media Access Control)帧是计算机网络中两个不同层次的概念&am…...
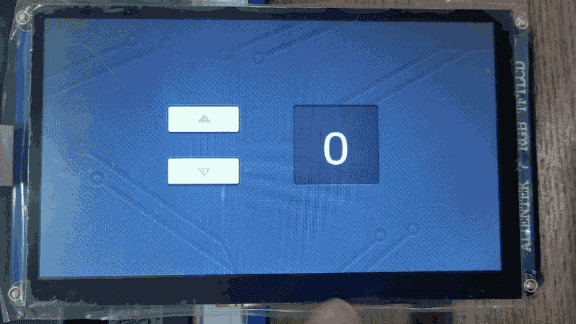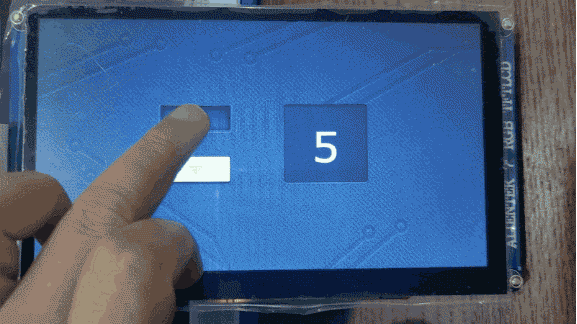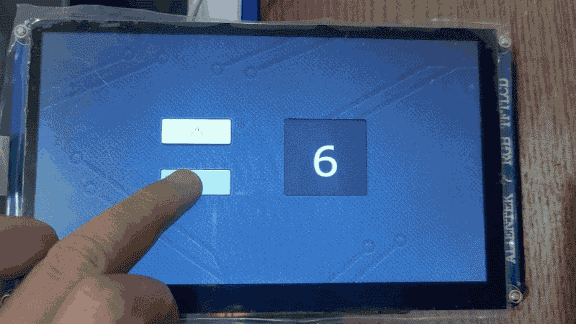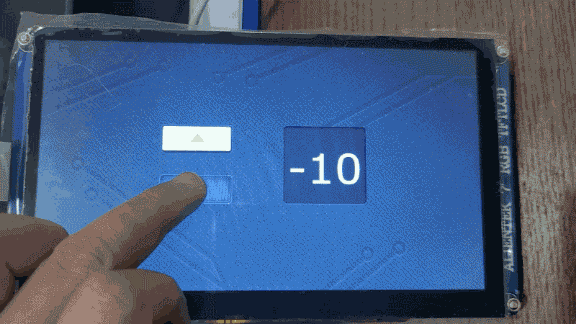
TouchGFX界面开发 | 按钮控件应用示例
按钮控件应用示例 按钮是最常见的部件之一,有了按钮就可以点击,从而响应事件,达到人机交互的目的。TouchGFX Designer内置了七种按钮部件: 下压按钮:能够在被释放时发送回调,按下和释放状态都关联了图像标…...
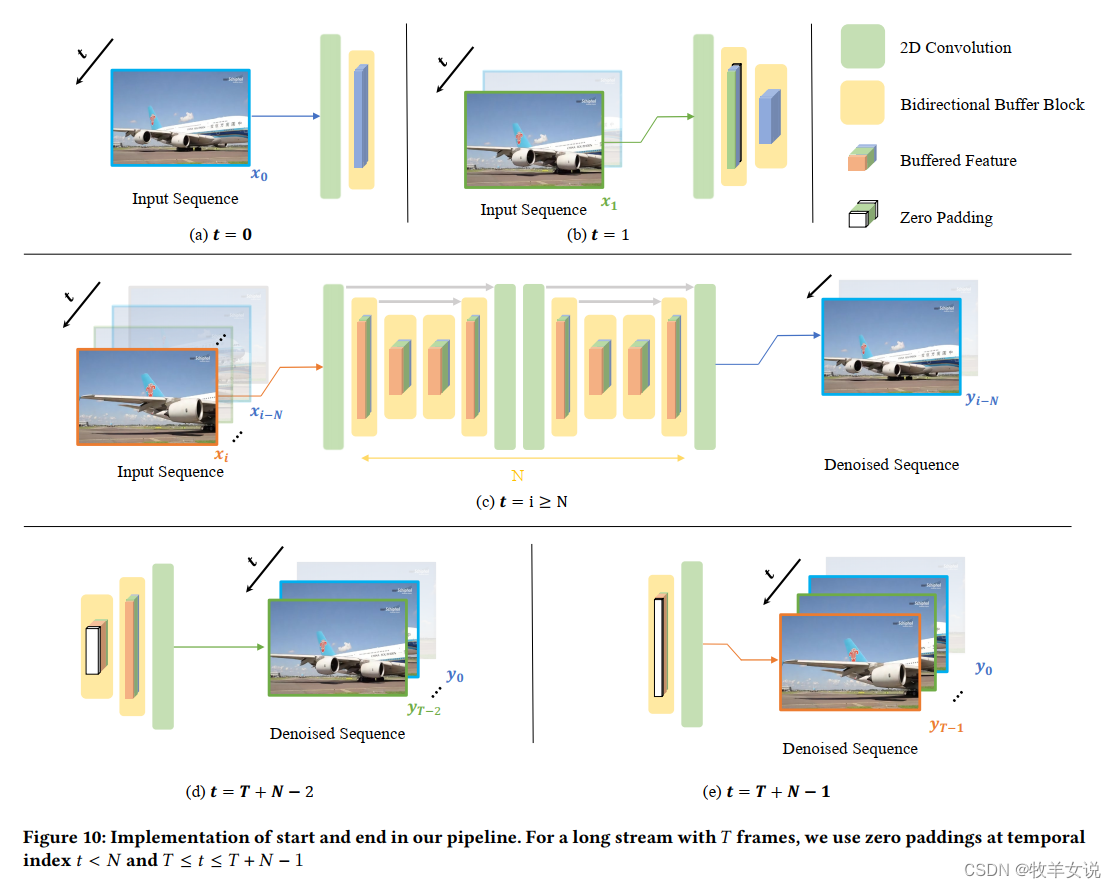
BSVD论文理解:Real-time Streaming Video Denoising with Bidirectional Buffers
BSVD是来自香港科技大学的一篇比较新的视频去噪论文,经实践,去噪效果不错,在这里分享一下对这篇论文的理解。 论文地址:https://arxiv.org/abs/2207.06937 代码地址:GitHub - ChenyangQiQi/BSVD: [ACM MM 2022] Real…...

共同见证丨酷雷曼武汉运营中心成立2周年
酷雷曼武汉运营中心2周年 全国合作商齐贺武汉公司2周年庆 2021年 作为酷雷曼辐射全国版图的又一重要据点 酷雷曼武汉运营中心 在“中国光谷”正式成立 沉浸式参观酷雷曼武汉公司 2年时间 尽管历经诸多客观因素的挑战 但后浪扬帆,依然交出了不斐的成绩 解决…...
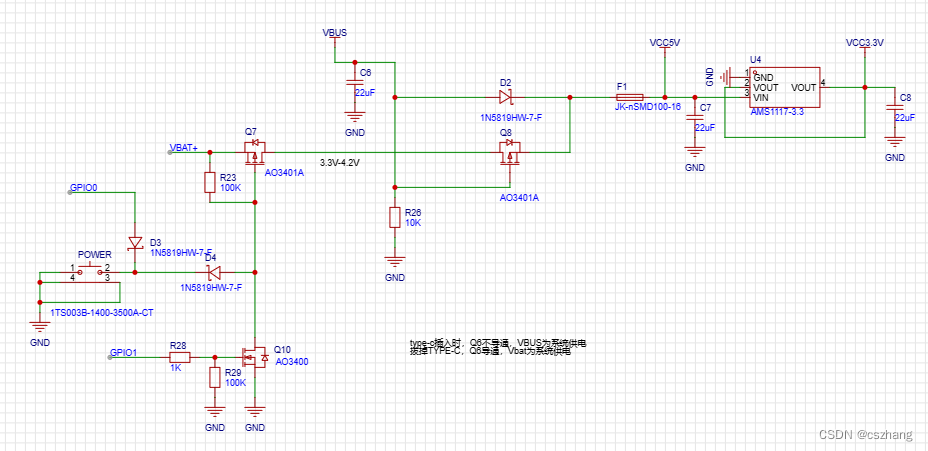
一种单键开关机电路图
我们设计产品时,通常需要设计单键开关机功能。 单键开关机,通常需要单片机的两个IO完成,一个IO用于保持开机状态。另外,一个IO用于判定关机状态。 下面就是一种单键开关机电路原理图: 此单键开关电路已经在S2W-M02、S2…...
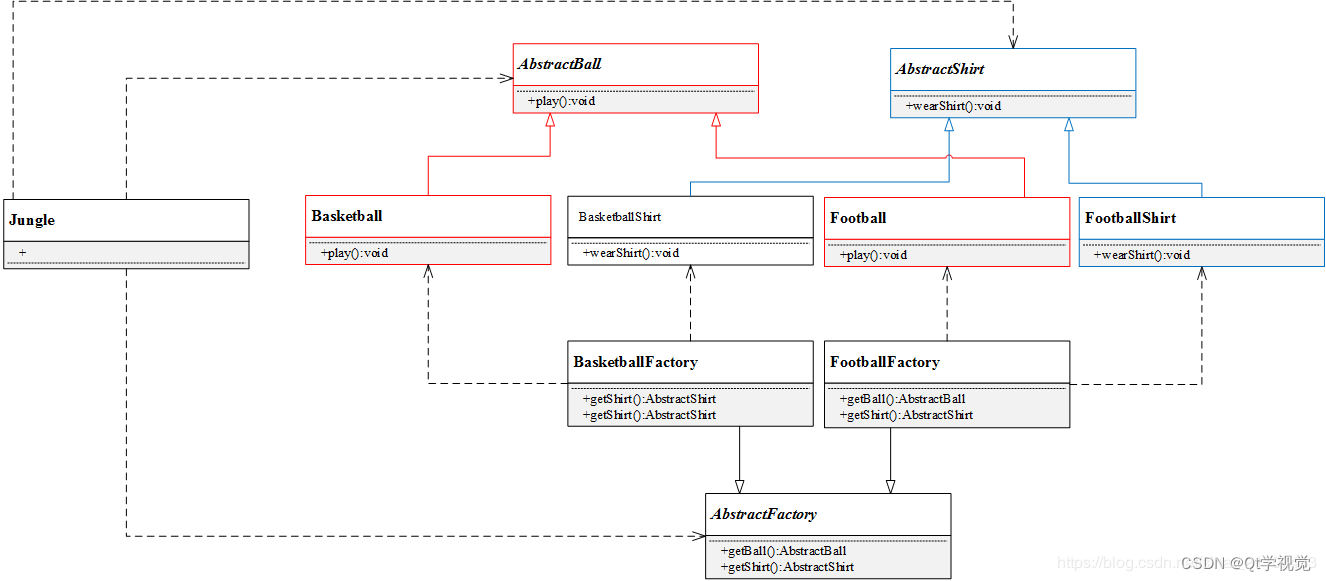
设计模式2、抽象工厂模式 Abstract Factory
解释说明:提供一个创建一系列相关或相互依赖对象的接口,而无需指定他们具体的类。 简言之,一个工厂可以提供创建多种相关产品的接口,而无需像工厂方法一样,为每一个产品都提供一个具体工厂 抽象工厂(Abstra…...

C++ 32盏灯,利用进制和 与 或 进行设计
一共32盏灯,设计一个灯光控制系统,其中 台球部8盏灯 桌游区8盏灯 酒吧区8盏灯 休息区8盏灯 满足以下功能 1、能够独立控制每一盏灯 2、能够一次性打开或关闭一个区域的全部灯光 3、能够获取各个区域的灯光打开关闭情况 4、能够一次性关闭打开的灯&#x…...
-安装:ubuntu系统安装Ffmpeg应用)
Ffmpeg-(1)-安装:ubuntu系统安装Ffmpeg应用
1、下载源码压缩包 https://ffmpeg.org/download.html 点击Download Source Code下载即可 解压: tar -xvjf ffmpeg-snapshot.tar.bz2 得到:ffmpeg目录 cd ffmpeg 或者:直接下 wget http://www.ffmpeg.org/releases/ffmpeg-5.1.tar.gztar -zx…...
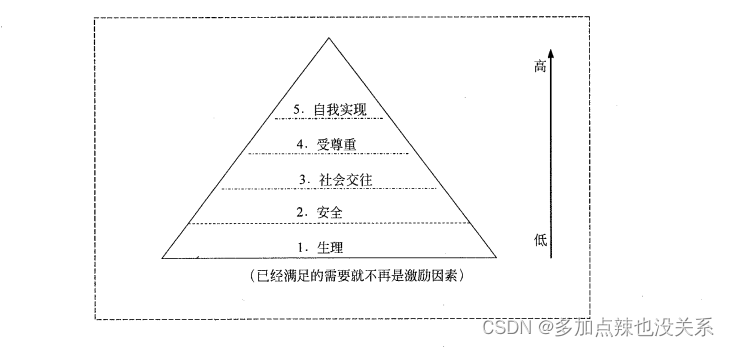
系统集成|第十一章(笔记)
目录 第十一章 项目人力资源管理11.1 项目人力资源管理的定义及有关概念11.2 主要过程11.2.1 编制项目人力资源管理计划11.2.2 组建项目团队11.2.3 建设项目团队11.2.4 管理项目团队 11.3 现代激励理论11.4 项目经理所需具备的影响力11.5 常见问题 上篇:第十章、质量…...
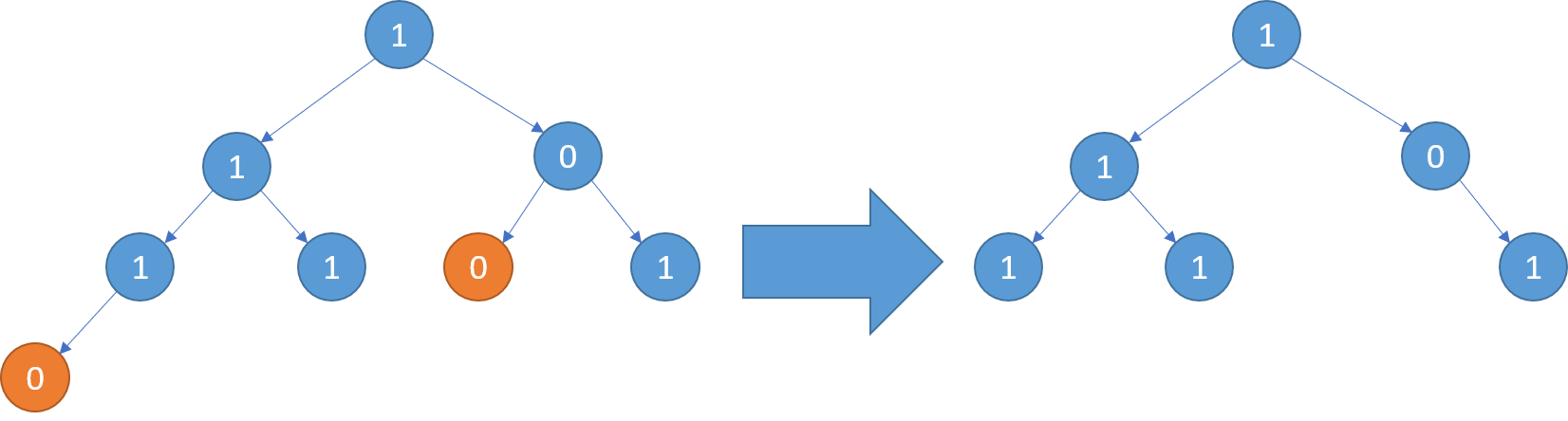
二叉树题目:二叉树剪枝
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:二叉树剪枝 出处:814. 二叉树剪枝 难度 4 级 题目描述 要求 给定二叉树的根结点 root \texttt{root} root,返回移除了所有…...
JAVA中使用CompletableFuture进行异步编程
JAVA中使用CompletableFuture进行异步编程 1、什么是CompletableFuture CompletableFuture 是 JDK8 提供的 Future 增强类,CompletableFuture 异步任务执行线程池,默认是把异步任 务都放在 ForkJoinPool 中执行。 在这种方式中,主线程不会…...

uniapp:配置动态接口域名,根据图片访问速度,选择最快的接口
common.js // 动态测速选择的域名 // h5直接返回默认第一个域名 // vue文件用到域名的话用this.$baseURL let domains [{uri:192.168.31.215:9523, speed:0},{uri:api.ceshi.org, speed:0}, ]export const protocol {api: http://,//本地// api: https://api.,//正式h5Url: h…...
)
Lambda表达式常见用法(提高效率神器)
Java8中一个非常重要的特性就是Lambda表达式,我们可以把它看成是一种闭包,它允许把函数当做参数来使用,是面向函数式编程的思想,一定程度上可以使代码看起来更加简洁。 其实以上都不重要,重要的是能够提高我的开发效率…...

2023旷视自驾感知算法暑期实习一面
来源:投稿 作者:LSC 编辑:学姐 1. 问下项目,问下我的情况 2. 是否了解最新的BEV算法,讲一下 3. 是否了解三维重建 4. 考察相机坐标系的转换 5. 手撕代码,翻车了,不考leetcode,考…...
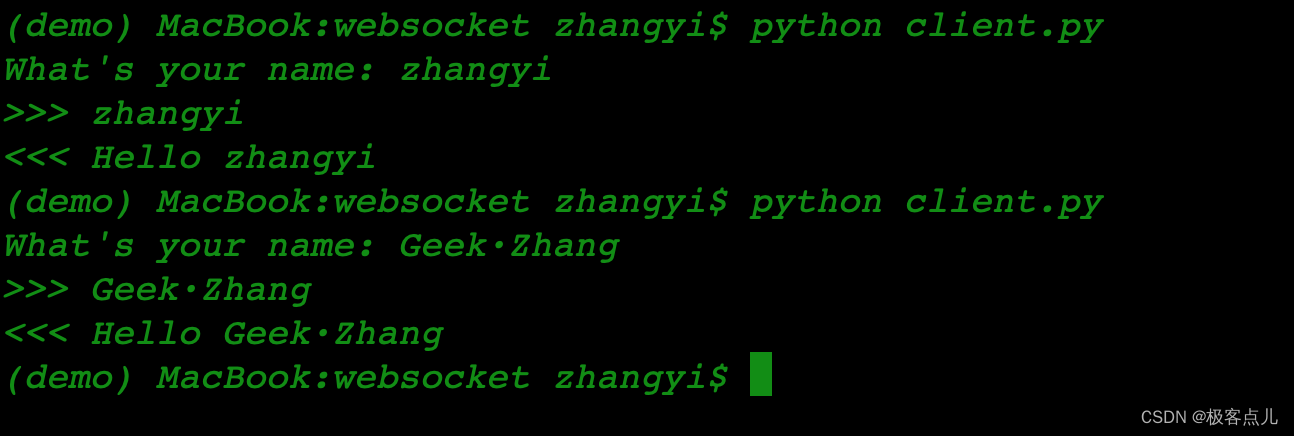
Python3 如何实现 websocket 服务?
Python 实现 websocket 服务很简单,有很多的三方包可以用,我从网上大概找到三种常用的包:websocket、websockets、Flask-Sockets。 但这些包很多都“年久失修”, 比如 websocket 在 2010 年就不维护了。 而 Flask-Sockets 也在 2…...

SQLAlchemy常用数据类型
目录 SQLAlchemy常用数据类型 代码演示 代码分析 SQLAlchemy常用数据类型 SQLAlchemy 是一个Python的SQL工具库和对象关系映射(ORM)工具,它提供了一种在Python中操作数据库的高效方式。下面是SQLAlchemy中常用的一些数据类型: Integer:整形&…...
Vue路由与nodejs下载安装及环境变量的配置
目录 前言 一、Vue路由 1.路由简介 是什么 作用 应用场景 2.SPA简介 SPA是什么 SPA的优点 注意事项 3.路由实现思路 1.引入路由的js依赖 2.定义组件 3.定义组件与路径的对应关系 4.通过路由关系获取路由对象router 5.将路由对象挂载到实例中 6.触发路由事…...
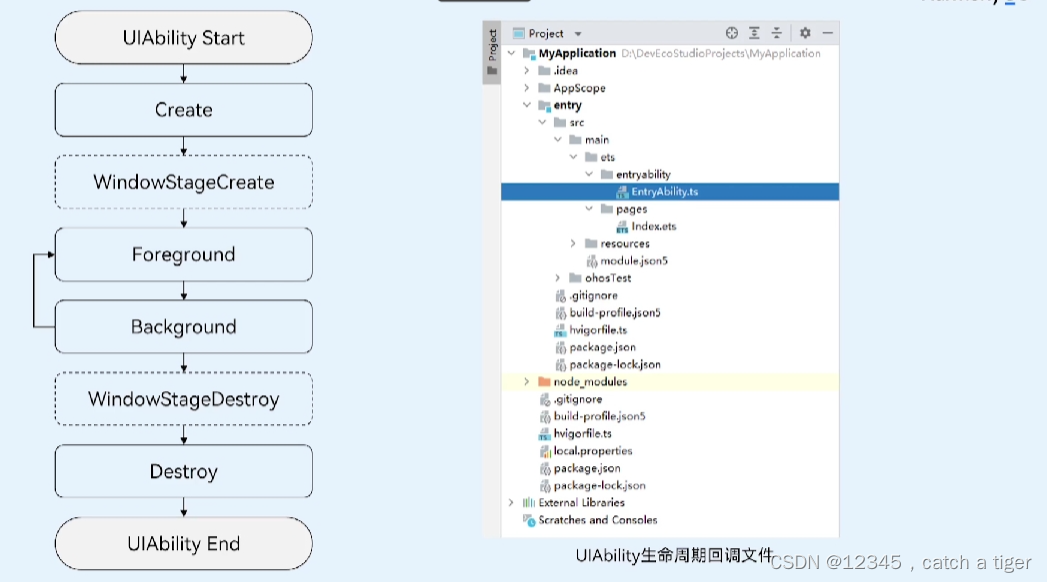
HarmonyOS之 应用程序页面UIAbility
一 UIAbility介绍: 1.1 UIAbility是一种包含用户界面的应用组件,主要用于和用户进行交互 1.2 UIAbility也是系统调度的单元,为应用提供窗口在其中绘制界面 二 UIAbility跳转和传参 2.1 页面间的导航可以通过页面路由router模块来实现。页…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
