二叉树题目:二叉树剪枝
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:二叉树剪枝
出处:814. 二叉树剪枝
难度
4 级
题目描述
要求
给定二叉树的根结点 root \texttt{root} root,返回移除了所有不包含 1 \texttt{1} 1 的子树的原二叉树。
结点 node \texttt{node} node 的子树为 node \texttt{node} node 本身以及所有 node \texttt{node} node 的后代。
示例
示例 1:

输入: root = [1,null,0,0,1] \texttt{root = [1,null,0,0,1]} root = [1,null,0,0,1]
输出: [1,null,0,null,1] \texttt{[1,null,0,null,1]} [1,null,0,null,1]
解释:
只有红色结点满足条件「所有不包含 1 \texttt{1} 1 的子树」。右图为返回的答案。
示例 2:
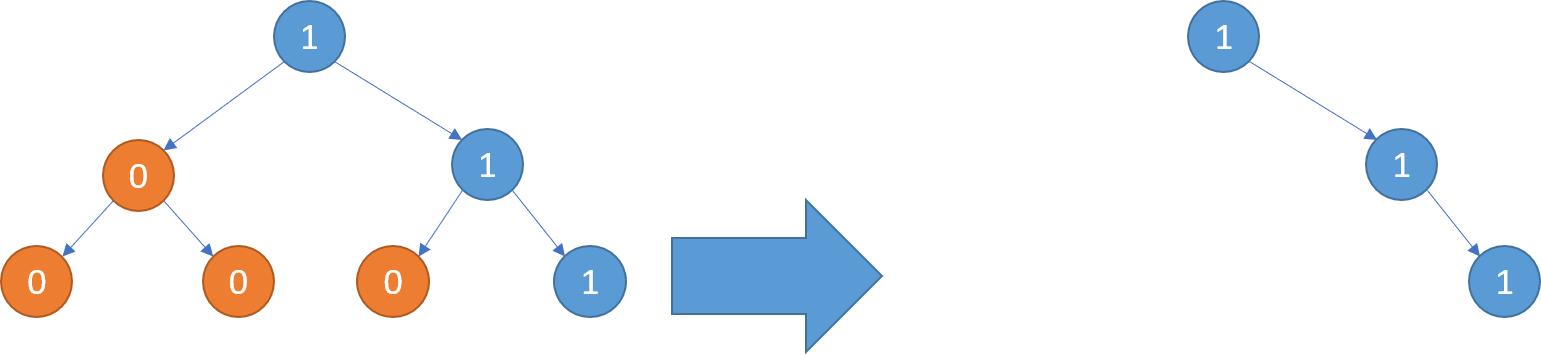
输入: root = [1,0,1,0,0,0,1] \texttt{root = [1,0,1,0,0,0,1]} root = [1,0,1,0,0,0,1]
输出: [1,null,1,null,1] \texttt{[1,null,1,null,1]} [1,null,1,null,1]
示例 3:
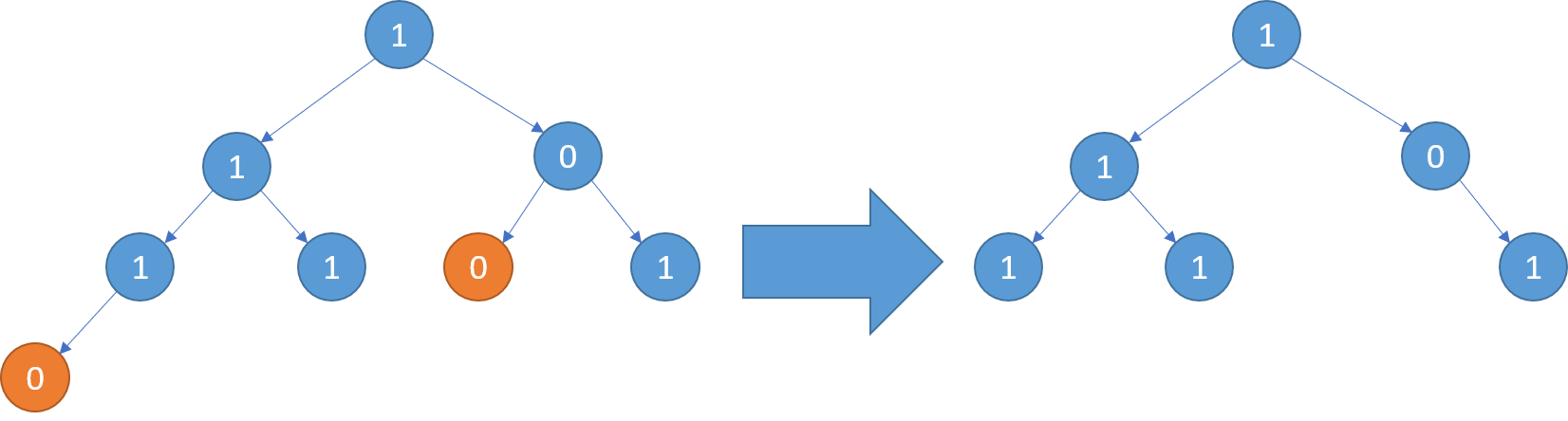
输入: root = [1,1,0,1,1,0,1,0] \texttt{root = [1,1,0,1,1,0,1,0]} root = [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1] \texttt{[1,1,0,1,1,null,1]} [1,1,0,1,1,null,1]
数据范围
- 树中结点数目在范围 [1, 200] \texttt{[1, 200]} [1, 200] 内
- Node.val \texttt{Node.val} Node.val 是 0 \texttt{0} 0 或 1 \texttt{1} 1
解法
思路和算法
如果二叉树为空,则不需要执行剪枝操作,直接返回即可。
当二叉树不为空时,需要首先对二叉树的左子树和右子树执行剪枝操作,然后对当前二叉树执行剪枝操作。剪枝操作具体为,如果一个结点是叶结点且结点值为 0 0 0,则该结点被移除。注意在移除值为 0 0 0 的叶结点之后,被移除的结点的父结点可能从非叶结点变成叶结点。
由于每个结点是否需要被移除和结点的子树有关,因此可以使用深度优先搜索实现。
整个过程是一个递归的过程。递归的终止条件是当前结点为空,或者当前结点是叶结点且结点值为 0 0 0,这两种情况都返回空二叉树。对于其余情况,递归地对左子树和右子树执行剪枝操作。
由于剪枝操作只会移除所有的值为 0 0 0 的叶结点(包括从非叶节点变成叶结点的值为 0 0 0 的结点),不会移除值为 1 1 1 的结点,因此剪枝操作可以确保移除所有不包含 1 1 1 的子树。
代码
class Solution {public TreeNode pruneTree(TreeNode root) {if (root == null) {return root;}root.left = pruneTree(root.left);root.right = pruneTree(root.right);if (root.left == null && root.right == null && root.val == 0) {root = null;}return root;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是递归调用的栈空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。
相关文章:

二叉树题目:二叉树剪枝
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:二叉树剪枝 出处:814. 二叉树剪枝 难度 4 级 题目描述 要求 给定二叉树的根结点 root \texttt{root} root,返回移除了所有…...
JAVA中使用CompletableFuture进行异步编程
JAVA中使用CompletableFuture进行异步编程 1、什么是CompletableFuture CompletableFuture 是 JDK8 提供的 Future 增强类,CompletableFuture 异步任务执行线程池,默认是把异步任 务都放在 ForkJoinPool 中执行。 在这种方式中,主线程不会…...

uniapp:配置动态接口域名,根据图片访问速度,选择最快的接口
common.js // 动态测速选择的域名 // h5直接返回默认第一个域名 // vue文件用到域名的话用this.$baseURL let domains [{uri:192.168.31.215:9523, speed:0},{uri:api.ceshi.org, speed:0}, ]export const protocol {api: http://,//本地// api: https://api.,//正式h5Url: h…...
)
Lambda表达式常见用法(提高效率神器)
Java8中一个非常重要的特性就是Lambda表达式,我们可以把它看成是一种闭包,它允许把函数当做参数来使用,是面向函数式编程的思想,一定程度上可以使代码看起来更加简洁。 其实以上都不重要,重要的是能够提高我的开发效率…...

2023旷视自驾感知算法暑期实习一面
来源:投稿 作者:LSC 编辑:学姐 1. 问下项目,问下我的情况 2. 是否了解最新的BEV算法,讲一下 3. 是否了解三维重建 4. 考察相机坐标系的转换 5. 手撕代码,翻车了,不考leetcode,考…...
Python3 如何实现 websocket 服务?
Python 实现 websocket 服务很简单,有很多的三方包可以用,我从网上大概找到三种常用的包:websocket、websockets、Flask-Sockets。 但这些包很多都“年久失修”, 比如 websocket 在 2010 年就不维护了。 而 Flask-Sockets 也在 2…...

SQLAlchemy常用数据类型
目录 SQLAlchemy常用数据类型 代码演示 代码分析 SQLAlchemy常用数据类型 SQLAlchemy 是一个Python的SQL工具库和对象关系映射(ORM)工具,它提供了一种在Python中操作数据库的高效方式。下面是SQLAlchemy中常用的一些数据类型: Integer:整形&…...
Vue路由与nodejs下载安装及环境变量的配置
目录 前言 一、Vue路由 1.路由简介 是什么 作用 应用场景 2.SPA简介 SPA是什么 SPA的优点 注意事项 3.路由实现思路 1.引入路由的js依赖 2.定义组件 3.定义组件与路径的对应关系 4.通过路由关系获取路由对象router 5.将路由对象挂载到实例中 6.触发路由事…...
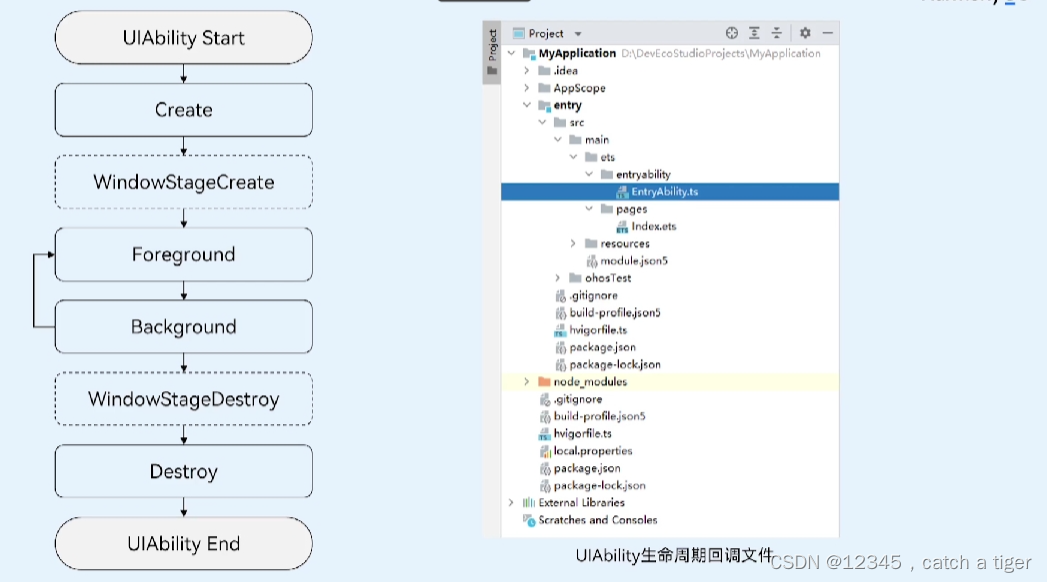
HarmonyOS之 应用程序页面UIAbility
一 UIAbility介绍: 1.1 UIAbility是一种包含用户界面的应用组件,主要用于和用户进行交互 1.2 UIAbility也是系统调度的单元,为应用提供窗口在其中绘制界面 二 UIAbility跳转和传参 2.1 页面间的导航可以通过页面路由router模块来实现。页…...
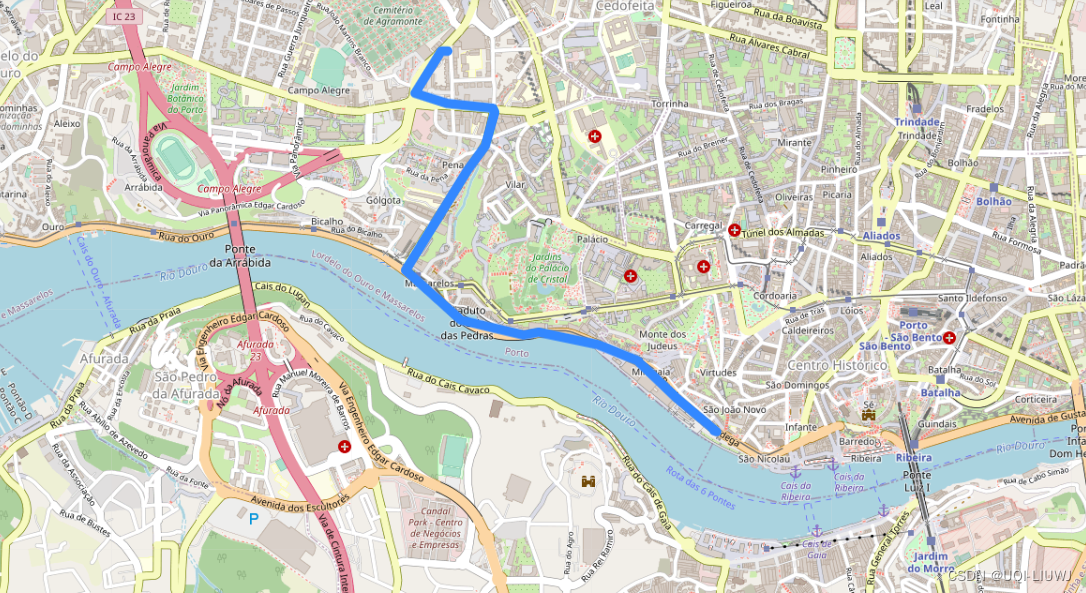
数据集笔记: Porto
数据来源:Taxi Trajectory Data_数据集-阿里云天池 (aliyun.com) 1 数据介绍 葡萄牙波尔图市运行的所有442辆出租车的全年轨迹(从2013年7月1日至2014年6月30日) 2 读取数据 import pandas as pdtrapd.read_csv(C:/Users/16000/Download…...
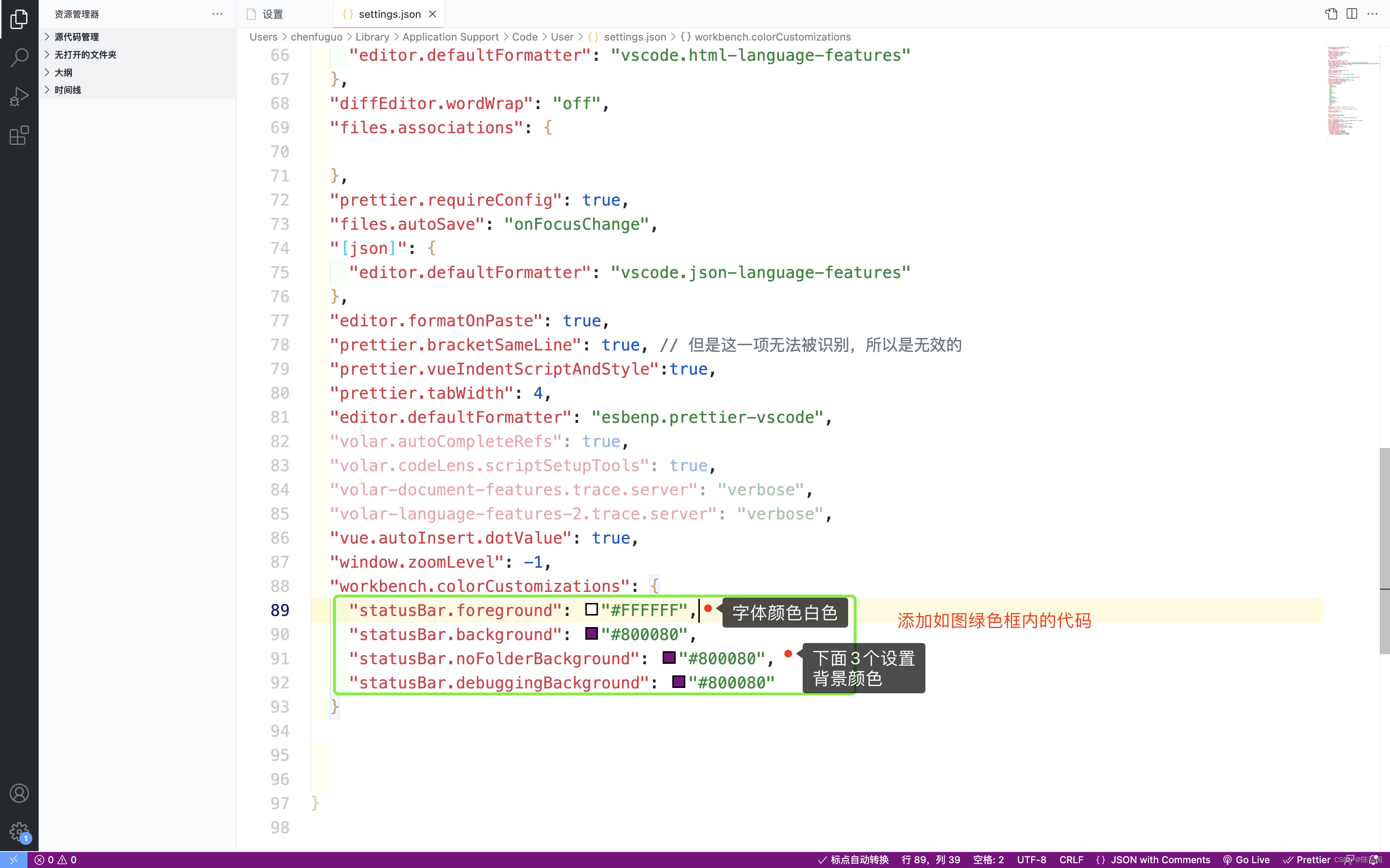
修改vscode底部栏背景和字体颜色
修改vscode底部栏背景和字体颜色 如图: 首先打开齿轮,打开设置搜索workbench.colorCustomizations,然后点击编辑setting.json修改setting.json内内容 "workbench.colorCustomizations": {"statusBar.foreground": "#FFFFFF…...

加速企业AI实施:成功策略和效率方法
文章目录 写在前面面临的挑战MlOps简介好书推荐 写作末尾 写在前面 作为计算机科学领域的一个关键分支,机器学习在当今人工智能领域中占据着至关重要的地位,广受瞩目。机器学习通过深入分析大规模数据并总结其中的规律,为我们提供了解决许多…...
【图论C++】树的重心——教父POJ 3107(链式前向星的使用)
》》》算法竞赛 /*** file * author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * brief 一直在竞赛算法学习的路上* * copyright 2023.9* COPYRIGHT 原创技术笔记:转载…...

hhh百度地铁广告太搞笑了;24家国内大模型公司面经;LLM法律应用实践;AI+教育产品图谱与工作流 | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🔥 会玩儿!承包地铁专列,真人移动广告 | 百度世界大会预热 百度也是会玩儿!承包了北京地铁一号线的「…...

项目管理:项目经理一定要避开这四大误区
项目经理要保质保量按时达成项目目标,需要关注项目的方方面面,要具有很强的沟通协调能力和目标意识。但是项目经理也不免不了失误,管理中的这四大误区,你经历过几个? 误区一:做不该做的事 你是否遇到这种…...

爬虫为什么需要 HTTP 代理 IP?
前言 爬虫在互联网数据采集、分析和挖掘中扮演着至关重要的角色,但是对于目标网站而言,频繁的爬虫请求可能会对其服务器产生不小的负担,严重的情况甚至会导致网站崩溃或者访问受限。为了避免这种情况的发生,同时也为了保护客户端…...

leetcode刷题笔记/代码随想录笔记——移除字符串中多余空格
1. 使用erase()函数 void removeExtraSpaces(string& s) {for (int i s.size() - 1; i > 0; i--) {if (s[i] s[i - 1] && s[i] ) {s.erase(s.begin() i);}}// 删除字符串最后面的空格if (s.size() > 0 && s[s.size() - 1] ) {s.erase(s.begi…...
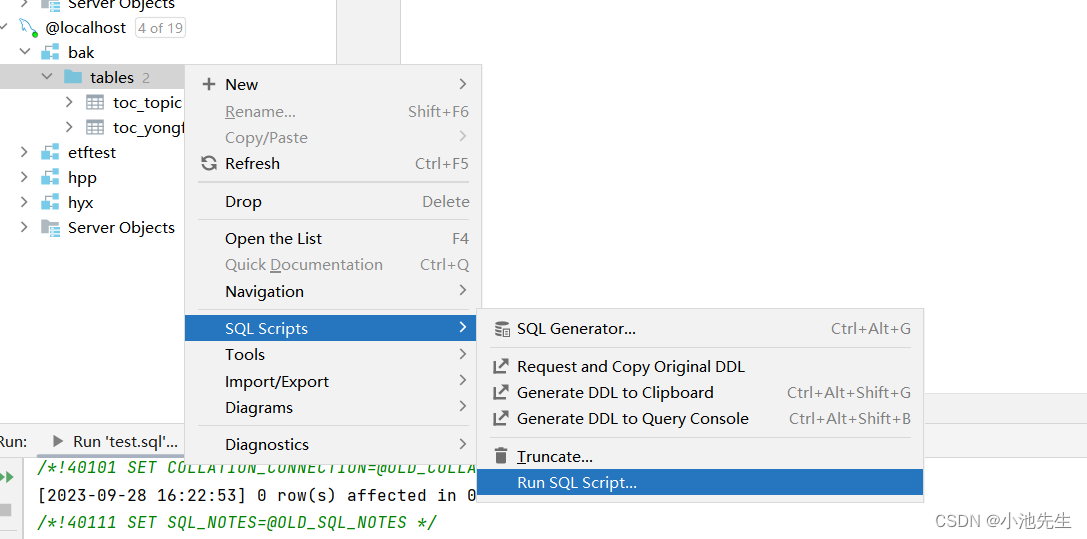
dataGrip导出导入的方式
导出:选中需要导出的表 导入:选中导出的sql文件...

LeetCode279. 完全平方数
279. 完全平方数 文章目录 [279. 完全平方数](https://leetcode.cn/problems/perfect-squares/)一、题目二、题解方法一:完全背包二维数组方法二:一维数组(空间复杂度更小的改进版本,最下面的两个版本不需要存储完全平方数) 一、题…...

【CMake】add_dependencies 命令
【CMake】add_dependencies 原文链接:https://blog.csdn.net/new9232/article/details/125831009 参考链接:https://blog.csdn.net/new9232/article/details/121374943 简介 add_dependencies(<target> [<target-dependency>]...)官方文档…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
