LeetCode279. 完全平方数
279. 完全平方数
文章目录
- [279. 完全平方数](https://leetcode.cn/problems/perfect-squares/)
- 一、题目
- 二、题解
- 方法一:完全背包二维数组
- 方法二:一维数组(空间复杂度更小的改进版本,最下面的两个版本不需要存储完全平方数)
一、题目
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
二、题解
方法一:完全背包二维数组
算法思路
这道题要求找到和为n的完全平方数的最少数量,下面是解题思路的详细说明:
-
首先,我们需要找到比n小的最大完全平方数,这个完全平方数不会大于n。我们可以通过遍历从1开始的完全平方数来找到这个数。在代码中,这部分的逻辑是:
int target = 0; int i = 1; for(i = 1; i <= n; i++){if(i * i > n){break;} } target = i - 1;这里的target就是比n小的最大完全平方数。
-
接下来,我们建立一个二维动态规划数组
dp,其中dp[i][j]表示使用前i个完全平方数,组成和为j的最少数量。 -
我们初始化
dp[1][i]为i,因为只能使用一个完全平方数1,所以组成任意数字j的最少数量都是j本身。 -
接下来,我们开始填充
dp数组的其余部分。我们从2号完全平方数开始,遍历完全平方数的个数(从2到target),然后遍历组成的和(从0到n)。在每个位置(i, j),我们有两个选项:- 保持
dp[i][j]不变,这意味着我们不使用当前的完全平方数i,所以最少数量与前一个状态dp[i-1][j]相同。 - 尝试使用当前的完全平方数i,如果可以的话,将
dp[i][j]更新为dp[i][j-i*i]+1,这表示使用了一个完全平方数i,所以数量加一。
- 保持
-
最终,
dp[target][n]就是答案,即使用前target个完全平方数组成和为n的最少数量。
具体实现
下面是具体的代码实现,已经按照上述思路注释:
class Solution {
public:int numSquares(int n) {// 寻找离n最接近的完全平方数int target = 0;int i = 1;for(i = 1; i <= n; i++){if(i * i > n){break;}}target = i - 1;// 建立dp数组,dp数组的含义是使用前i个完全平方数组成和为j的最少数量vector<vector<int>> dp(target+1, vector<int>(n+1, INT_MAX));// 初始化dp数组,使用一个完全平方数1,组成任意数字j的最少数量都是j本身for(int i = 0; i <= n; i++){dp[1][i] = i;}// 填充dp数组for(int i = 2; i <= target; i++){for(int j = 0; j <= n; j++){dp[i][j] = dp[i-1][j]; // 不使用当前完全平方数iif(j >= i * i && dp[i][j-i*i] != INT_MAX){dp[i][j] = min(dp[i][j], dp[i][j-i*i]+1); // 使用当前完全平方数i}}}return dp[target][n];}
};
算法分析
- 时间复杂度:遍历完全平方数1到target需要O(target)的时间,填充dp数组需要O(target * n)的时间。所以总时间复杂度是O(target * n)。
- 空间复杂度:使用了一个二维dp数组,大小为(target+1) * (n+1),所以空间复杂度是O(target * n)。
方法二:一维数组(空间复杂度更小的改进版本,最下面的两个版本不需要存储完全平方数)
class Solution {
public:int numSquares(int n) {// 建立dp数组,dp[i]表示凑成i所需要的最少完全平方数的个数vector<int> dp(n + 1, INT_MAX);dp[0] = 0;// 计算完全平方数列表vector<int> squares;for (int i = 1; i * i <= n; i++) {squares.push_back(i * i);}for (int i = 1; i <= n; i++) {for (int square : squares) {if (i < square) break; // 如果当前数小于完全平方数,则跳出循环dp[i] = min(dp[i], dp[i - square] + 1);}}return dp[n];}
};class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 0; i <= n; i++) { // 遍历背包for (int j = 1; j * j <= i; j++) { // 遍历物品dp[i] = min(dp[i - j * j] + 1, dp[i]);}}return dp[n];}
};
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 1; i * i <= n; i++) { // 遍历物品for (int j = i * i; j <= n; j++) { // 遍历背包dp[j] = min(dp[j - i * i] + 1, dp[j]);}}return dp[n];}
};
相关文章:

LeetCode279. 完全平方数
279. 完全平方数 文章目录 [279. 完全平方数](https://leetcode.cn/problems/perfect-squares/)一、题目二、题解方法一:完全背包二维数组方法二:一维数组(空间复杂度更小的改进版本,最下面的两个版本不需要存储完全平方数) 一、题…...

【CMake】add_dependencies 命令
【CMake】add_dependencies 原文链接:https://blog.csdn.net/new9232/article/details/125831009 参考链接:https://blog.csdn.net/new9232/article/details/121374943 简介 add_dependencies(<target> [<target-dependency>]...)官方文档…...

go语言unsafe.Pointer与uintptr
以下内容来源go语言圣经 1、unsafe.Pointer,相当于c语言中的void *类型的指针,如果需要运算需要转成uintptr类型的指针 2. uintptr uintptr是一个无符号的整型,它可以保存一个指针地址。 它可以进行指针运算。 uintptr无法持有对象, GC不把…...

ddos打到高防cdn上会发生什么
ddos打到cdn上会发生什么?当DDoS攻击打到CDN上时,肯定会影响网站的可用性和用户体验。具体DDoS攻击打到CDN上时,会发生以下情况: CDN节点负载增加:DDoS攻击会导致大量的无效流量涌入CDN节点,从而使得节点负载增加。这…...

【单调栈】503. 下一个更大元素 II
503. 下一个更大元素 II 解题思路 参考496. 下一个更大元素 I 首先计算nums2的每一个元素的下一个比他大的元素,使用单调栈 将上面的结果和nums2中的每一个元素组成映射map 针对每一个Nums1的元素 查询map 记录map 的value 但是这个是循环的数组元素 class So…...

C++ decltype类型
文章目录 1. 工作原理2. decltype 变量3. decltype 表达式4. decltype 函数 1. 工作原理 随着程序越来越复杂,程序中用到的类型也越来越多,我们有时候不得不去翻阅大量上下文去寻找此数据的类型。 decltype就是一种类型说明符,它的出现…...

【题解】JZOJ3854 分组
JZOJ 3854 题意 有 n n n 个人,每个人有地位 r i r_i ri 和年龄 a i a_i ai,对于一个若干人组成的小组,定义其队长为地位最高的成员(若相等则取二者均可),其他成员的年龄与队长的差不能超过 k k …...

区块链实验室(26) - 区块链期刊Blockchain: Research and Applications
Elsevier出版物“Blockchain: Research and Applications”是浙江大学编审的期刊。该期刊自2020年创刊,并出版第1卷。每年出版4期,最新期是第4卷第3期(2023年9月)。 目前没有官方的IF,Elsevier的引用因子Citescore是6.4。 虽然是新刊…...

【学习笔记】[ARC153F] Tri-Colored Paths
假设三种颜色的边都存在,并且不存在这样的路径 首先观察到,对于一个简单环上的边,颜色一定相同 因此,考虑建立圆方树,问题转化为圆方树上的 D P DP DP问题。限制是对于方点所连接的边,必须涂上相同的颜色…...
基于SSM的实习管理系统
基于SSM的实习管理系统、前后端分离 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 管理员界面 教师 学生 研究背景 基于SSM的实习管理系统是一个基于Spring、Spring…...
在Vue中通过ElementUI构建前端页面【登录,注册】,在IEDA构建后端实现前后端分离
一.ElementUI组件入门 1.对于ElementUI的理解 是一套基于 Vue.js 的开源UI组件库,提供了丰富的可复用组件,可以帮助开发者快速构建美观、易用的前端界面 2.Element UI 的特点和优势 多样化的组件:Element UI 提供了众多常用的基础组件&#…...

TX2 open ttyTHS2
TX2 open ttyTHS2 #冷风那个吹# 于 2019-04-01 14:10:43 发布 1749 收藏 6 分类专栏: 平时问题积累 TX2 版权 平时问题积累 同时被 2 个专栏收录 22 篇文章0 订阅 订阅专栏 TX2 30 篇文章8 订阅 订阅专栏 TX2上有5个串口,但是ttyTHS1是调试串口,ttyTHS3是蓝牙,ttyTHS…...

conan入门(二十八):解决conan 1.60.0下 arch64-linux-gnu交叉编译openssl/3.1.2报错问题
上一篇博客《conan入门(二十七):因profile [env]字段废弃导致的boost/1.81.0 在aarch64-linux-gnu下交叉编译失败》解决了conan 1.60.0交叉编译boost/1.80.1的问题后,我继续交叉编译openssl/3.1.2时又报错了 conan install openssl/3.1.2 -pr:h aarch64-linux-gnu.…...

Xcode 15 运行<iOS 14, 启动崩溃问题
如题. Xcode 15 启动 < iOS 14(没具体验证过, 我的问题设备是iOS 13.7)真机设备 出现启动崩溃 解决方案: Build Settings -> Other Linker Flags -> Add -> -ld64...
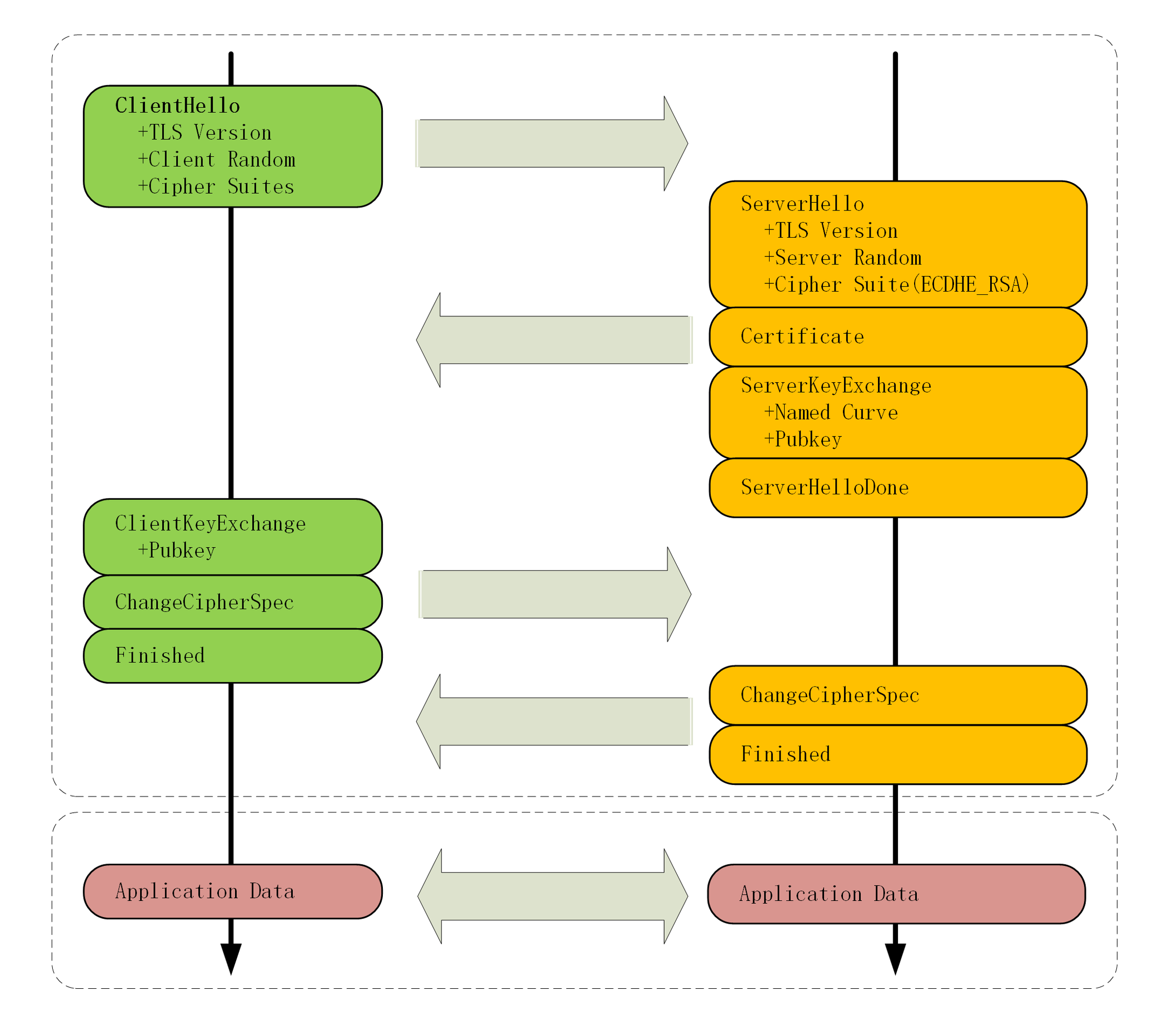
HTTPS协议概述
HTTPS(Hypertext Transfer Protocol over Secure Socket Layer,基于安全套接字层的超文本传输协议),是以安全为目标的HTTP通道,简单讲是HTTP的安全版。即HTTP下加入SSL层,HTTPS的安全基础是SSL,…...
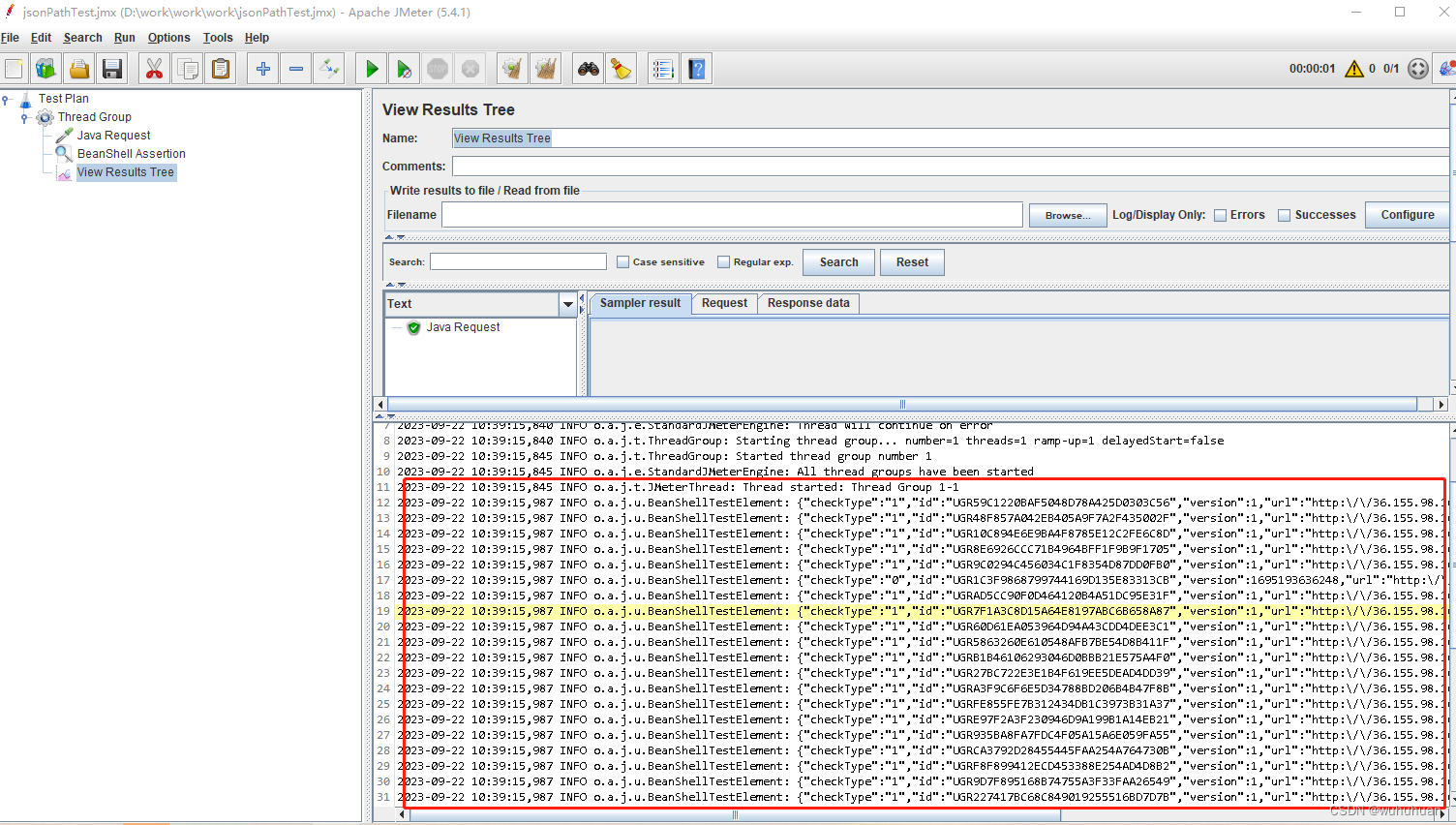
jmeterbeanshell调用jsonpath获取对应值
1.jmeter 新建线程组、Java Request、BeanShell Assertion、View Results Tree 2、在BeanShell Assertion中贴入代码: import org.apache.jmeter.extractor.json.jsonpath.JSONManager; import java.util.List; JSONManager js new JSONManager(); String jsonStr…...

C++中实现雪花算法来在秒级以及毫秒及时间内生成唯一id
1、雪花算法原理 雪花算法(Snowflake Algorithm)是一种用于生成唯一ID的算法,通常用于分布式系统中,以确保生成的ID在整个分布式系统中具有唯一性。它的名称来源于雪花的形状,因为生成的ID通常是64位的整数࿰…...
)
OPTEE Gprof(GNU profile)
安全之安全(security)博客目录导读 OPTEE调试技术汇总 目录 一、序言 二、Gprof使用 三、Gprof实现 1、Call graph information 2、PC distribution over time 一、序言 本文描述了如何使用gprof对TA进行概要分析。 配置选项CFG_TA_GPROF_SUPPORTy使OP-TEE能够从在用户模…...

MySQL 事务的操作指南(事务篇 二)
基本操作 事务的提交方式:自动提交(autocommit1)和手动提交(autocommit0) 查询和修改事务提交方式: -- 查看事务提交方式(标识表示这是个系统变量) select autocommit ;-- 修改事务提交方式为自动提交 …...

Oracle 查询 SQL 语句
目录 1. Oracle 查询 SQL 语句1.1. 性能查询常用 SQL1.1.1. 查询最慢的 SQL1.1.2. 列出使用频率最高的 5 个查询1.1.3. 消耗磁盘读取最多的 sql top51.1.4. 找出需要大量缓冲读取(逻辑读)操作的查询1.1.5. 查询每天执行慢的 SQL1.1.6. 从 V$SQLAREA 中查询最占用资源的查询1.1.…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术点解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术点解析 第一轮:基础概念问题 请解释Spring框架的核心容器是什么?它的作用是什么? 程序员JY回答:Spring框架的核心容器是IoC容器(控制反转…...
