【题解】JZOJ3854 分组
JZOJ 3854
题意
有 n n n 个人,每个人有地位 r i r_i ri 和年龄 a i a_i ai,对于一个若干人组成的小组,定义其队长为地位最高的成员(若相等则取二者均可),其他成员的年龄与队长的差不能超过 k k k。 q q q 次询问,若将 x , y x,y x,y 安排在同一个小组,那么这个小组最多多少人。
题解
先预处理每个人当队长时小组最多有多少人。设这个值为 c n t i cnt_i cnti。
具体来说,按 r r r 排序,对于 i i i 需要求前面 i i i 个人有多少个人的年龄在 [ a i − k , a i + k ] [a_i-k,a_i+k] [ai−k,ai+k] 的区间内。用一个动态开点权值线段树即可。下标是年龄。
考虑对询问离线。不妨假设 r x ≤ r y r_x\le r_y rx≤ry,那么对于一个询问 i i i,能够包含 x i , y i x_i,y_i xi,yi 的队长的范围是 r ≥ r y i , max ( a x i , a y i ) − k ≤ a ≤ min ( a x i , a y i ) + k r\ge r_{y_i},\max (a_{x_i},a_{y_i}) - k\le a\le \min(a_{x_i},a_{y_i})+k r≥ryi,max(axi,ayi)−k≤a≤min(axi,ayi)+k。因为与 x , y x,y x,y 的年龄差要同时小于 k k k,所以选范围小的区间。
按 r y r_y ry 为关键值将询问从大到小排序。然后一个动态开点权值线段树,下标是年龄,叶子节点存储 c n t i cnt_i cnti。这样对于一个询问,只需要查找在 [ max ( a x i , a y i ) − k , min ( a x i , a y i ) + k ] [\max (a_{x_i},a_{y_i}) - k,\min(a_{x_i},a_{y_i})+k] [max(axi,ayi)−k,min(axi,ayi)+k] 区间内的最大值即可。
时间复杂度 O ( n log w ) O(n\log w) O(nlogw)。
实现
记得判 -1。注意输入的标号是排序前的标号,要处理一下。
#include <bits/stdc++.h>
using namespace std;
const int N = 100005, W = 1e9;
int n, K, Q, ans[N], vp[N], cnt[N];
int tr[N << 4], mx[N << 4], rt1 = 0, rt2 = 0, tot1 = 0, tot2 = 0, ls1[N << 4], rs1[N << 4], ls2[N << 4], rs2[N << 4];
struct mem {int r, ag, id;bool operator< (const mem &T) const { return r < T.r; }
} a[N];
struct Query {int x, y, id;bool operator< (const Query &T) const { return a[y].r > a[T.y].r; }
} q[N];
void upd1(int &rt, int x, int y, int pos, int val) {if (!rt) rt = ++tot1;if (x == y) { tr[rt] += val; return; }int mid = x + y >> 1;if (pos <= mid) upd1(ls1[rt], x, mid, pos, val);else upd1(rs1[rt], mid + 1, y, pos, val);tr[rt] = tr[ls1[rt]] + tr[rs1[rt]];
}
int qry1(int rt, int x, int y, int l, int r) {if (l > y || r < x || !rt) return 0;if (l <= x && y <= r) return tr[rt];int mid = x + y >> 1;return qry1(ls1[rt], x, mid, l, r) + qry1(rs1[rt], mid + 1, y, l, r);
}
void upd2(int &rt, int x, int y, int pos, int val) {if (!rt) rt = ++tot2;if (x == y) { mx[rt] = max(mx[rt], val); return; }int mid = x + y >> 1;if (pos <= mid) upd2(ls2[rt], x, mid, pos, val);else upd2(rs2[rt], mid + 1, y, pos, val);mx[rt] = max(mx[ls2[rt]], mx[rs2[rt]]);
}
int qry2(int rt, int x, int y, int l, int r) {if (l > y || r < x || !rt) return 0;if (l <= x && y <= r) return mx[rt];int mid = x + y >> 1;return max(qry2(ls2[rt], x, mid, l, r), qry2(rs2[rt], mid + 1, y, l, r));
}
int main() {scanf("%d%d", &n, &K);for (int i = 1; i <= n; i++) scanf("%d", &a[i].r), a[i].id = i;for (int i = 1; i <= n; i++) scanf("%d", &a[i].ag);sort(a + 1, a + n + 1);for (int i = 1; i <= n; i++) vp[a[i].id] = i;for (int i = 1; i <= n; ) {int j = i;while (a[j].r == a[j + 1].r) upd1(rt1, 1, W, a[j].ag, 1), j++;upd1(rt1, 1, W, a[j].ag, 1);for (; i <= j; i++) cnt[i] = qry1(rt1, 1, W, a[i].ag - K, a[i].ag + K);}scanf("%d", &Q);for (int i = 1; i <= Q; i++) {scanf("%d%d", &q[i].x, &q[i].y), q[i].x = vp[q[i].x], q[i].y = vp[q[i].y], q[i].id = i;if (q[i].x > q[i].y) swap(q[i].x, q[i].y);}sort(q + 1, q + Q + 1);int k = n;for (int i = 1; i <= Q; i++) {while (q[i].y <= k) upd2(rt2, 1, W, a[k].ag, cnt[k]), k--;ans[q[i].id] = qry2(rt2, 1, W, max(a[q[i].x].ag, a[q[i].y].ag) - K, min(a[q[i].x].ag, a[q[i].y].ag) + K);if (ans[q[i].id] < 2) ans[q[i].id] = -1;}for (int i = 1; i <= Q; i++) printf("%d\n", ans[i]);return 0;
}
相关文章:

【题解】JZOJ3854 分组
JZOJ 3854 题意 有 n n n 个人,每个人有地位 r i r_i ri 和年龄 a i a_i ai,对于一个若干人组成的小组,定义其队长为地位最高的成员(若相等则取二者均可),其他成员的年龄与队长的差不能超过 k k …...

区块链实验室(26) - 区块链期刊Blockchain: Research and Applications
Elsevier出版物“Blockchain: Research and Applications”是浙江大学编审的期刊。该期刊自2020年创刊,并出版第1卷。每年出版4期,最新期是第4卷第3期(2023年9月)。 目前没有官方的IF,Elsevier的引用因子Citescore是6.4。 虽然是新刊…...

【学习笔记】[ARC153F] Tri-Colored Paths
假设三种颜色的边都存在,并且不存在这样的路径 首先观察到,对于一个简单环上的边,颜色一定相同 因此,考虑建立圆方树,问题转化为圆方树上的 D P DP DP问题。限制是对于方点所连接的边,必须涂上相同的颜色…...
基于SSM的实习管理系统
基于SSM的实习管理系统、前后端分离 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 管理员界面 教师 学生 研究背景 基于SSM的实习管理系统是一个基于Spring、Spring…...
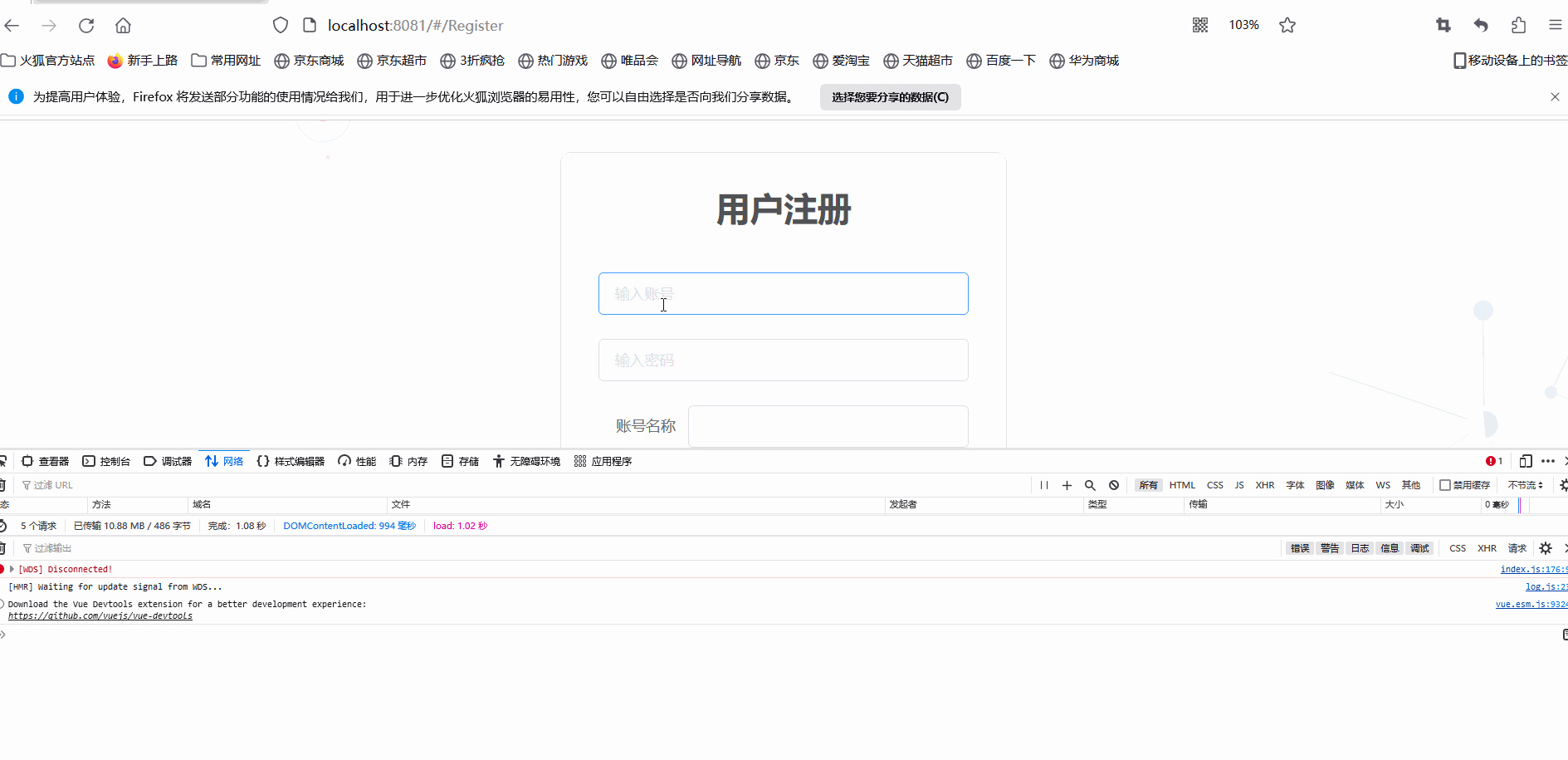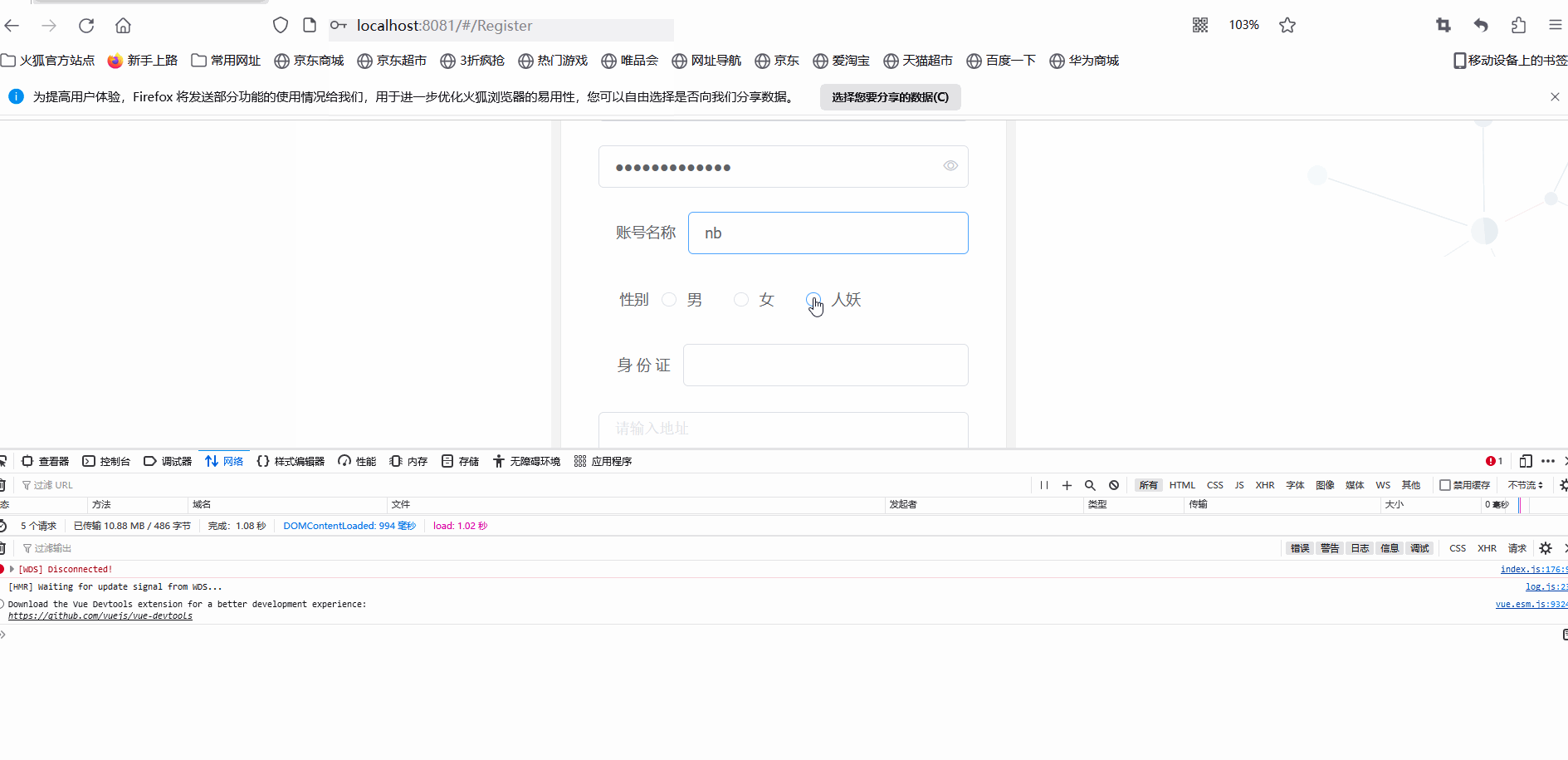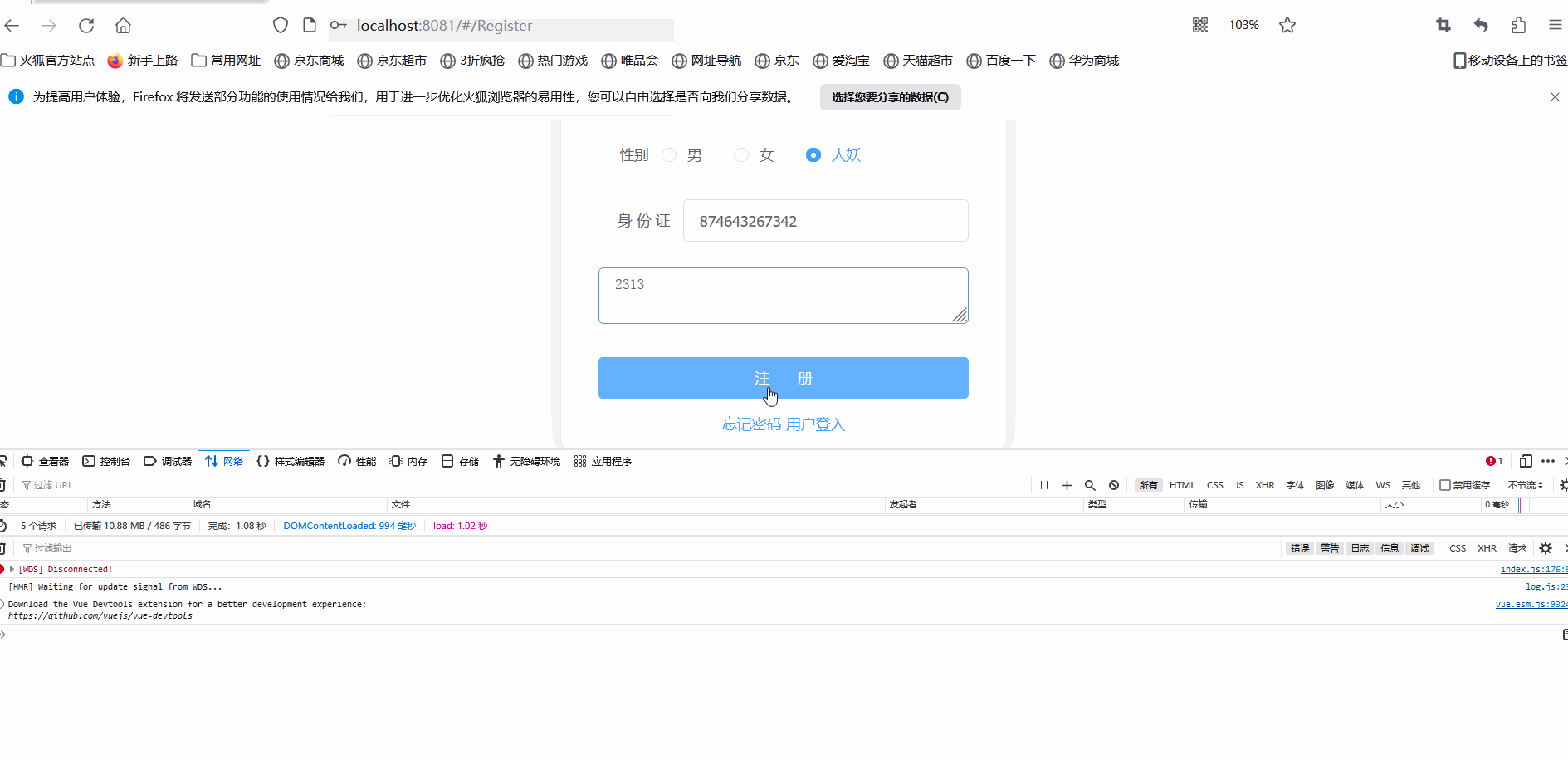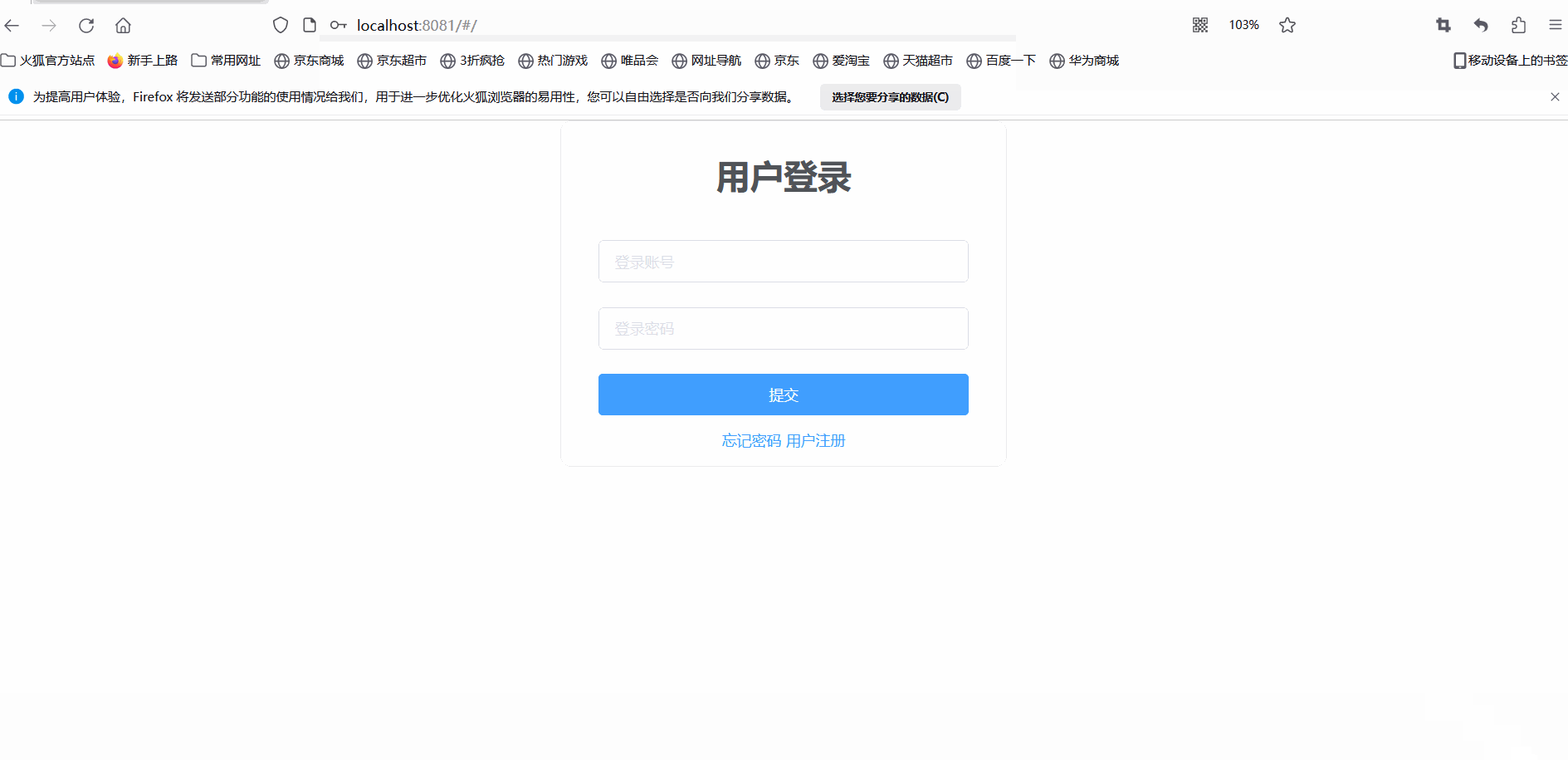
在Vue中通过ElementUI构建前端页面【登录,注册】,在IEDA构建后端实现前后端分离
一.ElementUI组件入门 1.对于ElementUI的理解 是一套基于 Vue.js 的开源UI组件库,提供了丰富的可复用组件,可以帮助开发者快速构建美观、易用的前端界面 2.Element UI 的特点和优势 多样化的组件:Element UI 提供了众多常用的基础组件&#…...

TX2 open ttyTHS2
TX2 open ttyTHS2 #冷风那个吹# 于 2019-04-01 14:10:43 发布 1749 收藏 6 分类专栏: 平时问题积累 TX2 版权 平时问题积累 同时被 2 个专栏收录 22 篇文章0 订阅 订阅专栏 TX2 30 篇文章8 订阅 订阅专栏 TX2上有5个串口,但是ttyTHS1是调试串口,ttyTHS3是蓝牙,ttyTHS…...

conan入门(二十八):解决conan 1.60.0下 arch64-linux-gnu交叉编译openssl/3.1.2报错问题
上一篇博客《conan入门(二十七):因profile [env]字段废弃导致的boost/1.81.0 在aarch64-linux-gnu下交叉编译失败》解决了conan 1.60.0交叉编译boost/1.80.1的问题后,我继续交叉编译openssl/3.1.2时又报错了 conan install openssl/3.1.2 -pr:h aarch64-linux-gnu.…...

Xcode 15 运行<iOS 14, 启动崩溃问题
如题. Xcode 15 启动 < iOS 14(没具体验证过, 我的问题设备是iOS 13.7)真机设备 出现启动崩溃 解决方案: Build Settings -> Other Linker Flags -> Add -> -ld64...
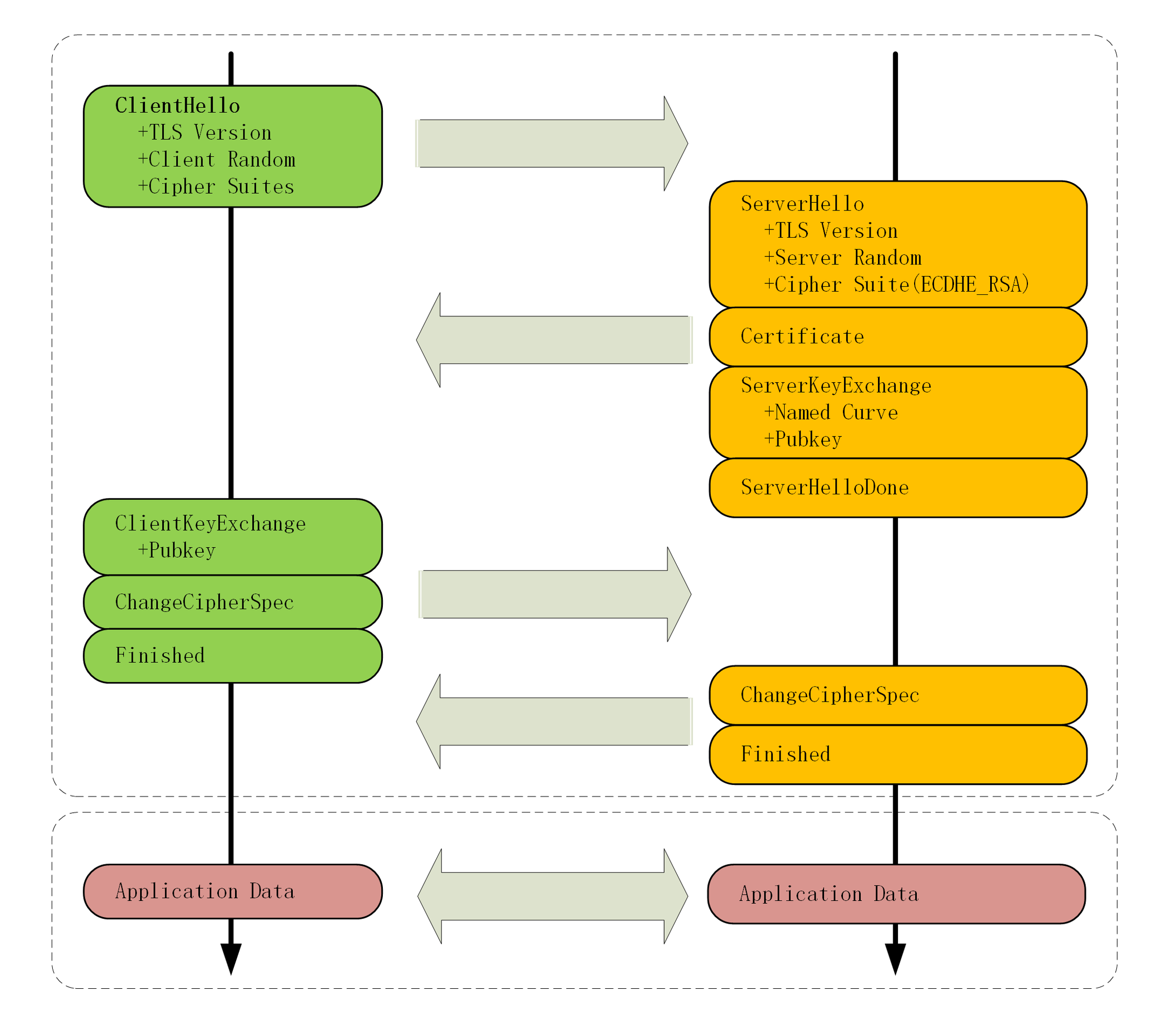
HTTPS协议概述
HTTPS(Hypertext Transfer Protocol over Secure Socket Layer,基于安全套接字层的超文本传输协议),是以安全为目标的HTTP通道,简单讲是HTTP的安全版。即HTTP下加入SSL层,HTTPS的安全基础是SSL,…...
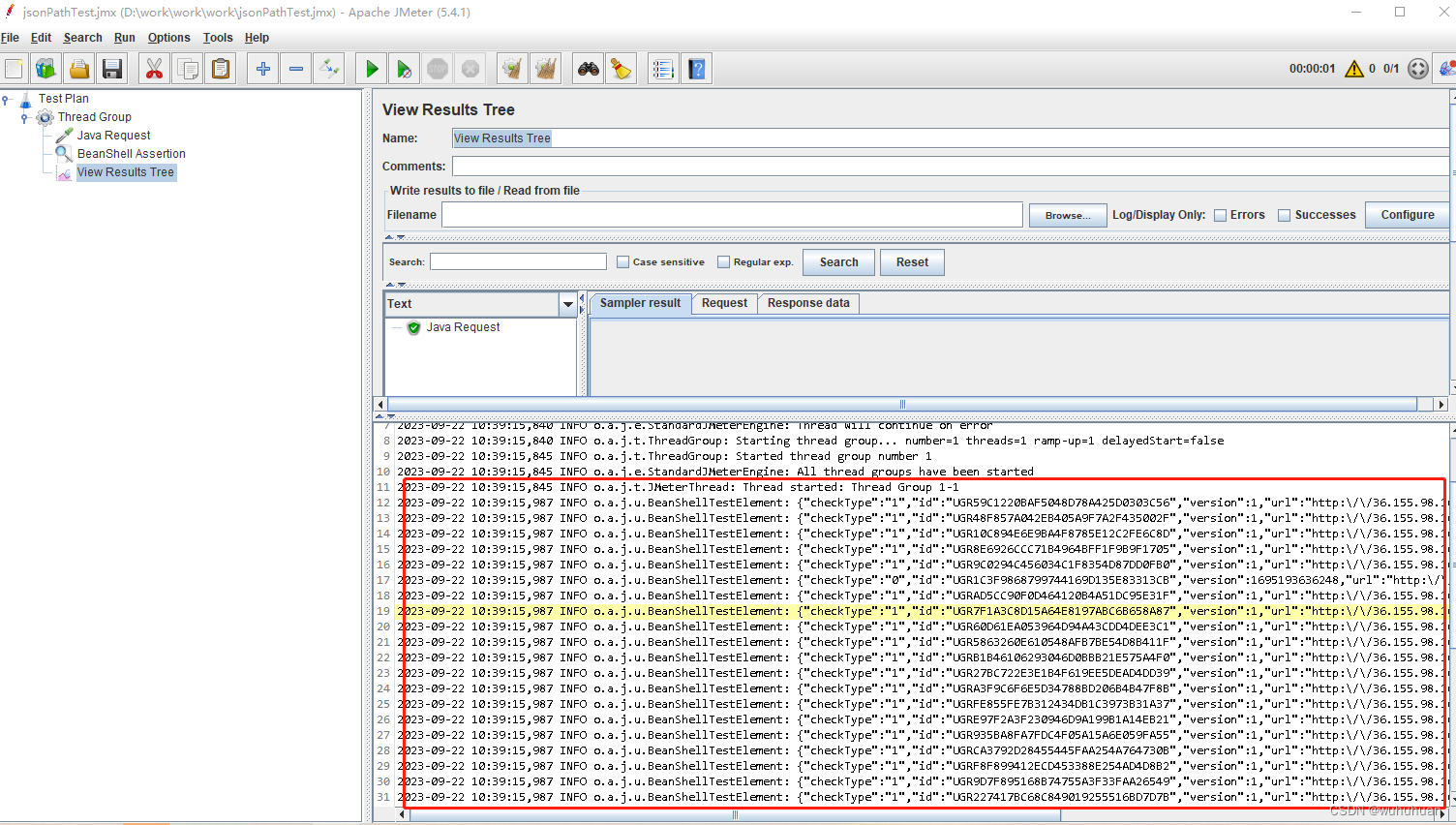
jmeterbeanshell调用jsonpath获取对应值
1.jmeter 新建线程组、Java Request、BeanShell Assertion、View Results Tree 2、在BeanShell Assertion中贴入代码: import org.apache.jmeter.extractor.json.jsonpath.JSONManager; import java.util.List; JSONManager js new JSONManager(); String jsonStr…...

C++中实现雪花算法来在秒级以及毫秒及时间内生成唯一id
1、雪花算法原理 雪花算法(Snowflake Algorithm)是一种用于生成唯一ID的算法,通常用于分布式系统中,以确保生成的ID在整个分布式系统中具有唯一性。它的名称来源于雪花的形状,因为生成的ID通常是64位的整数࿰…...
)
OPTEE Gprof(GNU profile)
安全之安全(security)博客目录导读 OPTEE调试技术汇总 目录 一、序言 二、Gprof使用 三、Gprof实现 1、Call graph information 2、PC distribution over time 一、序言 本文描述了如何使用gprof对TA进行概要分析。 配置选项CFG_TA_GPROF_SUPPORTy使OP-TEE能够从在用户模…...

MySQL 事务的操作指南(事务篇 二)
基本操作 事务的提交方式:自动提交(autocommit1)和手动提交(autocommit0) 查询和修改事务提交方式: -- 查看事务提交方式(标识表示这是个系统变量) select autocommit ;-- 修改事务提交方式为自动提交 …...

Oracle 查询 SQL 语句
目录 1. Oracle 查询 SQL 语句1.1. 性能查询常用 SQL1.1.1. 查询最慢的 SQL1.1.2. 列出使用频率最高的 5 个查询1.1.3. 消耗磁盘读取最多的 sql top51.1.4. 找出需要大量缓冲读取(逻辑读)操作的查询1.1.5. 查询每天执行慢的 SQL1.1.6. 从 V$SQLAREA 中查询最占用资源的查询1.1.…...

gin 基本使用
gin 初体验 import ("net/http""github.com/gin-gonic/gin" )func main() {r : gin.Default()r.GET("/ping", func(c *gin.Context) {c.JSON(http.StatusOK, gin.H{"message": "pong",})})r.Run() }gin 路由接受一个 type …...
8月最新修正版风车IM即时聊天通讯源码+搭建教程
8月最新修正版风车IM即时聊天通讯源码搭建教程。风车 IM没啥好说的很多人在找,IM的天花板了,知道的在找的都知道它的价值,开版好像就要29999,后端加密已解,可自己再加密,可反编译出后端项目源码,已增加启动后端需要google auth双重验证,pc端 web端 wap端 android端 ios端 都有 …...

NSDT孪生场景编辑器系统介绍
一、产品背景 数字孪生的建设流程涉及建模、美术、程序、仿真等多种人才的协同作业,人力要求高,实施成本高,建设周期长。如何让小型团队甚至一个人就可以完成数字孪生的开发,是数字孪生工具链要解决的重要问题。考虑到数字孪生复杂…...
3D WEB轻量化引擎HOOPS助力3D测量应用蓬勃发展:效率、精度显著提升
在3D开发工具领域,Tech Soft 3D打造的HOOPS SDK已经崭露头角,成为了全球领先的3D领域开发工具提供商。HOOPS SDK包括四种不同的3D软件开发工具,已成为行业的翘楚。 其中,HOOPS Exchange以其CAD数据转换的能力脱颖而出,…...

【Orange Pi】Orange Pi5 Plus 安装记录
官网:Orange Pi - Orangepi 主控芯片:Rockchip RK3588(8nm LP制程)NPU:内嵌的 NPU 支持INT4/INT8/INT16/FP16混合运算,算力高达 6Top支持的操作系统: Orangepi OS(Droid)Orangepi O…...

NLP 项目:维基百科文章爬虫和分类 - 语料库阅读器
塞巴斯蒂安 一、说明 自然语言处理是机器学习和人工智能的一个迷人领域。这篇博客文章启动了一个具体的 NLP 项目,涉及使用维基百科文章进行聚类、分类和知识提取。灵感和一般方法源自《Applied Text Analysis with Python》一书。 在接下来的文章中,我将…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
