216. 组合总和 III
找出所有相加之和为
n的k个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7 输出: [[1,2,4]] 解释: 1 + 2 + 4 = 7 没有其他符合的组合了。示例 2:
输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]] 解释: 1 + 2 + 6 = 9 1 + 3 + 5 = 9 2 + 3 + 4 = 9 没有其他符合的组合了。示例 3:
输入: k = 4, n = 1 输出: [] 解释: 不存在有效的组合。 在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。提示:
2 <= k <= 91 <= n <= 60
class Solution {
public:vector<int> path;vector<vector<int>> res;int sum=0;void func(int k,int n,int index){if(sum>n)return;if(path.size()==k){if(sum==n)res.push_back(path);return;}for(int i=index;i<=9;i++){sum+=i;path.push_back(i);func(k,n,i+1);path.pop_back();sum-=i;}}vector<vector<int>> combinationSum3(int k, int n) {func(k,n,1);return res;}
};相关文章:

216. 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件: 只使用数字1到9每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。 示例 1: 输入: k 3, n 7 输出: [[1,2,4]] 解释: …...
(136))
【Java】数组的深浅拷贝问题(二维数组举例)(136)
深拷贝和浅拷贝: 对于数组来说,深拷贝就是相当于拷贝了数组的对象(基本数据类型),也就是数组当中的内容。而浅拷贝就是拷贝的是数组的地址(引用类型),浅拷贝只是复制了对象的引用地…...

【轮趣-科大讯飞】M260C 环形六麦测试 2 - ROS1功能测试与唤醒、语音识别程序解析
所有内容请看: 博客学习目录_Howe_xixi的博客-CSDN博客https://blog.csdn.net/weixin_44362628/article/details/126020573?spm1001.2014.3001.5502原文在飞书,请联系我获取阅读链接,我太懒了...

油猴(篡改猴)学习记录
第一个Hello World 注意点:默认只匹配了http网站,如果需要https网站,需要自己添加match https://*/*代码如下 这样子访问任意网站就可以输出Hello World // UserScript // name 第一个脚本 // namespace http://tampermonkey.net/ // version 0.1 // descri…...

LeetCode 面试题 05.08. 绘制直线
文章目录 一、题目二、Java 题解 一、题目 已知一个由像素点组成的单色屏幕,每行均有 w 个像素点,所有像素点初始为 0,左上角位置为 (0,0)。 现将每行的像素点按照「每 32 个像素点」为一组存放在一个 int 中,再依次存入长度为 le…...
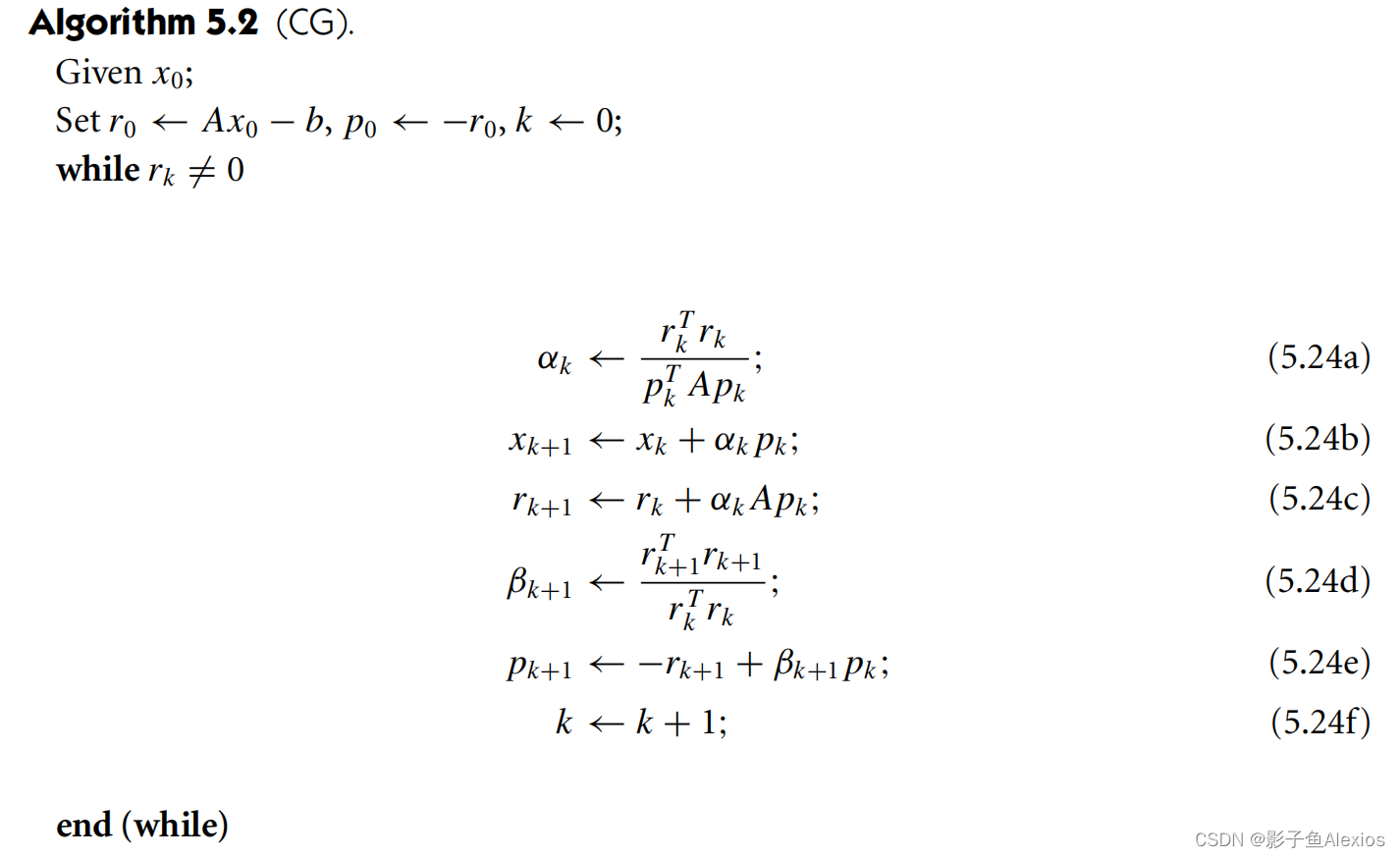
机器人中的数值优化|【六】线性共轭梯度法,牛顿共轭梯度法
机器人中的数值优化|【六】线性共轭梯度法,牛顿共轭梯度法 往期回顾 机器人中的数值优化|【一】数值优化基础 机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例 机器人中的数值优化|【三】无约束优化…...
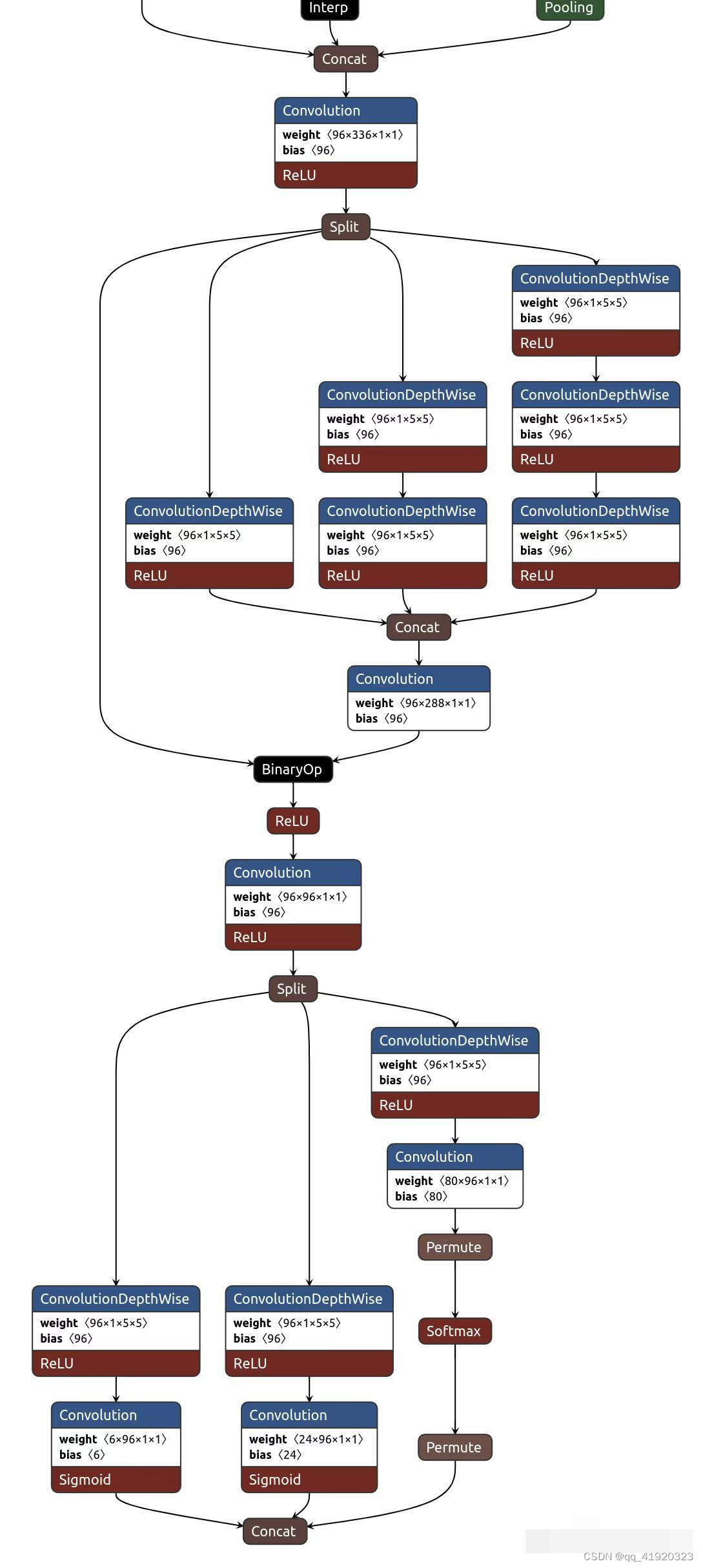
FastestDet---原理介绍
1.测试指标 2.算法定位 FastestDet是设计用来接替yolo-fastest系列算法,相比于业界已有的轻量级目标检测算法如yolov5n, yolox-nano, nanoDet, pp-yolo-tiny, FastestDet和这些算法根本不是一个量级,FastestDet无论在速度还是参数量上,都是要小好几个数量级的,但是精度自然…...
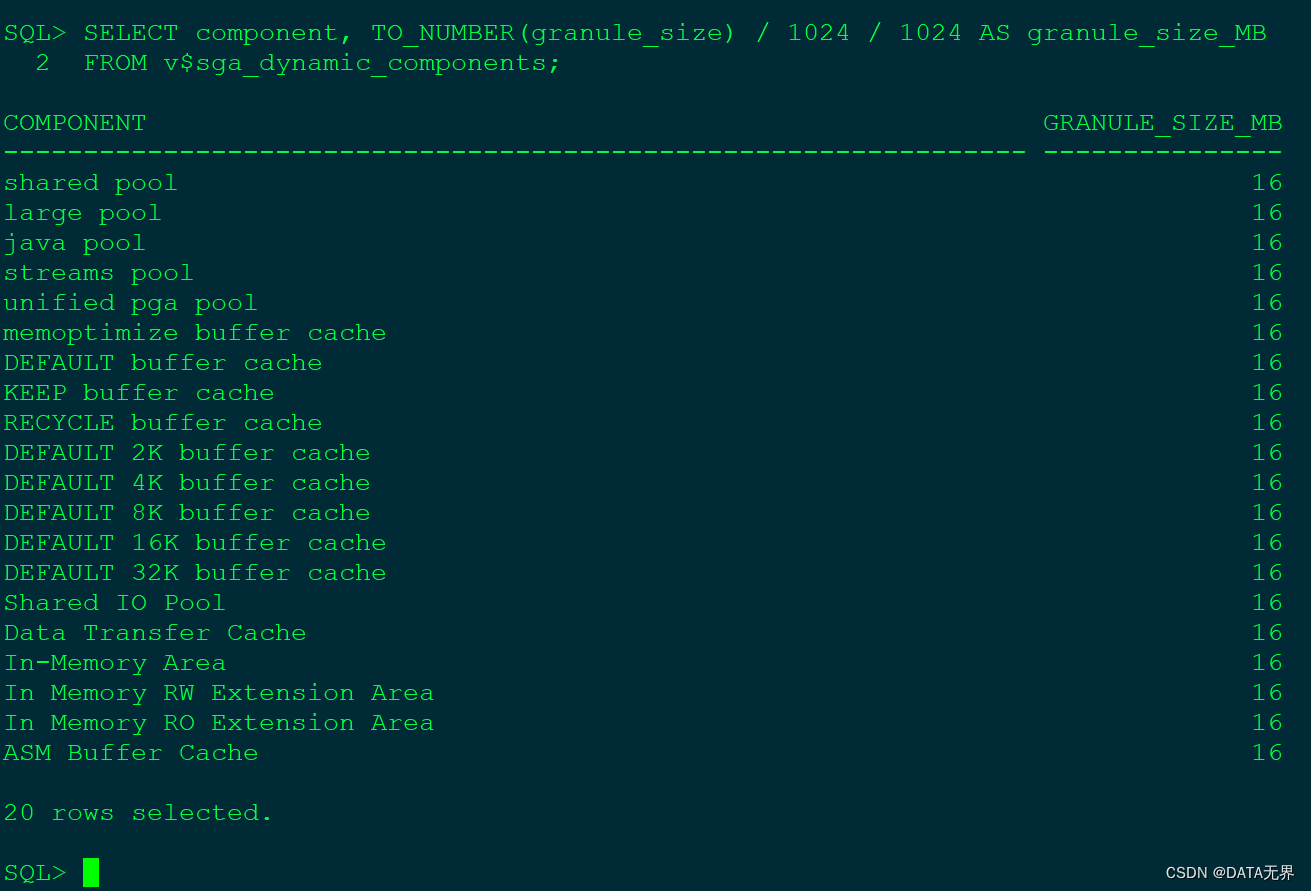
ORACLE 在内存管理机制上的演变和进化
截止目前,计算机内存仍然被认为是我们可以获得的最快速度的物理存储设备。 将频繁访问的数据尽可能地置于内存中,已成为当前各种软件和应用程序提高数据访问性能,减少访问延迟的最为有效的途径。 然而,内存作为关键的计算资源&am…...
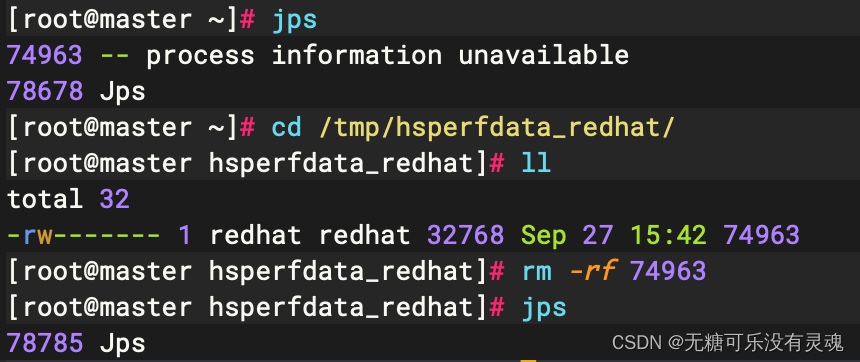
Linux ❀ 进程出现process information unavailable时的消除方法
[rootmaster ~]# jps 74963 -- process information unavailable 78678 Jps [rootmaster ~]# cd /tmp/hsperfdata_redhat/ # redhat为启动该java进程的用户ps -ef | grep $pid查找 [rootmaster hsperfdata_redhat]# ll total 32 -rw------- 1 redhat redhat 32768 Sep 27 15:…...
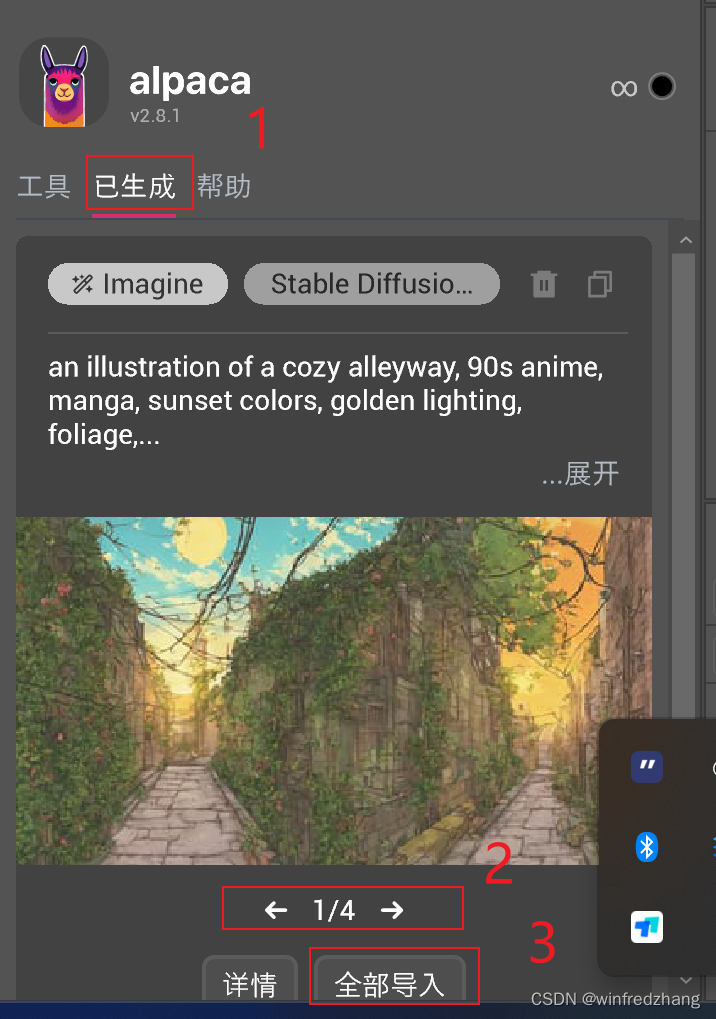
ps智能填充功能平替:alpaca的安装和使用
为了解决ps beta 智能填充无法使用的问题,需要用alpaca来平替,下面是安装教程: 安装方法: 1、下载插件。 alpaca插件汉化-夸克网盘https://pan.quark.cn/s/1168b447a44e#/list/share 2、 根据使用的PS版本,选择对应文件…...

【前端打怪升级日志之ES6篇】玩转函数
学习资料 阮一峰老师《ECMAScript 6 入门》— 函数的扩展 总结应用 1. 函数参数默认值与对象解构赋值默认值的结合使用 // 场景:方法调用时传参希望只传第二个参数 // 方案1: function foo({x1,y2}){console.log(x,y); } foo({}) //1 2 foo({x:2}) /…...
网址静态码手机制作教程,附图文详解!
网址的静态码是如何生成的呢?静态码是二维码的一种常用类型,一般常见的静态码类型主要是文本或者网址,那么在电脑制作静态码的方法相信很多小伙伴都知道怎么做,那么手机上制作的方法,大家感兴趣吗?下面来给…...
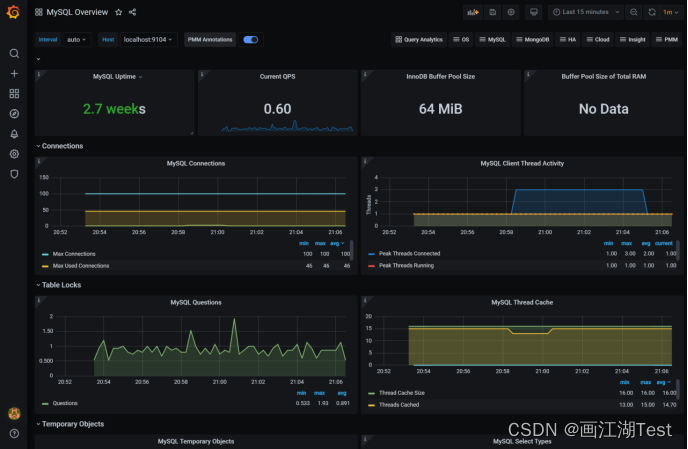
服务器性能测试监控平台export+prometheus(普罗米修斯)+grafana搭建
1. export 数据采集工具 简介: export是prometheus是的数据采集组件的总称,它可以将采集到的数据转为prometheus支持的格式 node_export: 用来监控服务器硬件资源的采集器,端口号为9100mysql_export: 用来监控mysql数据库资源的采集器&…...

【24种设计模式】责任链模式
责任链模式是一种行为设计模式,它允许你将请求沿着处理链进行传递,直到有一个处理者能够处理该请求为止。这种模式将请求的发送者和接收者解耦,使多个对象都有机会处理该请求。 责任链模式的结构 责任链模式由以下几个角色组成:…...

C#异步委托的三种实现 BeginInvoke / EndInvoke / IsCompleted
本文将介绍C#异步委托的三种实现方式,并给出相关示例代码及解析。 注意事项 用委托开启线程的前提是:创建项目时必须选择“.NET Framework",如果选择的是”.Net Core“,在调用BeginInvoke时,系统会报错”Operati…...

在HTTP请求中安全传输base64编码的字符串
前言 base64是一种常见的的编码格式,它可以把二进制数据编码成一个由大小写英文字母(a-zA-Z)、阿拉伯数字(0-9),以及三个特殊字符、/、组成的字符串。 问题 但是在URL传输中,、/、这三个特殊…...

05预测识别-依托YOLO V8进行训练模型的识别——对视频中的图片进行识别
在前面的一些章节中,我们已经讲如何准备打标签的素材、如何制作标签、如何训练以及得到我们最终需要的用于YOLO目标识别的模型。那么现在我们就要正式开始,利用我们训练得到的best.pt,这个模型文件来对图片视频进行识别。 1、基本思路 公安交管场景中,我们经常会遇到需要…...
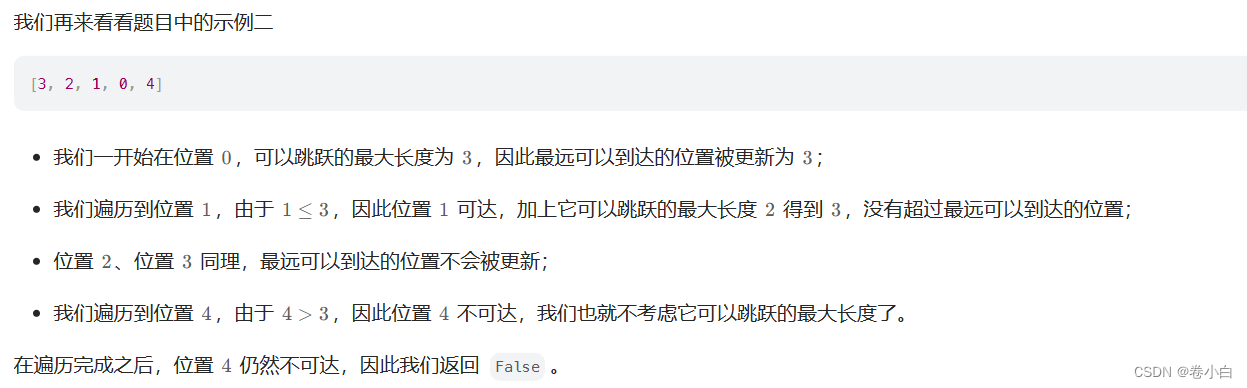
LeetCode算法题---第3天
注:大佬解答来自LeetCode官方题解 121.买卖股票的最佳时期 1.题目 2.个人解答 function maxProfit(prices) {//更新最低价格和最大利润let minPrice prices[0];let maxProfit 0;for (let i 1; i < prices.length; i) {// 如果当前价格比最低价格还低,更新最…...

欧洲FBA专线海运与陆运的差别
随着全球电商市场的快速发展,越来越多的卖家选择将产品销售到欧洲市场。然而,面对欧洲境内的物流问题,卖家们往往会面临一个重要的选择:选择欧洲FBA专线时是选择海运还是陆运?这两种运输方式在时效、成本和服务质量上都有所不同&…...
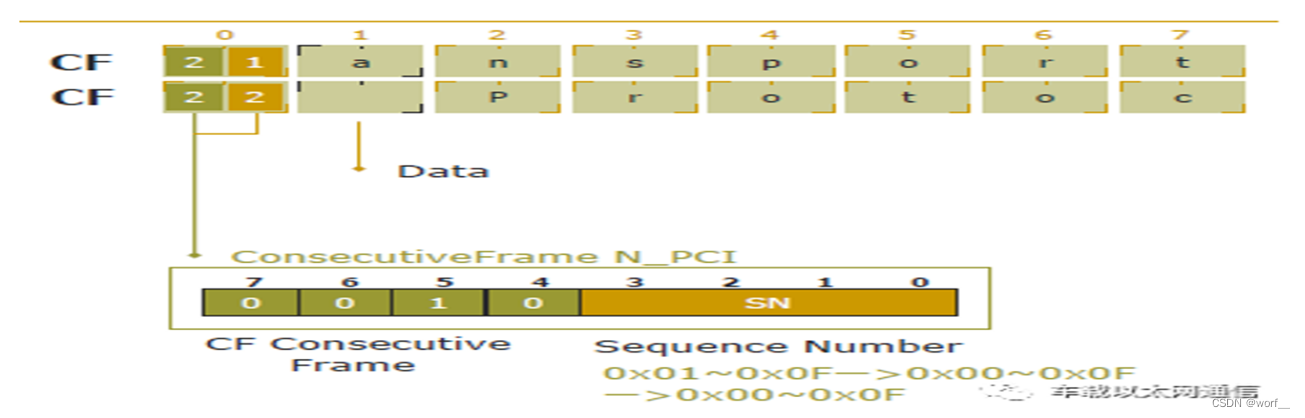
UDS诊断
一、UDS诊断简介 汽车诊断技术是指在不拆卸车辆的情况下,通过读取车辆在运行过程中所记录的数据或故障码来查明故障原因,并确定故障部位的汽车应用技术。通过诊断,可以快速检测到汽车故障来提高汽车安全性和维修效率。 USD协议诊断主要采用“…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
