数据结构初阶——时间复杂度与空间复杂度
时间复杂度与空间复杂度
- 1. 算法效率
- 1.1 如何衡量一个算法的好坏
- 1.2算法的复杂度
- 2.时间复杂度
- 2.1 时间复杂度的概念
- 2.2 大O的渐进表示法
- 2.3常见时间复杂度计算举例
- 实列1:
- 实列2:
- 实列3:
- 实列4:
- 实列5:
- 实列6:
- 实列7:
- 实列8:
- 3.空间复杂度
- 实例1:
- 实例2:
- 实例3:
- 实例4:
- 4. 常见复杂度对比
1. 算法效率
1.1 如何衡量一个算法的好坏
如何衡量一个算法的好坏呢?比如对于以下斐波那契数列
long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
1.2算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。
在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
2.时间复杂度
2.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度
请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
执行次数

实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
2.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为O(N^2)
- N = 10 F(N) = 100
- N = 100 F(N) = 10000
- N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.3常见时间复杂度计算举例
实列1:
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
时间复杂度为:O(N)
当N足够大时N与2N可视为相同,所以时间复杂度为O(N)
只要是,常数 * N 时间复杂度都是O(N)
实列2:
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}
时间复杂度为:O(M+N)
当M与N的值不确定的时候时间复杂度就为O(M+N)
如果有提示M远大于N,或者N远大于M,时间复杂度为O(N)或者O(M)
实列3:
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
时间复杂度为:O(1)
只要是常数,时间复杂度都为O(1)
实列4:
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );
vs中strchr函数的实现如下

返回指向 string 中第一个出现的字符的指针。
如果未找到该字符,则该函数将返回一个空指针。
假设string指向字符串“abvdefg”
如果我们找a一次就可以找到
如果找d第四次就可以找到
如果我们要找的字符没有出现在字符串中,那我们就可能会找N次
上面我们有讲到,在实际中一般情况关注的是算法的最坏运行情况,所以这道题的时间复杂度为O(N)
实列5:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
时间复杂度为:O(N^2)


实列6:
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin < end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid;elsereturn mid;}return -1;
}
这是一个典型的二分查找
时间复杂度为:O(logN)
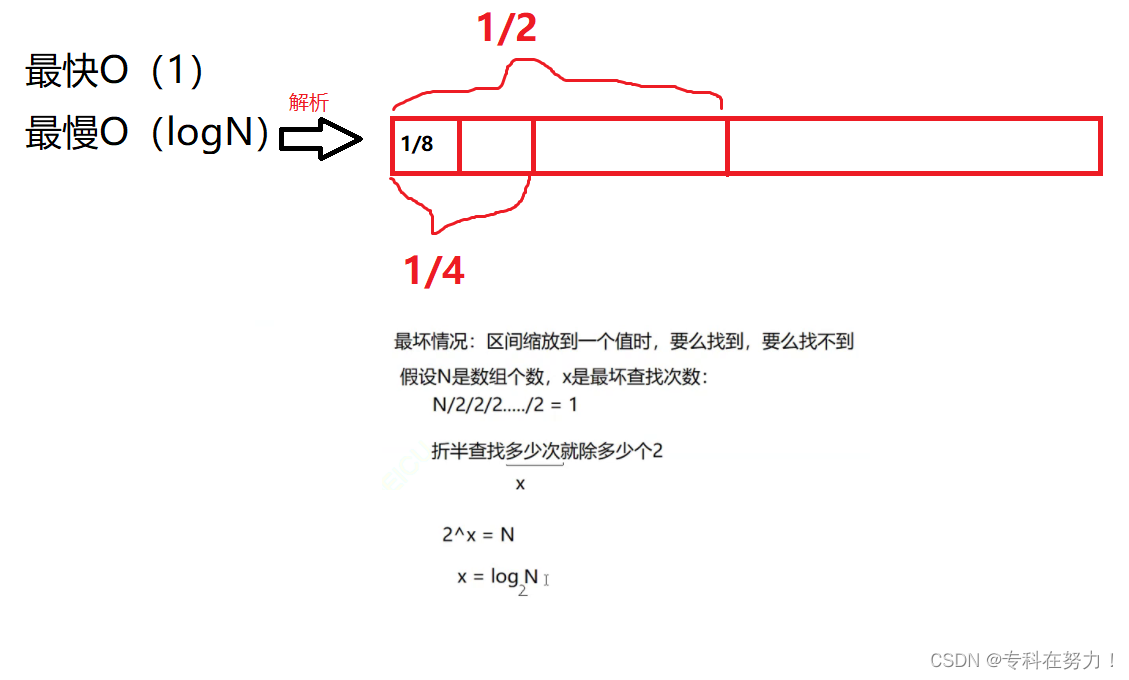
实列7:
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
时间复杂度为:O(N)
实列8:
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
时间复杂度为:O(2^N)
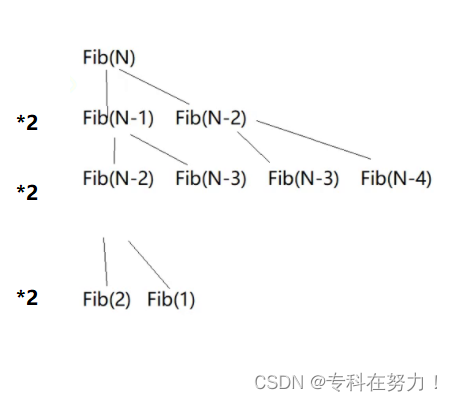
这段代码看着简短,实际运行起来很浪费时间,所以实际中不建议使用
3.空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
实例1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
使用了常数个额外空间,所以空间复杂度为 O(1)
实例2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}
动态开辟了N个空间,空间复杂度为 O(N)
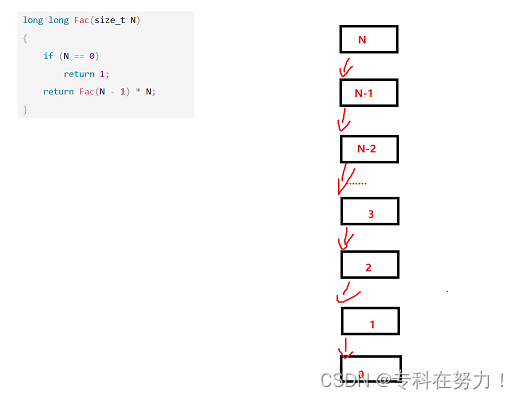
实例3:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
实例4:
// 计算斐波那契递归Fib的空间复杂度?
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}

4. 常见复杂度对比
一般算法常见的复杂度如下:
相关文章:

数据结构初阶——时间复杂度与空间复杂度
时间复杂度与空间复杂度1. 算法效率1.1 如何衡量一个算法的好坏1.2算法的复杂度2.时间复杂度2.1 时间复杂度的概念2.2 大O的渐进表示法2.3常见时间复杂度计算举例实列1:实列2:实列3:实列4:实列5:实列6:实列…...

深度学习之“制作自定义数据”--torch.utils.data.DataLoader重写构造方法。
深度学习之“制作自定义数据”–torch.utils.data.DataLoader重写构造方法。 前言: 本文讲述重写torch.utils.data.DataLoader类的构造方法,对自定义图片制作类似MNIST数据集格式(image, label),用于自己的Pytorc…...
#G. 求约数个数之六
我们先求到区间[1..b]之间的所有约数之和于是结果就等于 [1..b]之间的所有约数之和减去[1..a-1]之间的约数之和很明显这两个问题是同性质的问题,只是右端点不同罢了.明显对于1到N之间的数字,其约数范围也为1到N这个范围内。于是我们可以枚举约数L,当然这…...

如何为Java文件代码签名及添加时间戳?
Java是一种流行的编程语言,大多数组织都使用它来开发业务应用程序。由于其高使用率,攻击者总是试图找到其中的漏洞并基于它利用软件。为了防止此类攻击, 为 Java 文件(.jar)进行代码签名并添加时间戳,可以防…...

Xamarin.Forsm for Android 显示 PDF
背景 某些情况下,需要让用户阅读下发的文件,特别是红头文件,这些文件一般都是使用PDF格式下发,这种文件有很重要的一点就是不能更改。这时候就需要使用原文件进行展示。 Xamarin.Forms Android 中的 WebView 控件是不能直接显示的…...

RK3399平台开发系列讲解(LED子系统篇)LED子系统详解
🚀返回专栏总目录 文章目录 一、设备树编写二、LED子系统2.1、用户态2.2、内核驱动三、驱动代码3.1、平台设备驱动的注册3.2、平台设备驱动的probe四、使用方法沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇将详细介绍LED子系统。 一、设备树编写 节点属性添加…...
 的数据结构)
LeetCode 432. 全 O(1) 的数据结构
LeetCode 432. 全 O(1) 的数据结构 难度:hard\color{red}{hard}hard 题目描述 请你设计一个用于存储字符串计数的数据结构,并能够返回计数最小和最大的字符串。 实现 AllOneAllOneAllOne 类: AllOne()AllOne()AllOne() 初始化数据结构的对…...
再析jvm
前言 希望自己每一次学习都有不同的理解 文章目录前言1. jvm的组成取消永久代使用元空间原因2. 运行时数据区3. 堆栈区别队列和栈,队列先进先出,栈先进后出从栈顶弹出4. GC、内存溢出、垃圾回收4.1 如何确定引用是否会被回收4.1.1 Java中的引用类型4.1.…...

社招前端二面面试题总结
代码输出结果 var A {n: 4399}; var B function(){this.n 9999}; var C function(){var n 8888}; B.prototype A; C.prototype A; var b new B(); var c new C(); A.n console.log(b.n); console.log(c.n);输出结果:9999 4400 解析: conso…...
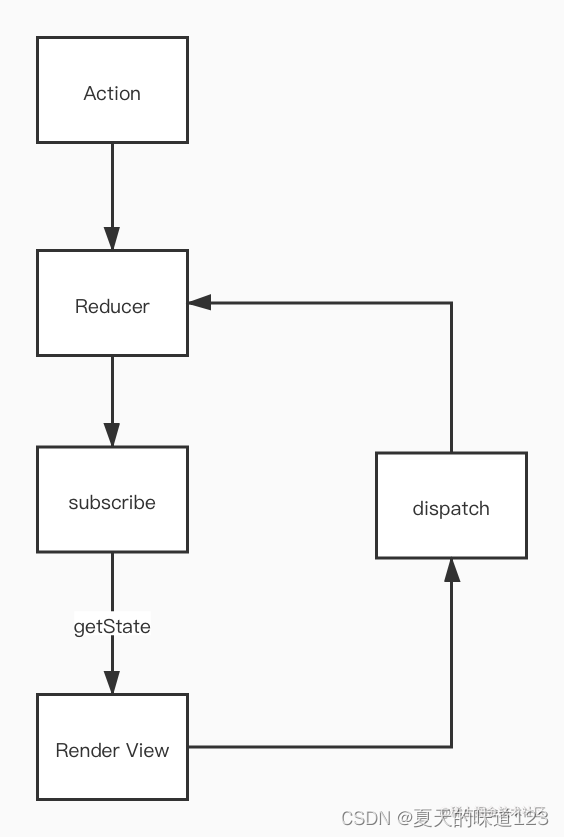
人人能读懂redux原理剖析
一、Redux是什么? 众所周知,Redux最早运用于React框架中,是一个全局状态管理器。Redux解决了在开发过程中数据无限层层传递而引发的一系列问题,因此我们有必要来了解一下Redux到底是如何实现的? 二、Redux的核心思想…...
uniCloud云开发----7、uniapp通过uni-swiper-dot实现轮播图
uniapp通过uni-swiper-dot实现轮播图前言效果图1、官网实现的效果2、需求中使用到的效果图官网提供的效果图源码1、html部分2、js部分3、css部分根据需求调整轮播图前言 uni-swiper-dot.文档 uni-swiper-dot 轮播图指示点 - DCloud 插件市场 本次展示根据需求制作的和官网用到…...

IM即时通讯构建企业协同生态链
在当今互联网信息飞速发展的时代,随着企业对协同办公要求的提高,协同办公的定义提升到了智能化办公的范畴。大多企业都非常重视构建连接用户、员工和合作伙伴的生态平台,利用即时通讯软件解决企业内部的工作沟通、信息传递和知识共享等问题。…...

Python实现构建gan模型, 输入一个矩阵和两个参数值,输出一个矩阵
构建一个GAN模型,使用Python实现,该模型将接受一个矩阵和两个参数值作为输入,并输出另一个矩阵。GAN(生成对抗网络)是一种深度学习模型,由生成器和判别器两部分组成,可以用于生成具有一定规律性的数据,如图像或音频。 # 定义生成器 def make_generator(noise_dim, dat…...
开学准备哪些电容笔?ipad触控笔推荐平价
在现代,数码产品的发展受到高技术的驱动。不管是在工作上,还是在学习上,大的显示屏可以使图像更加清晰。Ipad将成为我们日常生活中不可或缺的一部分,无论现在或将来。如果ipad配上一款方便操作的电容笔,将极大地提高我…...

放下和拿起 解放自己
放下太难,从过去中解放自己 工作这么久了,第一次不拿包上班,真爽 人的成长都是在碰撞和摸索中产生的,通过摸索,知道自己能力的边界和欲望的边界以及身体的边界,这三个决定了 你能做什么 你能享受什么&…...

100%BIM学员的疑惑:不会CAD可以学Revit吗?
在新一轮科技创新和产业变革中,信息化与建筑业的融合发展已成为建筑业发展的方向,将对建筑业发展带来战略性和全局性的影响。 建筑业是传统产业,推动建筑业科技创新,加快推进信息化发展,激发创新活力,培育…...

经常会采坑的javascript原型应试题
一. 前言 原型和原型链在面试中历来备受重视,经常被提及。说难可能也不太难,但要真正完全理解,吃透它,还是要多下功夫的。 下面为大家简单阐述我对原型和原型链的理解,若是觉得有说的不对的地方ÿ…...

完全背包—动态规划
一、背包问题概述 如图,完全背包与01背包的区别只有一点:01背包中每个物品只能取一个而完全背包中每个物品可以取无数个。解决完全背包问题必须首先弄明白01背包,不清楚的可以看我的这篇文章01背包—动态规划。 二、例题 重量价值物品0115物…...

消息队列MQ介绍
消息队列技术是分布式应用间交换信息的一种技术。消息队列可驻留在内存或磁盘上,队列存储消息直到它们被应用程序读走。通过消息队列,应用程序可独立地执行--它们不需要知道彼此的位置、或在继续执行前不需要等待接收程序接收此消息。 消息中间件概述 消息队列技术是…...

C语言进阶(八)—— 链表
1. 链表基本概念1.1 什么是链表链表是一种常用的数据结构,它通过指针将一些列数据结点,连接成一个数据链。相对于数组,链表具有更好的动态性(非顺序存储)。数据域用来存储数据,指针域用于建立与下一个结点的…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...
