JavaScript位运算的妙用
位运算的妙用: 奇偶数, 色值换算,换值, 编码等
位运算的基础知识:
- 操作数是32位整数
- 自动转化为整数
- 在二进制下进行运算
一.按位与&
判断奇偶数:
- 奇数: num & 1 == 1
- 偶数: num & 1 == 0
基本知识:
- 用法:
操作数1 & 操作数2 - 规则:有 0 则为 0,双 1 则为 1
- 原理:先将
操作数1和操作数2转为二进制数,按照第2步进行计算
二.按位或|
按位或|取整
- num | 0
eg: 5.23 | 0 => 5.23 | 0的结果是5
按位或|
- 自身|自身=自身,可以比较数值相等(仅限于整数)

三.按位非~
按位非远算符(~),反转操作数的位. 表象是对数字为负, 然后减去1(-x-1)
eg: ~9 = -9 -1 = -10
按位非~: 判断数组中是否包含某个元素
- 不存在, indexOf返回-1
- ~-1 = -(-1)-1=1-1=0
- ~arr.indexOf(val) => 数组中存在val这个值时~arr.indexOf(val) !==0; 数组中不存在这个元素时 ~arr.indexOf(val)===0;
- if(~arr.indexOf(val)) {} // 如果数组中存在val

按位非~取整
- ~~x
eg: ~~5.5677878 // 5

四.按位异或^
按位异或^ 归零律,恒等律,自反,集合律
- 归零律: a^a=0; 自己异或自己,位数上的值肯定相同
- 恒等律:a^0=a; 自己异或自己, 自己是啥结果是啥
- 自反: a^a^a=0^a = a; a三次^等于它自己
- 集合律: a^b^c == c^b^a, 与顺序无关
按位异或^ 值交换
- 变量值为数字,完成值的交换(不用增加临时变量)
示例:
let a = 10
let b = 20
a^=b //=> a = b^a => a^b
b^=a //=> b = a^b => (a^b) ^b => a ^ (b^b) => a ^ 0 => a => 结果是b=a
a^=b //=> a = b^a => b^b^b ^ (a^a) => b ^ 0 => b =>结果是: a = b
console.log('a:', a) // 20
console.log('b:', b) // 10
五.左移运算符:<<
<< 运算符执行左移位运算。
在移位运算过程中,符号位始终保持不变。
如果右侧空出位置,则自动填充为 0;
超出 32 位的值,则自动丢弃
console.log(5 << 2); // 20
基本知识:
- 用法:
操作数1 << 左移位数 - 规则:符号位不变,按位左移,右边补0
- 原理:先把
操作数1转换为二进制数
六.右移运算符:>>
>> 运算符执行有符号右移位运算。
与左移运算操作相反,它把 32 位数字中的所有有效位整体右移,再使用符号位的值填充空位。
移动过程中超出的值将被丢弃。
console.log(1000 >> 8); // 3
基本知识:
- 用法:
操作数1 >> 右移位数 - 规则:符号位不变,按位右移,左边补0
- 原理:先把
操作数1转换为二进制数
七.二进制和十进制互转方法:
因为计算机很多运算都直接或间接涉及二进制, 所以提一下相关知识:
7-1: 人工计算法则:
7-1-1: 二进制转十进制:
- 小数点: 从右到左用二进制的每个数乘以2的相应次方递增
- 小数点后: 从左到右用二进制的每个数乘以2的相应负次方递增
eg: 将1001.011转换为十进制?
整数部分(从右向左): 1*2^0 + 0*2^1+0*2^2+1*2^3=1+0+0+8=9
小数部分(从左到右): 0*2^-1+1*2^-2+1*2-3=0+1/4+1/8=0+0.25+0.125=0.375
注意: 这里的^不是位移符,是代表数字里的某某次方,比如2^3代表2的3次方
所以1001.011转换为十进制的数字是9.375
7-1-2: 十进制转换二进制:
- 整数: 除2取余,逆序排列
- 乘2取整,顺序排列
比如9.375
整数部分:
9 / 2 => 商4, 余1
4 / 2=> 商2, 余0
2 / 2=> 商1, 余0
1/2=> 商0, 余1

小数部分: 0.375
0.375 * 2 => 0.75 => Math.floor => 0(小于1, 所以继续)
0.75 * 2 => 1.5 => Math.floor => 1(但是余下0.5,继续)
0.5 * 2 => 1 => Math.floor => 1 (如果得到整数1, 没有小数部分就结束)

所以9.375转化为二进制数字是1001.011
7-2: JavaScript提供的二进制与十进制互转方法:
1. 二进制转十进制方法: parseInt
parseInt(string, radix)
eg: console.log(parseInt(1010,2)); // 10
如果是小数, 没有现成的方法, 需要代码:
// 小数部分 => 数字*(2的index次方)
function eachBinaryDigitPartToDecimal(binaryDigitPartArr) {return binaryDigitPartArr.map((currentValue, index) => {return Number(currentValue) * Math.pow(2, (-(index + 1)))})
}
// 如果该二进制只有整数部分则直接用 parseInt(string, radix) 处理
function eachBinaryIntPartToDecimal(binaryDigit) {return parseInt(binaryDigit, 2)
}/**
* 将二进制小数(包含整数部分和小数部分)转换为十进制数
* @param binaryDigit 二进制数(可能是整数,也可能是小数)
*/
function floatToDecimal(binaryDigit) {// 如果该二进制只有整数部分则直接用 parseInt(string, radix) 处理if (Number.isInteger(binaryDigit)) {return eachBinaryIntPartToDecimal(binaryDigit)} else {// 将整数和小数部分的数字分开组成一个数组, 第一个元素是整数部分的数字, 第二个元素是小数部分的数字const binaryDigitNumArr = binaryDigit.toString().split(".")// 将二进制整数转换为十进制数const binaryIntParStr = binaryDigitNumArr[0]const decimalIntPartNum = eachBinaryIntPartToDecimal(binaryIntParStr)// 将二进制小数部分转换为十进制数const binaryDigitPartArr = binaryDigitNumArr[1].split("") // 将数字split成小数部分的每个数字作为元素的一元数组const eachDecimalFloatPartNum = eachBinaryDigitPartToDecimal(binaryDigitPartArr) // 数组的数字变成item * 2^(-index)const deciamlFloatPartNum = eachDecimalFloatPartNum.reduce((val, currentVal) => val + currentVal) // 数组元素相加return decimalIntPartNum + deciamlFloatPartNum}
}2. 十进制转二进制: 字符串.toString(2)
同理: 十进制转16进制是: 字符串.toString(16)
eg:
const number = 10
console.log(number.toString(2)); // 1010

运用场景:
rgb和16进制颜色相互转换:
function colorRGBToHex(rgb) {// split的参数可以是正则const rgbArr= rgb.split(/[^\d]+/)// ['', '数字1', '数字2', '数字3', '']const color = rgbArr[1] << 16 | rgbArr[2] << 8 | rgbArr[3];return `#${color.toString(16)}`
}
console.log(colorRGBToHex('rgb(204, 0, 255)'))// 16进制转rgb格式
function colorHexToRGB(hex) {// 转为6位的16进制, 0x??????let newHex = hex.replace('#', '0x'),r = newHex >> 16,g = newHex >> 8 & 0xff,b = newHex & 0xffreturn `rgb(${r},${g},${b})`
}
console.log(colorHexToRGB('#CC00FF'))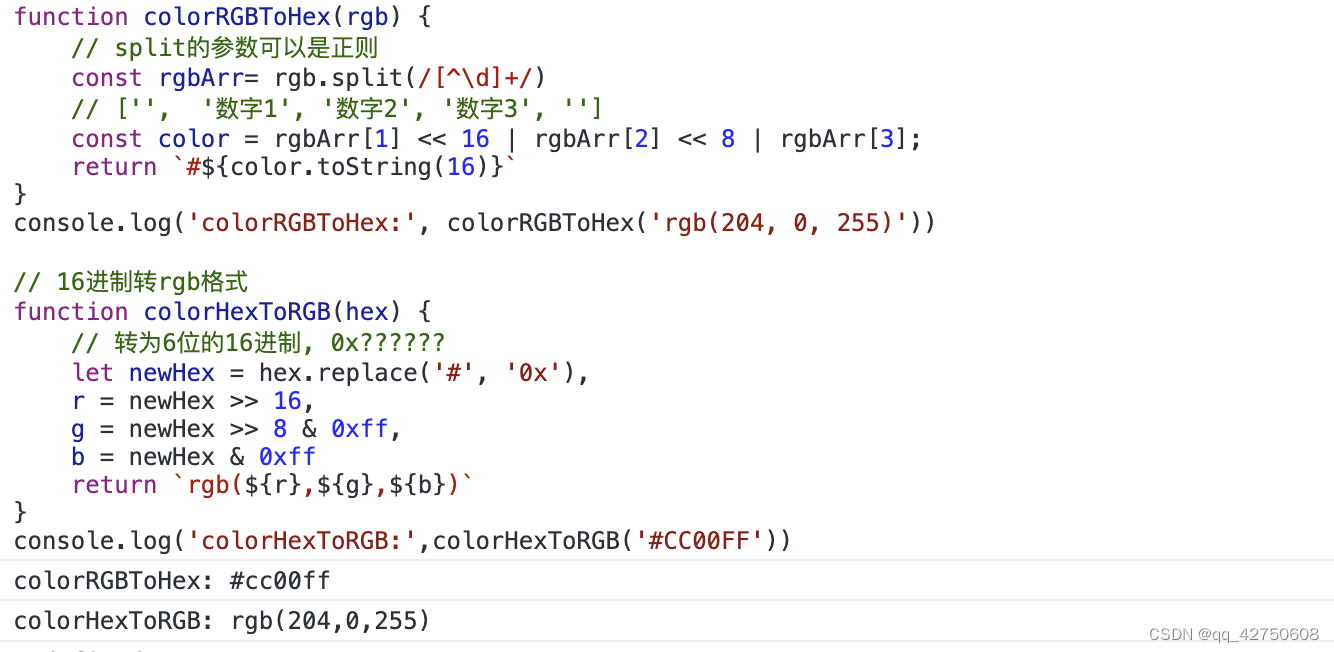
相关文章:

JavaScript位运算的妙用
位运算的妙用: 奇偶数, 色值换算,换值, 编码等 位运算的基础知识: 操作数是32位整数自动转化为整数在二进制下进行运算 一.按位与& 判断奇偶数: 奇数: num & 1 1偶数: num & 1 0 基本知识: 用法:操作数1 & 操作数2规则:有 0 则为…...
This dependency was not found: vxe-table/lib/vxe-table in ./src/main.js
描述 使用时 安装 npm install xe-utils vxe-table 引入 import Vue from vue import xe-utils import VXETable from vxe-table import vxe-table/lib/style.css vxe-table是一个基于 vue 的 PC 端表格组件, 支持增删改查、虚拟滚动、懒加载、快捷菜单、数据校验…...

网工内推 | H3C售前工程师,上市公司,13薪,有带薪年假、年终奖
01 长虹佳华 招聘岗位:高级售前工程师(H3C) 职责描述: 1. 负责公司签约代理的网络安全产品在区域的项目售前技术支持工作,包括项目售前交流、方案编写、招投标、产品测试等相关支持工作; 2. 与厂商产品部门…...
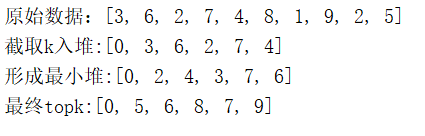
深入理解常见应用级算法思想
1 概论 1.1 概念 1.1.1 数据结构 1)概述 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。 2)划分 从关注的维度…...

Windows下使用pybind11教程(python调用C++代码)
1. 下载pybind11 gittub中下载,pybind下载后解压 2. C生成库文件 2.1.VS新建空白工程,工程名随意起 - 2.2更改目标文件名和配置类型 - 2.3更改目标文件拓展名 2.4添加include路径和库路径 包含目录中添加刚刚下载好的pybind的include路径以及pyhon的…...
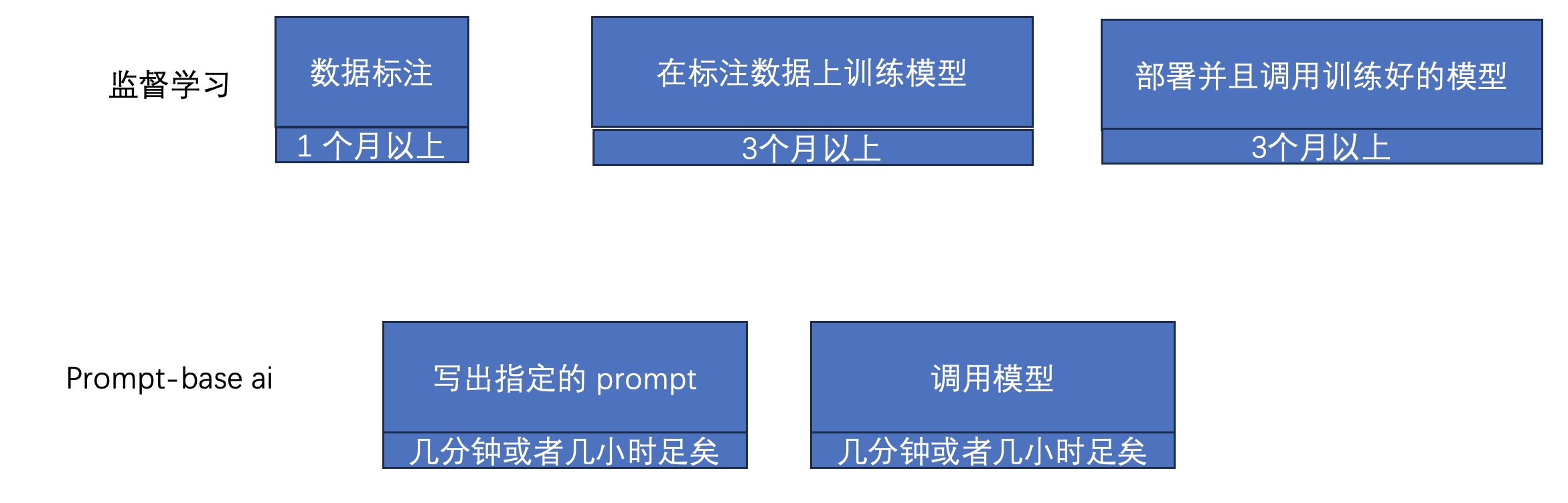
基于通用LLM的一次测试用例自动生成的实验
基于通用LLM的一次测试用例自动生成的实验 选择很多,最后选择了讯飞的星火做本次实验,原因还是因为讯飞的LLM的API是有免费额度的,案例代码相对比较成熟易学易用 1 LLM和基于LLM的应用 最近这段实际LLM已经变成了一个炙手可热的词汇,现在任何技术不了到LLM都感觉好像没有彻…...

【excel密码】为什么工作表不能移动、复制了?
为什么excel文件打开之后,工作表里是可以编辑的,但是想要移动工作表或者复制、重命名等操作,这是什么原因?其实这是因为设置了工作簿保护,设置了保护的工作簿无法对整张工作表进行操作。 想要取消这种保护,…...

软考高级之系统架构师之计算机基础
概述 今天是9月28日,距离软考高级只剩37天,加油! 概念 三种周期: Clock Cycle:时钟周期,CPU主频,又称为时钟频率,时钟周期是时钟频率的倒数Instruction Cycle:指令周…...

Mysql生产随笔
目录 1. Mysql批量Kill删除processlist 1.1查看进程、拼接、导出、执行 1.2常见错误解决方案 2.关于时区 3.内存占用优化 记录一下生产过程中的一些场景和命令使用方法,不定期进行更新 1. Mysql批量Kill删除processlist 1.1查看进程、拼接、导出、执行 sho…...

现代卷积网络实战系列2:PyTorch构建训练函数、LeNet网络
🌈🌈🌈现代卷积网络实战系列 总目录 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 1、MNIST数据集处理、加载、网络初始化、测试函数 2、训练函数、PyTorch构建LeNet网络 3、PyTorch从零构建AlexNet训练MNIST数据…...

leetCode 62.不同路径 动态规划 + 空间复杂度优化
62. 不同路径 - 力扣(LeetCode) 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” …...
在 .NET 8 Release Candidate 1 中推出 .NET MAUI:质量
作者:David Ortinau 排版:Alan Wang 今天,我们很高兴地宣布 .NET MAUI 在 .NET 8 Release Candidate 1 中已经可用,该版本带有适用于生产应用程序的正式许可证,因此您可以放心地将此版本用于生产环境。我们在 .NET 8 中…...

Spring 学习(八)事务管理
1. 事务 1.1 事务的 ACID 原则 数据库事务(transaction)是访问并可能操作各种数据项的一个数据库操作序列。事务必须满足 ACID 原则——即原子性(Atomicity)、一致性(Consistency)、隔离性(Iso…...
(A - E))
CodeTON Round 6 (Div 1 + Div 2, Rated, Prizes!)(A - E)
CodeTON Round 6 (Div. 1 Div. 2, Rated, Prizes!)(A - E) CodeTON Round 6 (Div. 1 Div. 2, Rated, Prizes!) A. MEXanized Array(分类讨论) 可以发现当 n < k 或者 k > x 1 的时候无法构成 , 其余的时候贪心的用 x 最大化贡献即…...
——Spring三级缓存的作用分别是什么?)
Spring 源码分析(五)——Spring三级缓存的作用分别是什么?
Spring 的三级缓存是经典面试题,也会看到一些文章讲三级缓存与循环依赖之的关系。那么,三级缓存分别存储的什么呢?他们的作用又分别是什么? 一、一、二级缓存 一级缓存是一个名为 singletonObjects 的 ConcurrentHashMap&#x…...

Django基于类视图实现增删改查
第一步:导入View from django.views import View 第二步:新建这个基类 class CLS_executer(View):db DB_executerdef get(self, request):executer_list list(self.db.objects.all().values())return HttpResponse(json.dumps(executer_list), conte…...
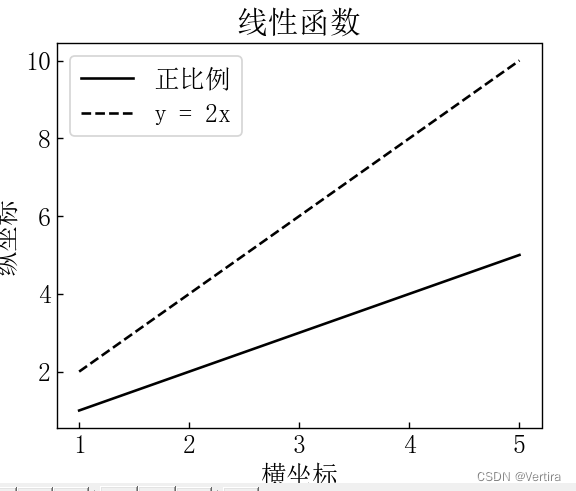
matplotlib绘图实现中文宋体的两种方法(亲测)
方法一:这种方法我没有测试。 第一步 找宋体字体 (win11系统) 2.matplotlib字体目录,如果不知道的话,可以通过以下代码查询: matplotlib.matplotlib_fname() 如果你是Anaconda3 安装的matplotlib&#x…...

非常有用的JavaScript高阶面试技巧!
🍀一、闭包 闭包是指函数中定义的函数,它可以访问外部函数的变量。闭包可以用来创建私有变量和方法,从而保护代码不受外界干扰。 // 例1 function outerFunction() {const privateVariable "私有变量";function innerFunction()…...
windows 安装Linux子系统 Ubuntu 并配置python3
环境说明: Windows 11 Ubuntu 20.04.6 安装步骤以及问题: 1、开启Windows Subsystem for Linux dism.exe /online /enable-feature /featurename:Microsoft-Windows-Subsystem-Linux /all /norestart 2、开启虚拟机特性 dism.exe /online /enabl…...
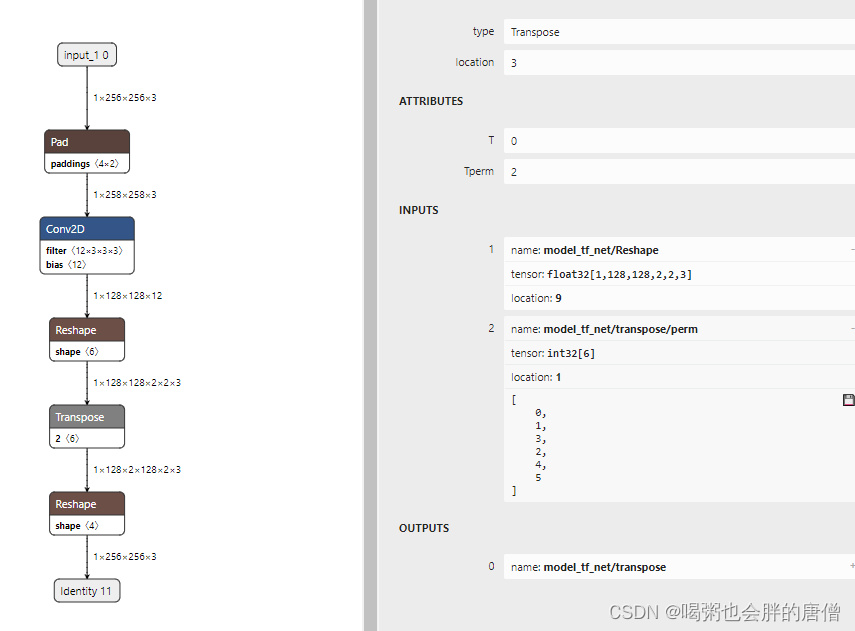
pytorch的pixel_shuffle转tflite文件
torch.pixel_shuffle()是pytorch里面上采样比较常用的方法,但是和tensoflow的depth_to_space不是完全一样的,虽然看起来功能很像,但是细微是有差异的 def tf_pixelshuffle(input, upscale_factor):temp []depth upscale_factor *upscale_f…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

