CodeTON Round 6 (Div 1 + Div 2, Rated, Prizes!)(A - E)
CodeTON Round 6 (Div. 1 + Div. 2, Rated, Prizes!)(A - E)
CodeTON Round 6 (Div. 1 + Div. 2, Rated, Prizes!)
A. MEXanized Array(分类讨论)
可以发现当 n < k 或者 k > x + 1 的时候无法构成 , 其余的时候贪心的用 x 最大化贡献即可 , 注意特判 k == x 的情况。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int t , n , k , x; signed main(){IOScin >> t;while(t --) {cin >> n >> k >> x;if(n < k || k > x + 1) {cout << "-1\n";} else {int res = 0;int now = k - 1;res += (now + 1) * now / 2;if(k == x) res += (x - 1) * (n - k);else res += x * (n - k);cout << res << "\n";}}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
B. Friendly Arrays(位运算)
观察或运算发现 , 只有当前位为 1 的时候或运算才能对结果产生影响 , 且是把所有数当前位全部变成 1 , 不妨对 n 的奇偶进行讨论 ,模拟完可以发现这样的一个性质 , 当 n 为奇数的时候操作异或和会变大 , 偶数的时候操作异或和会变小 , 所以最大最小值一定是全操作和全不操作的 , 计算即可。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int n , m , t;
int a[N] , b[N];signed main(){IOScin >> t;while(t --) {cin >> n >> m;int mx = 0 , mn = 0 , k = 0;for(int i = 1 ; i <= n ; i ++) cin >> a[i];for(int i = 1 ; i <= m ; i ++) cin >> b[i] , k |= b[i];for(int i = 1 ; i <= n ; i ++) {mn ^= (a[i] | k);mx ^= a[i];}if(mn > mx) swap(mn , mx);cout << mn << " " << mx << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
C. Colorful Table(思维 ,排序)
不难发现对于每个数来说 , 我们要找大于等于本身的最靠左的位置和最靠右的位置 , 考虑按照值的大小升序排序 , 这样问题就转化成找排序后每个值右边序号的最大值和最小值 , 逆序扫一遍 , 边扫便维护即可。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int t , n , k , ans[N];
struct node {int x , id;
}a[N];signed main(){IOScin >> t;while(t --) {cin >> n >> k;for(int i = 1 ; i <= n ; i ++) {cin >> a[i].x ;a[i].id = i;}sort(a + 1 , a + 1 + n ,[&](node a, node b){return a.x < b.x;});int mx = -9e18 , mn = 9e18;for(int i = n ; i >= 1 ; i --){int now = a[i].x;int id = a[i].id;mx = max(mx , id);mn = min(mn , id);ans[now] = (mx - mn + 1) * 2;}for(int i = 1 ; i <= k ; i ++) {cout << ans[i] << " ";ans[i] = 0;}cout << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
D. Prefix Purchase(贪心)
首先不难想到,贪心的取次数最多且最靠右的位置 , 但这样显然不是最优的 , 因为有
3 4 5
11
这种情况 , 我们可以通过替换的方式更充分的利用余数 ,转化一下不难发现如何利用余数的问题和开始要求的问题是一样的(选 4 还是选 5去替换 3 就相当于 k = 2 时 , 选 1 还是 选 2 能让字典序变大) , 不断贪心的选把余数用完即可.
例如 :
3 4 5
11
第一次贪心之后会变成
0 1 2
2
第二次贪心之后会变成
0 0 1
0
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int t , n , k;
int a[N] , pre[N] , b[N];signed main(){IOScin >> t;while(t --) {cin >> n;pre[0] = 0;for(int i = 1 ; i <= n ; i ++) cin >> a[i] , pre[i] = 0;cin >> k;int id = 0;while(k && id != -1) {int maxx = 0 , id1 = -1;for(int i = n ; i >= id + 1 ; i --) {if((k / a[i]) > maxx) {maxx = k / a[i];id1 = i;} }k -= maxx * a[id1];for(int i = n ; i >= id1 + 1 ; i --) {a[i] -= a[id1];}pre[id] += maxx;pre[id1] -= maxx;id = id1;}int sum = 0;for(int i = 1 ; i <= n ; i ++) {sum += pre[i - 1];cout << sum << " ";}cout << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
E. Another MEX Problem(dp)
先考虑 O(n^3) 的解决方法
d p [ i ] [ j ] 表示前 i 个数是否能表示出 j dp[i][j] 表示前 i 个数是否能表示出 j dp[i][j]表示前i个数是否能表示出j
考虑转移
若当前位不选进区间 dp[i][j] = dp[i - 1][j];
若当前位选进区间 , 枚举以当前位为右边界的区间 , 进行转移
dp[i][j] |= dp[l - 1][j ^ mex[l][i]]
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 5e3 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int t , n ;signed main(){IOScin >> t;while(t --) {cin >> n; vector<int>a(n + 1);for(int i = 1 ; i <= n ; i ++) {cin >> a[i];}vector<vector<int>>mex(n + 1 , vector<int>(n + 1));vector<vector<bool>>dp(n + 1 , vector<bool>(1 << 13));for(int i = 1 ; i <= n ; i ++) {int now = 0;vector<bool>vis(n + 1);for(int j = i ; j <= n ; j ++) {vis[a[j]] = 1;while(vis[now]) now += 1;mex[i][j] = now; }}dp[0][0] = 1;for(int i = 1 ; i <= n ; i ++) {//从上一位自然转移dp[i] = dp[i - 1]; for(int l = 1 ; l <= i ; l ++) {for(int k = 0 ; k < (1 << 13) ; k ++) {if(dp[l - 1][k]) dp[i][k ^ mex[l][i]] = 1;}}}int res = 0;for(int i = 0 ; i < (1 << 13) ; i ++) {if(dp[n][i]) res = max(res , i);}cout << res << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
考虑优化:
1:首先对于相同的右边界 , 我们枚举左边界的时候从大到小 , 由于我们是先从大的范围开始枚举 , 所以每个 mex 只更新一次即可。
2.其次对于相同的左边界 , 每个 mex 更新一次即可 。
显然能凑出来的mex的数量级是O(n)的 , 更新次数也是O(n)的
总复杂度
O ( n 2 ) O(n^2) O(n2)
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 5e3 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int t , n ;signed main(){IOScin >> t;while(t --) {cin >> n;vector<int>a(n + 1);for(int i = 1 ; i <= n ; i ++) {cin >> a[i];}vector<vector<int>>mex(n + 1 , vector<int>(n + 1));vector<vector<bool>>dp(n + 1 , vector<bool>(1 << 13));for(int i = 1 ; i <= n ; i ++) {int now = 0;vector<bool>vis(n + 1);for(int j = i ; j <= n ; j ++) {vis[a[j]] = 1;while(vis[now]) now += 1;mex[i][j] = now; }}dp[0][0] = 1;vector<vector<bool>>visl(n + 1 , vector<bool>(1 << 13));vector<vector<bool>>visr(n + 1 , vector<bool>(1 << 13));for(int i = 1 ; i <= n ; i ++) {//从上一位自然转移dp[i] = dp[i - 1];for(int l = i ; l >= 1 ; l --) {if(visr[i][mex[l][i]]) continue;if(visl[l][mex[l][i]]) continue;visl[l][mex[l][i]] = 1;visr[i][mex[l][i]] = 1;for(int k = 0 ; k < (1 << 13) ; k ++) {if(dp[l - 1][k]) dp[i][k ^ mex[l][i]] = 1;}}}int res = 0;for(int i = 0 ; i < (1 << 13) ; i ++) {if(dp[n][i]) res = max(res , i);}cout << res << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
(A - E))
CodeTON Round 6 (Div 1 + Div 2, Rated, Prizes!)(A - E)
CodeTON Round 6 (Div. 1 Div. 2, Rated, Prizes!)(A - E) CodeTON Round 6 (Div. 1 Div. 2, Rated, Prizes!) A. MEXanized Array(分类讨论) 可以发现当 n < k 或者 k > x 1 的时候无法构成 , 其余的时候贪心的用 x 最大化贡献即…...
——Spring三级缓存的作用分别是什么?)
Spring 源码分析(五)——Spring三级缓存的作用分别是什么?
Spring 的三级缓存是经典面试题,也会看到一些文章讲三级缓存与循环依赖之的关系。那么,三级缓存分别存储的什么呢?他们的作用又分别是什么? 一、一、二级缓存 一级缓存是一个名为 singletonObjects 的 ConcurrentHashMap&#x…...

Django基于类视图实现增删改查
第一步:导入View from django.views import View 第二步:新建这个基类 class CLS_executer(View):db DB_executerdef get(self, request):executer_list list(self.db.objects.all().values())return HttpResponse(json.dumps(executer_list), conte…...
matplotlib绘图实现中文宋体的两种方法(亲测)
方法一:这种方法我没有测试。 第一步 找宋体字体 (win11系统) 2.matplotlib字体目录,如果不知道的话,可以通过以下代码查询: matplotlib.matplotlib_fname() 如果你是Anaconda3 安装的matplotlib&#x…...

非常有用的JavaScript高阶面试技巧!
🍀一、闭包 闭包是指函数中定义的函数,它可以访问外部函数的变量。闭包可以用来创建私有变量和方法,从而保护代码不受外界干扰。 // 例1 function outerFunction() {const privateVariable "私有变量";function innerFunction()…...
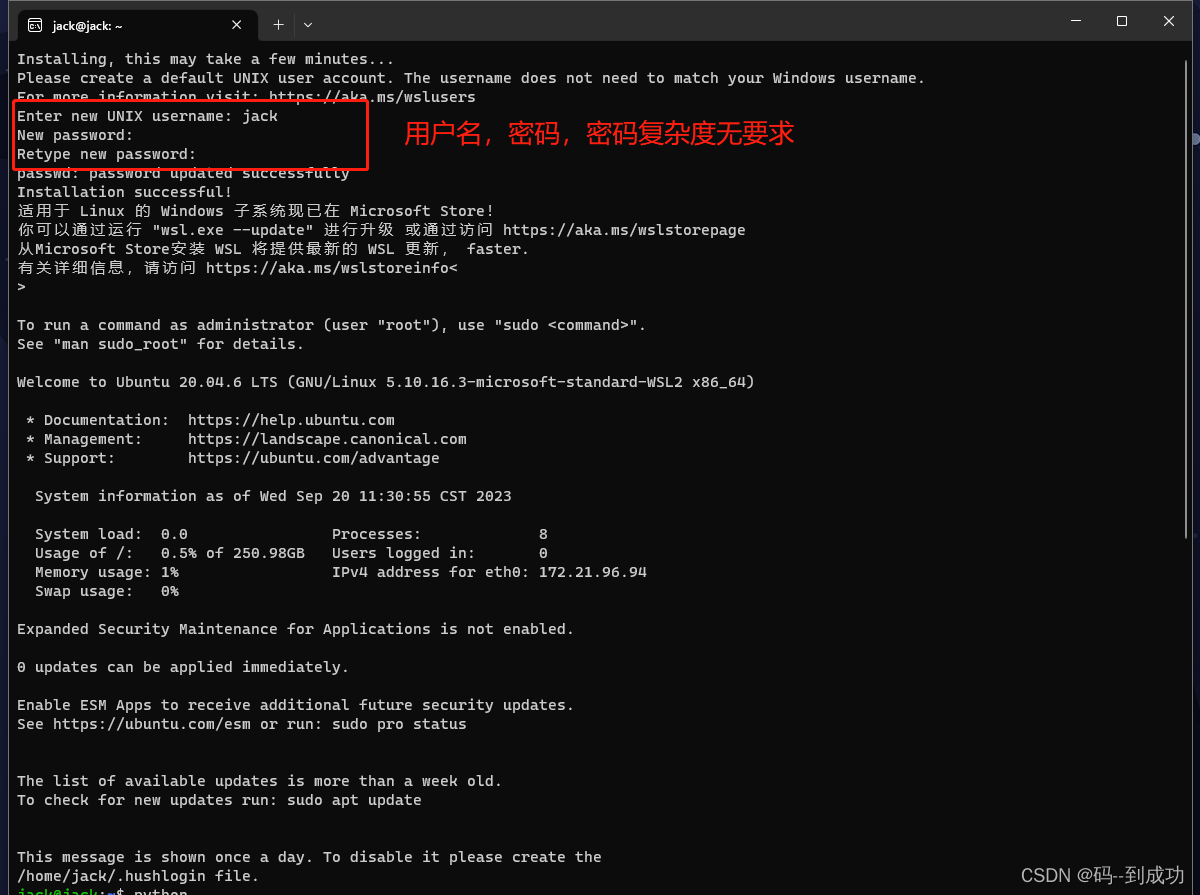
windows 安装Linux子系统 Ubuntu 并配置python3
环境说明: Windows 11 Ubuntu 20.04.6 安装步骤以及问题: 1、开启Windows Subsystem for Linux dism.exe /online /enable-feature /featurename:Microsoft-Windows-Subsystem-Linux /all /norestart 2、开启虚拟机特性 dism.exe /online /enabl…...
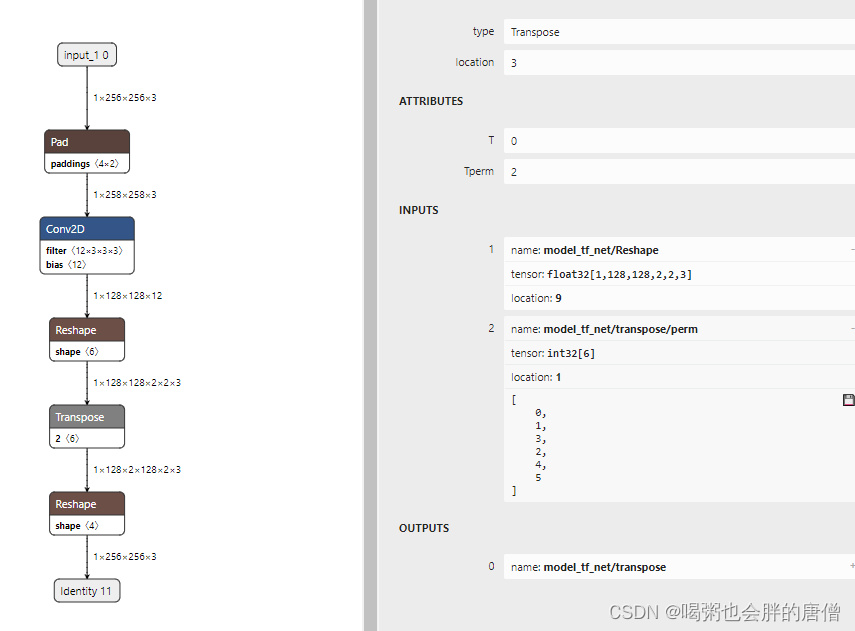
pytorch的pixel_shuffle转tflite文件
torch.pixel_shuffle()是pytorch里面上采样比较常用的方法,但是和tensoflow的depth_to_space不是完全一样的,虽然看起来功能很像,但是细微是有差异的 def tf_pixelshuffle(input, upscale_factor):temp []depth upscale_factor *upscale_f…...
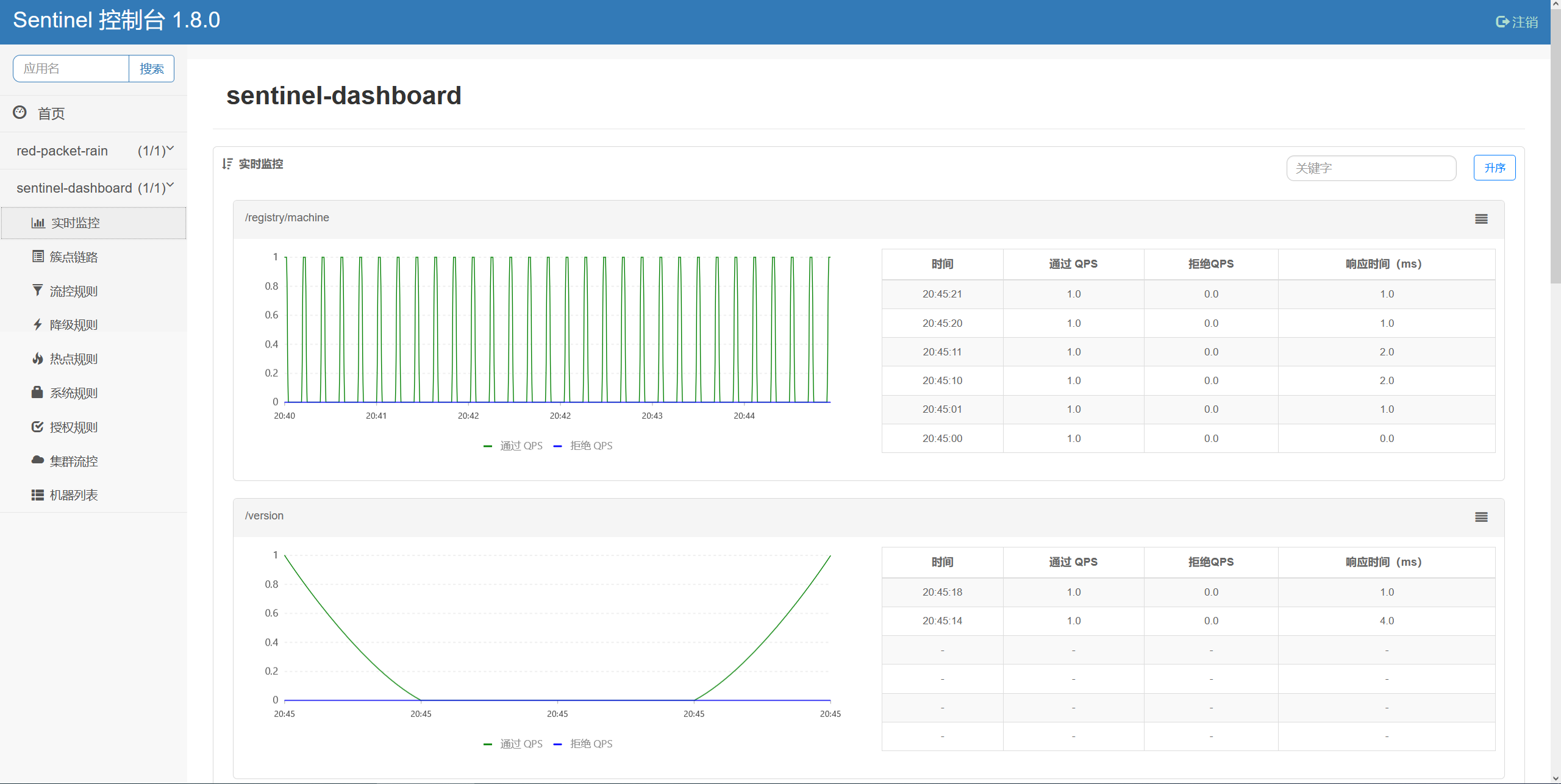
sentinel-dashboard-1.8.0.jar开机自启动脚本
启动阿里巴巴的流控组件控制面板需要运行一个jar包,通常需要运行如下命令: java -server -Xms4G -Xmx4G -Dserver.port8080 -Dcsp.sentinel.dashboard.server127.0.0.1:8080 -Dproject.namesentinel-dashboard -jar sentinel-dashboard-1.8.0.jar &…...

c++堆排序-建堆-插入-删除-排序
本文以大根堆为例,用数组实现,它的nums[0]是数组最大值。 时间复杂度分析: 建堆o(n) 插入删除o(logn) 堆排序O(nlogn) 首先上代码 #include<bits/stdc.h>using namespace std; void down(vector<int>&nums, int idx, i…...

使用代理后pip install 出现ssl错误
window直接设置代理 httphttp://127.0.0.1:7890;httpshttp://127.0.0.1...

护眼灯什么价位的好?最具性价比的护眼台灯推荐
到了晚上光线比较弱,这时候就需要开灯,要是孩子需要近距离看字学习等等,给孩子选择的灯具要特别的重视。护眼灯就是目前颇受学生家长青睐的灯具之一,越来越多的人会购买一个护眼灯给自己的孩子让孩子能够在灯光下学习的时候&#…...
vue event bus 事件总线
vue event bus 事件总线 创建 工程: H:\java_work\java_springboot\vue_study ctrl按住不放 右键 悬着 powershell H:\java_work\java_springboot\js_study\Vue2_3入门到实战-配套资料\01-随堂代码素材\day04\准备代码\08-事件总线-扩展 vue --version vue crea…...
深信服云桌面用户忘记密码后的处理
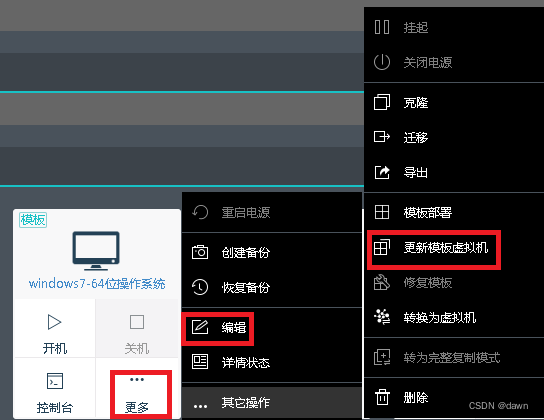
深信服云桌面用户忘记了密码,分两种情况,一个是忘记了登录深信服云桌面的密码,另外一个是忘记了进入操作系统的密码。 一、忘记了登录深信服云桌面的密码 登录虚拟桌面接入管理系统界面,在用户管理中选择用户后,点击后…...

Cocos Creator3.8 实战问题(一)cocos creator prefab 无法显示内容
问题描述: cocos creator prefab 无法显示内容, 或者只显示一部分内容。 creator编辑器中能看见: 预览时,看不见内容: **问题原因:** prefab node 所在的layer,默认是default。 解决方法&…...

朴素贝叶斯深度解码:从原理到深度学习应用
目录 一、简介贝叶斯定理的历史和重要性定义例子 朴素贝叶斯分类器的应用场景定义例子常见应用场景 二、贝叶斯定理基础条件概率定义例子 贝叶斯公式定义例子 三、朴素贝叶斯算法原理基本构成定义例子 分类过程定义例子 不同变体定义例子 四、朴素贝叶斯的种类高斯朴素贝叶斯&a…...

RUST 每日一省:闭包
Rust中的闭包是一种可以存入外层函数中变量或作为参数传递给其他函数的匿名函数。你可以在一个地方创建闭包,然后在不同的上下文环境中调用该闭包来完成运算。和一般的函数不同,闭包可以从定义它的作用域中捕获值。 语法 闭包由“||”和“{}”组合而成。…...

Ubuntu下文件的解压缩操作:常用zip和unzip
Ubuntu下文件的解\压缩 压缩一个文件夹为zip包,加参数-r: zip -r MyWeb.zip MyWeb需要排除目录里某个文件夹?例如我要去掉node_modules,以显著减小压缩包体积,此时该怎么做? zip -r MyWeb.zip ./MyWeb…...
Linux学习第22天:Linux中断驱动开发(一): 突如其来
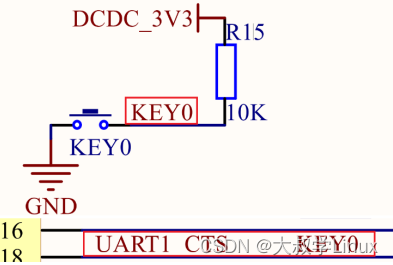
Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 中断作为驱动开发中很重要的一个概念,在实际的项目实践中经常用到。本节的主要内容包括中断简介、硬件原理分析、驱动程序开发及运行测试。其中驱动程…...
IDEA 2019 Springboot 3.1.3 运行异常
项目场景: 在IDEA 2019 中集成Springboot 3.1.3 框架,运行异常。 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSch…...
【JAVA】飞机大战
代码和图片放在这个地址了: https://gitee.com/r77683962/fighting/tree/master 最新的代码运行,可以有两架飞机,分别通过WASD(方向),F(发子弹);上下左右(控…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
