【学习笔记】LOJ #6240. 仙人掌
毒瘤题😅
简单版本 CF235D Graph Game
首先,考虑建立圆方树,然后对于一个点双(简单环)上的两个点,有两条路径可以到达
和简单版本类似,考虑容斥。即枚举点对 i , j i,j i,j之间 哪些路径是联通的 ,记固定下来的路径的并为 A A A,则 i , j i,j i,j之间通过 A A A联通的概率为 1 ∣ A ∣ \frac{1}{|A|} ∣A∣1。
然后就是神来之笔了:设 A A A中有 c n t cnt cnt个环,则容斥系数为 ( − 1 ) c n t (-1)^{cnt} (−1)cnt。证明:考虑 i , j i,j i,j之间实际有 k k k个环,则这个方案被计算了 ∑ x ≤ k 2 x ( k x ) ( − 1 ) k − x = ( 2 − 1 ) k = 1 \sum_{x\le k}2^x\binom{k}{x}(-1)^{k-x}=(2-1)^k=1 ∑x≤k2x(xk)(−1)k−x=(2−1)k=1次。
考虑在圆方树上 D P DP DP。因为点对之间的 L C A LCA LCA可能是方点或者圆点,因此不好统计。可以考虑直接枚举其中一个点,然后跑 D F S DFS DFS,复杂度 O ( n 3 ) O(n^3) O(n3)。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define fi first
#define se second
#define inf 0x3f3f3f3f
#define db double
using namespace std;
const int mod=998244353;
const int N=805;
int n,m,tot;
vector<int>G[N];
int dfn[N],low[N],ps[N][N],num;
ll res;
stack<int>s;
vector<int>G2[N];
void tarjan(int u){low[u]=dfn[u]=++num,s.push(u);for(auto v:G[u]){if(!dfn[v]){tarjan(v),low[u]=min(low[u],low[v]);if(low[v]>=dfn[u]){int tmp=0,d=0;tot++,G2[u].pb(tot),G2[tot].pb(u),ps[tot][u]=d++;do{tmp=s.top(),s.pop();G2[tot].pb(tmp),G2[tmp].pb(tot),ps[tot][tmp]=d++;}while(tmp!=v);}}else low[u]=min(low[u],dfn[v]);}
}
ll fpow(ll x,ll y=mod-2){ll z(1);for(;y;y>>=1){if(y&1)z=z*x%mod;x=x*x%mod;}return z;
}
ll f[N][N],fac[N],inv[N],invnum[N];
void init(int n){fac[0]=1;for(int i=1;i<=n;i++)fac[i]=fac[i-1]*i%mod;inv[n]=fpow(fac[n]);for(int i=n;i>=1;i--)inv[i-1]=inv[i]*i%mod;for(int i=1;i<=n;i++)invnum[i]=inv[i]*fac[i-1]%mod;
}
void add(ll &x,ll y){x=(x+y)%mod;
}
int sz[N];
void dfs(int u,int topf,int sz){for(int i=1;i<=sz;i++){if(f[u][i])add(res,invnum[i]*f[u][i]);}for(auto e:G2[u]){if(e==topf)continue;for(int i=0;i<G2[e].size();i++){if(i==ps[e][u])continue;int v=G2[e][i],l1=abs(ps[e][u]-ps[e][v])-1,l2=G2[e].size()-2-l1;for(int i=1;i<=sz;i++){add(f[v][i+l1+1],f[u][i]);add(f[v][i+l2+1],f[u][i]);add(f[v][i+l1+l2+1],-f[u][i]);}dfs(v,e,sz+l1+l2+1);}}
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m,init(n),tot=n;for(int i=1;i<=m;i++){int x,y;cin>>x>>y;G[x].pb(y),G[y].pb(x);}tarjan(1);for(int i=1;i<=n;i++){memset(f,0,sizeof f),f[i][1]=1,dfs(i,-1,1); }cout<<(res+mod)%mod;
}
相关文章:

【学习笔记】LOJ #6240. 仙人掌
毒瘤题😅 简单版本 CF235D Graph Game 首先,考虑建立圆方树,然后对于一个点双(简单环)上的两个点,有两条路径可以到达 和简单版本类似,考虑容斥。即枚举点对 i , j i,j i,j之间 哪些路径是联…...
)
java通过接口转发文件(上传下载)
java接口转发上传的文件 RequestMapping(value "/XXXX/fileUpload", method RequestMethod.POST) public String getFileUpload2(RequestParam("file") MultipartFile file, HttpServletRequest request) public static String hotMapPost3(String ur…...

Docker-部署docker-compose以及管理服务
部署docker-compose以及管理服务 文章目录 部署docker-compose以及管理服务[TOC] 前言一、docker-compose是什么?1、介绍2、 功能 二、安装docker-compose1.yum直接安装2.二进制安装3.pip安装 三、docker-compose部署服务1.编写docker-compose.yml文件 总结 前言 D…...

Android - Monkey 测试应用出现Crash报错IllegalStateException
问题描述 平时使用Lottie动画都是正常的,没出过这个crash问题,看下的报错信息,代码中文件夹也设置了,没看出来问题。 AndroidRuntime: java.lang.IllegalStateException: You must set an images folder before loading an imag…...
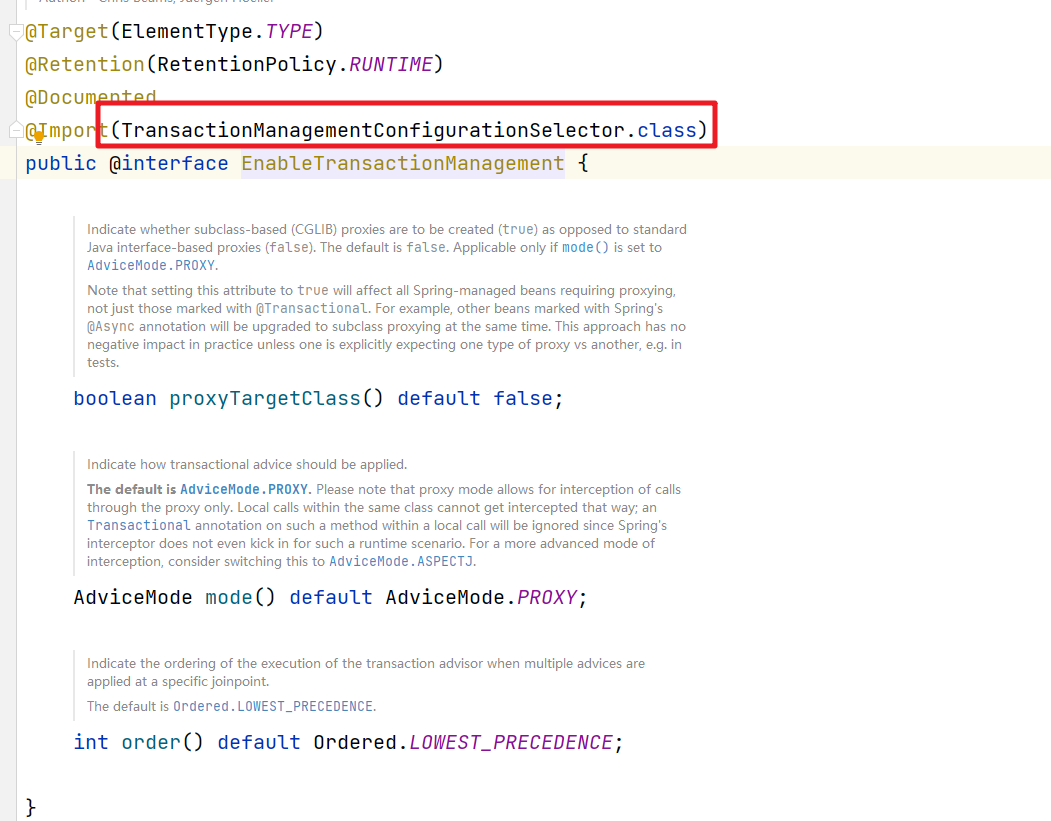
Spring源码分析 事务 实现原理
文章目录 什么是事务Spring事务管理Spring事务实现原理事务管理器事务定义事务的开启事务核心方法业务代码使用事务TransactionInterceptor 什么是事务 一般所指的事务是数据库事务,是指一批不可分割的数据库操作序列,也是数据库并发控制的基本单位。其…...
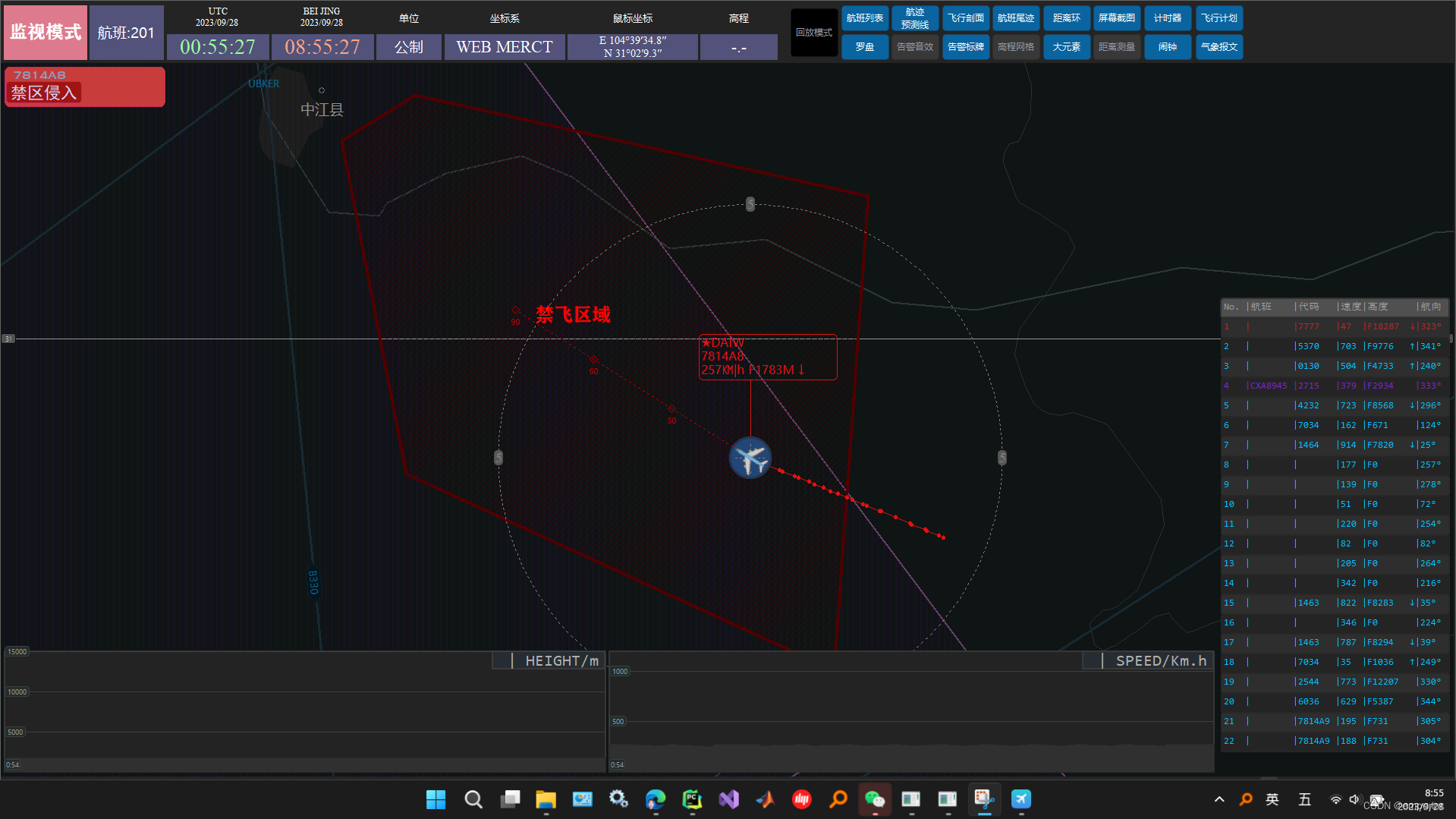
ADS-B及雷达显示终端8.3
新版本功能升级主要有如下: 1、地图更新 在上一版本8.2中使用的高程地图为由SRTM经过地形晕渲后,生成地形图片,然后对图片进行贴图,一一按规定位置、大小将地形图贴至底图上,而后在底图上进行二维矢量地图的绘制,包括…...
)
第二章:最新版零基础学习 PYTHON 教程(第二节 - Python 输入/输出–从 Python 控制台获取输入)
目录 Python 中的控制台是什么? 接受来自控制台的输入: 1. 将输入类型转换为整数:...
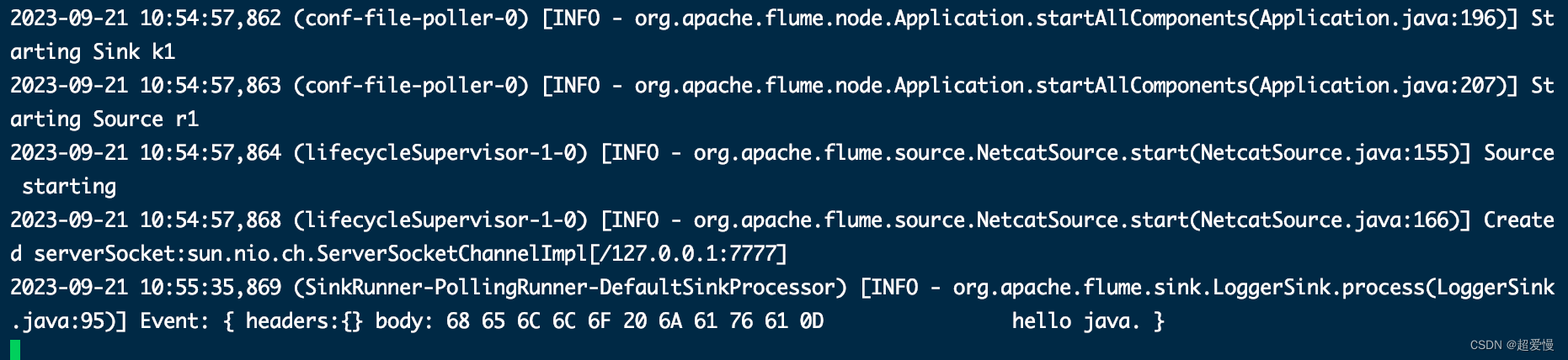
linux安装配置 flume
目录 一 解压安装包 二 配置部署 (1)修改配置 (2)下载工具 (3)创建配置文件 (4)启动监听测试 (5)flume监控文件 一 解压安装包 这里提供了网盘资源 链…...
)
SSM - Springboot - MyBatis-Plus 全栈体系(十五)
第三章 MyBatis 二、MyBatis 基本使用 4. CRUD 强化练习 4.1 准备数据库数据 首先,我们需要准备一张名为 user 的表。该表包含字段 id(主键)、username、password。创建SQL如下: CREATE TABLE user (id INT(11) NOT NULL AUT…...

win10默认浏览器改不了怎么办,解决方法详解
win10默认浏览器改不了怎么办,解决方法详解_蓝天网络 在使用Windows 10操作系统时,你可能会遇到无法更改默认浏览器的情况。这可能是因为其他程序或设置正在干扰更改。如果你也遇到了这个问题,不要担心,本文将为你提供详细的解决…...
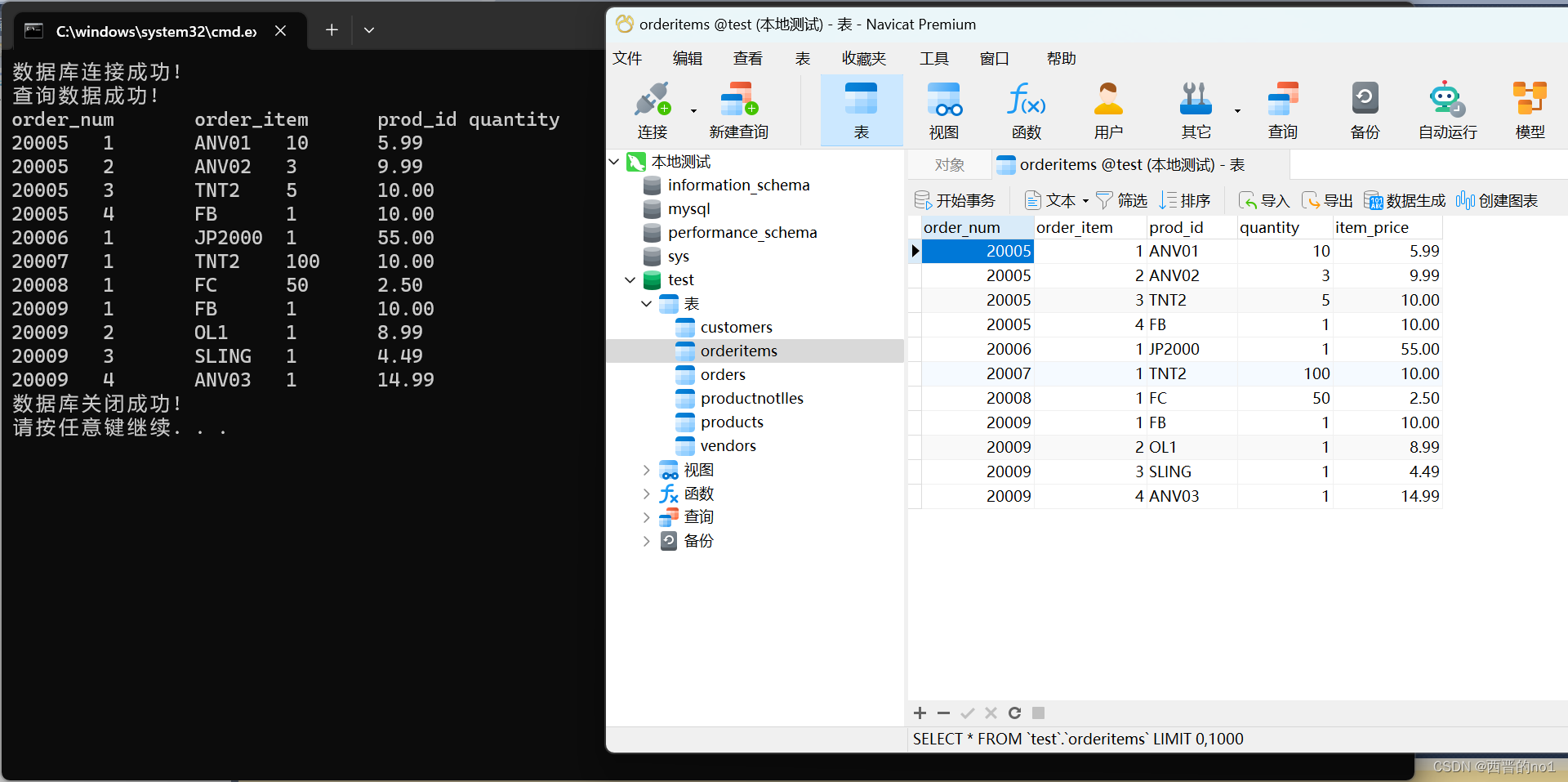
C语言连接MySQL并执行SQL语句(hello world)
1.新建一个控制台项目 参考【VS2022 和 VS2010 C语言控制台输出 Hello World】VS2022 和 VS2010 C语言控制台输出 Hello World_vs2022源文件在哪_西晋的no1的博客-CSDN博客 2.安装MySQL 参考【MySQL 8.0.34安装教程】MySQL 8.0.34安装教程_西晋的no1的博客-CSDN博客 3.复制MySQ…...
react实现动态递增展示数字特效
在可视化展示界面时有一种场景,就是页面在初始化的时候,有些数字展示想要从某个值开始动态递增到实际值,形成一种动画效果。例如: 写一个数字递增的组件,有两种方式:1.固定步长,代码如下&#x…...
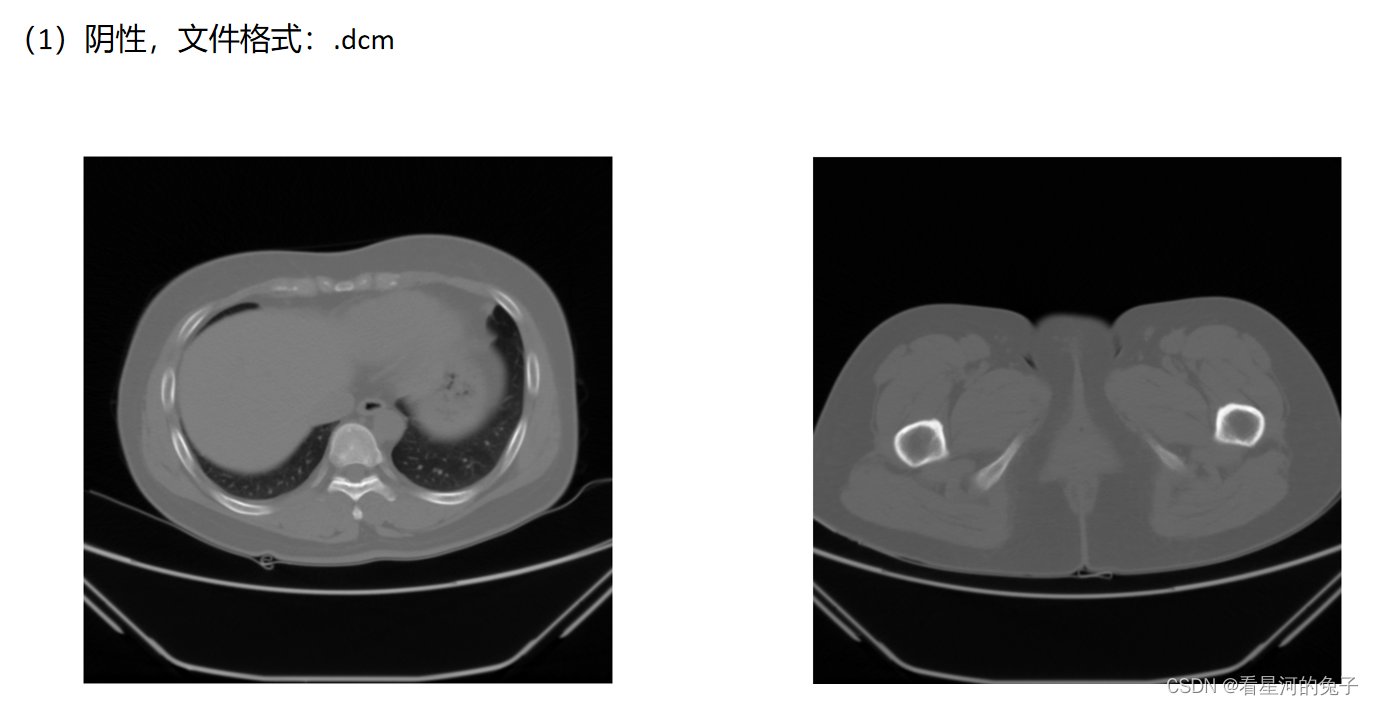
读取.nrrd和.dcm文件格式医学图片可视化与预处理
nrrd数据格式 MITK默认会将医学图像保存为格式为NRRD的图像,在这个数据格式中包含: 1、一个单个的数据头文件:为科学可视化和医学图像处理准确地表示N维度的栅格信息。 2、既能分开又能合并的图像文件。 nrrd_options输出 {u’dimension’:…...
VS CODE中的筛选器如何打开?
最近更新了vscode1.82版本,发现在git管理界面有一个“筛选器”功能,十分好用,后来关掉了,找了好久都没有找到办法打开这个筛选器功能,今天无意中不知道按到了哪个快捷键,打开了,就是下图这个&am…...

vue 多环境文件配置(开发,测试,生产)
1.经常我们在开发时候会有不同环境,要代理的路由等等都会出现不同 配置一下三个文件打包的时候,执行三个不同的指令就会打包不同的环境 npm run build:dev npm run build:test npm run build:prodpackage.json 中配置scripts 指令 以,env.development…...

在服务器上搭建pulseaudio的运行环境,指定其运行目录、状态目录和模块目录
如果想在搭建 PulseAudio 的服务器上指定其运行目录、状态目录和模块目录,可以通过修改 PulseAudio 的配置文件来实现。一般情况下所涉及的配置文件和相关选项如下所示: 1、配置文件路径:通常情况下,PulseAudio 的配置文件位于 /…...
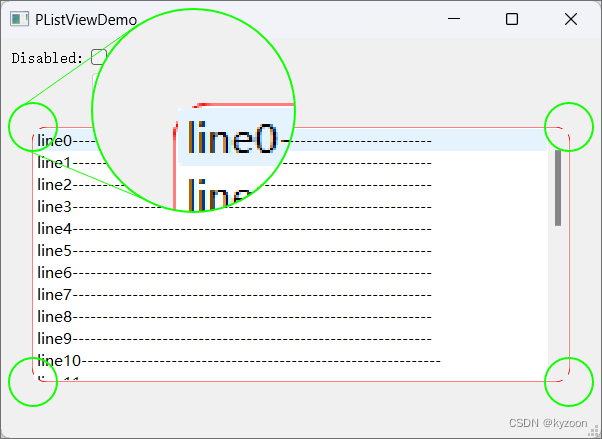
[Qt]QListView 重绘实例之一:背景重绘
0 环境 Windows 11Qt 5.15.2 MinGW x64 1 系列文章 简介:本系列文章,是以纯代码方式实现 Qt 控件的重构,尽量不使用 Qss 方式。 《[Qt]QListView 重绘实例之一:背景重绘》 《[Qt]QListView 重绘实例之二:列表项覆…...
国庆周《Linux学习第二课》
Linux开篇指南针环境安装(第一课)-CSDN博客 Linux详细的环境安装介绍在上面 第一 环境准备过程 安装过程...

6年前的麒麟980依旧可以再战
麒麟980,使用6年后的今天,我对它进行跑分测试。 在bench旗下的VRMark跑分中,麒麟980荣获5023分,同款跑分APP,要知道同一时期的高通骁龙855只有4937分, 打游戏,以和平精英为例,帧率3…...

JS计算任意多边形的面积
计算任意多边形的面积需要使用一些几何数学公式。具体的计算方法取决于多边形的形状和提供的顶点坐标。下面是一个通用的 JavaScript 函数,用于计算任意多边形的面积,假设你提供多边形的顶点坐标数组: function calculatePolygonArea(vertic…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...
