C++简单实现红黑树
目录
一、概念
二、红黑树的性质
三、红黑树的定义
四、红黑树的插入操作
情况一(叔叔节点存在且为红色)——变色+向上调整:
情况二(叔叔节点不存在或为黑色)——旋转+变色:
2.1叔叔节点不存在
2.2叔叔节点为黑色
插入的代码实现:
五、红黑树的验证
六、红黑树完整代码
一、概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或
Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路
径会比其他路径长出俩倍,因而是接近平衡的。
二、红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点必须是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

三、红黑树的定义
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode(const pair<K, V>& kv):_kv(kv),_right(nullptr),_left(nullptr),_parent(nullptr),_col(RED)//默认插入节点为红色,如果为黑色,就会对其他路径也造成影响{}pair<K, V> _kv;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _parent;Colour _col;
};C++STL中的set和map底层就是使用红黑树实现的,而map是存放键值对的,所以我们给红黑树的节点中的值存放一个键值对,以及左右孩子的指针和指向父节点的指针,还有一个存放颜色的标记。
四、红黑树的插入操作
红黑树的插入首先和普通二叉搜索树的插入操作一样,新建一个节点,左节点的值小于根,右节点的值大于根,找到位置进行插入。插入后应如果破坏了红黑树的性质,就需要进行调整。
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何
性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连
在一起的红色节点,此时需要对红黑树分情况来讨论:
我们给出一个约定:cur为当前节点,p为父亲节点,g为祖父节点,u为叔叔节点
情况一(叔叔节点存在且为红色)——变色+向上调整:
将p和u改成黑色,将g改为红色
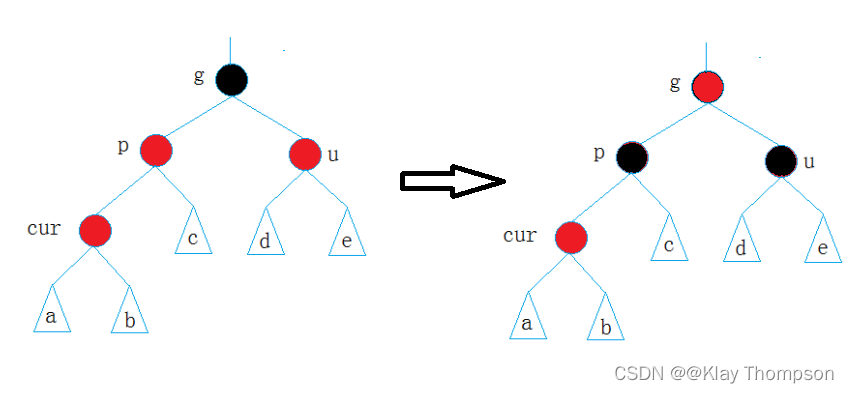
此时有三种情况:
1、g没有父亲节点,直接变成黑色就可以,插入结束;
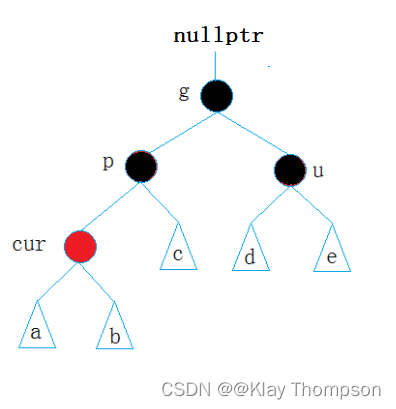
2、g有父亲节点,且父亲为黑色,插入结束;

3、g有父亲节点,且父亲为红色(违反了红色节点不能连续的性质),需要向上调整。
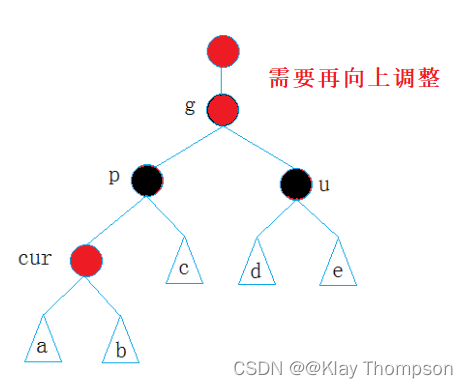
情况二(叔叔节点不存在或为黑色)——旋转+变色:
2.1叔叔节点不存在
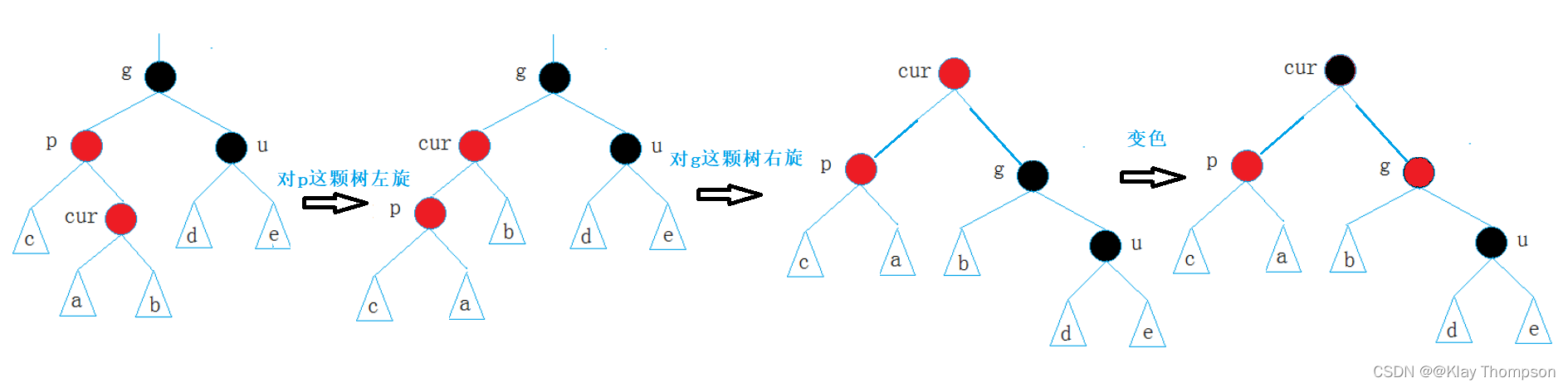
如果cur在parent的左边——右旋:
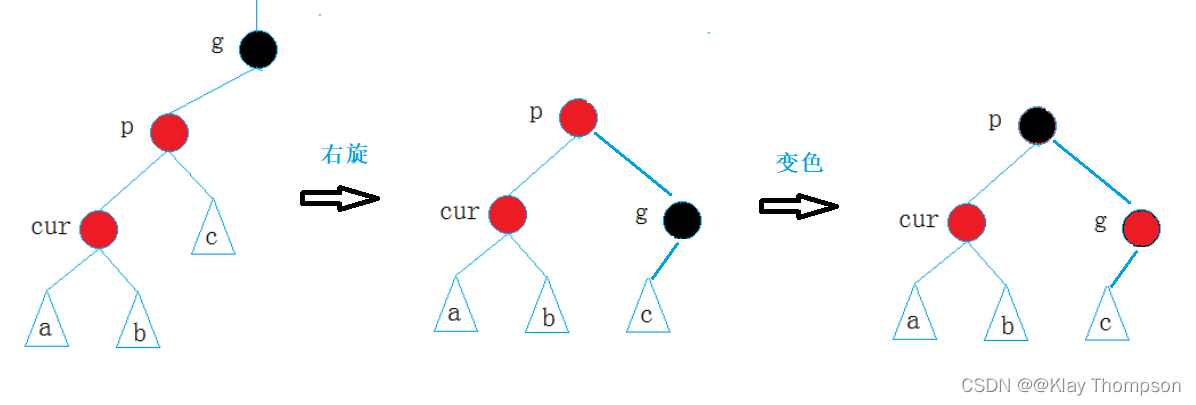
cur在parent的右边——先左旋再右旋:
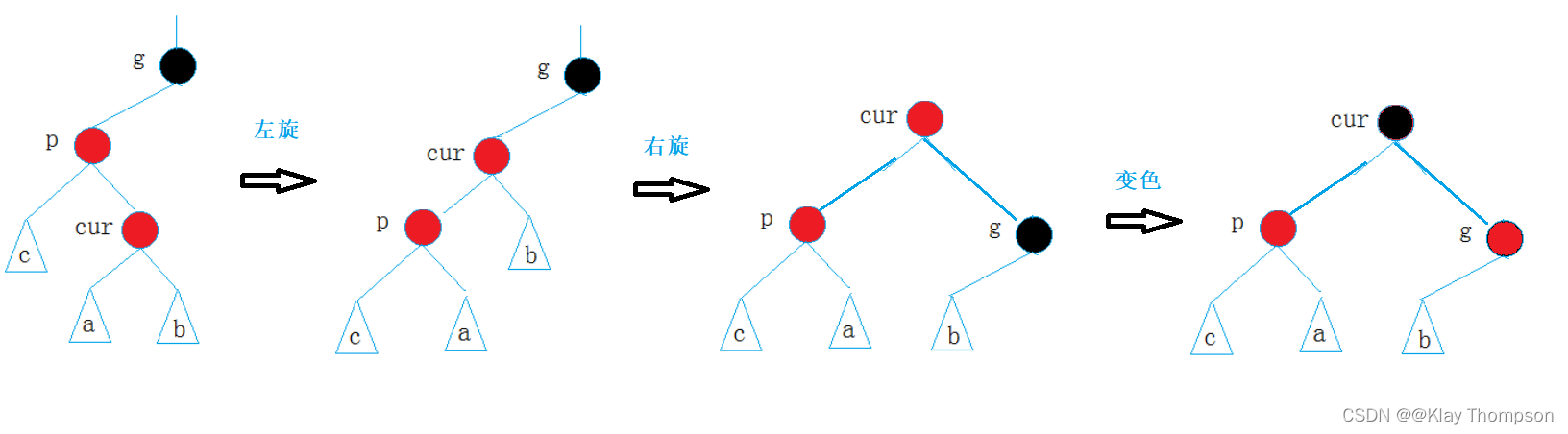
2.2叔叔节点为黑色
如果cur在parent的左边——右旋:

cur在parent的右边——先左旋再右旋:
以上插入操作是p在g节点左边的情况,p在g节点右边的情况与以上插入过程类似,仅仅是镜像翻转一下。

插入的代码实现:
左旋代码:
void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;cur->_left = parent;if (curleft)curleft->_parent = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){cur->_parent = nullptr;_root = cur;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}右旋代码:
void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;cur->_right = parent;if (curright)curright->_parent = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){cur->_parent = nullptr;_root = cur;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}插入代码:
bool insert(const pair<K, V>& kv){//如果root为空if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//插入Node* cur = _root;Node* parent = cur;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);//插入节点if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//插入完毕,开始调整颜色while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//叔叔在右if (grandfather->_left == parent){Node* uncle = grandfather->_right;//叔叔存在且为红色——变色if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//向上更新cur = grandfather;parent = cur->_parent;}//叔叔不存在或者为黑色——旋转+变色else{//右单旋即可if (parent->_left == cur){RotateR(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}//先左单旋,后右单旋else{RotateL(parent);RotateR(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}break;}}//叔叔在左else{Node* uncle = grandfather->_left;//uncle存在且为红色——变色if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//向上更新cur = grandfather;parent = cur->_parent;}//uncle不存在或为黑色——旋转+变色else{//左单旋即可if (parent->_right == cur){RotateL(grandfather);//变色grandfather->_col = RED;parent->_col = BLACK;}//先右单旋,再左单旋else{RotateR(parent);RotateL(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}五、红黑树的验证
bool isBalance(){return _isBalance(_root);}bool checkcolour(Node* root, int benckmark, int blackcount){if (root == nullptr){if (blackcount != benckmark)return false;return true;}if (root->_col == RED && root->_parent && root->_parent->_col == RED)return false;if (root->_col == BLACK)++benckmark;return checkcolour(root->_left, benckmark, blackcount)&& checkcolour(root->_right, benckmark, blackcount);}bool _isBalance(Node* root){if (root == nullptr)return true;if (root->_col != BLACK)return false;Node* cur = root;//求树中最左路径黑色节点的个数while (cur){if (cur->_col == BLACK)++blackcount;cur = cur->_left;}return checkcolour(_root, 0, blackcount);}六、红黑树完整代码
#pragma once#include <iostream>
#include <vector>
using namespace std;enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode(const pair<K, V>& kv):_kv(kv),_right(nullptr),_left(nullptr),_parent(nullptr),_col(RED)//默认插入节点为红色,如果为黑色,就会对其他路径也造成影响{}pair<K, V> _kv;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _parent;Colour _col;
};
/*
* 红黑树插入思路——关键在于uncle节点:
* 分为两大类:
* 一、如果uncle存在且为红色——仅仅变色即可
*
* g(黑) g(红)
* p(红) u(红) -------> p(黑) u(黑) ------->继续向上更新
* c(红) c(红)
*
*
* 二、如果uncle不存在或为黑色——旋转加变色
*
* 情况一: g(黑) p(红)
* p(红) NULL/黑 -------> c(红) g(黑)
* c(红)
*
* 仅仅右旋即可,g变成红色; p变成黑色; break;
*
* 情况二: g(黑) g(黑) c(红)
* p(红) NULL/黑 -------> 先左旋 c(红) -------> p(红) g(黑)
* c(红) p(红)
*
* c变成黑色,g变成红色,break;
*
* 情况三:情况一的对称图形
* 情况四:情况二的对称图形
*
*/
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:RBTree():_root(nullptr){}void InOrder(){cout << "InOrder: ";_InOrder(_root);cout << endl;}bool insert(const pair<K, V>& kv){//如果root为空if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//插入Node* cur = _root;Node* parent = cur;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);//插入节点if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//插入完毕,开始调整颜色while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//叔叔在右if (grandfather->_left == parent){Node* uncle = grandfather->_right;//叔叔存在且为红色——变色if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//向上更新cur = grandfather;parent = cur->_parent;}//叔叔不存在或者为黑色——旋转+变色else{//右单旋即可if (parent->_left == cur){RotateR(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}//先左单旋,后右单旋else{RotateL(parent);RotateR(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}break;}}//叔叔在左else{Node* uncle = grandfather->_left;//uncle存在且为红色——变色if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//向上更新cur = grandfather;parent = cur->_parent;}//uncle不存在或为黑色——旋转+变色else{//左单旋即可if (parent->_right == cur){RotateL(grandfather);//变色grandfather->_col = RED;parent->_col = BLACK;}//先右单旋,再左单旋else{RotateR(parent);RotateL(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}bool isBalance(){return _isBalance(_root);}private:bool checkcolour(Node* root, int benckmark, int blackcount){if (root == nullptr){if (blackcount != benckmark)return false;return true;}if (root->_col == RED && root->_parent && root->_parent->_col == RED)return false;if (root->_col == BLACK)++benckmark;return checkcolour(root->_left, benckmark, blackcount)&& checkcolour(root->_right, benckmark, blackcount);}bool _isBalance(Node* root){if (root == nullptr)return true;if (root->_col != BLACK)return false;Node* cur = root;while (cur){if (cur->_col == BLACK)++blackcount;cur = cur->_left;}return checkcolour(_root, 0, blackcount);}void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;cur->_left = parent;if (curleft)curleft->_parent = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){cur->_parent = nullptr;_root = cur;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;cur->_right = parent;if (curright)curright->_parent = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){cur->_parent = nullptr;_root = cur;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}
private:Node* _root;int blackcount = 0;
};测试:
运行结果:

之后更新红黑树的应用,用红黑树封装map和set。
相关文章:

C++简单实现红黑树
目录 一、概念 二、红黑树的性质 三、红黑树的定义 四、红黑树的插入操作 情况一(叔叔节点存在且为红色)——变色向上调整: 情况二(叔叔节点不存在或为黑色)——旋转变色: 2.1叔叔节点不存在 2.2叔叔…...
国庆加速度!新增功能点锁定功能,敏捷开发新增估算功能,助力项目快速突破!
大家好,CoCode开发云旗下Co-Project V3.6智能项目管理平台正式发布,平台新增功能点锁定功能、敏捷开发模式新增估算板块和两种估算方式。 功能点锁定功能进一步提高了项目估算的灵活性和准确性,有利于提高项目估算效率;而敏捷开发…...

uniapp 如何动态切换应用图标、名称
有时候我们需要实现类似百度网盘、淘宝APP这种可以动态切换 但是呢这种需求平常非常少见 很多人不知道如何操作 今天就教大家如何实现 这里我们需要用到一款插件Ba-ChangeIcon Ba-ChangeIcon 是一款uniapp动态切换应用图标、名称的插件。可实现过年、过节动态切换应用图标的效…...
CUDA学习笔记0929
一、GPU缓存和变量作用域 1. 缓存类型 (1)GPU缓存是非可编程存储区域 (2)GPU包含4类缓存: L1缓存,每个流处理器一个 L2缓存,全部流处理器共享一个 L1和L2都可用于存储本地和全局内存中的数…...

XML-Based Configuration Beans for Ioc Container
XML-Based Configuration XML-based configuration is the traditional way of configuring beans in Spring. <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"h…...

俞敏洪:董宇辉在北京有房子了!
据媒体报道,9月26日,俞敏洪在直播中透露,董宇辉已经在北京拥有了自己的房子,并且强调这是大家共同努力的结果。 这一消息引起了广泛关注和热议。在此之前,董宇辉曾在公开场合表示,俞敏洪老师为了给他凑钱买…...

蓝桥等考Python组别七级006
第一部分:选择题 1、Python L7 (15分) 下面for循环语句中,变量i的取值范围是( )。 for i in range(9): print(i) 1~90~91~80~8正确答案:D 2、Python L7 (15分) 下面哪一年是闰年?( &#...

港联证券:股市3000点什么意思?
近年来,股市风起云涌,上涨也好,下跌也罢,无一不让人心潮澎湃。但是,如果你听到股市3000点这个数字,你是否知道它意味着什么呢?接下来,我们将从商场体现、微观经济、投资者心态等方面…...
windows 下 vs code 格式化代码(clang-format)
vscode 的格式化代码能力来源于插件(有不止一种插件提供格式化功能),而非 vscode 本身 1、安装插件 2、windows 下载 LLVM-17.0.1-win64.exe (exe 结尾的安装包) Releases llvm/llvm-project GitHub 可以直接把这…...
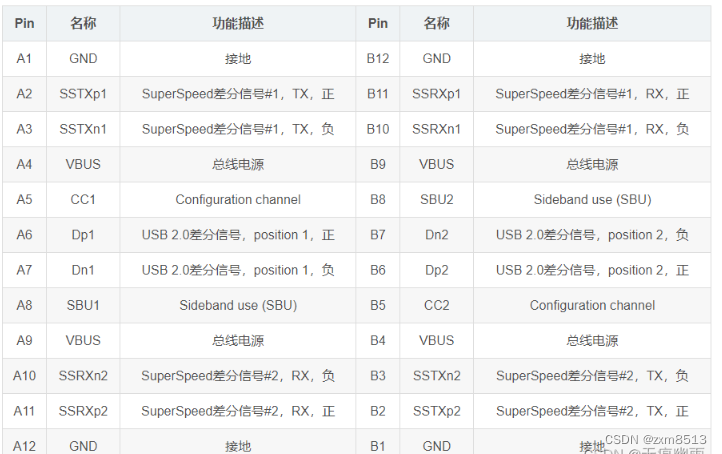
USB TypeC接口说明
USB TypeC 拥有诸多优点:双面可插不担心正反、可做USB/雷电高速传输载体,支持 PD快充、音频设备、HDMI传输、调试模式等诸多功能。 市面上的其他USB接口和充电接口在逐步被TypeC替代,可以预见的是,TypeC作为一种多兼容性接口,其未来会具有非常长的生命周期。 本文主要介…...

深眸科技入局AI视觉行业,以深度学习赋能视觉应用推进智造升级
随着科技的飞速发展,人工智能技术已经成为改变我们生活的重要力量,而深度学习作为人工智能的一个重要分支,近年来随着卷积神经网络的突破和推广,取得了显著进展,并呈现爆发式增长势头。 目前AI技术已经被迅速引入到机…...
基于微信小程序的校园失物招领系统设计与实现(源码+lw+部署文档+讲解等)
前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 👇🏻…...

蓝桥等考Python组别七级001
第一部分:选择题 1、Python L7 (15分) 下面for循环语句中,变量i的取值范围是( )。 for i in range(1, 10): print(i) 1~101~90~100~9正确答案:B 2、Python L7 (15分) 闰年是历法中的名词,包括普通闰年和世纪闰年两类:...
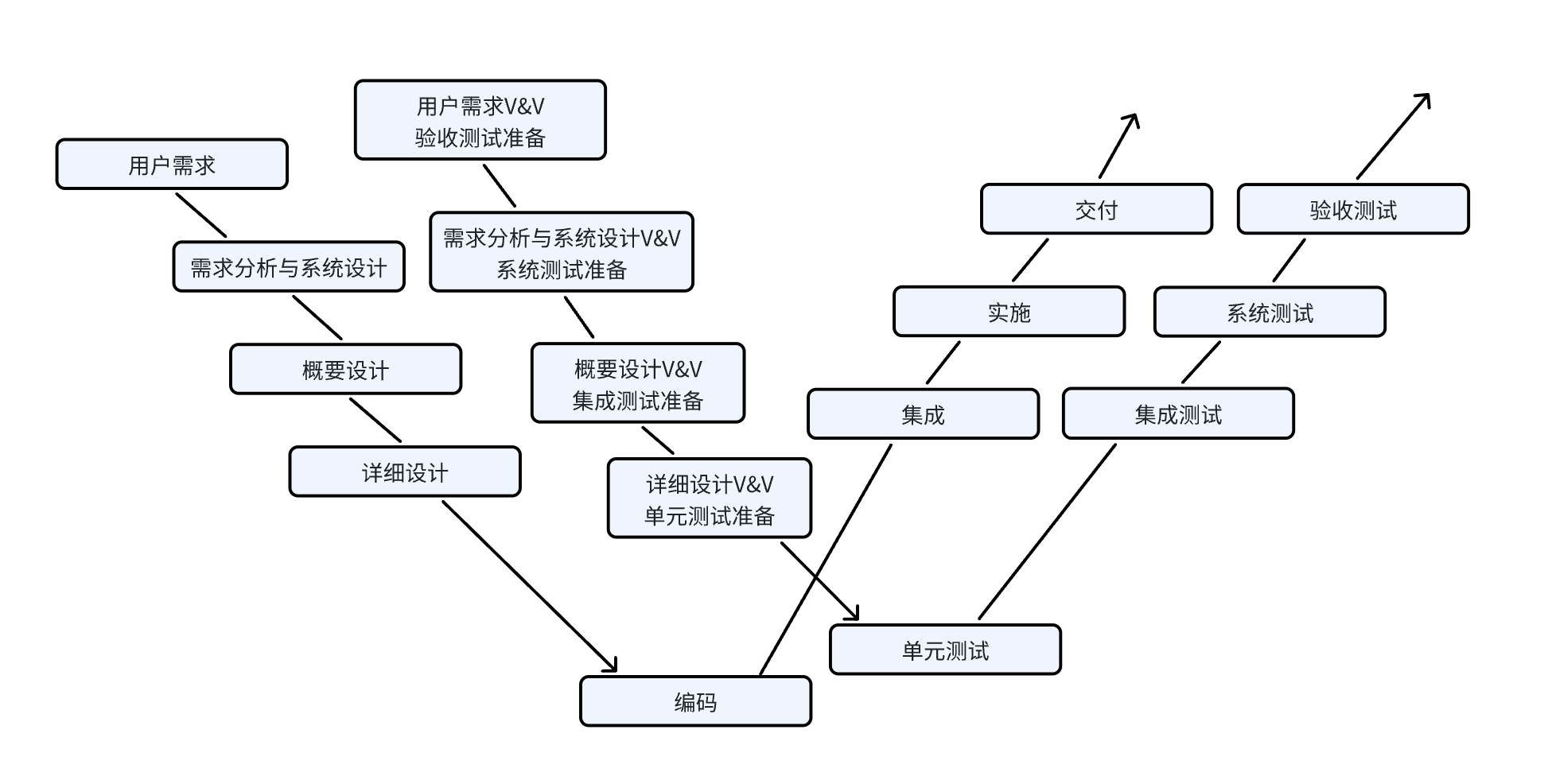
【软件测试】开发/测试模型
开发/测试模型 瀑布模型 设计:技术文档(设计那些接口,库表,mq,定时任务),UI视觉稿 特点:线性的结构。 优点:每个阶段做什么,产出什么非常清晰 缺点:测试人员介入太晚…...
用于时间触发的嵌入式软件的IDE
TTE Systems的RapidiTTy IDE为希望创建“时间触发”微控制器软件以提高整体系统可靠性的开发人员提供了一个独立的环境。RapidiTTy(下面的图1)旨在解决深度嵌入的应用,包括医疗,国防,汽车和工业部门以及白色和棕色商品…...
wordpress插件-免费的wordpress全套插件
在当今数字化时代,网站和博客已经成为信息传递、观点分享和商业交流的重要平台。在这个背景下,WordPress作为最受欢迎的内容管理系统之一,无疑扮演着至关重要的角色。然而,要保持一个成功的WordPress网站,不仅需要出色…...

第一百五十七回 SliverList组件
文章目录 概念介绍使用方法示例代码 我们在上一章回中介绍了沉浸式状态栏相关的内容,本章回中将介绍SliverList组件.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在这里介绍的SliverList组件是一种列表类组件,类似我们之前介绍过的L…...

数据结构与算法——17.二叉搜索树
这篇文章我们来看一下数据结构中的二叉搜索树。 目录 1.概述 2.二叉搜索树的实现 3.总结 1.概述 我们前面学到的数据结构,比如:动态数组、链表、队列、栈、堆,这些数据结构存储完数据后,我们要去查找某个数据,它的…...

rust所有权
一、堆和栈 栈和堆都是程序运行时使用的内存,但是它们的结构不同。 1.栈 栈,英文是stack。是内存的一段区域。 栈是后进先出形式的。就像薯片桶,先放进去的一片只能后拿出来。 栈上存储的数据大小必须是已知且固定的。也就是说如果一个变量…...
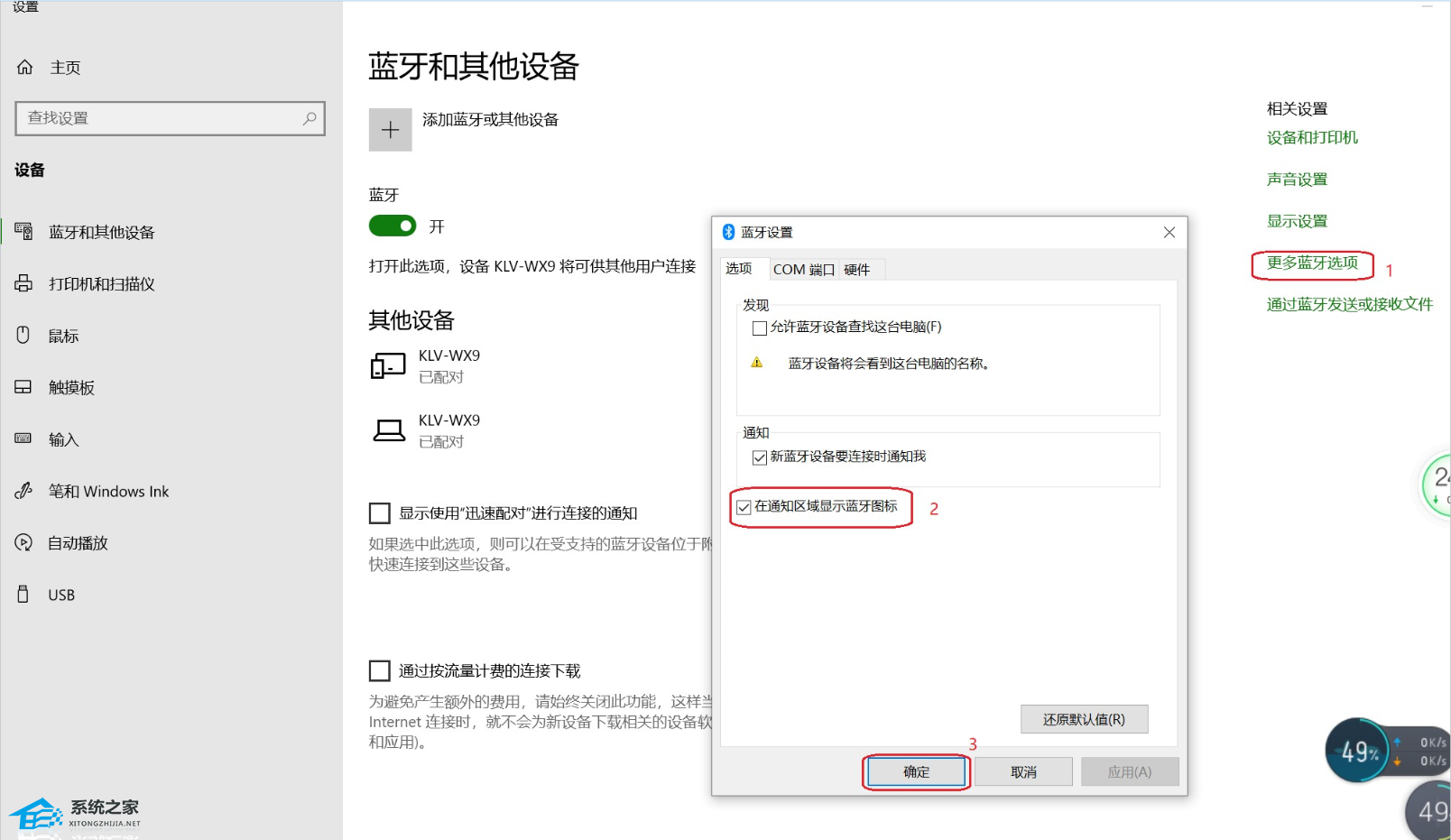
Win10电脑任务栏没有蓝牙图标的简单解决方法
Win10电脑任务栏没有蓝牙图标怎么办?在Win10电脑中,用户有时候会发现任务栏上没有蓝牙图标了,这样就无法通过蓝牙图标快速打开蓝牙服务了。下面小编给大家介绍最简单的解决方法,帮助大家找回任务栏上面的蓝牙图标吧。 问题原因 反…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
