数据结构与算法——17.二叉搜索树
这篇文章我们来看一下数据结构中的二叉搜索树。
目录
1.概述
2.二叉搜索树的实现
3.总结
1.概述
我们前面学到的数据结构,比如:动态数组、链表、队列、栈、堆,这些数据结构存储完数据后,我们要去查找某个数据,它的时间复杂度是O(n),因为这些数据结构的底层实现都是数组或者链表,都是线性的。我们前面有学过二分查找,它的最优时间复杂度为O(lngn)。下面,我们来学习另外一种便于查找的数据结构——二叉搜索树。
二叉搜索树:又被称为二叉查找树。其特点如下:
- 树节点上增加key属性,用来比较谁大谁小,key不可以重复
- 对于任意一个树节点,它的key比它的左子树的key都大,比它的右子树的key都小
下面看一张图:

二叉搜索树的理想查找时间复杂度为O(logn)
2.二叉搜索树的实现
下面来看一下二叉搜索树的实现:
二叉搜索树的根据key值找节点值,找最大,找最小,找前驱和后继都是比较简单的,思路都是很好理解的。
下面重点来讲一下删除的思路(删除的情况很多):
- 删除节点没有左孩子,将右孩子托孤给Parent
- 删除节点没有右孩子,将左孩于托孤给Parent
- 删除节点左右孩子都没有,已经被涵盖在情况1、情况2当中,把null 托孤给Parent
- 删除节点左右孩子都有,可以将它的后继节点(称为S)托孤给Parent,再称S的父亲为SP,又分两种情况:(1)SP就是被删除节点,此时D与S紧邻,只需将S托孤给Parent (2)SP不是被删除节点,此时D与S不相邻,此时需要将S的后代托孤给SP,再将S托孤给Parent
下面来看一下代码的具体实现(代码太长,就不截图展示了):
package Tree;import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;/**二叉搜索树*/
public class L2_BSTree1<T extends Comparable<T>> {/**节点类*/static class BSTNode<T>{T key;Object value;BSTNode left;BSTNode right;public BSTNode(T key) {this.key = key;}public BSTNode(T key, Object value) {this.key = key;this.value = value;}public BSTNode(T key, Object value, BSTNode left, BSTNode right) {this.key = key;this.value = value;this.left = left;this.right = right;}}BSTNode<T> root;//根节点/**根据key值得到节点的值*/public Object get(T key){BSTNode<T> node = root;while (node!=null){/*** 该值比传入参数大,返回1* 该值比传入参数小,返回-1* 该值等于传入参数,返回0* */int result = key.compareTo(node.key);if (result < 0){node = node.left;}else if (result > 0){node = node.right;}else {return node.value;}}return null;}public Object get1(T key){return doGet(root,key);}private Object doGet(BSTNode<T> node, T key){//递归的函数int result = key.compareTo(node.key);if (node == null){return null;}if (result < 0){return doGet(node.left,key);//向左找}else if (result > 0){return doGet(node.right,key);//向左找}else{return node.value;//返回当前的值}}/**得到最小key值所对应的值*/public Object min(){//非递归版return max(root);}public Object min(BSTNode node){//非递归版if (node == null){return null;}BSTNode pre = node;while (pre.left != null){pre = pre.left;}return pre.value;}public Object min1(){//递归版return doMin(root);}private Object doMin(BSTNode node){if (node == null){return null;}if (node.left == null){return node.value;}return doMin(node.left);}/**得到最大key值所对应的值*/public Object max(){//非递归版return max(root);}private Object max(BSTNode<T> node){if (node == null){return null;}BSTNode pre = node;while (pre.right != null){pre = pre.right;}return pre.value;}public Object max1(){//递归版return doMax(root);}private Object doMax(BSTNode node){if (node == null){return null;}if (node.right == null){return node.value;}return doMin(node.right);}/**存储key值和节点值*/public void put(T key,Object value){//1.如果key存在,更新操作//1.如果key不存在,新增操作BSTNode<T> node = root;BSTNode<T> parent = null;//记录key的前一个值while (node != null){parent = node;int result = key.compareTo(node.key);if (result < 0){node = node.left;}else if (result > 0){node = node.right;}else {//找到了node.value = value;return;}}//没找到,新增if (parent == null){root = new BSTNode<T>(key,value);}int result = key.compareTo(parent.key);if (result < 0){parent.left = new BSTNode<T>(key,value);}else if(result > 0){parent.right = new BSTNode<T>(key,value);}}/**找到某一个key的前驱值*/public Object predecessor(T key){BSTNode<T> p = root;BSTNode<T> ancestorFromLeft = null;while (p != null){int result = key.compareTo(p.key);if (result < 0){p = p.left;}else if (result > 0){ancestorFromLeft = p;p = p.right;}else {break;}}if (p == null){//没找到节点的情况return null;}if (p.left != null){//找到节点,有左子树return max(p.left);}return ancestorFromLeft != null ?ancestorFromLeft.value :null;}/**找到某一个key的后继值*/public Object successor(T key){BSTNode<T> p = root;BSTNode<T> ancestorFromRight = null;while (p != null){int result = key.compareTo(p.key);if (result < 0){ancestorFromRight = p;p = p.left;}else if (result > 0){p = p.right;}else {break;}}if (p == null){//没找到节点的情况return null;}if (p.right != null){//找到节点,有左子树return min(p.right);}return ancestorFromRight != null ?ancestorFromRight.value :null;}/**根据key值删除对应的节点*/public Object delete(T key){BSTNode<T> p = root;BSTNode<T> parent = null;while (p != null){int result = key.compareTo(p.key);if (result < 0){parent = p;//记录当前节点的父节点p = p.left;}else if (result > 0){parent = p;p = p.right;}else {break;}}if (p == null){return null;}//删除操作if (p.left == null ){//情况1shift(parent,p,p.right);} else if(p.right == null ){//情况2shift(parent,p,p.left);} else {//情况4BSTNode<T> s = p.right;BSTNode<T> sParent = p;//后继结点的父亲while (s.left != null){sParent = s;s = s.left;}if (sParent != p){//不相邻shift(sParent,s,s.right);s.right = p.right;}shift(parent ,p,s);s.left = p.left;}return p.value;}/*** 托孤方法* parent:被删除节点的父亲* deleted:被删除节点* child:被上去的结点* */private void shift(BSTNode<T> parent,BSTNode<T> deleted,BSTNode<T> child){if (parent == null){root = child;} else if (deleted == parent.left){parent.left = child;}else {parent.right = child;}}public Object delete1(T key){ArrayList<Object> Aresult = new ArrayList<>();//保存被删除节点的值root = doDelete(root,key,Aresult);return Aresult.isEmpty()? null:Aresult.get(0);}private BSTNode<T> doDelete(BSTNode<T> node,T key,ArrayList<Object> Aresult){//node:递归删除的起点//返回值:删剩下的孩子节点if (node == null){return null;}int result = key.compareTo(node.key);if (result < 0){node.left = doDelete(node.left,key,Aresult);return node;}if (result > 0){node.right = doDelete(node.right,key,Aresult);return node;}Aresult.add(node.value);if (node.left == null){return node.right;}if(node.right == null){return node.left;}BSTNode<T> s = node.right;while (s.left != null){s = s.left;}s.right = doDelete(node.right,s.key,new ArrayList<>());s.left = node.left;return s;}/*找比指定key小的所有节点的value值*/public List<Object> less(T key){ArrayList<Object> list = new ArrayList<>();BSTNode<T> p = root;LinkedList<BSTNode<T>> stack = new LinkedList<>();while (p != null || !stack.isEmpty()){if (p != null){stack.push(p);p = p.left;}else {BSTNode<T> pop = stack.pop();int result = key.compareTo( pop.key);if (result < 0 ){list.add(pop.value);} else {break;}p = pop.right;}}return list;}/*找比指定key小的所有节点的value值*/public List<Object> greater(T key){ArrayList<Object> list = new ArrayList<>();BSTNode<T> p = root;LinkedList<BSTNode<T>> stack = new LinkedList<>();while (p != null || !stack.isEmpty()){if (p != null){stack.push(p);p = p.left;}else {BSTNode<T> pop = stack.pop();int result = key.compareTo( pop.key);if (result > 0 ){list.add(pop.value);}p = pop.right;}}return list;}/*找比指定key小的所有节点的value值*/public List<Object> between(T key1,T key2){ArrayList<Object> list = new ArrayList<>();BSTNode<T> p = root;LinkedList<BSTNode<T>> stack = new LinkedList<>();while (p != null || !stack.isEmpty()){if (p != null){stack.push(p);p = p.left;}else {BSTNode<T> pop = stack.pop();int result1 = key1.compareTo( pop.key);int result2 = key2.compareTo( pop.key);if (result1 > 0 && result2 < 0){list.add(pop.value);}else if (result2 > 0){break;}p = pop.right;}}return list;}}
3.总结
怎么说呢,二叉搜索树对比前面的二叉树来说,难度确实是上了一个档次。但是,越学数据结构与算法你越会有这样一种感觉:他们的套路都大差不差!二叉搜索树是用链表来实现的,只要心中有图,多画画图,然后熟悉链表的一些操作,熟悉一些循环流程的判断,那么那些操作都能实现出来。如果实现不了,那就再多结合其他的数据结构来想一想。链表的操作主要就是看一些循环流程的控制。其余的没啥难的。对于数组,数组的一些操作要比链表难,因为数组太死了。
我之前的代码的注释比较多,因为刚接触,不熟悉,但现在代码中的注释并不多,那是因为一些操作都写了很多遍了。虽然不至于能默写下来,但是可以自己推导着写出来。思路有了,也练了几遍手,那么再遇见这个问题自己就能推导了。所以数据结构与算法学到后面主要就是学思路了。
相关文章:

数据结构与算法——17.二叉搜索树
这篇文章我们来看一下数据结构中的二叉搜索树。 目录 1.概述 2.二叉搜索树的实现 3.总结 1.概述 我们前面学到的数据结构,比如:动态数组、链表、队列、栈、堆,这些数据结构存储完数据后,我们要去查找某个数据,它的…...

rust所有权
一、堆和栈 栈和堆都是程序运行时使用的内存,但是它们的结构不同。 1.栈 栈,英文是stack。是内存的一段区域。 栈是后进先出形式的。就像薯片桶,先放进去的一片只能后拿出来。 栈上存储的数据大小必须是已知且固定的。也就是说如果一个变量…...
Win10电脑任务栏没有蓝牙图标的简单解决方法
Win10电脑任务栏没有蓝牙图标怎么办?在Win10电脑中,用户有时候会发现任务栏上没有蓝牙图标了,这样就无法通过蓝牙图标快速打开蓝牙服务了。下面小编给大家介绍最简单的解决方法,帮助大家找回任务栏上面的蓝牙图标吧。 问题原因 反…...

判断编译器类型、编译器版本、操作系统。
目录 1. 判断编译器类型: 2. 判断编译器版本: 3. 判断操作系统: 总结: 1. 判断编译器类型: 可以使用预定义的宏来判断编译器类型。例如,__GNUC__ 宏用于判断是否使用了GCC 编译器,_MSC_VER…...

百度实习一面(知识图谱部门)
百度面经(知识图谱部)一面 1.自我介绍 介绍完了,打开共享,对着简历一点一点问 2.ffmpeg在项目中是怎么使用的 回答了ffmpeg在项目中使用的命令,用来干了什么 3.为什么使用toml配置,了解过yml配置吗&am…...

Oracle 数据库查询优化
目录 1. Oracle 数据库查询优化(上百万级记录如何提高查询速度)2. Oracle SQL 性能优化 40 条 | 收藏了! 1. Oracle 数据库查询优化(上百万级记录如何提高查询速度) 对查询进行优化, 应尽量避免全表扫描, 首先应考虑在 where 及 order by 涉及的列上建立索引应尽量避免在 wher…...

时序预测 | MATLAB实现POA-CNN-GRU鹈鹕算法优化卷积门控循环单元时间序列预测
时序预测 | MATLAB实现POA-CNN-GRU鹈鹕算法优化卷积门控循环单元时间序列预测 目录 时序预测 | MATLAB实现POA-CNN-GRU鹈鹕算法优化卷积门控循环单元时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现POA-CNN-GRU鹈鹕算法优化卷积门控循环单元时间序…...

Java技术接单
今天给大家介绍一个阶段性(周期性)能获取一定收益的Java技术接单群,分享给大家!主要对搞Java的粉丝有帮助,因为可以赚点小钱,对Java技术的要求不高! 注意:首先进群不是免费的&#…...

多家企业发布基于大模型的AI产品,大模型应用落地哪家强?
https://m.mp.oeeee.com/a/BAAFRD000020230603805161.html “无产业不AI,无应用不AI。” 随着AI(人工智能)大模型技术落地,AI应用遍地开花。连日来,多家企业发布基于大模型的AI应用产品。身处“百模大战”时代&#x…...

如何在小程序中获取用户昵称、电话号,头像
一、如何获取昵称(获取微信昵称)以Taro框架为例 Taro框架中的组件Input的一个属性,type属性的值有一个nickname. 如果要拿到input的值,是要value结合onChange事件。 type"nickname" value{nickName} onChange{(value: …...
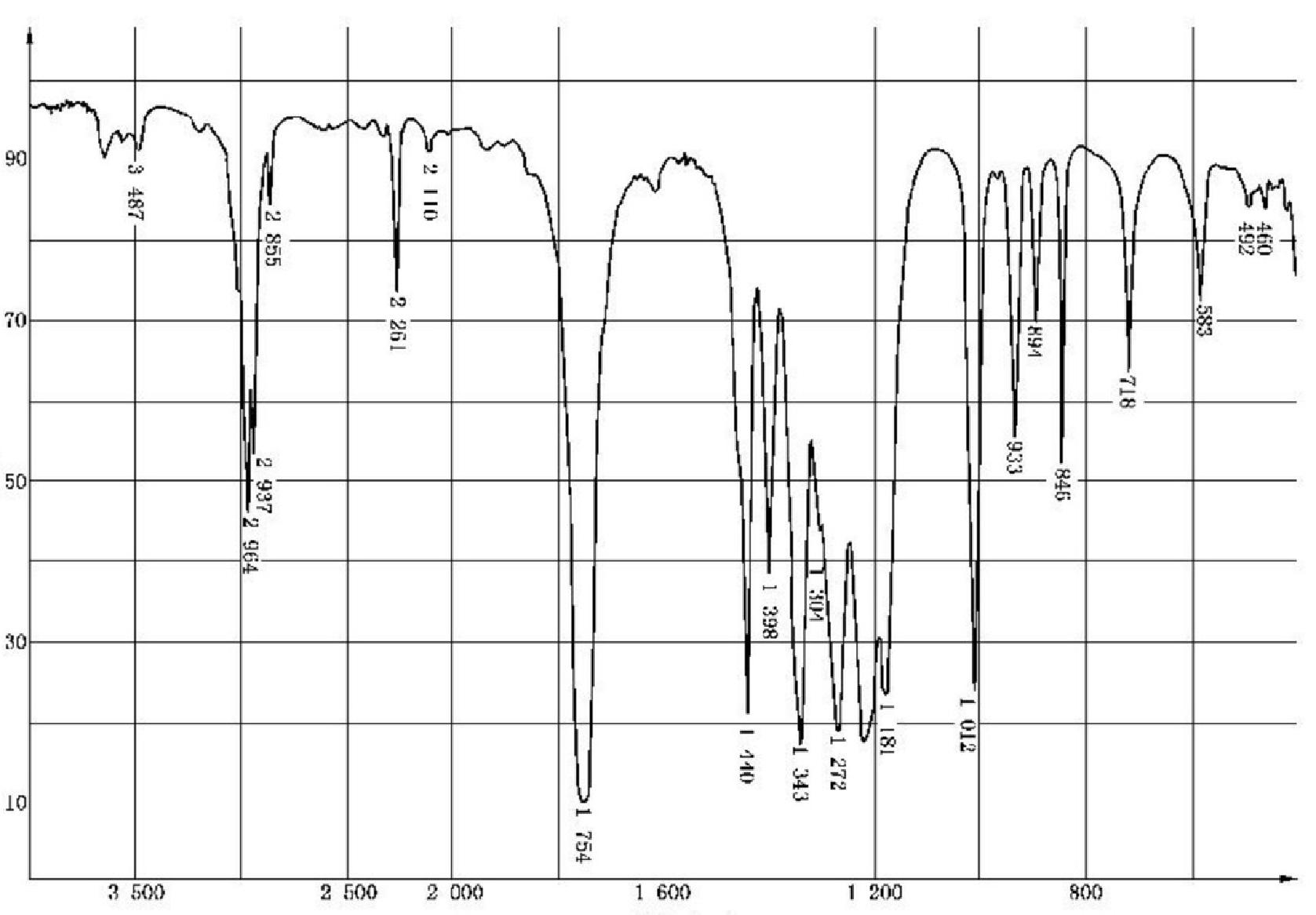
26606-2011 工业用氰乙酸甲酯 阅读笔记
声明 本文是学习GB-T 26606-2011 工业用氰乙酸甲酯. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了工业用氰乙酸甲酯的要求、试验方法、检验规则、标志、包装、运输、贮存和安全。 本标准适用于以氯乙酸、氰化钠、甲醇等为原料…...

微软开源 windows-drivers-rs, 用 Rust 开发 Windows 驱动程序
目录 1. 微软开源 windows-drivers-rs, 用 Rust 开发 Windows 驱动程序 1. 微软开源 windows-drivers-rs, 用 Rust 开发 Windows 驱动程序 Microsoft Azure 首席技术官兼著名 Windows 软件开发人员 Mark Russinovich 在社交平台上宣布, 启动了一个名为 windows-drivers-rs 的新…...

Java中判断字符串是否为合法数字
问题 最近遇到需要将String转BigDecimal的场景。 解决思路 利用NumberUtils.isCreatable判断是否为合法数字,然后,对字符串进行数字转换。注意:这里的NumberUtils类是org.apache.commons.lang3.math库里面的类。 Java if (NumberUtils.i…...

[LeetCode] Hard-2251. 花期内花的数目 - 二分查找/有序数组
Problem: 2251. 花期内花的数目 2251. 花期内花的数目 思路解题方法Code 思路 看题目应该是一道比较经典的差分,本来准备拿差分数组做的,后来搂了一眼题解,发现用二分的方法更简单 解题方法 此题有一种很简便的方法,第i个人到…...
 和 defineEmits())
VUE3父子组件传值defineProps() 和 defineEmits()
defineProps 和 defineEmits 都是只能在<script setup>中使用的编译器宏。他们不需要导入,且会随着 <script setup> 的处理过程一同被编译掉。 官网传送门 父组件向子组件传值 defineProps 是 Vue3 中一种新的组件数据传递方式,可以用于在…...

OmniPlan Pro 4 for Mac:引领项目管理的创新与高效
OmniPlan Pro 4是一款强大且高效的项目管理工具,专为Mac用户设计。它提供了一套综合性的解决方案,帮助用户在Mac上便捷地进行项目规划、追踪和管理。凭借其直观的界面,用户可以快速上手,并且能充分利用这款工具的各种功能。 规划…...

封装JDBC,实现简单ORM框架
本文将封装JDBC的操作,实现简单的ORM框架,提供3种风格的api来给用户使用(1.原生jdbcSqlBuilder;2.类似jpa和mp的;3.注解接口方法) 代码仓库:malred/IFullORM 1. 原生JDBCsql构建器 第一步&…...

监控与运维,主流it运维监控工具
IT监管和运行维护已成为企业经营的关键环节。本文将详细介绍IT监管和运行维护的必要性、主要功能和实施策略,帮助企业实现数据安全和高效运行。 IT监管和运行维护的必要性 确保企业数据安全 IT监控系统可以实时监控企业网络、服务器、存储等关键设备的运行情况&…...

基于Matlab实现全局优化算法
Matlab是一种非常强大的数学建模和计算工具,它提供了许多优化算法的实现。全局优化算法是一种能够找到全局最优解的优化算法,相对于局部优化算法来说,具有更强的全局搜索能力。在本文中,我们将介绍如何使用Matlab实现全局优化算法…...
)
Kafka 笔记 (Non-Root/Container)
目录 1. Kafka 笔记 (Non-Root/Container)1.1. 启动1.2. bitnami/kafka1.2.1. Non-Root Containers 1. Kafka 笔记 (Non-Root/Container) 1.1. 启动 Kafka 需要与 ZooKeeper 一起启动: Kafka with ZooKeeper Run the following commands in order to start all services in…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...
