[LeetCode] Hard-2251. 花期内花的数目 - 二分查找/有序数组
Problem: 2251. 花期内花的数目
2251. 花期内花的数目
- 思路
- 解题方法
- Code
思路
看题目应该是一道比较经典的差分,本来准备拿差分数组做的,后来搂了一眼题解,发现用二分的方法更简单
解题方法
此题有一种很简便的方法,第i个人到达时间为people[i],所以我们不难找到在这个时间之前花期已经开始的花的数量,即v1=start <= people[i];同理我们也可以找到在这之前花期已经结束的花的数量,即v2=end < people[i];由此不难得出花开数目即为v1-v2,而上述思路中找到在某个时间点之前花期开始或者结束的数目我们在有序数组starts和ends内用二分查找即可很好的解决这个问题,因此我们在处理好输入数据后还需要让starts和ends有序即可。
Code
class Solution {
public:vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {vector<int> ans;int n = flowers.size();vector<int> starts(n), ends(n);for(int i=0;i<n;i++){starts[i] = flowers[i][0];ends[i] = flowers[i][1];}sort(starts.begin(), starts.end());sort(ends.begin(), ends.end());int n2 = people.size();for(int i=0;i<n2;i++){int v1 = upper_bound(starts.begin(), starts.end(), people[i]) - starts.begin();int v2 = lower_bound(ends.begin(), ends.end(), people[i]) - ends.begin();ans.push_back(v1-v2);}return ans;}
};
相关文章:

[LeetCode] Hard-2251. 花期内花的数目 - 二分查找/有序数组
Problem: 2251. 花期内花的数目 2251. 花期内花的数目 思路解题方法Code 思路 看题目应该是一道比较经典的差分,本来准备拿差分数组做的,后来搂了一眼题解,发现用二分的方法更简单 解题方法 此题有一种很简便的方法,第i个人到…...
 和 defineEmits())
VUE3父子组件传值defineProps() 和 defineEmits()
defineProps 和 defineEmits 都是只能在<script setup>中使用的编译器宏。他们不需要导入,且会随着 <script setup> 的处理过程一同被编译掉。 官网传送门 父组件向子组件传值 defineProps 是 Vue3 中一种新的组件数据传递方式,可以用于在…...

OmniPlan Pro 4 for Mac:引领项目管理的创新与高效
OmniPlan Pro 4是一款强大且高效的项目管理工具,专为Mac用户设计。它提供了一套综合性的解决方案,帮助用户在Mac上便捷地进行项目规划、追踪和管理。凭借其直观的界面,用户可以快速上手,并且能充分利用这款工具的各种功能。 规划…...

封装JDBC,实现简单ORM框架
本文将封装JDBC的操作,实现简单的ORM框架,提供3种风格的api来给用户使用(1.原生jdbcSqlBuilder;2.类似jpa和mp的;3.注解接口方法) 代码仓库:malred/IFullORM 1. 原生JDBCsql构建器 第一步&…...

监控与运维,主流it运维监控工具
IT监管和运行维护已成为企业经营的关键环节。本文将详细介绍IT监管和运行维护的必要性、主要功能和实施策略,帮助企业实现数据安全和高效运行。 IT监管和运行维护的必要性 确保企业数据安全 IT监控系统可以实时监控企业网络、服务器、存储等关键设备的运行情况&…...

基于Matlab实现全局优化算法
Matlab是一种非常强大的数学建模和计算工具,它提供了许多优化算法的实现。全局优化算法是一种能够找到全局最优解的优化算法,相对于局部优化算法来说,具有更强的全局搜索能力。在本文中,我们将介绍如何使用Matlab实现全局优化算法…...
)
Kafka 笔记 (Non-Root/Container)
目录 1. Kafka 笔记 (Non-Root/Container)1.1. 启动1.2. bitnami/kafka1.2.1. Non-Root Containers 1. Kafka 笔记 (Non-Root/Container) 1.1. 启动 Kafka 需要与 ZooKeeper 一起启动: Kafka with ZooKeeper Run the following commands in order to start all services in…...

【Pytest】跳过执行之@pytest.mark.skip()详解
一、skip介绍及运用 在我们自动化测试过程中,经常会遇到功能阻塞、功能未实现、环境等一系列外部因素问题导致的一些用例执行不了,这时我们就可以用到跳过skip用例,如果我们注释掉或删除掉,后面还要进行恢复操作。 1、skip跳过成…...
防应用被LowMemoryKillerDaemon(LMKD)杀掉)
Android Framework 常见解决方案(22)防应用被LowMemoryKillerDaemon(LMKD)杀掉
1 原理说明 LMKD 借助 Linux 内核的 OOM(Out of Memory)机制来管理内存。当系统内存不足时,OOM 触发器会发送信号给LMKD,通知其进行内存管理。LMKD根据预先定义的策略和优先级,选择性地终止一些进程,以释放…...

Vue - 组件递归
目录 组件递归子组件父组件 组件递归 当要渲染一个目录时,因为可能有嵌套数据,并且组件的层级未知,可以使用组件递归来解决 注意点: 1,使用递归时必须提供 name,也就是通过组件的 name 递归自己。 2&am…...
微信小程序案例2-1:学生信息
文章目录 (二)准备图像素材(三)编写小程序页面结构 单击[确认] 清空页面结构文件index.wxml内容 修改页面配置文件index.json,不适用navigation-bar组件 删除全局配置文件app.json,删除渲染器配置&a…...
小程序如何设置余额充值
在小程序中设置余额充值是一种非常有效的方式,可以帮助商家吸引更多的会员并提高用户的消费频率。下面将介绍如何在小程序中设置余额充值并使用。 第一步:创建充值方案 在小程序管理员后台->营销管理->余额充值页面,添加充值方案。可…...

vue项目打包成H5apk中使用语音播放
利用浏览器语音播放api功能,在vue项目中调用api实现语音播报。 在mounted生命周期函数中获取浏览器的SpeechSynthesis API data() {return {speech: null,};},mounted() {if ("SpeechSynthesisUtterance" in window) {this.speech window.speechSynthesi…...
windows:批处理bat实例
文章目录 文件/文件夹管理实例批量更改文件名创建编号从0到9的10个文件自动循环运行某个程序显示批处理的完整路径信息将文件名更名为当前系统日期使用批处理命令自动接收用户输入的信息计算当前目录及子目录(中文件)所占硬盘空间自动删除当前目录及子目…...

websocket php教程
WebSocket 是 HTML5 提供的一种网络通讯协议,用于服务端与客户端实时数据传输。广泛用于浏览器与服务器的实时通讯,APP与服务器的实时通讯等场景。 相比传统HTTP协议请求响应式通讯,WebSocket协议可以做到实时的双向通讯,服务端可…...

【操作系统】调度算法的评价指标和三种调度算法
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 Redis 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 操作系统 一、调度算法的评价指标1.1 CPU利…...
CSS详细基础(三)复合选择器
前两章介绍了CSS中的基础属性,以及一些基础的选择器,本贴开始介绍复合选择器的内容~ 在 CSS 中,可以根据选择器的类型把选择器分为基础选择器和复合选择器,复合选择器是建立在基础选择器之上,对基本选择器进行组合形…...
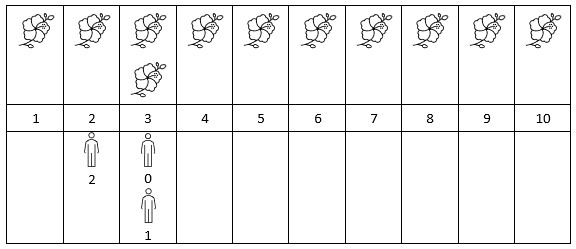
LeetCode【2251. 花期内花的数目】
给你一个下标从 0 开始的二维整数数组 flowers ,其中 flowers[i] [starti, endi] 表示第 i 朵花的 花期 从 starti 到 endi (都 包含)。同时给你一个下标从 0 开始大小为 n 的整数数组 people ,people[i] 是第 i 个人来看花的时间…...
:数据可视化(一))
大数据(九):数据可视化(一)
专栏介绍 结合自身经验和内部资料总结的Python教程,每天3-5章,最短1个月就能全方位的完成Python的学习并进行实战开发,学完了定能成为大佬!加油吧!卷起来! 全部文章请访问专栏:《Python全栈教程(0基础)》 再推荐一下最近热更的:《大厂测试高频面试题详解》 该专栏对…...
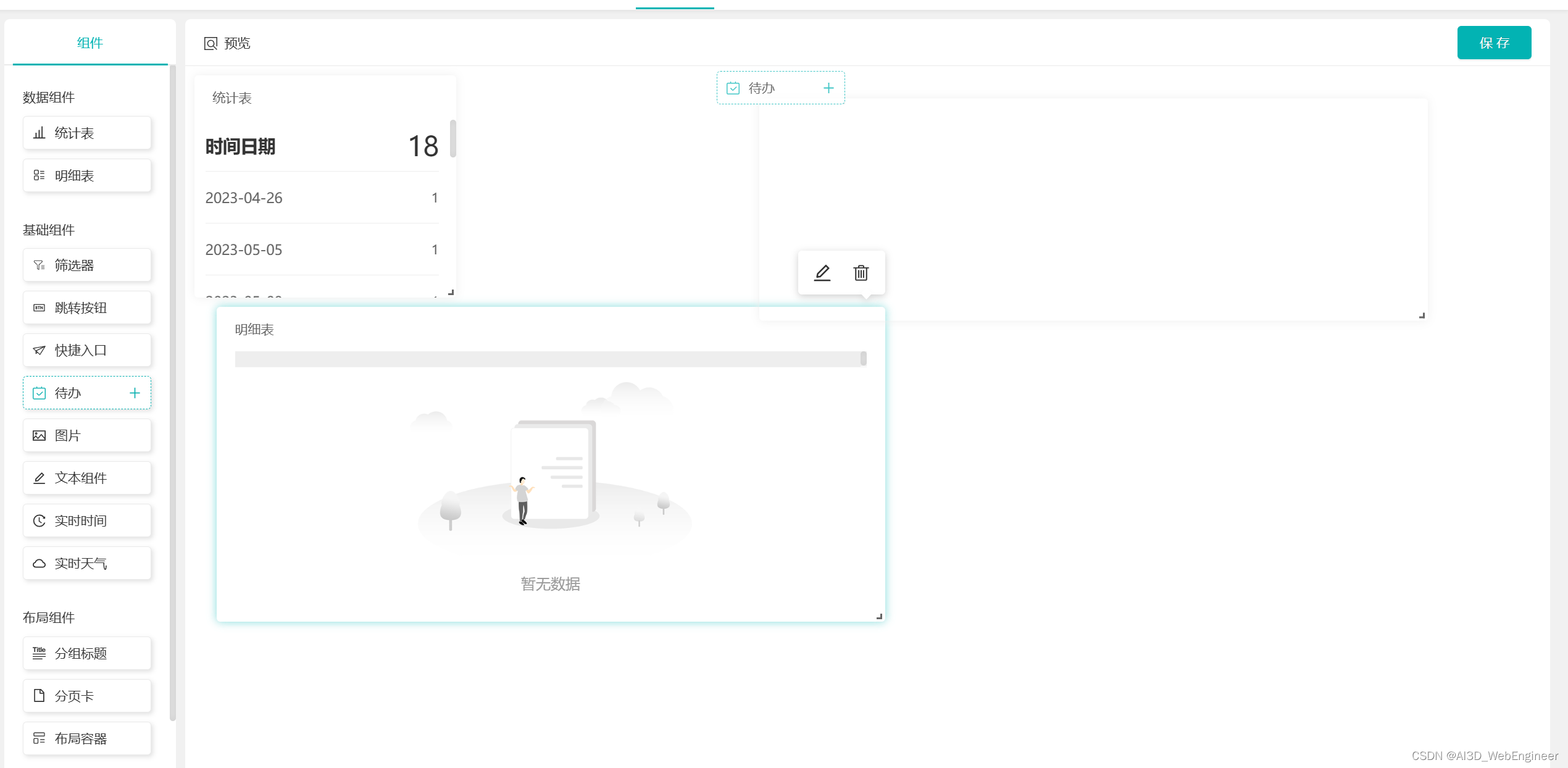
讲讲项目里的仪表盘编辑器(二)
应用场景 正常来说,编辑器应用场景应该包括: 编辑器-预览 编辑器 最终运行时 怎么去设计 上一篇推文,我们已经大概了解了编辑器场景。接下来,我们来看预览时的设计 编辑器-预览 点击预览按钮,执行以…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
